Symmetry

Symmetry in Mathematics: Complete Guide for Class 6 CBSE Maths

Introduction to Symmetry

Symmetry is a fundamental geometrical concept that appears throughout mathematics, nature, art, and architecture. When an object or shape can be divided into two identical halves that mirror each other, we say it possesses symmetry. This beautiful mathematical property helps us understand patterns, balance, and structure in the world around us.

The concept of symmetry is closely connected to mirror reflection. Imagine placing a mirror along a specific line in a shape if the reflected image matches the original perfectly, that line is called a line of symmetry or mirror line.

Real-World Examples of Symmetry

Symmetry surrounds us in everyday life:

• Nature: Butterflies, human faces, leaves, flowers
• Architecture: The Taj Mahal, modern buildings, bridges
• Objects: Vehicles, furniture, logos, letters

Line Symmetry (Reflection Symmetry)

What is Line Symmetry?

A shape has line symmetry when it can be folded along a line so that both halves match exactly. This imaginary fold line is called the axis of symmetry or line of symmetry. A figure may have one, multiple, or no lines of symmetry.

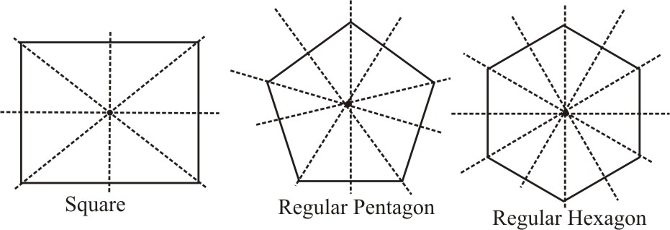
Lines of Symmetry in Regular Polygons

A regular polygon has all sides of equal length and all angles equal. The number of lines of symmetry in a regular polygon equals the number of its sides.

Polygon	Number of Sides	Lines of Symmetry
Equilateral Triangle	3	3
Square	4	4
Regular Pentagon	5	5
Regular Hexagon	6	6
Circle	∞	Infinite

Observations:

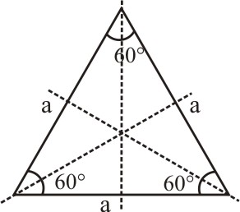
1. Equilateral Triangle: Has 3 lines of symmetry—each line passes through a vertex and the midpoint of the opposite side, making an angle of 60° with adjacent lines.
2. Square: Possesses 4 lines of symmetry—2 diagonal lines and 2 lines through the midpoints of opposite sides.
3. Rectangle: Unlike a square, has only 2 lines of symmetry—horizontal and vertical lines through the center (not the diagonals).
4. Circle: The most perfectly symmetrical figure with unlimited lines of symmetry passing through its center at any angle.

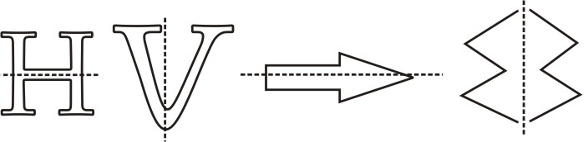
Lines of Symmetry in English Alphabets

Many English letters exhibit line symmetry:

• Vertical line of symmetry: A, H, I, M, O, T, U, V, W, X, Y
• Horizontal line of symmetry: B, C, D, E, H, I, O, X
• Both vertical and horizontal: H, I, O, X
• No line symmetry: F, G, J, K, L, N, P, Q, R, S, Z

Rotational Symmetry

Rotational Symmetry

An object has rotational symmetry if it looks exactly the same after being rotated by a certain angle about a fixed point called the center of rotation. The shape and size remain unchanged during this rotation.

Key Terms:

• Center of Rotation: The fixed point around which the object rotates
• Angle of Rotation: The angle through which the object is turned
• Order of Rotational Symmetry: The number of times a figure coincides with itself during one complete rotation (360°)

Calculating Order of Rotational Symmetry

The formula for the angle of rotation is:

Angle of Rotation = 360° ÷ Order of Rotational Symmetry

Examples of Rotational Symmetry

Shape	Order	Angle of Rotation
Equilateral Triangle	3	120°
Square	4	90°
Rectangle	2	180°
Regular Pentagon	5	72°
Regular Hexagon	6	60°
Circle	Infinite	Any angle

Note: Every object has rotational symmetry of order 1 (at 360°), but this is not considered significant.

Detailed Example: Equilateral Triangle

When an equilateral triangle rotates about its center:

• After 120° rotation: Same appearance (1st match)
• After 240° rotation: Same appearance (2nd match)
• After 360° rotation: Back to original position (3rd match)

Order of rotational symmetry = 3

Types of Symmetry in Mathematics

1. Reflection Symmetry (Line Symmetry)

A figure can be divided by a line so that each half is a mirror image of the other. This is the most common type taught at elementary levels.

Examples: Butterfly wings, the letter A, isosceles triangle

2. Rotational Symmetry

A figure looks identical after rotation by less than 360° about a central point.

Examples: Starfish, windmill blades, recycling symbol

3. Point Symmetry

Every part of the figure has a matching part at an equal distance from a central point but in the opposite direction. This is rotational symmetry of order 2 (180°).

Examples: The letter S, letter N, playing card designs

4. Translational Symmetry

A pattern repeats itself at regular intervals along a straight line (commonly seen in border designs and wallpapers).

Examples: Brick wall patterns, decorative borders, railway tracks

5. Glide Reflection Symmetry

A combination of translation and reflection, often seen in footprint patterns.

Examples: Footprints on sand, certain textile patterns

Symmetry in Nature

Nature is abundant with symmetrical patterns, which often serve functional purposes:

Radial Symmetry

Objects are arranged around a central point, like spokes on a wheel.

Examples:

• Flowers: Sunflowers, daisies, roses show radial symmetry with petals arranged around the center
• Sea Creatures: Starfish (5-fold symmetry), jellyfish, sea anemones
• Fruits: When you cut an apple or orange horizontally, you see radial symmetry

Bilateral Symmetry

One line divides the organism into two mirror-image halves (left and right).

Examples:

• Animals: Butterflies, birds, humans, most mammals
• Leaves: Many plant leaves show bilateral symmetry
• Insects: Beetles, dragonflies, bees

Spherical Symmetry

Symmetry in all directions from a central point.

Examples:

• Organisms: Some bacteria, pollen grains
• Natural Objects: Dewdrops, bubbles

Why Symmetry Exists in Nature

1. Efficiency: Symmetrical designs often require less genetic information to encode
2. Movement: Bilateral symmetry aids in directional movement
3. Mate Selection: Symmetry often signals health and genetic fitness
4. Resource Distribution: Radial symmetry allows equal access to resources from all directions

Symmetry in Architecture and Design

Historical Architecture

Symmetry has been a cornerstone of architectural design for millennia:

1. The Taj Mahal (India): Perfect bilateral symmetry with a central dome, four minarets, and gardens arranged symmetrically along a central axis
2. The Parthenon (Greece): Classical Greek architecture emphasizing symmetrical columns and proportions
3. Gothic Cathedrals: Notre-Dame and other cathedrals feature symmetrical facades with twin towers
4. The White House (USA): Neo-classical design with perfect bilateral symmetry

Modern Architecture and Design

Contemporary designers use symmetry strategically:

Advantages of Symmetrical Design:

• Creates visual balance and harmony
• Evokes feelings of stability and order
• Easier to plan and construct
• Universally appealing across cultures

Examples:

• Building Facades: Windows, doors, and decorative elements arranged symmetrically
• Interior Design: Furniture placement, room layouts
• Urban Planning: Gardens, parks with symmetrical pathways
• Logo Design: Many brands (Mercedes, Apple's old logo) use symmetry for recognition

Asymmetry in Modern Design

While symmetry conveys stability, designers sometimes deliberately break symmetry to:

• Create visual interest and dynamism
• Express modernity and innovation
• Guide eye movement and attention
• Reflect organic, natural forms

Group Theory and Symmetry Transformations

Introduction to Mathematical Symmetry

In advanced mathematics, symmetry is studied through group theory, a branch of abstract algebra. While this is beyond Class 6 curriculum, understanding the basics helps appreciate symmetry's deeper significance.

Symmetry Transformations

Four main types of transformations (operations) preserve a figure's shape and size:

1. Identity Transformation: The figure remains unchanged (like rotating 0° or 360°)
2. Reflection: Flipping the figure over a line (mirror line)
3. Rotation: Turning the figure around a fixed point
4. Translation: Sliding the figure without rotating or flipping

Symmetry Groups

Each geometric figure has a symmetry group—the set of all transformations that leave it unchanged.

Example: Square's Symmetry Group

• 4 rotations: 0°, 90°, 180°, 270°
• 4 reflections: 2 through midpoints, 2 through diagonals
• Total: 8 symmetry operations

This systematic study helps:

• Classify crystals in chemistry
• Understand molecular structures
• Solve complex geometric problems
• Analyze patterns in physics

Symmetry vs. Asymmetry in Art

The Role of Symmetry in Art

Symmetrical Art:

• Conveys harmony, balance, and formality
• Common in religious art, traditional portraits
• Creates a sense of calm and order
• Examples: Leonardo da Vinci's "Vitruvian Man", Islamic geometric patterns

Techniques Using Symmetry:

1. Mandala Art: Circular designs with radial symmetry used in meditation
2. Kaleidoscope Patterns: Multiple reflections creating complex symmetrical designs
3. Renaissance Paintings: Symmetrical composition for religious subjects
4. Architecture Drawings: Symmetric floor plans and elevations

Asymmetry in Modern Art

Asymmetrical Art:

• Creates tension, movement, and visual interest
• More common in modern and contemporary art
• Directs viewer's attention deliberately
• Examples: Abstract expressionism, modern photography compositions

The Rule of Thirds: Photographers and artists often use asymmetric compositions where subjects are placed off-center at imaginary gridline intersections.

Combining Both Approaches

Great art often balances symmetry and asymmetry:

• Overall symmetry with asymmetrical details creates interest without chaos
• Breaking symmetry strategically draws attention to focal points
• Natural scenes often blend both (symmetric tree with asymmetric branch arrangement)

Key Formulas and Concepts

Concept	Formula/Rule	Explanation
Lines of Symmetry (Regular Polygon)	Number of lines = Number of sides	Each regular polygon has symmetry lines equal to its side count
Angle of Rotation	θ = 360° ÷ n	Where n = order of rotational symmetry
Order of Rotational Symmetry	n = 360° ÷ θ	Where θ = smallest angle giving same appearance
Complete Rotation	360° or 2π radians	Full turn returns to original position
Circle's Lines of Symmetry	Infinite	Any diameter is a line of symmetry

Solved Examples

Example 1: Finding Lines of Symmetry

Question: How many lines of symmetry does a rectangle have?

Solution: A rectangle has 2 lines of symmetry:

1. Horizontal line through the center (parallel to longer sides)
2. Vertical line through the center (parallel to shorter sides)

Note: The diagonals of a rectangle are NOT lines of symmetry because when folded along a diagonal, the halves don't match perfectly.

Example 2: Paper Folding

Question: A paper is folded in half and two holes are punched. When unfolded, where will the holes appear?

Solution: The holes will appear symmetrically on both halves with the fold line as the axis of symmetry. If you punched holes on the left side, identical holes will appear at corresponding positions on the right side, equidistant from the fold line.

Example 3: Rotational Symmetry Order

Question: Find the order of rotational symmetry for a regular hexagon.

Solution: A regular hexagon has 6 sides, so:

• Order of rotational symmetry = 6
• Angle of rotation = 360° ÷ 6 = 60°

The hexagon looks identical after rotations of 60°, 120°, 180°, 240°, 300°, and 360°.

Practice Questions

Subjective Questions

1. Identify all lines of symmetry in the following letters: H, N, B, I, M, Z
2. Draw the reflection of the given holes across the line of symmetry for:
   • A square with one hole in the top-left corner
   • A triangle with holes along one side
   • A circle with an off-center hole
3. Which of these alphabets have line symmetry: S, O, H, N, B, I, M, Z?
4. Find the order of rotational symmetry for:
   • A cross shape (+)
   • A five-pointed star
   • A rectangular cross
5. Calculate the angle of rotation and order of rotational symmetry for:
   • Rectangle: Order = 2, Angle = 180°
   • Rhombus: Order = 2, Angle = 180°
   • Semi-circle: Order = 1 (no rotational symmetry except 360°)

Important Points to Remember

• Line symmetry requires a fold line where both halves match exactly
• Regular polygons always have lines of symmetry equal to their number of sides
• Rotational symmetry means the figure looks the same after rotating less than 360°
• The circle is the most symmetrical shape with infinite lines of symmetry
• Rectangles have 2 lines of symmetry, but squares have 4
• Not all shapes with rotational symmetry have line symmetry (example: letter S)
• Order of rotational symmetry = 360° ÷ (smallest rotation angle)
• Every object has at least order 1 rotational symmetry (360° rotation)

Conclusion

Symmetry is a fascinating concept that bridges mathematics, art, nature, and design. Understanding line symmetry and rotational symmetry helps students recognize patterns and structure in the world around them. From the perfectly symmetrical circle to the balanced architecture of historical monuments, symmetry demonstrates the beauty and order inherent in mathematical principles.

As you continue studying geometry, you'll discover that symmetry isn't just about aesthetics it's a powerful tool for solving problems, classifying shapes, and understanding the fundamental principles governing our universe.