circle

Equations of the Circle in Various Forms

1. The simplest equation of the circle: x² + y² = r² where centre is (0, 0) and radius r.
2. Circle with centre (a, b) and radius r: (x - a)² + (y - b)² = r²
3. General equation of a circle: x² + y² + 2gx + 2fy + c = 0 with centre (-g, -f) and radius = √(g² + f² - c)
4. Equation with diameter endpoints P(x₁, y₁) and Q(x₂, y₂): (x - x₁)(x - x₂) + (y - y₁)(y - y₂) = 0

Parametric Equation of a Circle

The equations x = a cos θ, y = a sin θ are called parametric equations of the circle x² + y² = a² and θ is called a parameter. The point (a cos θ, a sin θ) is also referred to as point θ. The parametric coordinates of any point on the circle (x - h)² + (y - k)² = a² are given by:
(h + a cos θ, k + a sin θ) with 0 ≤ θ < 2π

Illustration 1: The equation of the circle whose centre is (1, 2) and which passes through the point (4, 6) is

(A) x² + y² + 2x + 4y = 20

(B) x² + y² - 2x - 4y = 20

(C) x² + y² - 2x - 4y + 20 = 0

(D) none of these

Solution: (B) Distance from the centre to a point through which circle passes gives us the radius.

Therefore the radius of the circle is: r = √[(4-1)² + (6-2)²] = √25 = 5

Hence the equation of the circle is: (x-1)² + (y-2)² = 25 ⟹ x² + y² - 2x - 4y = 20

The Position of a point with respect to a Circle

The point P(x₁, y₁) lies outside, on, or inside a circle S ≡ x² + y² + 2gx + 2fy + c = 0, according as: S₁ ≡ x₁² + y₁² + 2gx₁ + 2fy₁ + c >, =, or < 0

Equations of Tangents and Normals

1. Equation of the tangent at A(x₁, y₁): xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
2. Condition for line y = mx + c to be tangent to x² + y² = a²: c² = a²(1 + m²)
   Point of contact: (-a²m/c, a²/c)
   y = mx ± a√(1 + m²) is always a tangent to the circle x² + y² = a² whatever be the value of m.
3. Joint equation of pair of tangents from A(x₁, y₁): T² = SS₁
4. Equation of the normal at (x₁, y₁): (x - x₁)/(x₁ + g) = (y - y₁)/(y₁ + f)

Additional Important Formulas

• Equation of chord with given mid-point (x₁, y₁): T = S₁
• Length of tangent from external point (x₁, y₁): √S₁

Chord of Contact

From a point P(x₁, y₁) two tangents PA and PB can be drawn to the circle. The chord AB joining the points of contact A and B of the tangents from P is called the chord of contact of P(x₁, y₁) with respect to the circle. Its equation is given by: T = 0

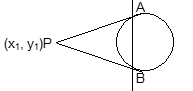
Illustration 2:  The line y = x + a√2 touches the circles x² + y² = a² at the point

(A) (-a/√2, a/√2)

(B) (a/√2, -a/√2)

(C) (-a/√2, -a/√2)

(D) (a/√2, a/√2)

Solution: (A) Let (α, β) be the point where the line touches the circle.

Equation of the tangent to the circle at (α, β) is: xα + yβ - a² = 0

Comparing coefficients: α/1 = β/1 = -a²/(-a√2)

Therefore: α = -a/√2, β = a/√2 Hence point of contact is (-a/√2, a/√2)

Exercise 1:

(i) If the equations of the two diameters of a circle are x + y = 6 and x + 2y = 4 and the radius of the circle is 10, then the equation of the circle is

(A) x² + y² - 16x + 4y - 32 = 0

(B) x² + y² + 16x - 4y - 32 = 0

(C) 3(x² + y²) - 16x + 4y - 32 = 0

(D) none of these

(ii) The circle x² + y² - 4x - 8y + 16 = 0 rolls up the tangent to it at (2 + √3, 3) by 2 units. Assuming the x-axis as horizontal, the equation of the circle in the new position is given by

(A) x² + y² - 4x - 8y + 14 = 0

(B) x² + y² - 4x - 8y + 16 = 0

(C) x² + y² - 6x - 8y + 24 + 8√3 = 0

(D) none of these

Equation of the Radical Axis

In general S - S' = 0 represents the equation of the Radical Axis to the two circles
2x(g - g') + 2y(f - f') + c - c' = 0

If S = 0 and S' = 0 intersect in real and distinct points then S - S' = 0 is the equation of the common chord of the two circles.

Coaxial Circles

A system of circles is said to be coaxial if each pair of circles of the system has the same radical axis.

• If the equation of a circle is S = 0 and the equation of a line P = 0, then S + λP = 0 represents a system of co-axial circles with P = 0 as their radical axis.
• Similarly, if S₁ = 0 and S₂ = 0 are two circles then S₁ + λS₂ = 0 is a system of co-axial circles.

Illustration 3: The equation of a circle which is coaxial with the circles 2x² + 2y² - 2x + 6y - 3 = 0 and x² + y² + 4x + 2y + 1 = 0 (It is given that the centre of the circle to be determined lies on the radical axis of these circles) is

(A) x² + y² + 6x + 10y - 1 = 0

(B) 2(x² + y²) + 6x + 10y - 1 = 0

(C) 4(x² + y²) + 6x + 10y - 1 = 0

(D) none of these

Solution: (C) Equation of the given circles are:

S₁ = x² + y² - x + 3y - 3/2 = 0 ... (1)

S₂ = x² + y² + 4x + 2y + 1 = 0 ... (2)

The radical axis of circles (1) and (2) is:

S₁ - S₂ = 0 or -5x + y - 5/2 = 0 Or, 10x - 2y + 5 = 0 ... (3)

Required circle will have the equation of the form:

x² + y² + 4x + 2y + 1 + k(10x - 2y + 5) = 0

or, x² + y² + 2(2 + 5k)x + 2(1 - k)y + (1 + 5k) = 0 ... (4)

Its centre is (-2 - 5k, k - 1). From question, it lies on line (3)

10(-2 - 5k) - 2(k - 1) + 5 = 0 or -52k - 13 = 0 k = -1/4

Putting the value of k in (4), we get: 4(x² + y²) + 6x + 10y - 1 = 0

Orthogonal Circles

The two circles are said to intersect orthogonally if the angle of intersection of the circles i.e., the angle between their tangents at the point of intersection is 90°.

The condition for the two circles S = 0 and S₁ = 0 to cut each other orthogonally is: 2gg₁ + 2ff₁ = c + c₁

Illustration 4: The equation to the circle which intersect the circles x² + y² - 6y + 1 = 0 and x² + y² - 4y + 1 = 0 orthogonally and touch the line 3x + 4y + 5 = 0 can be given by

(A) 4(x² + y²) + 15x - 4 = 0

(B) 4(x² + y²) + 15x + 4 = 0

(C) x² + y² - 1 = 0

(D) x² + y² + 1 = 0

Solution: (C) Let the equation of the circle which cuts the given two circles orthogonally be: x² + y² + 2gx + 2fy + c = 0 ... (1)

According to the condition, we get: 2g·0 + 2f(-3) = c + 1 ⟹ -6f = c + 1 2g·0 + 2f(-2) = c + 1 ⟹ -4f = c + 1

Solving them, f = 0 and c = -1 Now, (1) becomes: x² + y² + 2gx - 1 = 0 ... (2)

Centre is (-g, 0) and radius is √(g² + 1)

Now, (2) touches the line 3x + 4y + 5 = 0 if: |3(-g) + 4·0 + 5|/√(3² + 4²) = √(g² + 1)

Solving: 8g² + 15g = 0 ⟹ g = 0, -15/8

From (2), equation of circle is: x² + y² - 1 = 0 or 4(x² + y²) - 15x - 4 = 0

Exercise 2:

(i) The circle on the chord x cos α + y sin α - p = 0 of the circle x² + y² = a² as diameter is

(a) x² + y² - a² - 2px cos α + y sin α - p = 0

(b) x² + y² - a² - 2p(x cos α + y sin α + p) = 0

(c) x² + y² - a² - 2p(x cos α + y sin α - p) = 0

(d) none of these

(ii) Tangents PQ and PR are drawn to the circle x² + y² = a² from the point P(x₁, y₁). The equation of the circumcircle of ΔPQR is

(a) x² + y² - xx₁ - yy₁ = 0

(b) x² + y² + xx₁ + yy₁ = 0

(c) 2(x² + y²) - xx₁ - yy₁ = 0

(d) none of these

(iii) The radical axis of the circles x² + y² + 2gx + 2fy + c = 0 and 2x² + 2y² + 3x + 8y + 2c = 0 touches the circle x² + y² + 2x - 2y + 1 = 0. If f ≠ 2, then the value of g is

(a) 3/4

(b) 1/2

(c) 2

(d) 4/3

External and Internal Contacts of Circles

External Contact: If two circles with centres C₁(x₁, y₁) and C₂(x₂, y₂) and radii r₁ and r₂ respectively, touch each other externally, then:
C₁C₂ = r₁ + r₂

Coordinates of the point of contact are:

A = ((r₂x₁ + r₁x₂)/(r₁ + r₂), (r₂y₁ + r₁y₂)/(r₁ + r₂))

Internal Contact: The circles touch each other internally if:

C₁C₂ = |r₁ - r₂|

Coordinates of the point of contact are:

T = ((r₁x₂ - r₂x₁)/(r₁ - r₂), (r₁y₂ - r₂y₁)/(r₁ - r₂))

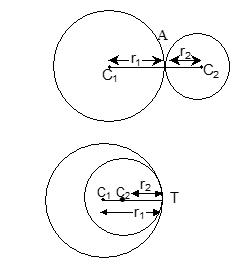
Common Tangents of two circles

1. Direct common tangents: Meet on the line of centres and divide it externally in the ratio of the radii.
2. Transverse common tangents: Also meet on the line of centres and divide it internally in the ratio of the radii.

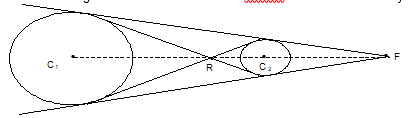
Illustration 5: The circle x² + y² + 2ax + c² = 0 and x² + y² + 2by + c² = 0 touch each other if

(A) 1/a² + 1/b² = 1/c²

(B) 1/a² - 1/b² = 1/c²

(C) a² + b² = c²

(D) none of these

Solution: (A) Centre A ≡ (-a, 0), B ≡ (0, -b) r₁ = √(a² - c²), r₂ = √(b² - c²)

The two circles will touch each other if AB² = (r₁ ± r₂)² or a² + b² = r₁² + r₂² ± 2r₁r₂ or

a² + b² = a² - c² + b² - c² ± 2√((a² - c²)(b² - c²)) or

2c² = ±2√((a² - c²)(b² - c²)) or c⁴ = (a² - c²)(b² - c²) or

c²b² + a²c² = a²b² or 1/a² + 1/b² = 1/c²

Exercise 3:

(i) The circles x² + y² + 24ux + 2vy = 0 and x² + y² + 2u₁x + 2v₁y = 0 touch each other if

(a) uv₁ + u₁v = 0

(b) uv₁ - u₁v = 0

(c) uv₁ + u₁v = 1

(d) uv₁ + u₁v = 5

(ii) The tangent to the circle x² + y² = 5 at the point (1, k) also touches the circle x² + y² - 8x + 6y + 20 = 0 if k is equal to

(a) 1

(b) 4

(c) 2

(d) none of these

(iii) A circle of radius 2 lies in first quadrant and touches both the coordinate axis. The equation of the circle with centre at (6, 5) and touching the above circle externally is

(a) x² + y² + 12x + 10y + 52 = 0

(b) x² + y² - 12x - 10y + 52 = 0

(c) x² + y² - 12x + 10y + 52 = 0

(d) none of these

Pole and Polar

If from a point P any straight line is drawn to meet the circle in Q and R and if tangents to the circle at Q and R meet in T. Then the locus of T is called the polar of P with respect to the circle.

The point P is called the pole of the polar.

Equation of polar of the point P(x₁, y₁) with respect to the circle x² + y² + 2gx + 2fy + c = 0 is:

xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0

Coordinates of pole of the line lx + my + n = 0 with respect to the circle x² + y² = a² are:

(-a²l/n, -a²m/n)

Some Properties of Pole and Polar

1. If the polar of a point P with respect to a circle passes through Q then the polar of Q with respect to the circle will pass through P. Points P and Q are called the conjugate points.
2. If the pole of a line with respect to the circle lies on another line, then the pole of the other line with respect to the same circle will lie on the first line. The straight lines as described above are called the conjugate lines.

Illustration 6: The pole of the line 3x + 5y + 17 = 0 with respect to the circle x² + y² + 4x + 6y + 9 = 0 is

(A) (1, -2)

(B) (1, 2)

(C) (1, 1)

(D) (2, 1)

Solution: (B)

Given circle x² + y² + 4x + 6y + 9 = 0 ...(1)

and the given line 3x + 5y + 17 = 0 ...(2)

Let P(α, β) be the pole of the line (2) with respect to circle (1)

Now equation of polar of point P(α, β) with respect to circle (1) is

xα + yβ + 2(x + α) + 3(y + β) + 9 = 0

or (α + 2)x + (β + 3)y + 2α + 3β + 9 = 0 ...(3)

Now lines (2) and (3) are same, therefore,

(α + 2)/3 = (β + 3)/5 = (2α + 3β + 9)/17

From (i) and (ii), we get

5α + 10 = 3β + 9 or 5α - 3β = -1 ...(4)

From (i) and (iii), we get

17α + 34 = 6α + 9β + 27 or 11α - 9β = -7 ...(5)

Solving (4) and (5), we get α = 1, β = 2

Hence required pole is (1, 2).

Answer to Exercises

Exercise 1:

(i) B (ii) D

Exercise 2:

(i) C (ii) A (iii) A

Exercise 3:

(i) B (ii) C (iii) B

Formulae and Concepts at a Glance

1. The simplest equation of the circle is x² + y² = r² whose centre is (0, 0) and radius r.
2. The equation (x - a)² + (y - b)² = r² represents a circle with centre (a, b) and radius r.
3. The equation x² + y² + 2gx + 2fy + c = 0 is the general equation of a circle with centre (-g, -f) and radius √(g² + f² - c).
4. Equation of the circle with points P(x₁, y₁) and Q(x₂, y₂) as extremities of a diameter is (x - x₁)(x - x₂) + (y - y₁)(y - y₂) = 0.
5. The point P(x₁, y₁) lies outside, on, or inside a circle S ≡ x² + y² + 2gx + 2fy + c = 0, according as S₁ ≡ x₁² + y₁² + 2gx₁ + 2fy₁ + c > = or < 0.
6. Equation of the tangent to the circle x² + y² + 2gx + 2fy + c = 0 at A(x₁, y₁) is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0.
7. The condition that the straight line y = mx + c is a tangent to the circle x² + y² = a² is c² = a²(1 + m²) and the point of contact is (-a²m/c, a²/c) i.e. y = mx ± a√(1 + m²) is always a tangent to the circle x² + y² = a² whatever be the value of m.
8. The joint equation of a pair of tangents drawn from the point A(x₁, y₁) to the circle x² + y² + 2gx + 2fy + c = 0 is T² = SS₁.
9. The equation of the normal to the circle x² + y² + 2gx + 2fy + c = 0 at any point (x₁, y₁) lying on the circle is (x - x₁)/(x₁ + g) = (y - y₁)/(y₁ + f).
10. The equation of the chord of the circle S ≡ 0, with mid point (x₁, y₁) is T = S₁.
11. The length of the tangent drawn from a point (x₁, y₁) outside the circle S ≡ 0, is √S₁.
12. Locus of point of intersection of two mutually perpendicular tangents to the circle is called director circle. For circle x² + y² = a², equation of director circle is given by x² + y² = 2a².
13. S - S' = 0 represents the equation of the Radical Axis to the two circles. i.e. 2x(g - g') + 2y(f - f') + c - c' = 0
14. If S ≡ x² + y² + 2gx + 2fy + c = 0 and S' ≡ x² + y² + 2g'x + 2f'y + c' = 0 are two intersecting circles, then S + λS' = 0, λ ≠ -1, is the equation of the family of circles passing through the points of intersection of S = 0 and S' = 0.
15. Condition for two circles S = 0 and S₁ = 0 to cut each other orthogonally is 2gg₁ + 2ff₁ = c + c₁.

Solved Examples

Q1. Four distinct points (2K, 3K), (1,0), (0,1) and (0,0) lie on a circle when

(A) all are integral values of K

(B) 0 < K < 1

(C) K < 0

(D) For two values of K

Sol. (D). The equation of the circle passing through the point (1, 0), (0, 1) and (0, 0) is

x² + y² – x – y = 0, which passes through (2k, 3k), if

4k² + 9k² – 2k – 3k = 0 ⇒ k = 0, k = 5/13.

Q2. The equation of the image of the circle x² + y² + 16x – 24y + 183 = 0 by the line mirror 4x + 7y + 13 = 0 is

(A) x² + y² + 32x – 4y + 235 = 0

(B) x² + y² + 32x + 4y – 235 = 0

(C) x² + y² + 32x – 4y – 235 = 0

(D) x² + y² + 32x + 4y + 235 = 0

Sol. (D). Image of the centre = (–16, –2) So equation of required circle is (x + 16)² + (y + 2)² = 5²

Q3. If the circles x² + y² + 2x + 2ky + 6 = 0 and x² + y² + 2ky + k = 0 intersect orthogonally, then k is

(A) 2 or –3/2

(B) –2 or –3/2

(C) 2 or 3/2

(D) –2 or 3/2

Sol. (A). Apply 2gg₁ + 2ff₁ = c₁ + c₂ ⇒ 2(0) + 2kk = 6 + k or 2k² – k – 6 = 0 ⇒ k = 2, –3/2

Q4. Equation of the circle whose radius is 5 and which touches externally the circle x² + y² – 2x – 4y – 20 = 0 at the point (5, 5) is

(A) (x – 9)² + (y – 6)² = 5²

(B) (x – 9)² + (y – 8)² = 5²

(C) (x – 7)² + (y – 3)² = 5²

(D) none of these

Sol. (B). If (h, k) be the centre then (5, 5) is the mid–point of (h, k) and (1, 2) because the radii of both the circles are 5 each ⇒ h = 9, k = 8.

Q5. If the circles (x – a)² + (y – b)² = c² and (x – b)² + (y – a)² = c² touch each other then

(A) a = b ± 2c

(B) a = b ± c√2

(C) a = b ± c

(D) none of these

Sol. (B). The circles will touch each other ⇒ c₁c₂ = r₁ + r₂ ⇒ a = b ± c√2

Q6. The length of the common chord of the circles x² + y² + 2x + 3y + 1 = 0 and x² + y² + 4x + 3y + 2 = 0, is

(A) 9/2

(B) 2√2

(C) 3√2

(D) √3/2

Sol. (B). Equation of common chord is 2x + 1 = 0 ⇒ x = –1/2

This cuts the circle at points (-1/2)² + y² + 2(-1/2) + 3y + 1 = 0

⇒ 1/4 + y² – 1 + 3y + 1 = 0 ⇒ 4y² + 12y + 1 = 0 ⇒ y = (-12 ± 8√2)/8 = (-3 ± 2√2)/2

∴ length = 2√2.

Q7. The number of common tangents that can be drawn to the circle x² + y² – 4x – 6y – 3 = 0 and x² + y² + 2x + 2y + 1 = 0 is

(A) 1

(B) 2

(C) 3

(D) 4

Sol. (C). The two circles are x² + y² – 4x – 6y – 3 = 0 and x² + y² + 2x + 2y + 1 = 0

Centre: C₁ ≡ (2, 3), C₂ ≡ (–1, –1); radii: r₁ = 4, r₂ = 1

We have, C₁C₂ = 5 = r₁ + r₂, therefore there are 3 common tangents to the given circles.

Q8. Tangents to the circle x² + y² = a² cut the circle x² + y² = 2a² at P and Q. The tangents at P and Q to the circle x² + y² = 2a² intersect at angle θ, then θ is equal to

(A) π/4

(B) π/6

(C) π/3

(D) π/2

Sol. (D). Equation of tangent at any point (a cos α, a sin α) is x cos α + y sin α = a ...(1)

Let the point of intersection of the tangents at P and Q be (h, k). If the tangents at P and Q intersect at right angles, then locus of (h, k) will be director circle of x² + y² = 2a² i.e. x² + y² = 4a². PQ is chord of contact of the circle x² + y² = 2a² w.r.t. the point (h, k) i.e. equation of PQ is hx + ky = 2a² ...(2)

(1) and (2) are same equation ⇒ cos α/h = sin α/k = a/(2a²) = 1/(2a)

cos²α + sin²α = 1 ⇒ h² + k² = 4a²

∴ locus of (h,k) is x² + y² = 4a² which is director circle to x² + y² = 2a²

Q9. If tangent at (1, 2) to the circle x² + y² = 5 intersects the circle x² + y² = 9 at A and B and tangents at A and B to the second circle meet at point C, then the coordinates of C are

(A) (-1/5, 9/5)

(B) (-1/5, 2/5)

(C) (9/5, 8/5)

(D) (9/5, 18/5)

Sol. (D). The tangent at (1, 2) is given by x + 2y – 5 = 0

Let point C be (h, k). Then this tangent will be chord of contact of this point w.r.t. IInd circle so, equation will be xh + yk – 9 = 0, both are same lines so

h/1 = k/2 = 9/5 ⇒ (h,k) = (9/5, 18/5)

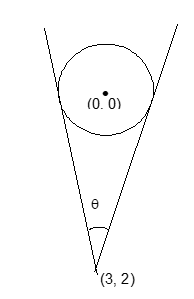
Q10. The angle between the pair of tangents from the point A(3, 2) to the circle x² + y² = 4 is given by

(A) tan⁻¹(2/5)

(B) tan⁻¹(5/2)

(C) tan⁻¹(12/5)

(D) tan⁻¹(3/5)

Sol. (C). The equation of the pair of tangents from (3, 2) is given by

T² = SS₁

⇒ (3x + 2y – 4)² = (x² + y² – 4)(9 + 4 – 4)

i.e., 9x² + 4y² + 16 + 12xy – 16y – 24x = 9x² + 9y² – 36

⇒ 5y² + 24x + 16y – 12xy – 52 = 0

Here a = 0, b = 5, h = –6.

Hence angle θ between the tangents is given by

tan θ/2 = 2√(h² - ab)/(a + b) or tan θ = 2 × 6/5

or tan θ = 12/5 ⇒ θ = tan⁻¹(12/5).

Hence the angle between the pair of tangents is tan⁻¹(12/5).

Assignment

Q1. The radius of the circle inscribed in the triangle formed by x = 0, y = 0, 4x + 3y – 24 = 0 is
(A) 12

(B) 2

(C) 2√2

(D) 6

Q2. The equation of radical axis of the circles 2x² + 2y² – 7x = 0 and x² + y² – 4y – 7 = 0 is

(A) 7x + 8y + 14 = 0

(B) 7x – 8y + 14 = 0

(C) 7x – 8y – 14 = 0

(D) none of these

Q3. AB is a diameter of a circle and c is any point on the circumference of the circle. Then

(A) the area of △ABC is maximum when it is isosceles

(B) the area of △ABC is minimum when it is isosceles

(C) the perimeter of △ABC is maximum when it is isosceles

(D) none of these

Q4. The circle described on the line joining the points (0, 1), (a, b) as diameter cuts the x–axis at points whose abscissae are roots of the equation

A) x² + ax + b = 0

(B) x² – ax + b = 0

(C) x² + ax – b = 0

(D) x² – ax – b = 0

Q5. The circles x² + y² + 6x + 6y = 0 and x² + y² – 12x – 12y = 0

(A) touch each other internally

(B) touch each other externally

(C) intersect in two points

(D) cut orthogonally

Q6. The equation of the normal to the circle x² + y² = 2x, which is parallel to the line x + 2y = 3 is

(A) 15(x² + y²) – 94x + 18y + 55 = 0

(B) 5(x² + y²) – 94x + 18y + 55 = 0

(C) x² + y² – 94x + 18y + 55 = 0

(D) x² + y² – 6x + 3y + 3 = 0

Q7. The circle x² + y² – 6x – 4y + k = 0 bisects the circumference of the circle x² + y² – 8x – 6y + 23 = 0, for k is equal to

(A) 7

(B) 6

(C) 9

(D) 5

Q8. C₁ and C₂ are the centres of two circles whose radii are r₁ and r₂. The two circles touch each other internally iff

(A) |C₁C₂| = r₁ + r₂

(B) |C₁C₂| = |r₁ – r₂|

(C) |C₁C₂| = r₁ – r₂

(D) |C₁C₂| = r₂ – r₁

Q9. Circumcentre of the triangle, whose vertices are (0, 0), (6, 0) and (0, 4) is

A) (2, 0)

(B) (3, 0)

(C) (0, 3)

(D) (3, 2)

Q10. The locus of the point of intersection of the lines x cos α + y sin α = 0 and x sin α – y cos α = b is

(A) a ellipse

(B) a circle

(C) a straight line

(D) none of these

Q11. A and B are points in the plane such that PA/PB = K (constant) for all points P on a circle. Then the value of K cannot be equal to

(A) –1

(B) 1

(C) 1/2

(D) –1/2

Q12. Equation of chord of a circle x² + y² = 1 whose mid point is (1/2, 1/2) is

(A) x + y = 2

(B) x + y = 1

(C) x – y = 1

(D) none of these

Q13. The range of values of λ for which the circles x² + y² = 4 and x² + y² – 4λx + 9 = 0 have two common tangents, is

(A) λ ∈ [-13/8, 13/8]

(B) λ > 13/8 or λ < –13/8

(C) 1 < λ < 13/8

(D) none of these

Q14. A variable circle passes through the point A (a, b) and touches the x – axis. The locus of the other end of the diameter through A is

(A) (x – a)² = 4by

(B) (y – a)² = 4ax

(C) (x – a)² = 4by

(D) (x + a)² = 4by

Q15. If (mi, 1/mi), mi > 0, i = 1, 2, 3, 4 are four distinct points on a circle, then m₁m₂m₃m₄ is equal to

(A) 1

(B) –1

(C) 2

(D) 0

Answers to Assignment

Question	Answer	Question	Answer	Question	Answer
1.	B	2.	C	3.	A
4.	B	5.	A	6.	A
7.	C	8.	A	9.	A
10.	A	11.	B	12.	B
13.	B	14.	A	15.	B