Quadratic equations

An equation of the form ax² + bx + c = 0, where a ≠ 0 and a, b, c are real numbers, is called a quadratic equation. x = (-b ± √(b² - 4ac)) / 2a are called roots of the quadratic equation ax² + bx + c = 0, a ≠ 0. D = b² - 4ac is called discriminant of the quadratic equation.

Basic Results

• The quadratic equation has real and equal roots if and only if D = 0 i.e. b² - 4ac = 0.
• The quadratic equation has real and distinct roots if and only if D > 0 i.e. b² - 4ac > 0
• The quadratic equation has complex roots with non-zero imaginary parts if and only if D < 0 i.e. b² - 4ac < 0.
• If p + iq (p and q being real) is a root of the quadratic equation where i = √(-1), then p - iq is also a root of the quadratic equation.
• If p + √q is an irrational root of the quadratic equation, then p - √q is also a root of the quadratic equation provided that all the coefficients are rational.
• The quadratic equation has rational roots if D is a perfect square of rational number and a, b, c are rational.
• Let α and β be two roots of the given quadratic equation. Then α + β = -b/a and αβ = c/a.
• A quadratic equation, whose roots are α and β can be written as (x - α)(x - β) = 0. i.e., ax² + bx + c ≡ a(x - α)(x - β).

Illustration 1: If a, b, c are rational then the roots of equation (a + 2b - 3c)x² + (b + 2c - 3a)x + c + 2a - 3b = 0 are

(A) imaginary

(B) rational

(C) irrational

(D) none of these

Solution: (B) Here sum of the coefficients of the given quadratic equation

= (a + 2b - 3c) + (b + 2c - 3a) + (c + 2a - 3b) = 0 ∴ 1 is a root of the given equation.

Since 1 is a rational number, therefore, other root is also rational.

Hence both roots of the given equation are rational.

Quadratic Expression

The expression ax² + bx + c is said to be a real quadratic expression in x where a, b, c are real and a ≠ 0.

Cases for Quadratic Expression f(x) = ax² + bx + c:

(i) a > 0 and b² - 4ac < 0

⇒ f(x) > 0 ∀ x ∈ R.

(ii) a > 0 and b² - 4ac = 0

⇒ f(x) ≥ 0 ∀ x ∈ R.

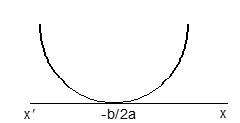
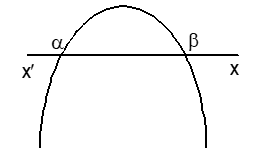
(iii) a > 0 and b² - 4ac > 0

Let f(x) = 0 has two real roots α and β (α < β). Then f(x) > 0 ⇔ x ∈ (-∞, α) ∪ (β, ∞) and f(x) < 0 ⇔ x ∈ (α, β)

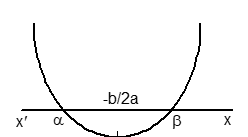
(iv) a < 0 and b² - 4ac < 0

⇒ f(x) < 0 ∀ x ∈ R.

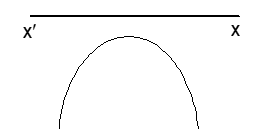
(v) a < 0 and b² - 4ac = 0

⇒ f(x) ≤ 0 ∀ x ∈ R.

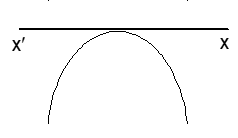
(vi) a < 0 and b² - 4ac > 0

Let f(x) = 0 have two real roots α and β (α < β). Then f(x) < 0 ⇔ x ∈ (-∞, α) ∪ (β, ∞) And f(x) > 0 ⇔ x ∈ (α, β)

Notes

• If a > 0, then minima of f(x) occurs at x = -b/2a and if a < 0, then maxima of f(x) occurs at x = -b/2a
• If f(x) = 0 has two distinct real roots, then a.f(d) < 0 if and only if d lies between the roots and a.f(d) > 0 if and only if d lies outside the roots.

Working Rule to find the range of a Rational Expression in X, where X is real

1. Put the given rational expression equal to y and form the quadratic equation in x.
2. Find the discriminant D of the quadratic equation obtained in step 1.
3. Since x is real, therefore, put D ≥ 0. We get an inequation in y.
4. Solve the above inequation for y. The range of y so obtained determines the range attained by the given rational expression.

Illustration 2: If x is real, then the maximum value of 5 + 4x - x² is

(A) 5

(B) 6

(C) 9

(D) 1

Solution: (C).

Let y = 5 + 4x - x², then x² - 4x + y - 5 = 0 x is real ⇒ 16 - 4(y - 5) ≥ 0 ; ⇒ 4y ≤ 36 ⇒ y ≤ 9 ⇒ maximum value of y = 9.

Condition for Common Roots

Let ax² + bx + c = 0 and dx² + ex + f = 0 have a common root (say α). Then aα² + bα + c = 0 and dα² + eα + f = 0

Solving for α² and α, we get α² = (bf - ce)/(ae - bd) and α = (dc - af)/(ae - bd) ⇒ (dc - af)² = (bf - ce)(ae - bd), which is the required condition for the two equations to have a common root.

• Condition for both the roots to be common is a/d = b/e = c/f.
• If α is a repeated root of the quadratic equation f(x) = ax² + bx + c = 0, then α is also a root of equation f'(x) = 0.

Illustration 3: If a, b, c are in G.P., then the equations ax² + 2bx + c = 0 and dx² + 2ex + f = 0 have a common root if d/a, e/b, f/c are in

(A) A.P.

(B) G.P.

(C) H.P.

(D) none of these

Solution: (A)

a, b, c are in G.P. ⇒ b² - ac = 0 ; Δ₁ = 4b² - 4ac = 0

∴ it has equal roots α = -2b/a or α = -b/a. Since the two equations have common roots therefore α = -b/a must also be a root of 2nd equation.

d(-b/a)² + 2e(-b/a) + f = 0 or

db²/a² - 2eb/a + f = 0 or

db²/a² - 2eb²/ab + fb²/b² = 0 or b² = ac ; or

d/a - 2e/b + f/c = 0 ∴ d/a, e/b, f/c are in A.P.

Illustration 4: If x ∈ R, then (x² + 2x + a)/(x² + 4x + 3a) can take all real values if

(A) a ∈ (0, 2)

(B) a ∈ [0, 1]

(C) a ∈ [-1, 1]

(D) none of these

Solution: (B).

Let y = (x² + 2x + a)/(x² + 4x + 3a), then x²(y - 1) + 2(2y - 1)x + a(3y - 1) = 0.

Since x ∈ R, the discriminant of the above quadratic must be non-negative, so, 4(2y - 1)² - 4(y - 1)a(3y - 1) ≥ 0 for all y ∈ R

⇒ (4 - 3a)y² - 4(1 - a)y + 1 - a ≥ 0 for all y ∈ R ⇒ 4 - 3a > 0 and disc. ≤ 0

⇒ a < 4/3 and 16(1 - a)² - 4(1 - a)(4 - 3a) ≤ 0 ⇒ a < 4/3 and a(a - 1) ≤ 0 ⇒ a < 4/3 and 0 ≤ a ≤ 1 ⇒ 0 ≤ a ≤ 1.

Exercise 1

(i) The value of m for which the equation x² - 2x(1 + 3m) + 7(3 + 2m) = 0 has equal roots

(A) -10/9, 2

(B) -10/9, -2

(C) -10/2, 2

(D) -10/9, -2

(ii) The least value of 40 - 12x + x² when x is real is

(A) 28

(B) 4

(C) -4

(D) 0

(iii) The values of 'a' for which the equation 2x² - 2(2a+1)x + a(a-1) = 0 has roots α and β where α < a < β are such that

(A) a > -3

(B) a < 0

(C) a > 0 or a < (-3 + √7)/2

(D) none of these

Illustration 5: If α, β are the roots of the equation 2x² + 6x + a = 0, a < 0, then α/β + β/α is less than

(A) -2

(B) -4

(C) -8

(D) none of these 

Solution: (A). Here α + β = -3 and αβ = a/2

α/β + β/α = (α² + β²)/(αβ) = ((α + β)² - 2αβ)/(αβ) = ((-3)² - 2(a/2))/(a/2)

= (9 - a)/(a/2) = (18 - 2a)/a (∵ a < 0) ∴ α/β + β/α < -2.

Illustration 6

If α and β are the roots of the equation, 2x² - 3x - 6 = 0, then equation whose roots are α² + 2, β² + 2 is

(A) 4x² + 49x + 118 = 0

(B) 4x² - 49x + 118 = 0

(C) 4x² - 49x - 118 = 0

(D) x² - 49x + 118 = 0

Solution: (B).

α + β = 3/2, αβ = -6/2 = -3 S = α² + 2 + β² + 2 + 4 = (α+β)² - 2αβ + 4 = 49/4

P = α²β² + 2(α² + β²) + 4 = α²β² + 4 + 2[(α+β)² - 2αβ] = 118/4.

Therefore, the equation is x² - (49/4)x + (118/4) = 0 ⇒ 4x² - 49x + 118 = 0.

Exercise 2

(i) If (x² + 2x + 7)/(2x + 3) < 6, x ∈ R, then

(A) x > 11 or x < -3/2

(B) x > 11 or x < 1

(C) -3/2 < x < 1

(D) 1 < x < 11 or x < -3/2

(ii) If α, β are roots of the quadratic equation x² + bx - c = 0, then the equation whose roots are b and c is

(A) x² + ((αβ) + (α + β))x + (αβ)(α + β) = 0

(B) x² - ((αβ) + (α + β))x + (αβ)(α + β) = 0

(C) x² + ((αβ)+(α + β))x +(αβ)+(α + β) = 0

(D) none of these

(iii) If α, β be the roots of 4x² - 16x + λ = 0, λ ∈ R, such that 1 < α < 2 and 2 < β < 3 then the number of integral solutions of λ is

(A) 5

(B) 6

(C) 2

(D) 3

Exercise 3

(i) For all x ∈ R, if mx² - 9mx + 5m + 1 > 0, then m lies in the interval

(A) (-4/61, 0)

(B) (0, 4/61)

(C) [0, 4/61]

(D) none of these

(ii) The harmonic mean of the roots of the equation (5 + √2)x² - (4 + √5)x + (8 + 2√5) = 0 is

(A) 2

(B) 4

(C) 7

(D) 8

(iii) If one root of the equation ax² + bx + c = 0 is nth power of the other, then (aⁿc)^(1/(n+1)) + (acⁿ)^(1/(n+1)) is equal to

(A) -b

(B) b

(C) a

(D) none of these

Inequations

Quadratic Inequations

Let f(x) = ax² + bx + c be a quadratic expression. Then inequations of the type f(x) ≤ 0 or f(x) ≥ 0 are known as quadratic inequations. The study of these can be easily done by taking the corresponding quadratic expression and by applying the basic results of quadratic expression.

Illustration 9:

The value of x in the inequation √(x + 14) < (x + 2)

(A) x ∈ (2, ∞)

(B) x ∈ (1, 2)

(C) x ∈ (1, ∞)

(D) none of these

Solution: (A). We have √(x + 14) < (x + 2). This inequation is equivalent to the system

x + 14 ≥ 0 x + 2 > 0 x + 14 < (x + 2)² ⇒ x ≥ -14 x > -2 x² + 3x - 10 > 0 ⇒ x ≥ -14 x > -2 (x - 5)(x + 2) > 0 ⇒ x ≥ -14 x > -2 x > 5 or x < -2

Combining all three inequation of system, we get x > 2 i.e. x ∈ (2, ∞).

Answer to Exercises

Exercise 1

 (i) C

(ii) B

(iii) C

Exercise 2

(i) D

(ii) A

(iii) D

Exercise 3

(i) C

(ii) B

(iii) A

Formulae and Concepts at a Glance

• An equation of the form ax² + bx + c = 0, where a ≠ 0 and a, b, c are real numbers, is called a quadratic equation.
• The roots of the quadratic equation are given by x = (-b ± √(b² - 4ac))/2a.
• The quantity D (D = b² - 4ac) is known as the discriminant of the equation.
• Let α and β be two roots of the given quadratic equation. Then α + β = -b/a and αβ = c/a.
• A quadratic equation, whose roots are α and β can be written as (x - α)(x - β) = 0 i.e., ax² + bx + c ≡ a(x - α)(x - β).
• If the quadratic equation is satisfied by more than two distinct numbers (real or complex), then it becomes an identity, i.e. a = b = c = 0.
• The quadratic equation has real and equal roots if and only if D = 0 i.e. b² - 4ac = 0.
• The quadratic equation has real and distinct roots if and only if D > 0 i.e. b² - 4ac > 0
• The quadratic equation has complex roots with non-zero imaginary parts if and only if D < 0 i.e. b² - 4ac < 0.
• If p + iq (p and q being real) is a root of the quadratic equation where i = √(-1), then p - iq is also a root of the quadratic equation.
• If p + √q is an irrational root of the quadratic equation, then p - √q is also a root of the quadratic equation provided that all the coefficients are rational.
• The quadratic equation has rational roots if D is a perfect square and a, b, c are rational.
• Condition for both the roots to be common is a/d = b/e = c/f.

The expression ax² + bx + c is said to be a real quadratic expression in x where a, b, c are real and a ≠ 0. Let f(x) = ax² + bx + c where a, b, c ∈ R (a ≠ 0).

f(x) can be rewritten as f(x) = a[(x + b/2a)² + (4ac - b²)/4a²] = a[(x + b/2a)² - D/4a²], where D = b² - 4ac is the discriminant of the quadratic expression.

Solved Examples

Ques 1. The equation (cos p - 1)x² + (cos p)x + sin p = 0, in the variable x, has real roots. Then p can take any value in the interval

(A) (0, 2π)

(B) (-π, 0)

(C) (-π/2, π/2)

(D) (0, π)

Sol. (D). Since the quadratic in x has real roots cos²p - 4(cos p - 1) sin p ≥ 0 ; or cos²p - 4sin p cos p + 4sin p ≥ 0

or (cos p - 2sin p)² + 4sin p - 4sin²p ≥ 0 ; or (cos p - 2sin p)² + 4sin p(1 - sin p) ≥ 0

Hence p can take any value in (0, π).

Ques 2. The equation: (3 log₂ x + 5)/(4) + log₂ x/(4) = √2 has

(A) at least one real solution

(B) exactly one real solutions

(C) exactly one irrational solution

(D) complex roots

Sol. (C). Let log₂x = a, then x = 2ᵃ

Hence, (3a + 5)/4 + a/4 = 2^(a-1/2) ⇒ (4a + 5)/4 = 2^(a-1/2) ⇒ 3a + 4a² - 5a - 2 = 0 ⇒ 3a³ + 4a² - 5a - 2 = 0

⇒ a = 1, a = -2, a = -1/3 ⇒ x = 2, x = 1/4, x = 1/∛2.

All the three roots are real and one of them is irrational.

Ques 3. If b > a, then the equation (x - a)(x - b) + 1 = 0, has

(A) both roots in (-∞, a)

(B) both roots in (b, ∞)

(C) both roots in (a, b)

(D) one root in (-∞, a) and other in (b, ∞)

Sol. (C). (x - a)(x - b) + 1 = 0 ; ⇒ (x - a)(x - b) = -1 < 0 ⇒ a < x < b.

Ques 4. If the equation 3x² + 2(b² + 1)x + (b² - 3b + 2) = 0 possess roots of opposite sign, then b lies in

(A) (-∞, 1)

(B) (-∞, 0)

(C) (1, 2)

(D) (3/2, 2)

Sol. (C). 3x² + 2(b² + 1)x + (b² - 3b + 2) = 0 will have two roots of opposite sign if it has real roots and the product of the roots is negative.

i.e., 4(b² + 1)² - 12(b² - 3b + 2) ≥ 0 and (b² - 3b + 2)/3 < 0.

Both these conditions are fulfilled if b² - 3b + 2 < 0 i.e., if (b - 1)(b - 2) < 0 ⇒ 1 < b < 2.

Alternative: Here a > 0, equation possess roots of opposite sign if f(0) < 0 ⇒ b² - 3b + 2 < 0

⇒ (b - 1)(b - 2) < 0 ; ⇒ b ∈ (1, 2).

Ques 5. If α, β are the roots of the equation a(x² - 1) + 2bx = 0, then the equation whose roots are 2α + 1/β, 2β + 1/α is

(A) bx² + 2ax - b = 0

(B) ax² + 2bx - a = 0

(C) ax² + 2bx + a = 0

(D) x² + 2(a + b)x - ab = 0

Sol. (C). α + β = -2b/a, αβ = -1 Now, required equation having roots 2α + 1/β, 2β + 1/α

Sum = 2α + 1/β + 2β + 1/α = 2(α + β) + (α + β)/(αβ) = 2(-2b/a) + (-2b/a)/(-1) = -4b/a + 2b/a = -2b/a

Product = (2α + 1/β)(2β + 1/α) = 4αβ + 2 + 2 + 1/(αβ) = 4(-1) + 4 + 1/(-1) = -4 + 4 - 1 = -1

Required equation is x² - (-2b/a)x + (-1) = 0 ⇒ ax² + 2bx - a = 0.

Ques 6. Solution set of x^(2log x) = 10x² is

(A) {1 + √3, 1 - √3}

(B) {1, -1}

(C) {10^((1-√3)/2), 10^((1+√3)/2)}

(D) {10^(1-√3), 10^(1+√3)}

Sol. (D). The given equation exist for x > 0

Now, x^(2log x) = 10x² ⇒ log(x^(2log x)) = log 10x² ⇒ 2(log x)² = 1 + 2log x . Let log x = y

⇒ 2y² - 2y - 1 = 0 ⇒ y = (2 ± √(4 + 8))/2 ⇒ y = 1 ± √3 log₁₀x = 1 ± √3 ⇒ x = 10^(1±√3).

Ques 7. If x is real, then (x² + 34x - 71)/(x² + 2x - 7) cannot have values between

(A) 1 and 3

(B) 5 and 9

(C) 11 and 14

(D) -2 and 0

Sol. (B). Let y = (x² + 34x - 71)/(x² + 2x - 7) ⇒ x²(y - 1) + 2(y - 17)x - (7y - 71) = 0

Since x is real, therefore above equation has real roots. ∴ D ≥ 0

⇒ 4(y - 17)² + 4(y - 1)(7y - 71) ≥ 0 ; ⇒ y² - 14y + 45 ≥ 0 ; y ≤ 5 or y ≥ 9.

Ques 8. If x is real, then the value of k for which |x² + kx + 1|/(x² + x + 1) < 2 is valid is/are

(A) k = 4

(B) k = 0

(C) 0 < k < 4

(D) 0 ≤ k ≤ 4

Sol. (C). |x² + kx + 1|/(x² + x + 1) < 2 ∀ x ∈ R ⇒ -2 < (x² + kx + 1)/(x² + x + 1) < 2 ⇒ 2(x² + x + 1) < x² + kx + 1 < 2(x² + x + 1)

⇒ 3x² + (k + 2)x + 3 > 0 and x² + (2 - k)x + 1 > 0

⇒ (k + 2)² - 36 < 0 and (2 - k)² - 4 < 0 ⇒ (k - 4)(k + 8) < 0 and k(k - 4) < 0

⇒ -8 < k < 4 and 0 < k < 4. Therefore 0 < k < 4.

Ques 9. a, b, c are positive real numbers forming an A.P. If ax² + bx + c = 0 has real roots then

(A) (a/c) + (c/a) ≥ 2√3

(B) (a/c) - (c/a) ≤ 2√3

(C) (a/c) + (c/a) ≥ 2√3

(D) none of these

Sol. (A). Since a, b, c are in A.P. therefore b = (a + c)/2, since roots of the equation ax² + bx + c = 0 are real ⇒ D ≥ 0 ⇒ b² - 4ac ≥ 0

((a + c)/2)² - 4ac ≥ 0 a² + c² - 14ac ≥ 0

dividing by c² we get, (a²/c²) - 14(a/c) + 1 ≥ 0

((a/c) - (a/c) - 14) ≥ 0

⇒ ((a/c) - (c/a))² ≥ 12 (since a,c > 0 given)

⇒ (a/c) - (c/a) ≥ 2√3 or (a/c) - (c/a) ≤ -2√3

But (a/c) - (c/a) ≤ -2√3 is not possible  ∴ (a/c) + (c/a) ≥ 2√3

Ques 10. If x² + y² + z² = 1, then the value of xy + yz + zx lies in the interval

(A) [-1/2, 2]

(B) [-1, 2]

(C) [-1/2, 1]

(D) [-1, 1/2]

Sol. (C). Let xy + yz + zx = λ,

then x² + y² + z² - λ = 1 - λ = (1/2)[2(x - y)² + 2(y - z)² + 2(z - x)²] ≥ 0

⇒ 1 - λ ≥ 0 ⇒ λ ≤ 1

Again (x + y + z)² = x² + y² + z² + 2λ

= 1 + 2λ ≥ 0 ⇒ λ ≥ -1/2

Assignment Problems

Q1. The number of real solutions of the equation |x|² - 4|x| + 3 = 0 is

(A) 4

(B) 2

(C) 1

(D) 3

Q2. Let α, β be the roots of the equation (x - a)(x - b) = c, c ≠ 0. Then the roots of the equation (x - α)(x - β) + c = 0 are

(A) a, c

(B) b, c

(C) a, b

(D) a + c, b + c

Q3. The number of real solutions of x - 1/(x² - 4) = 2 - 1/(x² - 4) is

(A) 0

(B) 1

(C) 2

(D) infinite

Q4. If x = √(6 + √(6 + √(6 + ......))), then

(A) x is an irrational number

(B) 2 < x < 3

(C) x = 3

(D) none of these

Q5. If x^(2/3) - 7x^(1/3) + 10 = 0, then x =

(A) {125}

(B) {8}

(C) φ

(D) {125, 8}

Q6. The quadratic equation whose one roots is 1/(2 + √5) will be

(A) x² + 4x - 1 = 0

(B) x² + 4x + 1 = 0

(C) x² - 4x - 1 = 0

(D) 2x² - 4x + 1 = 0

Q7. The value of p for which (x - 1) is a factor of x³ + (p + 1)²x² - 10 is given by

(A) 4, 2

(B) 2, -4

(C) -2, 4

(D) none of these

Q8. The greatest negative integer satisfying x² - 4x - 77 < 0 and x² > 4 is

(A) -5

(B) -6

(C) -3

(D) none of these.

Q9. If the roots of the equation x² - 2ax + a² + a - 3 = 0 are less than 3, then

(A) a < 2

(B) 2 ≤ a ≤ 3

(C) 3 < a ≤ 4

(D) a > 4

Q10. If one root of the equation (k² + 1)x² + 13x + 4k = 0 is reciprocal of the other, then k has the value

(A) ±2√3

(B) ±2√3

(C) ±1

(D) none of these

Q11. If 1/(4 - 3i) is a root of ax² + bx + 1 = 0, where a, b are real, then

(A) a = 25, b = -8

(B) a = 25, b = 8

(C) a = 5, b = 4

(D) none of these

Q12. If sin θ and cos θ are the roots of the equation ax² + bx + c = 0 then

(A) (a + c)² = b² + c²

(B) (a + c)² = b² - c²

(C) (a - c)² = b² + c²

(D) (a - c)² = b² - c²

Q13. If 4ac > b² and 9a + c > 3b for the quadratic expression ax² + bx + c = 0, then

(A) a < 0

(B) a + b + c < 0

(C) c < 0

(D) 4a + 2b + c > 0

Q14. If a < b < c < d, then roots of the equation (x - a)(x - c) + λ(x - b)(x - d) = 0 (λ ∈ R and λ ≠ -1) are

(A) always real

(B) always rational

(C) lie between b and d

(D) lie between a and c

Q15. If roots of the equation x² + bx + c = 0 are opposite in sign, then

(A) c > 0

(B) c < 0

(C) b² = 4c

(D) c > b²/4

Answers to Assignment

1. A

2. C

3. A

4. C

5. D

6. A

7. B

8. B

9. A

10. B 

11. A

12. A

13. D

14. A

15. B