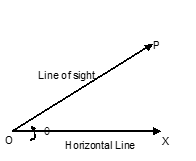
Angle of Elevation
If 'O' be the observer's eye and OX be the horizontal line through O. If the object P is at a higher level than eye, then angle POX = θ is called the angle of elevation.
Angle of Depression
If the object P is at a lower level than O, then angle POX is called the angle of depression.
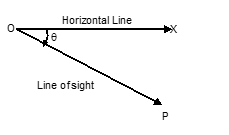
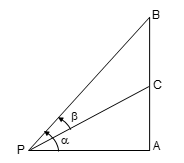
Illustration 1: A ladder leaning against a vertical wall is inclined at an angle α to the horizontal. On moving its foot 2 m away from the wall, the ladder is now inclined at angle β. Then the vertical distance moved by the ladder is
(A) 2 sin β/(sin β – sin α)
(B) 2 cos β/(sin β – sin α)
(C) sin β cos β/(sin β – sin α)
(D) 2 cos β/(sin β + sin α)
Solution: (B)
From triangle ABC:
l = 2 sec α ...(1)
x + d = 2 tan α ...(2)
From triangle CDE:
x = l sin β ...(3)
From (1) and (3): x = 2 sec α sin β
Putting in (2): 2 sec α sin β + d = 2 tan α
d = 2 tan α – 2 sec α sin β
d = (2 sin α/cos α) – (2 sin β/cos α)
d = (2/cos α)(sin α – sin β)
Therefore: d = (2/cos β)(sin β – sin α)
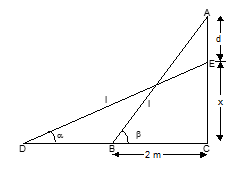
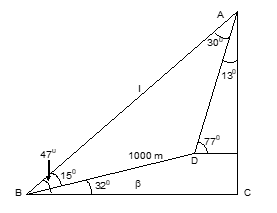
Illustration 2: The altitude of a rock is observed to be 47°. After walking 1000 m towards it, up a slope inclined at 32° to the horizon, the altitude is 77°. Then the vertical height of the rock above the first point of observation is (given that sin 47° = 0.73)
(A) 730√2 m (B) 730 m (C) 730/√2 m (D) none of these
Solution: (A)
In triangle ABD:
l/1000 = sin 30°/sin 45°
l = 2000 × (1/2) = 1000√2
AC = l sin 47°
AC = 1000√2 × 0.73 = 730√2 m
Exercise Problems:
(i) A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 40 feet from the bank, he finds the angle to be 30°. Then the height of the tree is
(A) 20 ft
(B) 20√3 ft
(C) 30√3 ft
(D) 20√2 ft
(ii) The angular depressions of the top and the foot of a chimney as seen from the top of a second chimney which is 150 meters high and standing on the same level as the first are α and β respectively. Then the distance between their tops, when tan α = 4/3, tan β = 5/2 is
(A) 100 m (B) 120 m (C) 110 m (D) none of these
Exercise 1 Answers:
(i) B
(ii) A
Formulas and Concepts at a Glance
Key Concepts:
-
If 'O' be the observer's eye and OX be the horizontal line through O. If the object P is at a higher level than eye, then angle POX = θ is called the angle of elevation
-
If the object P is at a lower level than O, then angle POX is called the angle of depression.
Solved Examples
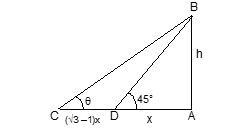
1. Length of the shadow of a person is x when the angle of elevation of the sun is 45°. If the length of the shadow increases by (√3 – 1)x, then the angle of elevation of sun should become
(A) 15° (B) 18° (C) 25° (D) 30°
Solution: (D) Let h be the height of the person
h/x = tan 45° = 1 ⟹ h = x
Now, tan θ = h/[x + (√3 – 1)x] = x/(√3x) = 1/√3
Therefore θ = 30°
2. At a certain point the angle of elevation of a tower is found to be such that its cotangent is 3/5; on walking 32 m directly towards the tower its angle of elevation is an angle whose cotangent is 2/3. Then the height of tower is
(A) 120 m (B) 80 m (C) 160 m (D) 210 m
Solution: (C)
AB = tower
cot ∠ADB = 3/5 ⟹ BD/AB = 3/5 ⟹ (32 + BC)/AB = 3/5
AB = (5/3)(32 + BC) ...(1)
cot ∠ACB = 2/3 ⟹ BC/AB = 2/3 ⟹ (2/3)BC = AB ...(2)
From (1) and (2): (2/3)BC = (5/3)(32 + BC) ⟹ BC = 64 m
AB = (5/2) × 64 = 160 m
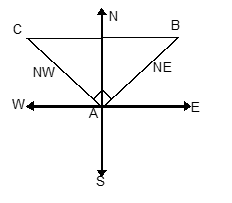
3. A light house, facing north, sends out a fan shaped beam of light extending from NE (north east) to NW (north west). An observer on a steamer, sailing due west, first sees the light when he is 5 km away from the light house and continues to see it for 30√2 minutes. Then speed of the steamer is
(A) 5 km/h
(B) 15 km/h
(C) 20 km/h
(D) 10 km/h
Solution: (D)
Light house is at A and it throws the light from direction AB to AC.
AB = AC = 5 km, ∠BAC = 90°
BC = 5√2 km
Speed of streamer = (5√2)/(30√2/60) = 10 km/h
4. The angle of elevation of the top of a T.V. tower from three points A, B, C in a straight line in the horizontal plane through the foot of the tower are α, 2α, 3α respectively. If AB = a, the height of the tower is
(A) a tan α (B) a sin α (C) a sin 2α (D) a sin 3α
Solution: (C)
AB = a, BP = a from isosceles triangle ABP
h = BP sin 2α = a sin 2α
5. A man on the top of a cliff 100 meter high, observes the angles of depression of two points on the opposite sides of the cliff as 30° and 60° respectively. Find the distance between the two points.
(A) 400/√3 meters (B) 100√3 meter (C) 400 meter (D) none of these
Solution: (A)
Let PQ be the cliff and A and B be the points under observation.
PQ = 100 meters
AP = 100 cot 30° = 100√3
BP = 100 cot 60° = 100/√3
Hence AB = AP + BP = 100√3 + 100/√3 = 400/√3 m
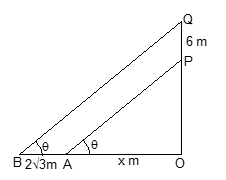
6. A flag–staff of 6 m high placed on the top of a tower throws a shadow of 2√3 m along the ground. Then the angle that the sun makes with the ground is:
- 60°
- 30°
- 45°
- none of these
Solution (Answer: A)
Let the tower’s height be h. Let the tower’s shadow be x. The sun makes an angle θ with the ground.
tan θ = h / x and tan θ = (h + 6) / (x + 2√3)
⇒ h(x + 2√3) = x(h + 6) ⇒ 2√3 h = 6x ⇒ x = h / √3
tan θ = h / x = √3 ⇒ θ = 60°.
Angle with the ground = 60°
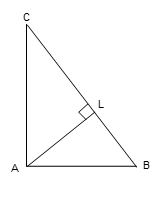
7. ABC (right-angled at A), the hypotenuse is 2√2 times the length of the perpendicular from A to the hypotenuse. Then the angles B and C are:
- 67.5° and 22.5°
- 68.5° and 21.5°
- 70° and 20°
- none of these
Answer: A
Let L be the foot of the perpendicular from A to the hypotenuse BC. Then BC = 2√2 · AL, and
BL/AL + LC/AL = BC/AL ⇒ cot B + cot C = 2√2.
Since B + C = 90°, we have cot C = tan B. Hence,
cot B + tan B = 2√2 ⇒ 2 csc(2B) = 2√2 ⇒ csc(2B) = √2.
2B = 45° or 135° ⇒ B = 22.5° or 67.5°; then C = 67.5° or 22.5°.
Angles: B = 67.5°, C = 22.5° (or vice-versa)
8. A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he returns 100 m from the bank, he finds the angle to be 30°. Then the height of the tree is:
- 80√3 m
- 60√3 m
- 80 m
- 50√3 m
Solution (Answer: D)
Let AB = h (height of tree), CB = x (breadth of river). ∠BCA = 60°. Let D be second position of man so that ∠BDA = 30°.
tan 60° = h/x ⇒ h = √3x ...(1)
tan 30° = h / (100 + x) = 1/√3 ⇒ h = (100 + x)/√3 ...(2)
From (1) and (2): √3(√3x) = 100 + x ⇒ 3x − x = 100 ⇒ x = 50. So, h = 50√3.
Height of the tree = 50√3 m
9. AB is a vertical pole. A is on the ground. C is the midpoint of AB. P is a point on the ground. The portion CB subtends angle β at P. If AP = n·AB, then tan β is:
- n / (2n² + 1)
- n / (2n² − 1)
- n / (n² + 1)
- none of these
Solution (Answer: A)
Given AP = n·AB.
∠APB = α, ∠APC = α − β
From △APB: tan α = AB / AP = 1/n
From △APC: tan(α − β) = AC / AP = (1/2·AB) / (n·AB) = 1/(2n)
So tan β = tan α − tan(α − β) / (1 + tan α·tan(α − β))
= (1/n − 1/(2n)) / (1 + (1/n)(1/(2n)))
= (1/(2n)) / ((2n² + 1)/(2n²))
= n / (2n² + 1)
tan β = n / (2n² + 1)
Assignment Problems
1. The angle of elevation of the top of a hill from each of the vertices A, B and C of a horizontal triangle is α. The height of the hill is
(A) b tan α cosec B (B) (1/2)a tan α cosec A (C) (1/2)c tan α cosec C (D) none of these
2. The upper (3/4)th portion of a vertical pole subtends an angle θ = tan⁻¹(3/5) at a point in horizontal plane through its foot and at a distance 40 m from it. The height of the pole is
(A) 140 m (B) 100 m (C) 40 m (D) 200 m
3. A person stands at a point A due south of a tower and observes that its elevation is 60°. He then walks westward towards B, where elevation is 45°. At a point C on AB produced, he finds to be 30°, then AB:BC is
(A) 50/√3 m (B) 75/√3 m (C) 50 m (D) 75 m
4. A person walking along a straight road observes that at two points 1 km apart, the angle of elevation of pole in front of him are 30° and 75°. The height of the pole is
(A) 250/(√3 + 1) m (B) 150/(√3 + 1) m (C) 225/(√2 + 1) m (D) 225/(√2 - 1) m
5. A pole of 50 meter high stands on a building 250 m high. To an observer at a height of 300 m, the building and the pole subtend equal angles. The distance of the observer from the top of the pole is
(A) 25√6 m (B) 50 m (C) 25√3 m (D) 25 m
6. At a point on a level plane a tower subtends an angle α and a flag staff a ft. in length at the top of the tower subtends an angle β. The height of the tower is
(A) a sin α cos β/(cos α - cos β) (B) a sin α cos β/(sin α - sin β) (C) a cos α/(sin α sin β) (D) none of these
7. A tower AB leans towards west making an angle θ with the vertical. The angular elevation of B the top most point of the tower is α as observed from a point C due east of A at a distance d from A. If the angular elevation of B from a point due east of C at a distance 2d from C is β, then
(A) 2 tan β = 2 cot α - cot θ (B) 2 tan β = 3 cot α - cot θ (C) tan β = cot α - cot θ (D) none of these
8. An observer standing on a 300 m high tower observes two boats in the same direction, their angle of depression are 60° and 30° respectively. The distance between the boats is
(A) 173.2 m (B) 346.4 m (C) 25 m (D) 72 m
9. A harbour lies in a direction 60° south of west from a fort, and at a distance 30 km from it, a ship sets out from the harbour at noon and sails due east at 10 km an hour. The ship will be 70 km from the fort at
(A) 7 P.M. (B) 8 P.M. (C) 5 P.M. (D) 10 P.M.
10. A man on a cliff observes a boat sailing towards the shore at a uniform speed to the point immediately beneath him, the angle of depression of the boat is 30°. 3 minutes later the depression is found to be 60°. The time taken by the boat to reach the shore is
(A) 2 minutes (B) 1.5 minutes (C) 3 minutes (D) 4 minutes
11. If the angle of elevation of a cloud from a point h meters above a lake be α and the angle of depression of its reflection in the lake be β, then the distance of the cloud from the point of observation is
(A) 2h sin α/sin(β - α) (B) h cos α/sin(β - α) (C) 2h cos α/sin(β - α) (D) none of these
12. A tower subtends angle α, 2α, 3α at three points A, B and C respectively lying on a horizontal line through the foot of the tower. Then AB/BC is equal to
(A) 3 - 4sin²α (B) sin 3α/sin 2α (C) sin 2α/sin α (D) sin 3α/cos α
13. A tower subtends an angle α at a point A in the plane of its base and the angle of depression of the foot of the tower at a point b ft just above A is β. Then the height of the tower is
(A) b tan α tan β (B) b cot β/(cot α - cot β) (C) b tan β/(sin α tan β) (D) b cot α cot β
14. The height of a house subtends a right angle at the opposite window. The angle of elevation of window from the base of the house is 60°. If the width of the road be 6 meters, then the height of the house is
(A) 8√3 m (B) 8 m (C) 6 m (D) 6√3 m
15. From the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of a tower. The height of the tower is
(A) h sin α cos(α - β)/cos β (B) h sin α cos(α - β)/sin β (C) h sin α/sin(α - β) cos β (D) h sin α/sin(α - β) sin β
Answers to Assignment Problems
| Problem | Answer | Problem | Answer | Problem | Answer |
|---|---|---|---|---|---|
| 1 | B | 6 | C | 11 | C |
| 2 | C | 7 | B | 12 | A |
| 3 | B | 8 | B | 13 | B |
| 4 | A | 9 | B | 14 | A |
| 5 | A | 10 | B | 15 | B |