Understanding Trigonometric Equations and Their General Solutions
Trigonometric equations form a fundamental component of advanced mathematics, appearing frequently in competitive examinations like JEE, NEET, and other engineering entrance tests. These equations involve trigonometric functions and require systematic approaches to find all possible solutions within specified intervals or general solution sets.
The complexity of trigonometric equations stems from the periodic nature of trigonometric functions. Unlike algebraic equations that typically have finite solutions, trigonometric equations often yield infinite solution sets due to the cyclical behavior of sine, cosine, and tangent functions. Understanding the general solution methodology becomes crucial for identifying all possible values that satisfy a given trigonometric equation.
Essential Formulas for Trigonometric Equations
The foundation of solving trigonometric equations lies in mastering the general solution formulas. These formulas leverage the periodic properties of trigonometric functions to express infinite solution sets in compact mathematical notation.
| Equation Type | General Solution | Description |
|---|---|---|
| sin θ = 0 | θ = nπ | Where n is any integer |
| cos θ = 0 | θ = (2n + 1)π/2 | Odd multiples of π/2 |
| tan θ = 0 | θ = nπ | Where n is any integer |
| sin θ = sin α | θ = nπ + (-1)ⁿα | Where α ∈ [-π/2, π/2] |
| cos θ = cos α | θ = 2nπ ± α | Where α ∈ [0, π] |
| tan θ = tan α | θ = nπ + α | Where α ∈ (-π/2, π/2) |
| sin²θ = sin²α | θ = nπ ± α | Solutions for squared functions |
| cos²θ = cos²α | θ = nπ ± α | Solutions for squared functions |
| tan²θ = tan²α | θ = nπ ± α | Solutions for squared functions |
| sin θ = 1 | θ = (4n + 1)π/2 | Maximum value of sine |
| cos θ = 1 | θ = 2nπ | Maximum value of cosine |
| cos θ = -1 | θ = (2n + 1)π | Minimum value of cosine |
Critical Guidelines for Solving Trigonometric Equations
Successfully solving trigonometric equations requires adherence to specific mathematical principles that prevent common errors and ensure complete solution sets. These guidelines represent accumulated expertise from advanced mathematical practice and competitive examination preparation.
Avoiding Mathematical Pitfalls: Never square trigonometric equations unnecessarily, as this process can introduce extraneous roots that don't satisfy the original equation. When squaring becomes unavoidable, always verify solutions by substituting back into the original equation. Similarly, avoid canceling terms containing unknown variables from both sides of an equation when they appear in product form, as this may eliminate valid solutions.
Domain and Range Considerations: Maintain awareness of function domains throughout the solving process. Ensure that denominators never equal zero and that all trigonometric expressions remain within their defined ranges. The solution process should preserve the original equation's domain restrictions.
Solution Set Optimization: Trigonometric equation solutions often contain redundant or overlapping sets. Carefully analyze solution families to eliminate repetitions and present the most concise general solution. When multiple solution sets share common values, consolidate them to avoid duplication in the final answer.
Advanced Solving Techniques and Applications
Complex trigonometric equations frequently require transformation techniques that convert them into more manageable forms. These methods include using trigonometric identities, substitution techniques, and graphical analysis approaches.
Identity-Based Transformations: Leverage fundamental trigonometric identities such as Pythagorean identities, sum-to-product formulas, and double-angle formulas to simplify complex equations. For equations involving multiple trigonometric functions, converting everything to a single function type often reveals clear solution paths.
Substitution Methods: Strategic substitutions can transform complicated trigonometric equations into familiar algebraic forms. For instance, setting u = sin θ or u = cos θ can convert trigonometric equations into quadratic equations in u, which are readily solvable using standard algebraic techniques.
Interval-Specific Solutions: While general solutions provide complete solution sets, many practical problems require solutions within specific intervals. Understanding how to extract particular solutions from general solution formulas becomes essential for examination success and real-world applications.
The systematic approach to trigonometric equations, supported by these comprehensive formulas and guidelines, provides students with robust problem-solving frameworks applicable across various mathematical contexts and competitive examination scenarios.
Since trigonometrical functions are periodic functions, solutions of trigonometric equations can be generalized with the help of the periodicity of the trigonometrical functions. The solution consisting of all possible solutions of a trigonometric equation is called its general solution.
Fundamental Formulas for Solving Trigonometric Equations
sin θ = 0 ⟹ θ = nπ
cos θ = 0 ⟹ θ = (2n + 1)π/2
tan θ = 0 ⟹ θ = nπ
sin θ = sin α ⟹ θ = nπ + (–1)ⁿα, where α ∈ [–π/2, π/2]
cos θ = cos α ⟹ θ = 2nπ ± α, where α ∈ [0, π]
tan θ = tan α ⟹ θ = nπ + α, where α ∈ (–π/2, π/2)
sin²θ = sin²α, cos²θ = cos²α, tan²θ = tan²α ⟹ θ = nπ ± α
sin θ = 1 ⟹ θ = (4n + 1)π/2
cos θ = 1 ⟹ θ = 2nπ
cos θ = –1 ⟹ θ = (2n + 1)π
sin θ = ± sin α and cos θ = ± cos α ⟹ θ = 2nπ + α
Important Points to Remember
- While solving a trigonometric equation, squaring the equation at any step should be avoided as far as possible. If squaring is necessary, check the solution for extraneous roots.
- Never cancel terms containing unknown terms on the two sides, which are in product. It may cause loss of genuine solution.
- The answer should not contain such values of angles which make any of the terms undefined or infinite.
- Domain should not be changed. If it changes, necessary corrections must be made.
- Check that denominator is not zero at any stage while solving equations.
- At times you may find that your answers differ from those in the package in their notations. This may be due to the different methods of solving the same problem. Whenever you come across such situation, you must check their identity.
- While solving trigonometric equations, you may get same set of solutions repeated in your answer. It is necessary for you to exclude those repetitions.
For example, in nπ + π/2, kπ/5 + π/10 (n, k ∈ I), the set nπ + π/2 forms a part of the second set of solutions (you can check by putting k = 5m + 2 (m ∈ I). Hence the correct answer would be kπ/5 + π/10, k ∈ I.
- Sometimes the two solution sets consist partly of common values. In all such cases the common part must be presented only once.
Illustration 1: For the equation sin²θ – cos θ = 1/4, the values of θ in the interval 0 ≤ θ ≤ 2π, are
(A) π/6, 5π/6
(B) 7π/6, 11π/6
(C) π/3, 2π/3
(D) π/3, 5π/3
Solution: (D)
The given equation can be written as 1 – cos²θ – cos θ = 1/4
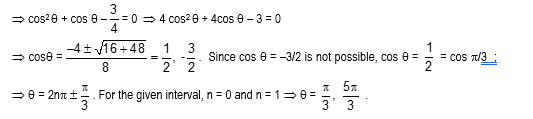
Illustration 2:
The general solutions of the equation sin 6θ = sin 4θ – sin 2θ are given by
(A) 2nπ ± π/6, n ∈ I
(B) 2nπ ± π/4, n ∈ I
(C) nπ ± π/4, m, m, n ∈ I
(D) (2l + 1)π/6, (2m + 1)π/4, nπ, l, m, n ∈ I
Solution: (D)
sin 6θ = sin 4θ – sin 2θ ⟹ 2 sin 3θ cos 3θ = 2 cos 3θ. sin θ
⟹ 2 sin 3θ cos 3θ – 2 cos 3θ. sin θ = 0
⟹ 2 cos 3θ (sin 3θ – sin θ) = 0 ⟹ 4 cos 3θ cos 2θ sin θ = 0
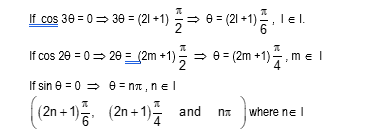
Illustration 3:
The most general solution of the equation cos θ + √3 sin θ = √2 is
(A) nπ + (-1)ⁿπ/4, n ∈ I
(B) nπ + π/4, n ∈ I
(C) nπ + (-1)ⁿπ/6, n ∈ I
(D) none of these
Solution: (D)
Dividing the equation by √(1² + (√3)²) = √4 = 2
.png)
Exercise Problems
Exercise 1:
(i) The general solution of the equation 7cos²θ + 3 sin²θ = 4 is given by
(A) 2nπ ± π/3, n ∈ I
(B) 2nπ ± π/3, n ∈ I
(C) 2nπ ± π/3, 2mπ ± π/3, m,n ∈ I
(D) nπ ± π/3, n ∈ I
(ii) The general solution of the equation tan²θ + cot²θ = 2 is given by
(A) 2nπ ± π/4, n ∈ I
(B) nπ ± π/4, n ∈ I
(C) nπ + π/4, n ∈ I
(D) none of these
(iii) The general solution of the equation 3tan²θ – 2sin θ = 0 is
(A) nπ, mπ + (-1)ⁿπ/6, m, n ∈ I
(B) nπ + (-1)ⁿπ/6, n ∈ I
(C) nπ, n ∈ I
(D) nπ + (-1)ⁿπ/3, n ∈ I
Exercise 1 Answers:
(i) C
(ii) B
(iii) A
Formulae and Concepts at a Glance
- While solving simultaneous equations, after getting the principle solution add 2nπ to get the general solution.
- While handling problems of trigonometric inequalities, graphical method of solution is very helpful. After getting the principle range add 2nπ to both extremes to get the general solution.
- While solving a trigonometric equation, squaring the equation at any step should be avoided as far as possible. If squaring is necessary, check the solution for extraneous roots.
- Never cancel terms containing unknown terms on the two sides, which are in product. It may cause loss of genuine solution.
- Check that denominator is not zero at any stage while solving equations.
- While solving trigonometric equations, you may get same set of solution repeated in your answer it is necessary for you to exclude those repetitions.
- Some times the two solution set consist partly of common values. In all such cases the common part must be presented only once.
Solved Examples
1. The general solution of the trigonometric equation sin x + cos x = 1, for n = 0, 1, 2,… is given by
(A) x = 2nπ
(B) x = 2nπ + π/2
(C) x = nπ + (-1)ⁿ(π/4) - π/4
(D) none of these
Solution: We write the given equation as
(1/√2)sin x + (1/√2)cos x = 1/√2
or cos(π/4) sin x + sin (π/4) cos x = sin (π/4) or sin (x + π/4) = sin (π/4)
⟹ x + π/4 = nπ + (-1)ⁿ(π/4)
or x = nπ + (-1)ⁿ(π/4) - (π/4) when n = 0, 1, 2,…
2. The number of all possible triplets (a₁, a₂, a₃) such that a₁ + a₂ cos 2x + a₃ sin² x = 0 for all x is
(A) zero
(B) one
(C) three
(D) infinite
Solution: (D) We write the given relation as
a₁ + a₂cos2x + a₃(1 - cos2x)/2 = 0
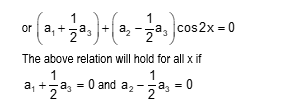
Choosing a₃ = k, k∈ℝ, we get, a₁ = -k/2, a₂ = k/2.
Hence the solution set is (-k/2, k/2, k), where k is any real number. Thus the number of solutions is infinite.
3. The solution set of (2cos x - 1) (3 + 2cos x) = 0 in the interval 0 ≤ x ≤ 2π is
(A) {π/3}
(B) {π/3, 5π/3}
(C) {π/3, 5π/3, cos⁻¹(-3/2)}
(D) none of these
Solution: (B) We have 2cos x - 1 = 0 or 3 + 2cos x = 0
But 3 + 2cos x = 0 gives cos x = -3/2 which is not possible.
From 2cos x - 1 = 0, we get cos x = 1/2 whence x = π/3, 2π - π/3 i.e. 5π/3 in the interval 0 ≤ x ≤ 2π.
Thus the solution set in the given interval is {π/3, 5π/3}.