Logarithm & properties

If a > 0 and a ≠ 1, then logarithm of a positive number m is defined as the index x of that power of 'a' which equals m i.e. log_am = x iff a^x = m
a^log_am = m ......(1)

The function defined by f(x) = log_ax, a > 0, a ≠ 1 is called logarithmic function. Its domain is (0, ∞) and range is ℝ.

When base is 'e' then the logarithmic function is called natural logarithmic function and when base is 10, then it is called common logarithmic function.

Graph of logarithmic functions

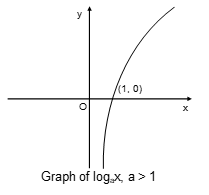
y = log_ax, a > 1

(i) When 0 < x < 1:

x = a^y.

That is, we have to choose those values of y for which 0 < a^y < 1.

Since a > 1, y ≤ 0 ⟹ y ∈ (-∞, 0).

(ii) When x = 1:

x = a^y.

We have to choose that value of y for which x becomes 1 ⟹ y = 0.

(iii) When x > 1:
x = a^y.

We have to choose those values of y for which x > 1.

Since a > 1, 0 < y < ∞.

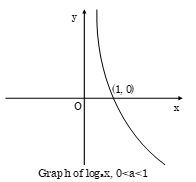
y = log_ax, 0 < a < 1

(iv) When 0 < x < 1:

we have to choose those values of y for which 0 < a^y < 1.

Since 0 < a < 1, y > 0.

(v) When x > 1:

we have to choose those values of y for which a^y > 1.

Since a < 1, y < 0.

Graph of log_a|x|:

log_a|x| is an even function. Hence its graph will be symmetrical about the y-axis.

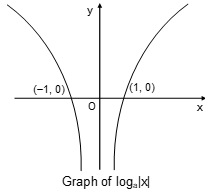
Graph of log_a|x|

Properties of Logarithmic Functions

(i) log_ax₁ + log_ax₂ + .... + log_ax_n = log_a(x₁x₂ ....x_n).

(ii) log_ax₁ - log_ax₂ = log_a(x₁/x₂).

(iii) log_a^mx = (1/m)log_ax.

(iv) log_axⁿ = (n/m)log_ax.

Changing the Base

log_ba = log_ca / log_cb

In general:

log_ba = log_ca × log_dc × log_ed × ... × log_bk

Also log_ca = (log_ba)/(log_bc)

log_aa = (log_ba)/(log_ba) = 1

and log_ba = 1/(log_ab)

Remark: Any real number n > 0 can be written as n = a^log_an.

Inequalities in logarithm

Let log_ap > log_aq.

Let us assume that x = log_ap ⟹ p = a^x

and y = log_aq ⟹ q = a^y.

Let x > y.

If a > 1

then a^x > a^y ⟹ p > q.

If 0 < a < 1,

a^x < a^y ⟹ p < q.

Key Points for Inequalities

• If a > 1, p > 1, then log_ap > 0.
• If 0 < a < 1, p > 1 ⟹ log_ap < 0.
• If a > 1, 0 < p < 1 ⟹ log_ap < 0.
• If p > a > 1 ⟹ log_ap > 1.
• If a > p > 1 ⟹ 0 < log_ap < 1.
• If 0 < a < p < 1 ⟹ 0 < log_ap < 1.
• If 0 < p < a < 1 ⟹ log_ap > 1.

Illustration 1: The value of (0.16)^{log_2.5(1/3) + (1/3)-∞} is equal to

(A) 4

(B) 5

(C) 6

(D) 7

Solution (A):

Let A = (0.16)^{log_2.5(1/3) + (1/3)-∞} = (0.4)^{2log_2.5(1/2)}

= (2/5)^log_2.5(1/2) = (2/5)^log_5/2(1/2)

= (2/5)^log_5/2(1/2) = (5/2)^log_5/24 = 4.

Illustration 2: If ln2. log_b625 = log₁₀16. ln10, then the value of b is

(A) 4

(B) 5

(C) 6

(D) 7

Solution (B):

We have ln2. log_b5⁴ = log₁₀2⁴. ln10

⟹ 4 ln2. log_b5 = 4log₁₀2. ln10

⟹ ln2. log_b5 = (ln2/ln10). ln10

⟹ log_b5 = 1 ⟹ b = 5.

Exercise 1

Ques. If log_ax, log_bx, log_cx are in A.P. where x ≠ 1, then

(A) a² = (bc)^log_ba

(B) c² = (ac)^log_ab

(C) b² = (ac)^log_cb

(D) none of these

Ques. If n is a natural number such that n = p₁^a₁ · p₂^a₂ · p₃^a₃ ......p_k^a_k where p₁, p₂, p₃, …., p_k are distinct prime numbers, then

(A) log n > k log 2

(B) log n < k log 2

(C) k log n > log 2

(D) k log n < log 2

Ques. The value of x satisfying |x-1|^{log₃x²-2log₃9} = (x-1)⁷ is/are

(A) 27

(B) 4

(C) 2, 81

(D) none of these

Ques. x^{log y - log z} · y^{log z - log x} · z^{log x - log y} is equal to

(A) log x

(B) log y

(C) 0

(D) 1

Ques. If log₃ 2, log₃ (2x – 5), log₃ (2x – 7/2) are in A.P., then x is equal to

(A) 3

(B) 4

(C) 5

(D) 6

Answer to Exercises

(i) B

(ii) A

(iii) C

(iv) D

(v) A

Formulae

• a^log_am = m
• When base is e, then logarithmic function is called natural logarithmic function and when base is 10, then it is called common logarithmic function.
• log_axⁿ = (n/m)log_ax
• log_ca = (log_ba)/(log_bc)
• log_ap > log_aq

1. p > q if a > 1
2. p < q if 0 < a < 1

• Graph of log_ax shows different behaviors for a > 1 and 0 < a < 1

Solved Examples

Problem 1: If log₄5 = a and log₅6 = b, then log₃2 is equal to

(A) 1/(2a+1)

(B) 1/(2b+1)

(C) 2ab + 1

(D) 1/(2ab+1)

Solution (D): 4ᵃ = 5; 5ᵇ = 6 ⟹ (4ᵃ)ᵇ = 6; ⟹ 2²ᵃᵇ = 2¹·3; 2²ᵃᵇ⁻¹ = 3

(2ab - 1) log₂2 = log₂3 ⟹ log₃2 = 1/(2ab+1).

Problem 2: The value of log₃4 log₄5 log₅6 log₆7 log₇8 log₈9 is

(A) 1

(B) 2

(C) 3

(D) 4

Solution (B): log₃4 log₄5 = log₃5; log₅6 log₆7 = log₅7; log₇8 log₈9 = log₇9

⟹ given expression = log₃5 log₅7 log₇9 = log₃9 = 2.

Problem 3: If a = log₂₄12, b = log₃₆24 and c = log₄₈36, then 1 + abc is equal to

(A) 2ab

(B) 2ac

(C) 2bc

(D) 0

Solution (C): 1 + abc = 1 + log₂₄12 log₃₆24 log₄₈36 = 1 + log₄₈12

= log₄₈48 + log₄₈12 = log₄₈(48 × 12) = log₄₈(24)² = 2log₄₈24 = 2log₄₈36 log₃₆24 = 2bc.

Problem 4: If log x : log y : log z = (y - z) : (z - x) : (x - y), then

(A) xᵗ·yᶻ·zˣ = 1

(B) xˣ yʸ zᶻ = 1

(C) xˣ⁺ʸ yʸ⁺ᶻ zᶻ⁺ˣ = 1

(D) none of these

Solution (B): (log x)/(y-z) = (log y)/(z-x) = (log z)/(x-y) = k

⟹ x log x + y log y + z log z = k[x(y-z) + y(z-x) + z(x-y)] = 0

⟹ log xˣ + log yʸ + log zᶻ = 0 ⟹ xˣ · yʸ · zᶻ = 1.

Problem 5: x^{log_xy + log_yz} is equal to

(A) x

(B) y

(C) z

(D) none of these

Solution (C): Given expression = x^log_xz = z.

Problem 6: The sum of the series 1/log_a2 + 1/log_a4 + 1/log_a8 + ..... upto n terms is

(A) n(n+1)/(2 log_a2)

(B) n/(2 log_a2)

(C) (n+1)/(2 log_a2)

(D) n(n+1)(2n+1)/(6 log_a2)

Solution (A): The given expression can be written as log_a2 + log_a4 + log_a8 + .... upto n terms = log_a2 + 2 log_a2 + 3 log_a2 + .... n log_a2 = log_a2 [1+ 2 + ... n] = (n(n+1))/(2) log_a2.

Problem 7: The value of 'b' satisfying log_√b b = 3⅓ is

(A) 30

(B) 31

(C) 32

(D) 33

Solution (C): We have log_√b b = 3⅓ ⟹ log_b^(1/2) b = 10/3

⟹ (2/3) log_b b = 10/3 ⟹ log₂b = 5

⟹ b = 2⁵.

Problem 8: The value of x, satisfying log_a(1 + log_b{1 + log_c(1 + log_px)}) = 0, is

(A) 4

(B) 3

(C) 2

(D) 1

Solution (D): The given equation yields 1 + log_b{1 + log_c(1 + log_px)} = 1

⟹ log_b{1 + log_c(1 + log_px)} = 0

⟹ 1 + log_c(1 + log_px) = 1

⟹ log_c(1 + log_px) = 0

⟹ 1 + log_px = 1

⟹ log_px = 0

⟹ x = 1.

Problem 9: For 0 < x < 1, the value of log(1 + x) + log(1 + x²) + .... to ∞ is

(A) log(1 - x)

(B) -log(1 - x)

(C) log x

(D) -log x

Solution (B): The given expression = log [(1 + x) (1 + x²) ..... to ∞ ]

= log[ 1+ x + x² + x³ + .... to ∞ ]

= log(1/(1-x))

= -log(1 - x).

Problem 10: The value of x satisfying 18^4x-3 = (54√2)^3x-4 is

(A) 2

(B) 6

(C) 3

(D) 4

Solution (B): Here 18^4x-3 = (54√2)^3x-4.

Taking log on both sides, we get

(4x - 3) log18 = (3x - 4) log(54√2)/2

⟹ (4x - 3) log18 = (3x - 4) log(18)^(3/2)

⟹ (4x - 3) = (3x - 4). 3/2

⟹ x = 6.

Assignment Problems

Ques 1. The value of x, satisfying the inequality log₀.₃(x² + 8) > log₀.₃9x, lies in

(A) 1 < x < 8

(B) 8 < x < 13

(C) x > 8

(D) none these

Ques 2. The value of x, satisfying 3^-log₃(x+1) = 2^{-log₂x + 3}, is

(A) x = 0

(B) x = 1

(C) x = 2

(D) x = 3

Ques 3. Values of x satisfying the equation log₍₂ₓ₋₃₎(6x² + 23x + 21) = 4 - log₍₃ₓ₊₇₎(4x² + 12x + 9)

(A) 1/3

(B) 1/4

(C) 1/5

(D) 1/6

Ques 4. Value of x, satisfying the equation (6/5)ᵃ^{log₁₀x + log₁₀a·log₅5} = 3^{log₁₀(x/10)} = 9^{log₁₀x+log₁₀2} is

(A) 50

(B) 100

(C) 150

(D) 200

Ques 5. 1/log₂n + 1/log₃n + 1/log₄n +....... + 1/log₄₃n is equal to

(A) log n/log(43!)

(B) 1/log₄₃!n

(C) log₄₃! n

(D) none of these

Ques 6. The value of x, satisfying the equation log₁₀(98 + √x³ - x² - 12x + 36) = 2 is

(A) -3

(B) -4

(C) -5

(D) -6

Ques 7. If x > 1, y > 1, z > 1 are in G.P, then 1/(1+ln x), 1/(1+ln y), 1/(1+ln z) are in

(A) A.P

(B) G.P

(C) H.P

(D) none of these

Ques 8. log₃(log₂(log√₆ 81)) + 3 is equal to

(A) 2

(B) 1

(C) 3

(D) none of these

Ques 9. log₃ log₂ log₅ 625 is equal to

(A) log₂3

(B) 1

(C) log₃2

(D) 0

Ques 10. If a, b, c are in G.P., then log_ax, log_bx, log_cx are in

(A) A.P.

(B) G.P.

(C) H.P.

(D) none of these

Ques 11. log₁₀ tan1° + log₁₀ tan 2° + … + log₁₀tan 89° is

(A) tan1°

(B) tan 45°

(C) 0

(D) ∞

Ques 12. log tan1°, log tan2°, log tan3° … log tan89° is

(A) 1

(B) 0

(C) 2

(D) none of these

Ques 13. log_ba log_cb log_ac is equal to

(A) 0

(B) 1

(C) log_a abc

(D) 10

Ques 14. If (log a)/(b-c) = (log b)/(c-a) = (log c)/(a-c), then a^b+c. b^c+a . c^a+b is equal to

(A) 0

(B) abc

(C) 1

(D) none of these

Ques 15. If log₅ log₅(√x + 5 + √x) = 0.7 + 5, then x is

(A) 3

(B) 4

(C) 5

(D) 6

Answer to Assignment

1. A

2. B

3. B

4. B

5. B

6. B

7. C

8. B

9. B

10. C

11. B

12. B

13. B

14. C

15. B