The eccentricity e of a hyperbola is always greater than 1 and is given by e = sqrt(1 + b 2 / a 2 ). Higher eccentricity indicates a more “stretched” curve.

Asymptotes are lines that the branches approach at infinity. For (x 2 / a 2 ) - (y 2 / b 2 ) = 1, the asymptotes are y = (b/a) x and y = -(b/a) x.

CBSE Class 12 Maths Notes on Hyperbola – Standard Equation, Asymptotes & Properties

Q: A hyperbola is the locus of points for which the absolute difference of distances from two fixed points (called foci) is constant. It consists of two mirror-image branches.

A hyperbola is the locus of points for which the absolute difference of distances from two fixed points (called foci) is constant. It consists of two mirror-image branches.

Q: For a hyperbola centered at the origin with transverse axis along the x-axis, the standard form is (x^2 / a^2) - (y^2 / b^2) = 1, where a is the semi-transverse axis and b is the semi-conjugate axis.

For a hyperbola centered at the origin with transverse axis along the x-axis, the standard form is (x^2 / a^2) - (y^2 / b^2) = 1, where a is the semi-transverse axis and b is the semi-conjugate axis.

Q: The latus rectum is a chord through a focus perpendicular to the transverse axis. Its length is 2 b 2 / a for the standard form (x 2 / a 2 ) - (y 2 / b 2 ) = 1.

The latus rectum is a chord through a focus perpendicular to the transverse axis. Its length is 2 b 2 / a for the standard form (x 2 / a 2 ) - (y 2 / b 2 ) = 1.

Equation of Hyperbola in Standard Form

Standard Form: x²/a² - y²/a²(e² - 1) = 1

where a²(e² - 1) = b²

Some Terms Related to Hyperbola

Standard Equation: x²/a² - y²/b² = 1

Centre: C ≡ (0, 0)
Foci: S(ae, 0) and S'(-ae, 0)
Directrices: x = a/e and x = -a/e
Vertices: A(a, 0) and A'(-a, 0)
Axes: The straight line joining the vertices at A and A' is called the transverse axis of the hyperbola and its length AA' is 2a.
Latus Rectum: Since the latus rectum is the chord through a focus at right angle to the transverse axis, length of latus rectum = 2b²/a

Illustration 1:

Problem: In the hyperbola 4x² - 9y² = 36, the eccentricity is

(A) √13/4 (B) √13/3 (C) √13/4 (D) √13/5

Solution (B):

The equation to the hyperbola is given as x²/9 - y²/4 = 1 ...(1)

Comparing with the standard equation x²/a² - y²/b² = 1 ...(2)

We find a² = 9, b² = 4, where a = 3, b = 2

e = √(1 + b²/a²) = √(1 + 4/9) = √(13/9) = √13/3

Conjugate Hyperbola

The hyperbola, whose transverse and conjugate axes are respectively the conjugate and transverse axes of a given hyperbola, is called the conjugate hyperbola of the given hyperbola, and the two hyperbolas are conjugate to one another.

Conjugate Hyperbolas:

x²/a² - y²/b² = 1 and -x²/a² + y²/b² = 1

For the conjugate hyperbola -x²/a² + y²/b² = 1:

a² = b²(e² - 1), its vertices are (0, ±b)
Directrices are y = ±b/e

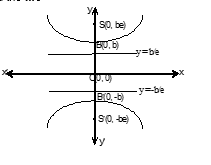
Conjugate Hyperbola

Diagram Description: A coordinate system showing both the original hyperbola and its conjugate, with vertices at (0, b) and (0, -b), foci at (0, be) and (0, -be), and directrices at y = ±b/e

Note: If the centre of hyperbola is (h, k) and axes are parallel to the co-ordinate axes, then its equation is (x-h)²/a² - (y-k)²/b² = 1. By shifting the origin at (h, k) without rotating the co-ordinate axes, the above equation reduces to X²/a² - Y²/b² = 1, where x = X + h, y = Y + k.

Difference between Hyperbola and Conjugate Hyperbola

Property	Hyperbola (x²/a² - y²/b² = 1)	Conjugate Hyperbola (-x²/a² + y²/b² = 1)
Centre	(0, 0)	(0, 0)
Vertices	(±a, 0)	(0, ±b)
Length of Transverse Axis	2a	2b
Length of Conjugate Axis	2b	2a
Foci	(±ae, 0)	(0, ±be)
Equation of directrices	x = ±a/e	y = ±b/e
Relation in a, b and e	b² = a²(e² - 1)	a² = b²(e² - 1)
Length of Latus Rectum	2b²/a	2a²/b
Distance between foci	2ae	2be
Distance between directrices	2a/e	2b/e
Focal radii	SP = ex₁ - a & S'P = ex₁ + a	SP = ey₁ - b & S'P = ey₁ + b
Difference of Focal radii	2a	2b

Illustration 2:

Problem: If e₁ and e₂ are the eccentricities of the hyperbola x²/a² - y²/b² = 1 and its conjugate hyperbola, the value of e₁⁻² + e₂⁻² is

(A) 2 (B) 0 (C) 1 (D) 3

Solution (C):

The eccentricity e₁ of the given hyperbola is obtained from b² = a²(e₁² - 1) ...(1)

The eccentricity e₂ of the conjugate hyperbola is given by a² = b²(e₂² - 1) ...(2)

Multiply (1) and (2). We get 1 = (e₁² - 1)(e₂² - 1)

⇒ 0 = e₁²e₂² - e₁² - e₂² + 1 ⇒ e₁⁻² + e₂⁻² = 1

Relative Position of a Point with Respect to the Hyperbola

The quantity x₁²/a² - y₁²/b² - 1 is positive, zero or negative, according as the point (x₁, y₁) lies within, upon or without the curve.

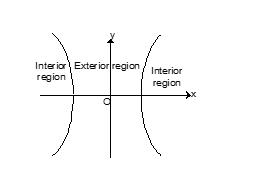
Diagram Description: A coordinate system showing a hyperbola with interior regions (between the two branches) and exterior regions (outside the hyperbola branches)

Parametric Coordinates

The coordinates of a point of the hyperbola x²/a² - y²/b² = 1 can be expressed in terms of a single parameter, say θ.

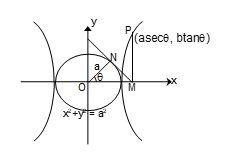
Parametric

Parametric Form:

x = a sec θ, y = b tan θ

In the adjacent figure OM = a sec θ and PM = b tan θ. Thus any point on the curve, in parametric form is (a sec θ, b tan θ)

Equation of Tangent

Point Form: The tangent at any point (x₁, y₁) on the curve is xx₁/a² - yy₁/b² = 1
Parametric Form: The tangent at the point 'θ' is (x sec θ)/a - (y tan θ)/b = 1
Slope Form: The straight line y = mx + c is a tangent to the curve, if c² = a²m² - b². In other words, y = mx ± √(a²m² - b²) touches the curve, for all those values of m when m > b/a or m < -b/a.

Equation of Normal

Point Form: Equation of the normal at any point (x₁, y₁) to the curve is (x - x₁)/(x₁/a²) = (y - y₁)/(-y₁/b²)
Parametric Form: The equation of the normal at θ is ax cos θ + by cot θ = a² + b²

Director Circle

Equation of director circle is x² + y² = a² - b². That means if a² > b², there would exist several points such that tangents drawn from them would be mutually perpendicular. If a² < b², no such point exist. For a² = b², centre is the only point from which two perpendicular tangents to the hyperbola can be drawn.

Chord of Contact

Chord of contact of point (x₁, y₁) w.r.t. hyperbola x²/a² - y²/b² = 1 is:

xx₁/a² - yy₁/b² = 1

Equation of Polar of a Point

Equation of polar of point (x₁, y₁) w.r.t. hyperbola x²/a² - y²/b² = 1 is:

xx₁/a² - yy₁/b² = 1

Pole of a Line

Pole of a given line lx + my + n = 0 w.r.t. hyperbola x²/a² - y²/b² = 1 is:

(-a²l/n, b²m/n)

Illustration 3:

Problem: The line x cos α + y sin α = p touches the hyperbola x²/a² - y²/b² = 1 if

(A) a² cos² α + b² sin² α = p² (B) a² cos² α + b² tan² α = p²

Solution (D):

The given line is x cos α + y sin α = p

⇒ y sin α = -x cos α + p ⇒ y = -x cot α + p cosec α

Comparing this line with y = mx + c; m = -cot α, c = p cosec α

Since the given line touches the hyperbola x²/a² - y²/b² = 1 then c² = a²m² - b²

p² cosec² α = a² cot² α - b²; or, p² = a² cos² α - b² sin² α

Asymptote

The straight line, to which the tangent to a curve tends as the point of contact tends to approach infinity, is called an asymptote of the curve. In other words, an asymptotes tends to touch the curve at infinity.

Asymptote of a curve may also be defined in another way - A straight line that touches the given curve at infinity but the line itself is not at infinity is called an asymptote to the given curve.

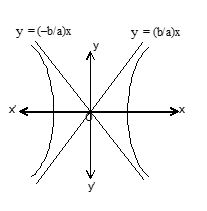
Asymptote

For the hyperbola x²/a² - y²/b² = 1, the equations of the asymptotes are:

x/a ± y/b = 0

So, there are two asymptotes both passing through the centre and equal inclined to the axis of x the inclination being tan⁻¹(b/a).

The angle between two asymptotes is 2 tan⁻¹(b/a).

Diagram Description: A coordinate system showing a hyperbola with its two asymptotes y = (b/a)x and y = -(b/a)x passing through the origin

Rectangular Hyperbola

A hyperbola whose asymptotes are at right angles to each other is called a rectangular hyperbola.

Illustration 4:

Problem: The equation of pair of asymptotes of the hyperbola 3x² - 5xy - 2y² + 5x + 11y - 8 = 0 is

(A) 3x² - 5xy - 2y² + 5x + 11y + 13 = 0 (B) 3x² - 5xy - 2y² + 5x + 11y - 1 = 0

Solution (D):

Given hyperbola is 3x² - 5xy - 2y² + 5x + 11y - 8 = 0

Since, the equation to the asymptotes only differs from it by a constant, it must be of the form 3x² - 5xy - 2y² + 5x + 11y + c = 0

For pair of straight lines the condition is abc + 2fgh - af² - bg² - ch² = 0

Here a = 3, b = -2, h = -5/2, g = 5/2, f = 11/2, c = c

Solving: c = -12

∴ Required equation is 3x² - 5xy - 2y² + 5x + 11y - 12 = 0

Exercise:

The equation of hyperbola of given transverse axis whose vertex bisects the distance between centre and the focus is
(A) 3x² + y² = 3a² (B) x² - y² = 3a² (C) 3x² - y² = 3a² (D) none of these
If the line y = mx + √(a²m² - b²) touches the hyperbola x²/a² - y²/b² = 1 at the point (a sec φ, b tan φ), then the value of φ is
(A) tan⁻¹(b/am) (B) cos⁻¹(a²/x₁) (C) cot⁻¹(b/am) (D) sin⁻¹(b/am)
The locus of the foot of perpendicular from the centre upon any normal to the hyperbola x²/a² - y²/b² = 1 is
(A) (x² + y²)(a²y² + b²x²) = (a² + b²)²x²y²

(B) (x² + y²)(a²y² - b²x²) = (a² + b²)²x²y²

(C) (x² - y²)(a²y² + b²x²) = (a² + b²)²x²y²

(D) y²/b² = (1/4)(1 - 1/t²)

Exercise:

The equation of the conjugate hyperbola of the hyperbola x² - 5xy - 2y² + 5x + 11y - 8 = 0 is
(A) 3x² - 5xy - 2y² + 5x + 11y = 0 (B) 3x² - 5xy - 2y² + 5x + 11y - 12 = 0

(C) 3x² - 5xy - 2y² + 5x + 11y - 10 = 0 (D) 3x² - 5xy - 2y² + 5x + 11y + 21 = 0
The asymptotes of the hyperbola 2x² + 5xy + 2y² + 4x + 5y = 0 is
(A) x + 2y + 1 = 0, 2x + y + 2 = 0 (B) x - 2y + 1 = 0, 2x - y + 2 = 0

(C) x + 2y + 20 = 0, 2x + y + 5 = 0 (D) none of these

Answer to Exercises

Exercise 1: (i) C (ii) D (iii) B
Exercise 2: (i) B (ii) A

Formulae and Concepts at a Glance

For the hyperbola x²/a² - y²/b² = 1, the eccentricity is √(a² + b²)/a > 1 and the foci are (±ae, 0).
Length of the transverse axis is 2a and that of the conjugate axis 2b with latus rectum = 2b²/a and distance between the directrices = 2a/e.
Equation of the tangent at the point (x₁, y₁) is xx₁/a² - yy₁/b² = 1.
Equation of the normal at the point (x₁, y₁) is a²x/x₁ + b²y/y₁ = a² + b².
The line y = mx + c touches the hyperbola x²/a² - y²/b² = 1 for c² = a²m² - b².
Two perpendicular tangents to the hyperbola x²/a² - y²/b² = 1 intersect on its director circle x² + y² = a² - b².
Parametric equation of the hyperbola x²/a² - y²/b² = 1 are x = a sec θ, y = b tan θ.
Condition for the parabola to be rectangular is that a = b ⇒ e = √2. Equation becomes x² - y² = a².
Equation of the hyperbola conjugate to the hyperbola x²/a² - y²/b² = 1 is -x²/a² + y²/b² = 1 (parametric equations x = a tan θ, y = b sec θ).
Equation of the asymptotes are y = ±(b/a)x.

Solved Examples

1. The eccentricity of the conic represented by x² - y² - 4x + 4y + 16 = 0 is

(A) 1 (B) √2 (C) 2 (D) 1/2

Solution (B):

We have x² - y² - 4x + 4y + 16 = 0

or, (x² - 4x) - (y² - 4y) = -16

or, (x² - 4x + 4) - (y² - 4y + 4) = -16

or (x - 2)² - (y - 2)² = -16 or, -(x-2)²/4² + (y-2)²/4² = 1

Shifting the origin at (2, 2), we obtain -X²/4² + Y²/4² = 1, where x = X + 2, y = Y + 2

This is a rectangular hyperbola, whose eccentricity is always √2.

2. If m is a variable, the locus of the point of intersection of the lines x/3 - y/2 = m and x/3 + y/2 = 1/m is a/an

(A) parabola (B) ellipse (C) hyperbola (D) none of these

Solution (C):

The required locus is obtained by eliminating the variable m from the given equations of the lines. Then we have (x/3 - y/2)(x/3 + y/2) = m × (1/m) = 1

⇒ x²/9 - y²/4 = 1

This is clearly a hyperbola.

3. P is a point on the hyperbola x²/a² - y²/b² = 1, N is the foot of the perpendicular from P on the transverse axis. The tangent to the hyperbola at P meets the transverse axis at T. If O is the centre of the hyperbola, then TO.ON is equal to

(A) e² (B) a² (C) b² (D) b²/a²

Solution (B):

Let P(x₁, y₁) be a point on the hyperbola. Then the coordinates of N are (x₁, 0).

The equation of the tangent at (x₁, y₁) is xx₁/a² - yy₁/b² = 1

This meets x-axis at T(a²/x₁, 0)

∴ TO.ON = (a²/x₁) × x₁ = a²

Assignment

The curve represented by x = ae^θ, y = be^(-θ), θ ∈ R is

(A) a hyperbola (B) an ellipse (C) a parabola (D) a circle
Eccentricity of the hyperbola whose asymptotes are given by 3x + 2y - 5 = 0 and 2x - 3y - 5 = 0 is

(A) √2 (B) 3/2 (C) 2 (D) none of these
The reciprocal of the eccentricity of rectangular hyperbola, is

(A) 2 (B) 1/2 (C) √2 (D) 1/√2
The angle between the asymptotes of the hyperbola 24x² - 8y² = 27 is

(A) 90° (B) 60° (C) 45° (D) 30°
Through the positive vertex of the hyperbola x²/a² - y²/b² = 1 a tangent is drawn, where does it meet the conjugate hyperbola

(A) at the points (a², b) (B) at the points (0, 0)

(C) at the points (a, b) (D) at the points (a, b²)
The co-ordinates of a point are a tan(θ + α) and b tan(θ + β) where θ is variable, then the locus of the point is a

(A) circle (B) hyperbola (C) parabola (D) ellipse
If normal to the hyperbola xy = c² at point 't' meets the curve again at a point 't₁' then t³t₁ is equal to

(A) 1 (B) 0 (C) 2 (D) -1
The relative position of (2, 3) with respect to the hyperbola 9x² - 8y² - 18x + 9 = 0 is

(A) within the hyperbola (B) outside the hyperbola

(C) on the hyperbola (D) none of these
The point of intersection of the curves whose parametric equations are x = t² + 1, y = 2t and x = 2s, y = 2/s, is given by

(A) (1, -3) (B) (2, 2) (C) (-2, 4) (D) (1, 2)
If e is the eccentricity of x²/a² - y²/b² = 1 and 'θ' be the angle between the asymptotes, then cos(θ/2) is equal to,

(A) 1/2 (B) 1/e (C) 1/e² (D) none of these
Number of points outside the hyperbola x²/25 - y²/36 = 1 from where two perpendicular tangents can be drawn to the hyperbola are

(A) 0 (B) 1 (C) 2 (D) 3
The rectangular hyperbola xy = 1 cuts the circle x² + y² = 1 at four points. The sum of abscissa of these points is

(A) 1 (B) 0 (C) 2 (D) none of these
e₁ and e₂ are the eccentricities of the hyperbolas xy = c² and x² - y² = c², then e₁² + e₂² =

(A) 1 (B) 4 (C) 8 (D) 6
If the line ax + by + c = 0 is a normal to the curve xy = 1, then

(A) a > 0, b > 0 (B) a > 0, b < 0 or a < 0, b > 0

(C) a < 0, b < 0 (D) none of these
Let P be a point on the hyperbola x² - y² = a² where a is a parameter, such that P is nearest to the line y = 2x. Then the locus of P is
(A) y + x = 0 (B) 2y - 3x = 0 (C) x + 2y + 3 = 0 (D) 2y - x = 0

Answers to Assignment

1. A	2. A	3. D	4. B	5. D
6. B	7. A	8. B	9. B	10. D
11. A	12. B	13. B	14. B	15. D

Frequently Asked Questions

A hyperbola is the locus of points for which the absolute difference of distances from two fixed points (called foci) is constant. It consists of two mirror-image branches.

For a hyperbola centered at the origin with transverse axis along the x-axis, the standard form is (x^2 / a^2) - (y^2 / b^2) = 1, where a is the semi-transverse axis and b is the semi-conjugate axis.

The eccentricity e of a hyperbola is always greater than 1 and is given by e = sqrt(1 + b² / a²). Higher eccentricity indicates a more “stretched” curve.

Asymptotes are lines that the branches approach at infinity. For (x² / a²) - (y² / b²) = 1, the asymptotes are y = (b/a) x and y = -(b/a) x.

The latus rectum is a chord through a focus perpendicular to the transverse axis. Its length is 2 b² / a for the standard form (x² / a²) - (y² / b²) = 1.

S.no	Formulas List
1.	Trigonometric equations
2.	Solution of the triangle
3.	Height and distance
4.	Inverse trigonometric function
5.	Exponential and logarithm series
6.	Logarithm & properties
7.	Quadratic equations
8.	Indefinite integral
9.	Definite integrals
10.	Differential equation

Hyperbola