parabola

Standard Equation of a Parabola

Let S be the focus, ZM the directrix and P the moving point. Draw SZ perpendicular from S on the directrix. Then SZ is the axis of the parabola. Now the middle point of SZ, say A, will lie on the locus of P, i.e., AS = AZ. Take A as the origin, the x-axis along AS, and the y-axis along the perpendicular to AS at A, as in the figure.

Let AS = a, so that ZA is also a. Let (x, y) be the coordinates of the moving point P. Then MP = ZN = ZA + AN = a + x. But by definition MP = PS ⇒ MP² = PS².

So that, (a + x)² = (x – a)² + y².

Hence, the equation of parabola is y² = 4ax.

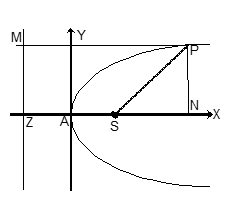
Diagram Description: A coordinate system showing a parabola with focus S at (a, 0), directrix ZM at x = -a, vertex A at origin, and a point P(x, y) on the parabola. The perpendicular from P to the directrix meets it at M, and N is the foot of perpendicular from P to the x-axis.

• Special Cases

Let the vertex be (α, β) and the axis be parallel to the x-axis. Then the equation of the parabola is given by (y – β)² = 4a(x – α), which is equivalent to x = Ay² + By + C.

• Double Ordinate

A chord of parabola which is perpendicular to axis is called the double ordinate.

• Latus Rectum of the Parabola

Double ordinate passing through the focus is called the latus rectum of the parabola.

Length of latus rectum = 4a

Illustration 1: The length of the latus rectum of the parabola 2y² + 3y – 4x – 3 = 0 is

(A) 2

(B) 4

(C) 1

(D) 8

Solution (A):

The given equation can be re-written as

2(y + 3/4)² = 4x + 33/32

which is of the form Y² = 4aX. Length of the latus rectum = 4a = 2.

Exercise 1:

1. The focus of the parabola y² – x – 2y + 2 = 0 is
   (A) (5/2, 1) (B) (5/4, 2) (C) (5/4, 1) (D) none of these
2. A point P on a parabola y² = 4x, the foot of the perpendicular from it upon the directrix, and the focus are the vertices of an equilateral triangle. Then the coordinates of the point P are
   (A) (3, ±√3) (B) (3, ±2√3) (C) (3, ±3√3) (D) none of these

Parametric Equations of a Parabola

Clearly x = at², y = 2at satisfy the equation y² = 4ax for all real values of t. Hence the parametric equations of the parabola y² = 4ax are x = at², y = 2at, where t is the parameter.

Also, (at², 2at) is a point on the parabola y² = 4ax for all real values of t. This point is also described as the point 't' on the parabola.

Focal Distance of any Point

The focal distance of any point P(x, y) on the parabola y² = 4ax is the distance between the point P and the focus S, i.e., PS.

Thus the focal distance = PS = PM = ZN = ZA + AN = a + x

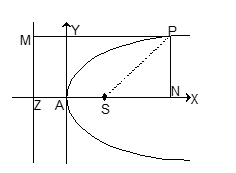
Position of a Point relative to the Parabola

• The condition for P to lie outside the parabola becomes y₁² – 4ax₁ > 0.
• Similarly, the condition for P to lie inside the parabola is y₁² – 4ax₁ < 0.

Illustration 2: The coordinates of a point on the parabola y² = 8x, whose focal distance is 4, are

(A) (1/2, ±2) (B) (1, ±2√2) (C) (2, ±4) (D) none of these

Solution (C):

Focal distance of a point P(x, y) on y² = 4ax is (x + a).

∴ 4 = x + 2 ⇒ x = 2

y² = 8 × 2 = 16 ⇒ y = ±4

Tangent to a Parabola

Tangent at the Point (x₁, y₁)

Let the equation of the parabola be y² = 4ax

yy₁ = 2a(x + x₁)

y = mx + a/m is a tangent to the parabola y² = 4ax, whatever be the value of m.

Thus the point of contact of the tangent y = mx + a/m is (a/m², 2a/m).

Illustration 3: If the line 2x + 3y = 1 touches the parabola y² = 4ax, then the length of the latus rectum is

(A) 4/9 (B) 4/3 (C) 8/3 (D) 8/9

Solution (D):

Equation of any tangent to y² = 4ax is y = mx + a/m ⇒ m²x – my + a = 0

Comparing it with the given tangent 2x + 3y – 1 = 0, we find

m²/2 = -m/3 = a/(-1)

⇒ m = -2/3, a = 2/9

Hence the length of the latus rectum = 4a = 8/9

(Ignoring the negative sign for length).

Chord of Contact

Equation to the chord of contact of the tangents drawn from a point (x₁, y₁), to the parabola y² = 4ax is T = 0, i.e. yy₁ – 2a(x + x₁) = 0.

Equation of a Chord with Midpoint (x₁, y₁):

The equation of the chord of the parabola y² = 4ax with mid point (x₁, y₁) is T = S₁

i.e. yy₁ – 2a(x + x₁) = y₁² – 4ax₁ Or yy₁ – 2ax = y₁² – 2ax₁.

Illustration 4: The equation of the chord of the parabola y² = 12x which is bisected at the point (5, –7) is

(A) 3x – y – 22 = 0 (B) 2x + y – 3 = 0 (C) 6x + 7y + 19 = 0 (D) none of these

Solution (C):

Here (x₁, y₁) = (5, –7) and y² = 12x, a = 3

The equation of the chord is S₁ = T

or y₁² – 4ax₁ = yy₁ – 2a(x + x₁) or (–7)² – 12.5 = y(–7) – 6(x + 5)

⇒ 6x + 7y + 19 = 0.

Exercise 2:

1. A tangent to the parabola y² = 8x makes an angle of 45° with the straight line y = 3x + 5. Then the equation of the tangent is
   (A) x + 2y – 8 = 0 (B) x – 2y + 8 = 0 (C) 3x + 2y + 6 = 0 (D) none of these
2. Any tangent to a parabola y² = 4ax and perpendicular to it from the focus meet on the line
   (A) x = 0 (B) y = 0 (C) x = a (D) y = a
3. Tangents at the extremities of a focal chord of a parabola intersect on
   (A) directrix (B) tangent at vertex (C) axis of parabola (D) none of these

Normal to the Parabola

• Its equation is: y – y₁ = -y₁/2a (x – x₁) ...(i)
• Normal in Terms of m: y = mx – 2am – am³ ...(ii)
• Normal at the Point 't': y = –tx + 2at + at³.

Standard Results for Four Common Forms of Parabola

Property	y² = 4ax	y² = –4ax	x² = 4ay	x² = –4ay
Vertex	(0, 0)	(0, 0)	(0, 0)	(0, 0)
Focus	(a, 0)	(–a, 0)	(0, a)	(0, –a)
Equation of Directrix	x = –a	x = a	y = –a	y = a
Equation of axis	y = 0	y = 0	x = 0	x = 0
Tangent at the vertex	x = 0	x = 0	y = 0	y = 0
Parametric Equation	x = at², y = 2at	x = –at², y = 2at	x = 2at, y = at²	x = 2at, y = –at²
Focal Distance of (x₁, y₁)	x₁ + a	–x₁ + a	y₁ + a	–y₁ + a

Equation of Tangent

Form	y² = 4ax	y² = –4ax	x² = 4ay	x² = –4ay
(a) At the point (x₁, y₁)	yy₁ = 2a(x + x₁)	yy₁ = –2a(x + x₁)	xx₁ = 2a(y + y₁)	xx₁ = –2a(y + y₁)
(b) in terms of m	y = mx + a/m	y = mx – a/m	x = my + a/m	x = my – a/m
(c) in terms of t	yt = x + at²	yt = –x + at²	xt = y + at²	xt = –y + at²

Equation of Normal

Form	y² = 4ax	y² = –4ax	x² = 4ay	x² = –4ay
(a) At the point (x₁, y₁)	y – y₁ = -y₁/2a (x – x₁)	y – y₁ = y₁/2a (x – x₁)	x – x₁ = -x₁/2a (y – y₁)	x – x₁ = x₁/2a (y – y₁)
(b) in terms of m	y = mx – 2am – am³	y = mx + 2am + am³	x = my – 2am – am³	x = my + 2am + am³
(c) in terms of t	y = –tx + 2at + at³	y = tx + 2at + at³	x = –ty + 2at + at³	x = ty + 2at + at³

Exercise 3:

1. The number of distinct normals that can be drawn to the parabola y² = 4x from the point (11/4, 1/4) is
   (A) 1 (B) 2 (C) 3 (D) 4
2. If a normal chord subtends a right angle at the vertex of the parabola y² = 4ax, then it is inclined to the axis at an angle of
   (A) π/2 (B) π/4 (C) tan⁻¹(√3) (D) tan⁻¹(√2)

Answer to Exercises

• Exercise 1: (i) C (ii) B
• Exercise 2: (i) B (ii) A (iii) A
• Exercise 3: (i) B (ii) D

Formulae and Concepts at a Glance

1. The focal distance of any point P(x, y) on y² = 4ax is |x + a|.
2. y = mx + c touches y² = 4ax if c = a/m and the point of contact is (a/m², 2a/m).
3. Parametric equations of the parabola y² = 4ax are x = at², y = 2at.
4. Equation of tangent at 't' is ty = x + at².
5. Equation of normal at 't' is tx + y = at³ + 2at.
6. Equation of the chord joining 't₁' and 't₂' is (t₁ + t₂)y = 2x + 2at₁t₂. This is a focal chord if t₁t₂ = –1.
7. Tangents to y² = 4ax at 't₁' and 't₂' intersect at the point (at₁t₂, a(t₁ + t₂)).

Solved Examples

1. The focus of the parabola x² – 8x + 2y + 7 = 0 is

(A) (0, -1/2) (B) (4, -9/2) (C) (4, 4) (D) (-4, -9/2)

Solution (C):

Given parabola is (x – 4)² = –2(y – 9/2), focus is given by x – 4 = 0, y – 9/2 = -1/2 ⇒ focus is (4, 4).

2. For the parabola y² = 4ax, the ratio of the subtangent to the abscissa is

(A) 1 : 1 (B) 2 : 1 (C) x : y (D) x² : y²

Solution (B):

Sub tangent = y/(dy/dx) & 2yy' = 4a ⇒ y' = 2a/y from y² = 4ax

Sub tangent = 4ax/x = 2ax/x = 2/1.

3. The length of the latus rectum of the parabola x = ay² + by + c is

(A) a/4 (B) a/3 (C) 1/a (D) 1/4a

Solution (C):

x = a(y + b/2a)² + c – b²/4a

or, x – c + b²/4a = a(y + b/2a)²

or, 1/a(x + b²/4a – c) = (y + b/2a)²

∴ the latus rectum = 1/a

4. If a normal chord to the parabola y² = 4x is drawn at (1, 2), then the chord meets the parabola again at

(A) (9, 6) (B) (9, –6) (C) (6, 6) (D) none of these

Solution (B):

For point (1, 2) value of t = 1, the value of t₂ for other end of the normal is t₂ = –1 – 2/1 = –3. So point is (at₂², 2at₂) = (9, –6).

5. If tangents at A and B on the parabola y² = 4ax intersect at the point C, then ordinates of A, C and B are

(A) always in A.P. (B) always in G.P. (C) always in H.P. (D) none of these

Solution (A):

A ≡ (at₁², 2at₁) B ≡ (at₂², 2at₂)

Tangents at A and B will intersect at the point C, whose coordinate is given by (at₁t₂, a(t₁+t₂)) clearly ordinate of A, C and B are always in A.P.

Assignment Questions

1. If the line y – √3x + 3 = 0 cuts the parabola y² = x + 2 at A and B, and if P ≡ (√3, 0), then PA. PB is equal to
   (A) 2(√3 + 2)/3 (B) 4√3/2 (C) 4(2 – √3)/3 (D) 4(2 + √3)/3
2. If (a, b) is the midpoint of a chord passing through the vertex of the parabola y² = 4x, then
   (A) a = 2b (B) 2a = b (C) a² = 2b (D) 2a = b²
3. The chord AB of the parabola y² = 4ax cuts the axis of the parabola at C. If A ≡ (at₁², 2at₁), B ≡ (at₂², 2at₂) and AC : AB = 1 : 3, then
   (A) t₂ = 2t₁ (B) t₁ + 2t₂ = 0 (C) 2t₁ + t₂ = 0 (D) none of these
4. If a chord which is normal to the parabola y² = 4ax at one end subtends a right angle at the vertex, then its slope is
   (A) 1 (B) √3 (C) √2 (D) 2
5. If (x₁, y₁), (x₂, y₂) and (x₃, y₃) be three points on the parabola y² = 4ax the normals at which are concurrent, then y₁ + y₂ + y₃ is equal to
   (A) 2a (B) 0 (C) 4a (D) none of these
6. If the straight line y = mx + c (m > 0) touches the parabola y² = 8(x + 2), then the minimum value taken by c is
   (A) 12 (B) 8 (C) 4 (D) 6
7. The length of the subtangent to the parabola y² = 16x at the point whose abscissa is 4, is
   (A) 2 (B) 4 (C) 8 (D) none of these
8. If the chord y = mx + c subtends a right angle at the vertex of the parabola y² = 4ax, then the value of c is
   (A) –4am (B) 4am (C) –2am (D) 2am
9. If the tangents at P and Q on a parabola meet at T, then SP, ST and SQ are in
   (A) A.P (B) G.P (C) H.P (D) none of these
10. The number of real normals that can be drawn from the point (4, 2) to the parabola y² = 8x is
    (A) 1 (B) 2 (C) 3 (D) none of these
11. If (9, 12) is one end of a double ordinate of the parabola y² = 16x, then its equation is
    (A) x + 9 = 0 (B) y + 9 = 0 (C) y – 9 = 0 (D) x – 9 = 0
12. If two tangents drawn from the point (α, β) to the parabola y² = 4x be such that the slope of one tangent is double of the other, then
    (A) 2α² = 9β (B) 2α = 9β² (C) 2β² = 9α (D) none of these
13. At what point on the parabola y² = 4x the normal makes equal angles with the axes?
    (A) (4, 4) (B) (1, –2) (C) (9, 6) (D) (4, –4)
14. If the segment intercepted by the parabola y² = 4ax with the line lx + my + n = 0 subtends a right angle at the vertex, then
    (A) 4am + n = 0 (B) 4am + 4al + n = 0 (C) 4al + n = 0 (D) al + n = 0
15. The length of a focal chord of the parabola y² = 4ax making an angle θ with the axis of the parabola is
    (A) 4a cosec² θ (B) 4a sec² θ (C) a cosec² θ (D) none of these

Answers to Assignment

1. D	2. D	3. C	4. C	5. B
6. C	7. C	8. A	9. B	10. A
11. D	12. C	13. B	14. C	15. A