vector

Representation of a Vector

We represent a vector by a line segment having a direction. We write it as AB→ or a→, or simply as AB or a. A is called the initial point and B the terminal point of the vector.

The magnitude of the vector is denoted by |AB| or |a| (read as modulus of vector a).

Two vectors are said to be equal if they have (i) the same length, (ii) the same or parallel supports and (iii) the same sense.

Position Vector of a Point

The position vector (p.v.) of any point P, with respect to the origin is the vector OP. For any two points P and Q in space, the equality PQ = OQ – OP.

Unit Vector

A vector having the magnitude as one (unity) is called a unit vector.

Unit vector in the direction of a is defined as a / |a| and is denoted by â (read as a cap).

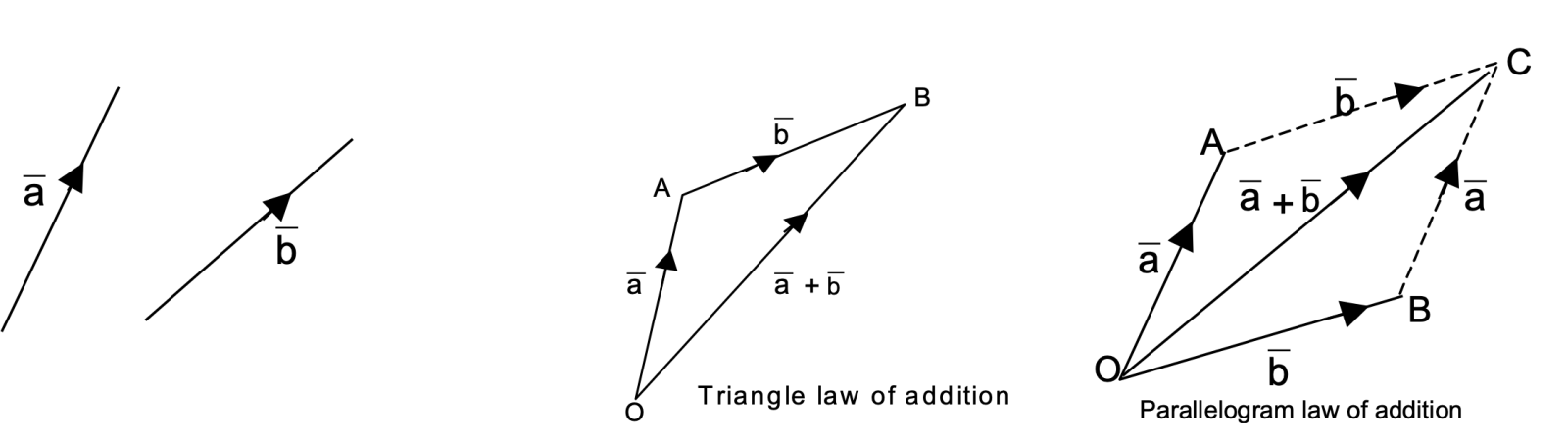
Addition of Vectors

Given two vectors a and b, then their sum or resultant is written as (a + b).

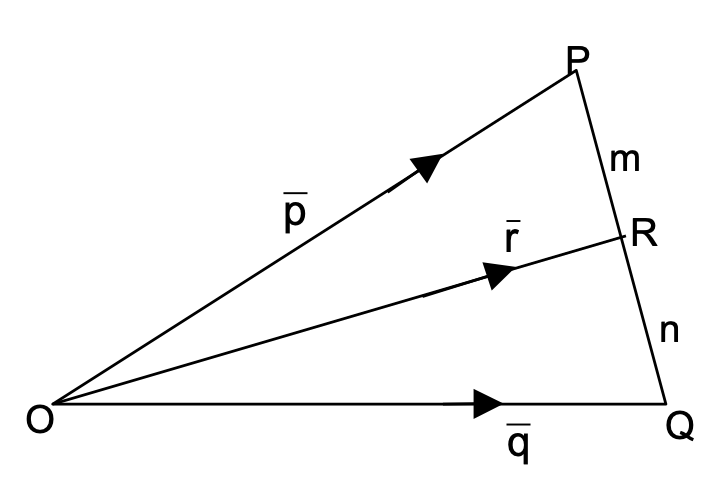
Section Formula

Let the p.v. of a point P be ⃗p and that of another point Q be ⃗q. If the line joining P and Q is divided by a point R in the ratio of m : n (internally or externally), then
⃗r = m⃗q + n⃗p / (m + n)
For internal division take m : n as positive, and for external division take m : n as negative (i.e., either of m or n as negative).

If R is the mid-point of PQ, then ⃗r = ⃗p + ⃗q / 2

If A, B, C are the vertices of a triangle with p.v.’s ⃗a, ⃗b, ⃗c respectively, then the p.v. of the centroid ⃗n of the triangle is given by ⃗g = ⃗a + ⃗b + ⃗c / 3

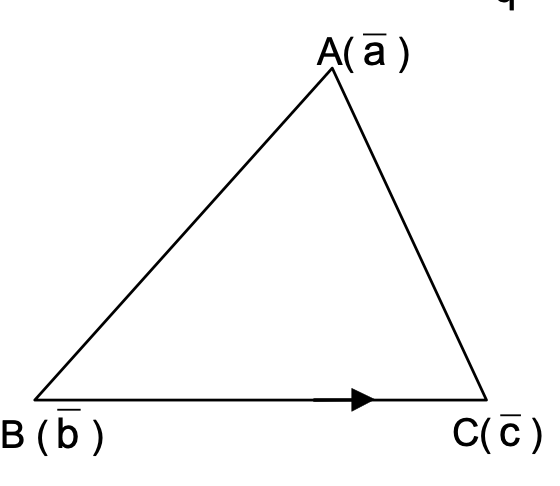
LINEAR COMBINATIONS OF VECTORS

The linear combination of a finite set of vectors ā₁, ā₂, ... āₙ is defined as a vector r̄ such that
r̄ = k₁ā₁ + k₂ā₂ + ...... + kₙāₙ, where k₁, k₂, … kₙ are any scalars (real numbers).

Linearly Dependent and Independent Vectors

A system of vectors ā₁, ā₂, ..., āₙ is said to be linearly dependent if there exists a system of scalars k₁, k₂, ..., kₙ (not all zero) such that
k₁ā₁ + k₂ā₂ + ... + kₙāₙ = Ō.
They are said to be linearly independent if every relation of the type k₁ā₁ + k₂ā₂ + ... + kₙāₙ = Ō implies that k₁ = k₂ = ... = kₙ = 0.

Notes:

• Two collinear vectors are always linearly dependent.
• Two non-collinear non-zero vectors are always linearly independent
• Three coplanar vectors are always linearly dependent.
• Three non-coplanar non-zero vectors are always linearly independent.
• More than 3 vectors are always linearly dependent.

Orthogonal System of Vectors

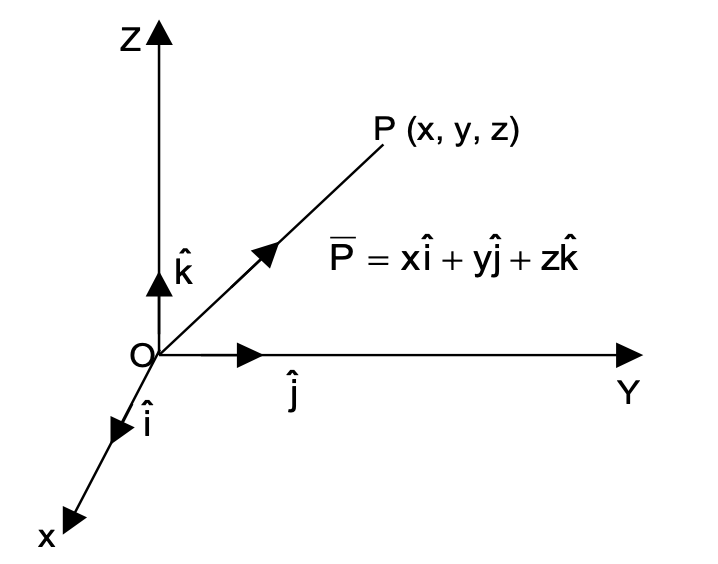
In the orthogonal system of vectors we choose three mutually perpendicular unit vectors denoted by ⁠î, ⁠ĵ, and directed along the positive directions of X, Y and Z axes respectively.

Corresponding to any point P(x, y, z) we can associate a vector w.r.t. a fixed orthogonal system then the position vector of P = x⁠î + y⁠ĵ + z⁠

|OP| = √x² + y² + z².

x, y, z are called the components of the vector.

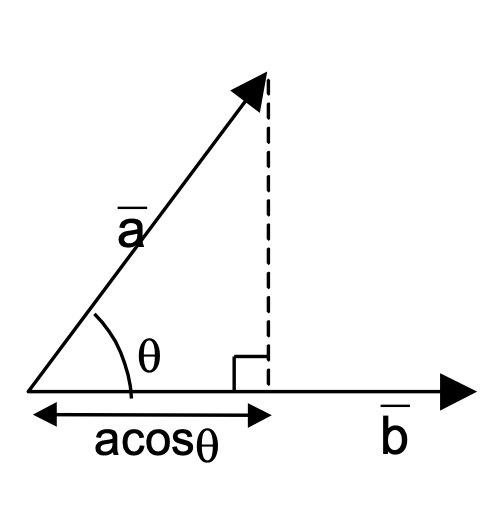
Scalar (or Dot) Product of Two Vectors

The scalar product of ̄a and ̄b, written as ̄a · ̄b, is defined to be the |̄a||̄b| cosθ, where θ is the angle between the vectors ̄a and ̄b i.e., ̄a · ̄b = abcosθ.

Properties:

• a • a = |a|² = a² ⇒ i • i = j • j = k • k = 1
• (|a|) • (mb) = |m(a • b)|
• a • b = 0 ↔ a, b are perpendicular to each other ⇒ i • j = j • k = k • i = 0
• (a ± b)² = a² + b² ± 2a • b
• If a = a₁i + a₂j + a₃k and b = b₁i + b₂j + b₃k then a • b = a₁b₁ + a₂b₂ + a₃b₃
• If a, b are non-zero, the angle between them is given by cos θ = a • b / |a| |b|
  = a₁b₁ + a₂b₂ + a₃b₃ / ( √(a₁² + a₂² + a₃²) √(b₁² + b₂² + b₃²) )

Vector OR Cross Product of Two Vectors

The vector product of two vectors a and b, denoted by a × b, is defined as the vector |a||b| sin θ n^̂, where θ is the angle between the vectors a and b and n^̂ is a unit vector perpendicular to both a and b (i.e., perpendicular to the plane of a and b).

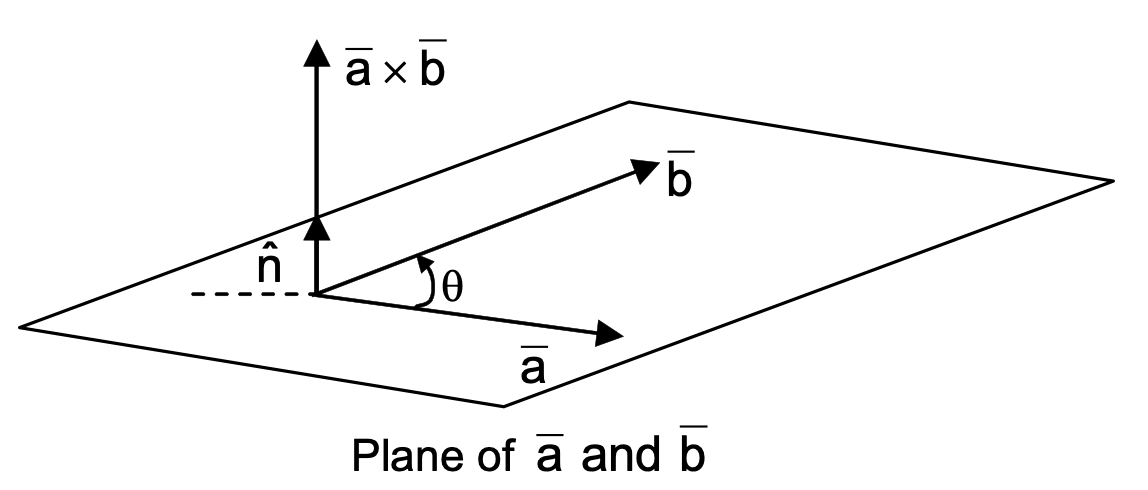
Properties:

• 𝒂 × 𝒂 = 𝟎 ⇒ î × î = ĵ × ĵ = k̂ × k̂ = 𝟎
• 𝒂 × 𝒃 = −(𝒃 × 𝒂) (non-commutative)
• (l𝒂) × (m𝒃) = lm(𝒂 × 𝒃)
• 𝒂 × 𝒃 = 𝟎 ⇔ 𝒂 and 𝒃 are collinear (if none of 𝒂, or 𝒃 is a zero vector)
• î × ĵ = k̂, ĵ × k̂ = î, k̂ × î = ĵ
  ĵ × î = −k̂, k̂ × ĵ = −î, î × k̂ = −ĵ
• If a = a₁î + a₂ĵ + a₃k̂ and b = b₁î + b₂ĵ + b₃k̂,
  then 𝒂 × 𝒃 =

  î	ĵ	k̂
  a1	a2	a3
  b1	b2	b3

• = (a₂b₃ − a₃b₂)î + (a₃b₁ − a₁b₃)ĵ + (a₁b₂ − a₂b₁)k̂
• Any vector perpendicular to the plane of 𝒂 and 𝒃 is λ(𝒂 × 𝒃) where λ is a real number.
  Unit vector perpendicular to 𝒂 and 𝒃 is ± (𝒂 × 𝒃) / |𝒂 × 𝒃|.
• | a × b | denotes the area of the parallelogram OACB, whereas area of ΔOAB = ½ | a × b |.

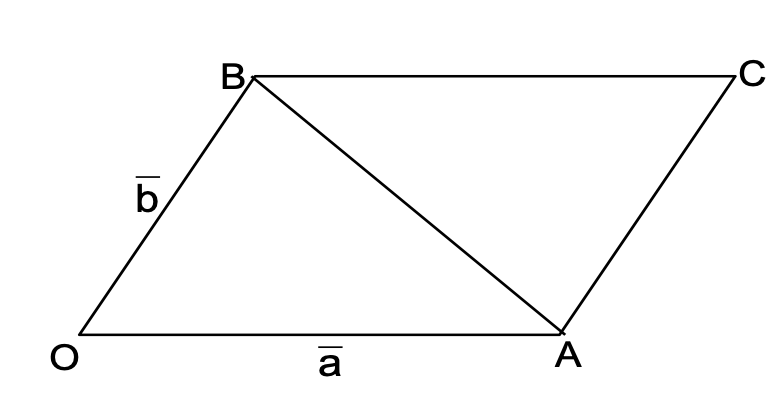
SCALAR TRIPLE PRODUCT
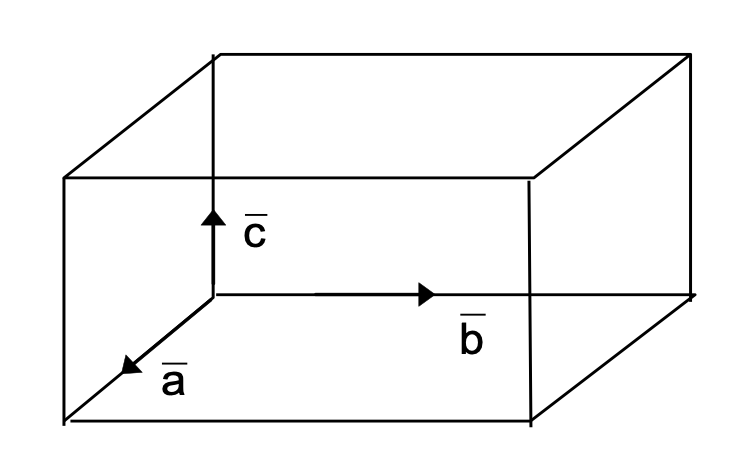
It is defined for three vectors a, b, c as the scalar (a × b) · c. The volume of the parallelepiped formed by taking a, b, c as the co-terminus edges.
V = magnitude of a × b · c = | a × b · c |.

Properties:

• a × b · c =

  | a₁ a₂ a₃ |
  | b₁ b₂ b₃ |
  | c₁ c₂ c₃ |
   

• a × b · c = a · b × c it is represented by [a b c]
• [a b c] = [b c a] = [c a b].
• [a b c] = -[b a c]
• [ka b c] = k[a b c]
• [a + bcd] = [a c d] + [b c d]

Vector Trile Product

It is defined for three vectors as the vector a × (b × c) = (a · c)b − (a · b)c.

COLLINEAR AND COPLANAR VECTORS

• Two vectors 𝑝̅ and 𝑞̅ are collinear if there exists k∈ℝ such that 𝑝̅ = k𝑞̅.

• Three points A(𝑎̅), B(𝑏̅), C(𝑐̅) are collinear if there exists k∈ℝ such that 𝐴𝐵̅ = k(𝐵𝐶̅), that is 𝑏̅−𝑎̅ = k(𝑐̅−𝑏̅).

• Three vectors 𝑝̅, 𝑞̅, 𝑟̅ are coplanar if there exists l, m∈ℝ such that 𝑟̅ = l𝑝̅ + m𝑞̅, i.e., one can be expressed as a linear combination of the other two.

• If [𝑝̅ 𝑞̅ 𝑟̅] = 0, then 𝑝̅, 𝑞̅, and 𝑟̅ are coplanar (necessary and sufficient condition).

• Four points A(𝑎̅), B(𝑏̅), C(𝑐̅) and D(𝑑̅) lie in the same plane if there exist l, m∈ℝ such that 𝐴𝐵̅ = l(𝐵𝐶̅) + m(𝐶𝐷̅).

• If [𝑏̅−𝑎̅ 𝑐̅−𝑏̅ 𝑑̅−𝑐̅] = 0, then A, B, C, D are coplanar.

Vector Equation of a Straight Line

(i) Line passing through a given point A (a) and parallel to a vector (b):
r = a + λb

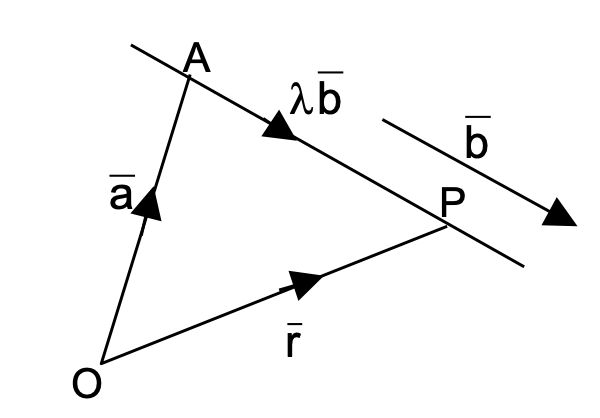
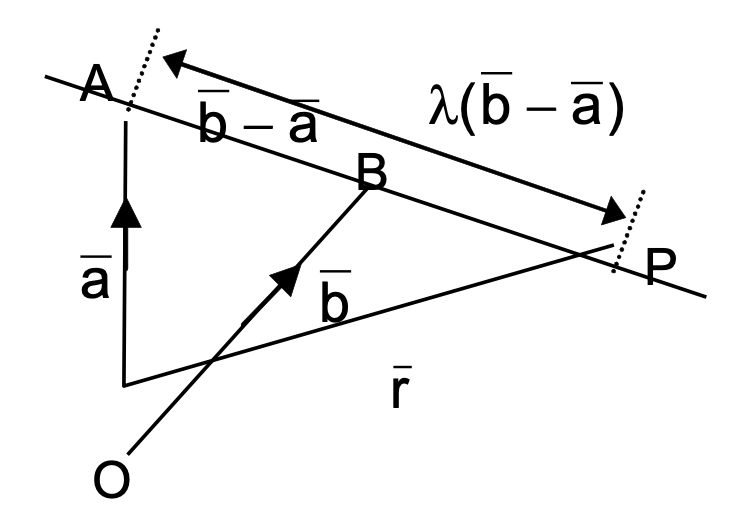
(ii) Line passing through two given points A (a) and B (b):
r = a + λ(b – a)

Angle Bisectors and Shortest Distance Between Two LinesAngle Bisectors

The internal bisector of angle between unit vectors â and b̂ is along the vector â + b̂.
The external bisector is along â – b̂.
Equation of internal and external bisectors of the lines r̄₁ = ā + λb̄₁ and r̄₂ = ā + μb̄₂ (intersecting at A(ā)) are given by

r̄ = ā + t ( b̄₁ / |b̄₁| ± b̄₂ / |b̄₂| ) .

Shortest Distance between Two Lines

Let r̄ = ā₁ + λb̄₁ and r̄ = ā₂ + μb̄₂ be two lines.

(i) They intersect if (b̄₁ × b̄₂) · (ā₂ – ā₁) = 0 .

(ii) They are parallel if b̄₁ and b̄₂ are collinear. Parallel lines are of the form r̄ = ā₁ + λb̄ and r̄ = ā₂ + λb̄ .

Perpendicular distance between them is constant and is equal to

b × (ā₂ – ā₁) / |b̄| .

Equation of a Plane in Vector Form
(i) A plane at a perpendicular distance d from the origin and normal to a given direction (n^̂) has the equation (r^̂ – dn^̂) · n^̂ = 0
or r̅ · n^̂ = d ( n^̂ is a unit vector).

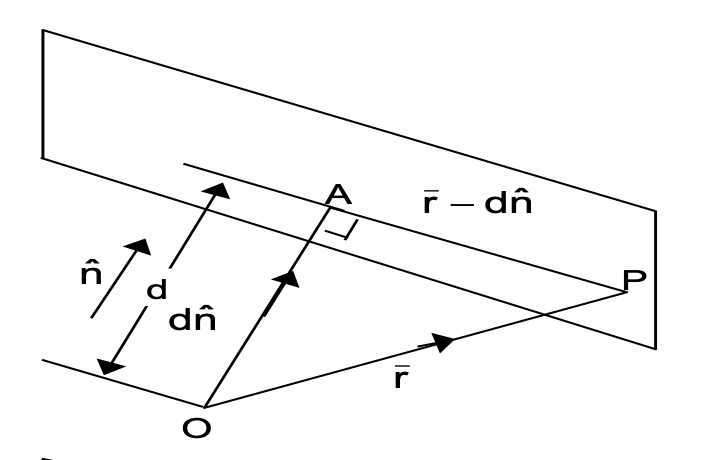
Plane Equation Extract(ii) A plane passing through the point A (a) and normal to n̂ has the equation (r – a) · n̂ = 0.

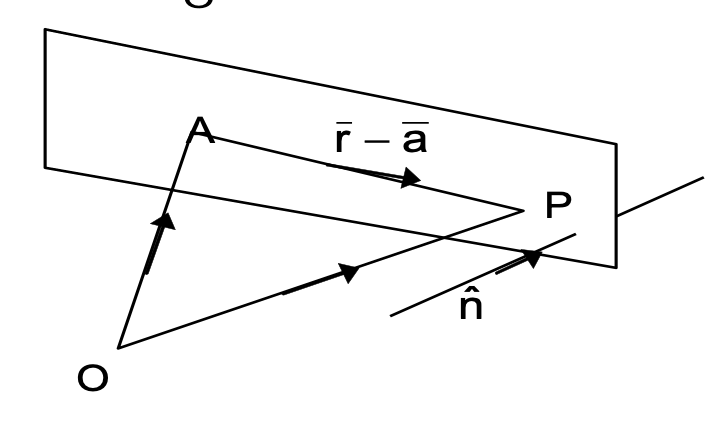
(iii) Parametric equation of the plane passing through A(̄a) and parallel to the plane of vectors (̄b) and (̄c) is given by
̄r = ̄a + λ̄b + μ̄c ⇒ ̄r · (̄b × ̄c) = [̄a ̄b ̄c].

(iv) Parametric equation of the plane passing through A(̄a), B(̄b), C(̄c) (A, B, C non-collinear) is given by
̄r = (1 - λ - μ)̄a + λ̄b + μ̄c ⇒ ̄r · [̄b × ̄c + ̄c × ̄a + ̄a × ̄b] = [̄a ̄b ̄c].

The perpendicular distance of the plane Ax + By + Cz = D from the origin is

|D|/√A² + B² + C² .

Angle between a Line and a Plane

The angle between a line and a plane is the complement of the angle between the line and the normal to the plane.

Angle Between Two Planes

It is equal to the angle between their normal unit vectors n̂₁ and n̂₂. i.e. cosθ = n̂₁ · n̂₂.

SOME MISCELLANEOUS RESULTS

(i) Volume of the tetrahedron ABCD = (1/6)[AB AC AD].

(ii) Area of the quadrilateral with diagonals d₁ and d₂ = (1/2) |d₁ × d₂|.

SOME MISCELLANEOUS RESULTS

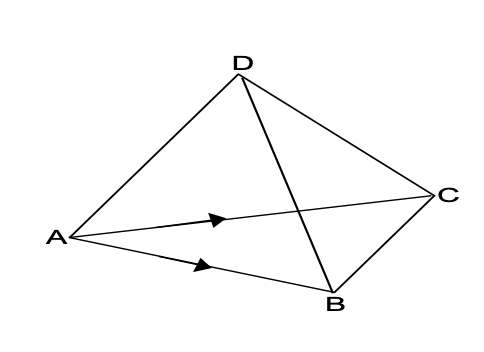
(i)  Volume of the tetrahedron ABCD = (1/6)[AB AC AD].

(ii)  Area of the quadrilateral with diagonals d₁ and d₂ = (1/2) |d₁ × d₂|.

Example: a and b are two non-zero vectors, then a and b make equal angles with c if

(A) a = (|b| / (|a| + |b|)) b + (|a| / (|a| + |b|)) c

(B) c = (|b| / (|a| + |b|)) a + (|a| / (|a| + |b|)) b

(C) c = (|b| / (|a| + |b|)) a + (|a| / (|a| + |b|)) b

(D) none of these

Solution: (C). It is evident that c is along the bisector of the angle between the vectors a and b.

⇒ c = λ ( a / |a| + b / |b| ) = λ ( (|b| a + |a| b) / (|a| |b|) )

If we take λ = (|a| |b|) / (|a| + |b|),

Then c = (|a| |b|) / (|a| + |b|) ( (|b| a + |a| b) / (|a| |b|) ) = (|b| / (|a| + |b|)) a + (|a| / (|a| + |b|)) b.

FORMULAE AND CONCEPTS AT A GLANCE

1. Three coplanar vectors are always linearly dependent.
2. a · b = |a||b| cosθ where θ is the angle between the vectors a and b
3. a · b = 0 ⇔ a, b are perpendicular to each other
4. a × b = |a||b| sinθ n̂, where θ is the angle between the vectors a, b and n̂ is a unit vector perpendicular to both a and b
5. a × a = 0
6. a × b = 0 ⇔ a and b are collinear (if none of a or b is a zero vector)
7. î × ĵ = k̂, ĵ × k̂ = î, k̂ × î = ĵ and ĵ × î = -k̂, k̂ × ĵ = -î, î × k̂ = -ĵ
8.  Any vector perpendicular to the plane of a and b is λ (a × b), where λ is a real number. Unit vector perpendicular to a and b is ± (a × b)/|a × b|.
9. |a × b| denotes the area of the parallelogram OACB, where OA̅ = a and OB̅ = b.
10. (a × b) · c = [a b c], which can also be written simply as a × b · c.
11. The volume of the parallelepiped formed by taking a, b, c as the coterminus edges, V = magnitude of a × b · c = |a × b · c|.
12. [a b c] = [b c a] = [c a b]
13. [ka b c] = k[a b c]

14. Equation of the line passing through a given point A (̄a) and parallel to a vector (̄b) is given by r̄ = ā + λb̄, where r̄ is the position vector of any general point P on the line and λ is a real number.

15. Equation of the line passing through two given points A (̄a) and B (̄a) is given by r̄ = ā + λ(b̄ – ā).

16. A plane at a perpendicular distance d from the origin and normal to a given direction (n̂) has the equation (r̄ – d n̂) · d n̂ = 0 or r̄ · n̂ = d (n̂ is a unit vector).

17. A plane passing through the point A (̄a) and normal to n̂ has the equation (r̄ – ā) · n̂ = 0.

18. Parametric equation of the plane passing through A (̄a) and parallel to the plane of vectors (̄b) and (̄c) is given by r̄ = ā + λb̄ + μc̄ ⇒ r̄ · (b̄ × c̄) = [ā b̄ c̄].

19. Volume of the tetrahedron ABCD = 1/6 [AB AC AD].