Applications of Trigonometry

Complete Class 10 Applications of Trigonometry Notes with Examples

Class 10 Applications of Trigonometry Notes focus on the practical use of trigonometric concepts to solve real-world problems. These notes cover heights and distances, angles of elevation and depression, and solving triangles using trigonometric ratios. Each topic is explained with examples, step-by-step solutions, and practice exercises. Understanding these applications is essential for problem-solving in mathematics, physics, and engineering. The notes also provide tips for identifying which trigonometric method to apply and shortcuts for fast calculations. By using these notes, Class 10 students can confidently approach board exams and competitive tests. They also help improve analytical thinking and logical reasoning by applying theoretical concepts to practical problems. After reading the note, solving NCERT questions with the help of the NCERT Solutions for class 10 Maths will help in building the foundation.

Class 10 Applications of Trigonometry Notes, Solved example & Questions

Trigonometry is a branch of mathematics that studies the relationships between angles and sides of triangles. Its applications extend far beyond theory, finding use in engineering, astronomy, navigation, architecture, and everyday problem-solving. From calculating the height of a building to determining the speed of an airplane, trigonometric principles provide accurate results when direct measurement is difficult or impossible

Line of Sight, Angle of Elevation, and Angle of Depression

The line of sight refers to the straight line drawn from an observer’s eye to an object.

• Angle of Elevation: When the object is above the horizontal level of the observer’s eye, the angle between the line of sight and the horizontal is called the angle of elevation. For example, observing the top of a tower or the sun in the sky involves this angle
• Angle of Depression: When the object is below the observer’s eye level, the line of sight forms the angle of depression with the horizontal. For example, a person looking down from a balcony to the street is measuring this angle

These concepts form the basis of many height and distance problems in trigonometry, as illustrated in the solved examples from the document (e.g., finding the height of a tower from given elevation angles).

Practical Applications

1. Height and Distance Measurement:

   Trigonometric ratios such as sine, cosine, and tangent are used to calculate heights of towers, trees, and buildings without direct measurement.

2. Navigation and Astronomy:

   Angles of elevation help determine the position of celestial objects, while depression angles are essential for navigation and surveying.

3. Engineering and Design:

   Architects and engineers use trigonometry to design inclined structures, bridges, and tools with precise measurements.

For example, as shown in the PDF exercises, one can calculate the distance of a ship from a lighthouse using angles of depression, or determine how far a balloon has traveled based on changes in its elevation angle

Key Trigonometric Formulas in Applications

The following table consolidates essential formulas used in height-and-distance problems:

Formula Name	Mathematical Representation	Explanation
Tangent of an angle	tan θ = opposite/adjaent	Relates vertical height to horizontal distance.
Angle of elevation problem	h = d. tanθ	Height (h) of an object at distance (d).
Angle of depression problem	h = d. tanθ	Distance or depth below line of sight.
Distance using two elevations	h = d1d2 (tanα. tanβ)/d2 tanα - d1 tanβ)	Calculates object height using two observation points.
Speed from elevation change	v=Δt/Δs	Finds speed of an object (e.g., airplane) using trigonometric distances.

 

LINE OF SIGHT

When an observer looks from a point O at an object P then the line OP is called the line of sight.

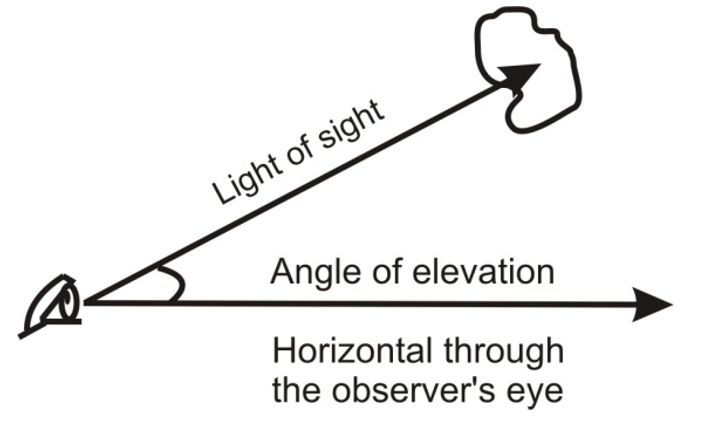
ANGLE OF ELEVATION

In order to see an object which is at a higher level compared to the ground level have are to look up. The line joining the object and the eye of the observer is known as the line of sight and the angle which this line of sight makes with the horizontal drawn through the eye of the observer is known as the angle of elevation. Therefore, the angle of elevation of an object helps in finding out its height.

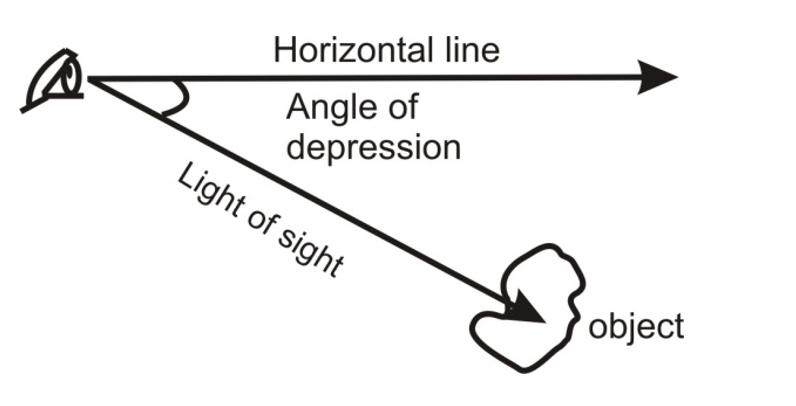
ANGLE OF DEPRESSION

When the object is at a lower level than the observer’s eyes, he has to look downwards to have a view of the object. In that case, the angle which the line of sight makes with the horizontal through the observer’s eye is known as the angle of depression (Figure).

Ex.: Find the angle of elevation of the Sun's altitude when the height of shadow of a vertical pole is equal to its height.

Sol.:

Let the height of the pole AB = x m.

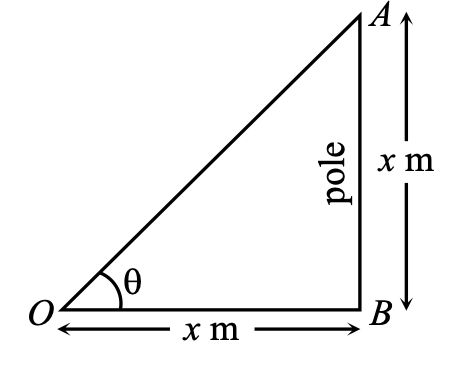
Then length of shadow OB of the pole AB = x m.
[∴ height of shadow = height of pole]

Let the angle of elevation be θ, i.e. ∠AOB = θ.

&tan; θ = AB / OB = x / x ⇒ &tan; θ = 1 ⇒ θ = 45°

Hence, the angle of elevation of the Sun's altitude is 45°.

Ex.: In figure, what are the angle of depression of the top and bottom of h m tall building from the top of multistoried building?

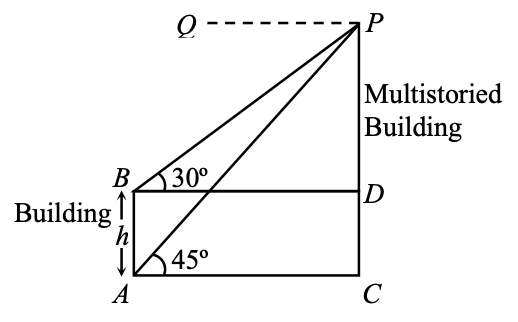
From P draw a line PQ ∥ BD or AC, then the angles of depression of the top and bottom of a tall building h m from the top P of the multistoried building are 30° and 45°, respectively.

Ex.: In figure, what are the angles of depression of the top and bottom of a pole from the top of a tower h m high?

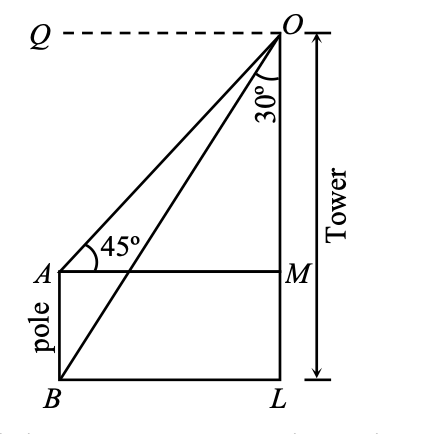
Sol. From O draw a line OQ parallel to AM or BL, then the angles of depression of the top and bottom of a pole from the top O of a tower h m are 45º and 60º respectively.

Ex.: A vertical tower stands on a horizontal plane and is surmounted by vertical flag staff of height 5 meters. At a point on the plane, the angle of elevation of the bottom and the top of the flag staff are respectively 30^o and 60^o. Find the height of tower.

Sol.

Let AB be the tower of height h meter and BC be the height of flag staff surmounted on the tower. Let the point of the place be D at a distance 'x' meter from the foot of the tower.

[Diagram: Vertical tower AB with flag staff BC on top, point D on ground, angles marked as 30° and 60°]

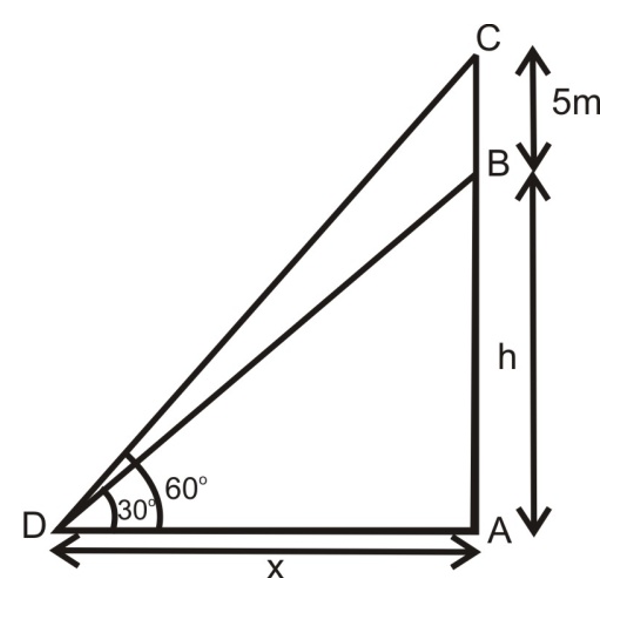
In △ABD:

tan 30° = AB/BD
⇒ 1/√3 = h/x
⇒ h = x/√3 .....(i)

In △ABD:

tan 60° = AC/BD
⇒ √3 = (h+5)/x
⇒ h + 5 = √3x .....(ii)

From (i) and (ii):

x/√3 + 5 = √3x
⇒ x + 5√3 = 3x
⇒ 5√3 = 3x - x
⇒ 5√3 = 2x
⇒ x = 5√3/2

Substituting in equation (i):
h = (5√3/2) / √3
h = 5/2
h = 2.5 m

So, the height of tower = 2.5 m.

Ex.: The angles of depressions of the top and bottom of 8m tall building from the top of a multistoried building are 30^o and 45^o respectively. Find the height of multistoried building and the distance between the two buildings.

Sol.

Let AB be the multistoried building of height h and let the distance between the two buildings be x meters.

[Diagram: Two buildings - multistoried building AB and 8m building DE, with angles of depression 30° and 45° marked]

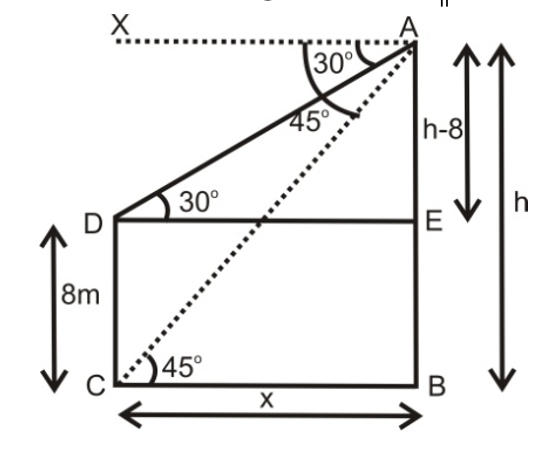
Note:

∠ABC = ∠ADE = 30° [Alternate angles, AX || DE]

∠ACB = ∠ACB = 45° [Alternate angles, AX || BC]

In △ADE:

tan 30° = AE/DE
⇒ 1/√3 = (h-8)/x
⇒ h - 8 = x/√3 .....(i)
(CB = DE = x)

In △ACB:

tan 45° = AB/BC
⇒ 1 = h/x
⇒ h = x .....(ii)

From (i) and (ii):

h = x/√3 + 8
⇒ x = x/√3 + 8
⇒ x - x/√3 = 8
⇒ x(1 - 1/√3) = 8
⇒ x[(√3 - 1)/√3] = 8
⇒ x = 8√3/(√3 - 1)

Rationalizing:
x = 8√3(√3 + 1)/[(√3 - 1)(√3 + 1)]
x = 8√3(√3 + 1)/(3 - 1)
x = 8√3(√3 + 1)/2
x = 4√3(√3 + 1)
x = 4(3 + √3) metres

From (ii): x = h

So, x = 4(3 + √3) metres.

Hence, height of multistoried building = 4(3 + √3) metres.
Distance between two buildings = 4(3 + √3) metres.

Ex.: The angle of elevation of an aeroplane from a point on the ground is 45^o. After a flight of 15 sec, the elevation changes to 30^o. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.

Sol.

Let the point on the ground is E which is y metres from point B and let after 15 sec flight it covers x metres distance.

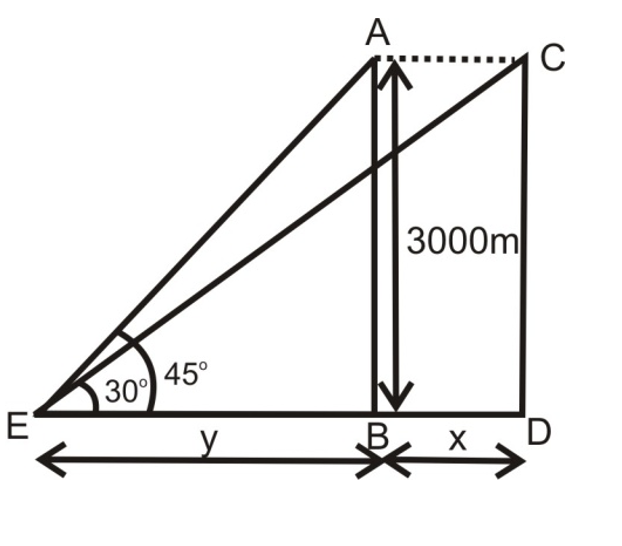
[Diagram: Aeroplane at two positions - initial position at angle 45° and final position at angle 30° from ground point E, flying at height 3000m]

In △AEB:

tan 45° = AB/BE
⇒ 1 = 3000/y
⇒ y = 3000 .....(i)

In △CED:

tan 30° = CD/DE
⇒ 1/√3 = 3000/(x+y)
⇒ x + y = 3000√3 .....(ii)

From equation (i) and (ii):

x + 3000 = 3000√3
⇒ x = 3000√3 - 3000
⇒ x = 3000(√3 - 1)
⇒ x = 3000(1.732 - 1)
⇒ x = 3000 × 0.732
⇒ x = 2196 metres

Speed of Aeroplane:

Speed = Distance/Time
Speed = 2196 metres / 15 seconds
Speed = 146.4 m/s

Converting to Km/hr:
Speed = 146.4 × (18/5)
Speed = 146.4 × 3.6
Speed = 527.04 Km/hr

Hence, the speed of aeroplane is 527.04 Km/hr.

Trigonometry is not just a theoretical concept but a powerful mathematical tool for solving real-world problems. By applying angles of elevation and depression, one can determine heights, distances, and even motion parameters without direct measurement. For students, mastering these applications is key to excelling in competitive exams and applying mathematics in practical life scenarios.