Coordinate Geometry

Detailed Class 10 Coordinate Geometry Notes for Quick Revision

Class 10 Coordinate Geometry Notes cover the fundamental concepts of points, distance formula, midpoint formula, section formula, and slope of a line. These notes are designed to make learning coordinate geometry easier and more practical with stepwise explanations and solved examples. Students can practice plotting points, calculating distances between points, finding midpoints, and solving related problems. Understanding coordinate geometry is essential for algebra, trigonometry, and real-life applications in physics and engineering. These notes also provide shortcuts, tips, and tricks to solve problems faster during exams. With structured practice exercises, students can strengthen their conceptual clarity, improve graphing skills, and confidently attempt questions in Class 10 board exams. The notes are suitable for regular learning as well as last-minute revision, ensuring students are well-prepared to tackle coordinate geometry questions effectively. Solving the NCERT questions with the help of the NCERT Solutions for class 10 Maths will help in building the foundation

Class 10 Coordinate Geometry Notes, Solved example & Questions

RECTANGULAR CO-ORDINATES

Take two perpendicular lines X'OX and Y'OY intersecting at the point O. X'OX and Y'OY are called the co-ordinate axes. X'OX is called the X-axis, Y'OY is called the Y-axis and O is called the origin. Lines X'OX and Y'OY are sometimes also called rectangular axes.

Figure 1: Rectangular Coordinate Axes

CO-ORDINATES OF A POINT

Let P be any point as shown in the figure. Draw PL and PM perpendiculars on Y-axis and X-axis, respectively. The length LP (or OM) is called the x-coordinate or the abscissa of point P and MP is called the y-coordinate or the ordinate of point P. A point whose abscissa is x and ordinate is y is named as the point (x, y) or P(x, y).

Figure 2: Coordinates of a Point

The two lines X'OX and Y'OY divide the plane into four parts called quadrants. XOY, YOX', X'OY' and Y'OX are, respectively, called the first, second, third and fourth quadrants. The following table shows the signs of the coordinates of points situated in different quadrants:

Quadrant	X-coordinate	Y-coordinate	Point
First quadrant	+	+	(+, +)
Second quadrant	−	+	(−, +)
Third quadrant	−	−	(−, −)
Fourth quadrant	+	−	(+, −)

REMARKS

(i) Abscissa is the perpendicular distance of a point from y-axis (i.e., positive to the right of y-axis and negative to the left of y-axis)

(ii)Ordinate is positive above x-axis and negative below x-axis.

(iii)Abscissa of any point on y-axis is zero.

(iv)Ordinate of any point on x-axis is zero.

(v) Co-ordinates of the origin are (0, 0).

Do Check - Real Numbers

DISTANCE FORMULAE

The distance between two points P(x₁, y₁) and Q(x₂, y₂) is given by the formula:

PQ = √[(x₂ − x₁)² + (y₂ − y₁)²]

Proof of Distance Formula

Draw PR and QS perpendicular to the x-axis. A perpendicular from the point P on QS is drawn to meet it at the point T.

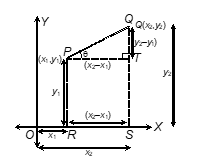
Figure 3: Distance Formula Proof

Then OR = x₁, OS = x₂, So, RS = x₂ − x₁ = PT.

Also SQ = y₂, ST = PR = y₁. So, QT = y₂ − y₁.

Now applying the Pythagoras theorem in ΔPTQ,

we get PQ² = PT² + QT²

= (x₂ − x₁)² + (y₂ − y₁)².

Therefore, PQ = √[(x₂ − x₁)² + (y₂ − y₁)²]

Since distance is always non-negative, we take only the positive square root. So the distance between the points P(x₁, y₁) and Q(x₂, y₂) is

PQ = √[(x₂ − x₁)² + (y₂ − y₁)²]

which is called the distance formula.

Special Case: In particular, the distance of a point P(x, y) from the origin O(0, 0) is given by:

OP = √(x² + y²)

SOME USEFUL POINTS

1. In questions relating to geometrical figures, take the given vertices in the given order and proceed as indicated.

• (i) For an isosceles triangle - We have to prove that at least two sides are equal.
• (ii) For an equilateral triangle - We have to prove that three sides are equal.
• (iii) For a right-angled triangle - We have to prove that the sum of the squares of two sides is equal to the square of the third side.
• (iv) For a square - We have to prove that the four sides are equal, two diagonals are equal.
• (v) For a rhombus - We have to prove that four sides are equal (and there is no need to establish that two diagonals are unequal as the square is also a rhombus).
• (vi) For a rectangle - We have to prove that the opposite sides are equal and two diagonals are equal.
• (vii) For a Parallelogram - We have to prove that the opposite sides are equal (and there is no need to establish that two diagonals are unequal as the rectangle is also a parallelogram).

2. For three points to be collinear - We have to prove that the sum of the distances between two pairs of points is equal to the third pair of points.

SOLVED EXAMPLES ON DISTANCE FORMULA

Example 1: Find the distance between the points (8, −2) and (3, −6).

Solution: Let the points (8, −2) and (3, −6) be denoted by P and Q, respectively.

Then, by distance formula, we obtain the distance PQ as

PQ = √[(3 − 8)² + (−6 − (−2))²]

= √[(−5)² + (−4)²]

= √[25 + 16]

= √41 Unit

Example 2: Find the distance between the points P(−6, 7) and Q(−1, −5).

Solution: Here, x₁ = −6, y₁ = 7 and x₂ = −1, y₂ = −5

∴ PQ = √[(−1 − (−6))² + (−5 − 7)²]

⇒ PQ = √[(5)² + (−12)²]

⇒ PQ = √[25 + 144] = √169 = 13

Example 3: Show that the points (1, −1), (5, 2) and (9, 5) are collinear.

Solution: Let A(1, −1), B(5, 2) and C(9, 5) be the given points. Then we have

AB = √[(5 − 1)² + (2 − (−1))²] = √[16 + 9] = √25 = 5

BC = √[(9 − 5)² + (5 − 2)²] = √[16 + 9] = √25 = 5

and AC = √[(9 − 1)² + (5 − (−1))²] = √[64 + 36] = √100 = 10

Clearly, AC = AB + BC.

Hence, A, B, C are collinear points.

Example 4: Prove that the points (1, −1), (5, 2) and (1, 2) are the vertices of an isosceles triangle.

Solution: Let the points (1, −1), (5, 2) and (1, 2) be denoted by P, Q and R, respectively. Now

PQ = √[(5 − 1)² + (2 − (−1))²] = √[16 + 9] = √25 = 5

QR = √[(1 − 5)² + (2 − 2)²] = √[16 + 0] = √16 = 4

PR = √[(1 − 1)² + (2 − (−1))²] = √[0 + 9] = √9 = 3

From the above, we see that PQ ≠ QR ≠ PR.

Note: The example appears to have calculation inconsistencies in the original document. For an isosceles triangle, at least two sides must be equal.

Do Check - polynomials

Example 5: Using distance formula, show that the points (−3, 2), (1, −2) and (9, −10) are collinear.

Solution: Let the given points (−3, 2), (1, −2) and (9, −10) be denoted by A, B and C, respectively. Points A, B and C will be collinear, if the sum of the lengths of two line-segments is equal to the third.

Now, AB = √[(1 − (−3))² + (−2 − 2)²] = √[16 + 16] = √32 = 4√2

BC = √[(9 − 1)² + (−10 − (−2))²] = √[64 + 64] = √128 = 8√2

AC = √[(9 − (−3))² + (−10 − 2)²] = √[144 + 144] = √288 = 12√2

Since, AB + BC = 4√2 + 8√2 = 12√2 = AC, the points A, B and C are collinear.

Example 6: Find a point on the X-axis which is equidistant from the points (5, 4) and (−2, 3).

Solution: Since the required point (say P) is on the X-axis, its ordinate will be zero. Let the abscissa of the point be x.

Therefore, coordinates of the point P are (x, 0).

Let A and B denote the points (5, 4) and (−2, 3), respectively.

Since we are given that AP = BP, we have

AP² = BP².

i.e., (x − 5)² + (0 − 4)² = (x + 2)² + (0 − 3)²

or x² + 25 − 10x + 16 = x² + 4 + 4x + 9

or −14x = −28

or x = 2.

Thus the required point is (2, 0).

Example 7: If the distance of P(x, y) from A(5, 1) and B(−1, 5) are equal, prove that 3x = 2y.

Solution: P(x, y), A(5, 1) and B(−1, 5) are the given points.

AP = BP. (Given)

∴ AP² = BP²

or AP² − BP² = 0

or {(x − 5)² + (y − 1)²} − {(x + 1)² + (y − 5)²} = 0

or x² + 25 − 10x + y² + 1 − 2y − x² − 1 − 2x − y² − 25 + 10y = 0

or −12x + 8y = 0

or 3x = 2y.

Do Check - Linear Equations

SECTION FORMULAE

FORMULA FOR INTERNAL DIVISION

The coordinates of the point which divides the line segment joining the points (x₁, y₁) and (x₂, y₂) internally in the ratio m : n are given by:

x = (mx₂ + nx₁)/(m + n), y = (my₂ + ny₁)/(m + n)

Proof of Internal Division Formula

Let O be the origin and let OX and OY be the X-axis and Y-axis respectively. Let A(x₁, y₁) and B(x₂, y₂) be the given points. Let (x, y) be the coordinates of the point P which divides AB internally in the ratio m : n. Draw AL ⊥ OX, BM ⊥ OX, PN ⊥ OX. Also draw AH and PK perpendicular from A and P on PN and BM respectively. Then

OL = x₁, ON = x, OM = x₂, AL = y₁, PN = y and BM = y₂.

∴ AH = LN = ON − OL = x − x₁, PH = PN − HN

= PN − AL = y − y₁, PK = NM = OM − ON = x₂ − x

and BK = BM − MK = BM − PN = y₂ − y.

Figure 4: Internal Division of a Line Segment

Clearly, ΔAHP and ΔPKB are similar.

∴ AH/PK = PH/BK = AP/PB = m/n

⇒ (x − x₁)/(x₂ − x) = m/n and (y − y₁)/(y₂ − y) = m/n

Now, (x − x₁)/(x₂ − x) = m/n

⇒ mx₂ − mx = nx − nx₁ ⇒ mx + nx = mx₂ + nx₁

⇒ x = (mx₂ + nx₁)/(m + n)

And (y − y₁)/(y₂ − y) = m/n

⇒ my₂ − my = ny − ny₁ ⇒ my + ny = my₂ + ny₁

⇒ y = (my₂ + ny₁)/(m + n)

Thus the coordinates of P are ((mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n))

FORMULA FOR EXTERNAL DIVISION

The coordinates of the point which divides the line segment joining the points (x₁, y₁) and (x₂, y₂) externally in the ratio m : n are given by:

x = (mx₂ − nx₁)/(m − n), y = (my₂ − ny₁)/(m − n)

MIDPOINT FORMULAE

The coordinates of the midpoint M of a line segment AB with end points A(x₁, y₁) and B(x₂, y₂) are:

M = ((x₁ + x₂)/2, (y₁ + y₂)/2)

Proof of Midpoint Formula

Let M be the midpoint of the line segment joining the points A(x₁, y₁) and B(x₂, y₂).

Then M divides AB in the ratio 1 : 1.

So by the section formula, the coordinates of M are

((1 × x₂ + 1 × x₁)/(1 + 1), (1 × y₂ + 1 × y₁)/(1 + 1)), i.e., ((x₁ + x₂)/2, (y₁ + y₂)/2).

Hence the coordinates of the midpoint of AB are ((x₁ + x₂)/2, (y₁ + y₂)/2).

Note: The line joining the points (x₁, y₁) and (x₂, y₂) is divided by the y-axis in the ratio −x₁ : x₂ and by x-axis in the ratio −y₁ : y₂

Steps to Find the Ratio in Which a Line Divides the Line Joining Two Points

1. Let the ratio λ : 1.
2. Use the formula of internal division.
3. Evaluate the value of λ i.e., the ratio.
4. If λ is +ve then it is internal division and if λ is −ve then it is external division.

SOLVED EXAMPLES ON SECTION FORMULA

Example 1: Find the coordinates of the point which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 : 2 (i) internally (ii) externally.

Solution: Let P(x, y) be the required point.

(i) For internal division, we have

x = (3 × (−4) + 2 × 6)/(3 + 2) = (−12 + 12)/5 = 0/5 = 0

and y = (3 × 5 + 2 × 3)/(3 + 2) = (15 + 6)/5 = 21/5

⇒ x = 0 and y = 21/5.

So the coordinates of P are (0, 21/5).

(ii) For external division, we have

x = (3 × (−4) − 2 × 6)/(3 − 2) = (−12 − 12)/1 = −24

and y = (3 × 5 − 2 × 3)/(3 − 2) = (15 − 6)/1 = 9

⇒ x = −24 and y = 9.

So the coordinates of P are (−24, 9).

Do Check - Quadratic Equations

Example 2: In which ratio does the point (−1, −1) divide the line segment joining the points (4, 4) and (7, 7)?

Solution: Suppose the point C(−1, −1) divides the line joining the points A(4, 4) and B(7, 7) in the ratio k : 1. Then, the coordinates of C are ((7k + 4)/(k + 1), (7k + 4)/(k + 1)).

But we are given that the coordinates of the point C are (−1, −1).

∴ (7k + 4)/(k + 1) = −1

⇒ 7k + 4 = −k − 1

⇒ 8k = −5

⇒ k = −5/8

Thus C divides AB externally in the ratio 5 : 8.

Example 3: In what ratio does the X-axis divide the line segment joining the points (2, −3) and (5, 6)?

Solution: Let the required ratio be k : 1. Then the coordinates of the point of division are ((5k + 2)/(k + 1), (6k − 3)/(k + 1)). But it is a point on x-axis on which y-coordinate of every point is zero.

∴ (6k − 3)/(k + 1) = 0

⇒ 6k − 3 = 0

⇒ k = 3/6 = 1/2.

Thus, the required ratio is 1/2 : 1 or 1 : 2.

CENTROID OF A TRIANGLE

The point of intersection of the medians of a triangle is called the centroid of a triangle and it divides the median internally in the ratio 2 : 1.

Medians are the lines coming from one vertex and bisecting the opposite side. The coordinates of the centroid of a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) is given by:

G = ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)

Proof of Centroid Formula

Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of a ΔABC.

Let D be the midpoint of BC.

Then the coordinates of D by midpoint formula are ((x₂ + x₃)/2, (y₂ + y₃)/2).

Let G(x, y) be the centroid of ΔABC. Then G divides AD in the ratio 2 : 1.

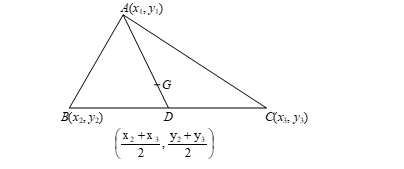
Figure 5: Centroid of a Triangle

∴ Using section formula:

x = [2 × ((x₂ + x₃)/2) + 1 × x₁]/(2 + 1)

= (x₂ + x₃ + x₁)/3 = (x₁ + x₂ + x₃)/3

y = [2 × ((y₂ + y₃)/2) + 1 × y₁]/(2 + 1)

= (y₂ + y₃ + y₁)/3 = (y₁ + y₂ + y₃)/3

Hence the coordinates of G are ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3).

Note: Centroid of the triangle obtained by joining the middle points of the triangle is same as the centroid of the original triangle.

SOLVED EXAMPLES ON CENTROID

Example 1: Find the centroid of ΔABC whose vertices are A(−3, 0), B(5, −2) and C(−8, 5). And hence also find the centroid of a triangle having the midpoints as vertices.

Solution: Here, x₁ = −3, y₁ = 0; x₂ = 5, y₂ = −2 and x₃ = −8, y₃ = 5

Let G(x, y) be the centroid of ΔABC. Then

x = (x₁ + x₂ + x₃)/3 = (−3 + 5 + (−8))/3 = −6/3 = −2

y = (y₁ + y₂ + y₃)/3 = (0 + (−2) + 5)/3 = 3/3 = 1

Hence, the centroid of ΔABC is G(−2, 1).

Again, let G' be the centroid of the triangle formed by joining the midpoints (by the help of the note in the previous page.)

The centroid will be the same: G'(−2, 1). Hence the centroid is (−2, 1).

AREA OF A TRIANGLE

The area of a ΔABC with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) is given by:

Area = (1/2) |x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|

Proof of Area Formula

Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of the given ΔABC.

Draw AP, BM and CN perpendiculars to the x-axis.

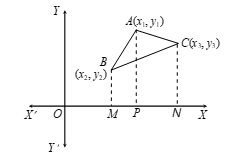
Figure 6: Area of a Triangle

Then AP = y₁, BM = y₂, CN = y₃, PM = x₂ − x₁, PN = x₃ − x₁

and MN = x₃ − x₂.

∴ Area of ΔABC

= ar (trap. BMPA) + ar (trap. APNC) − ar (trap. BMNC)

= (1/2)(BM + AP) × PM + (1/2)(AP + CN) × PN − (1/2)(BM + CN) × MN

= (1/2)(y₂ + y₁)(x₂ − x₁) + (1/2)(y₁ + y₃)(x₃ − x₁) − (1/2)(y₂ + y₃)(x₃ − x₂)

= (1/2)[x₁y₂ − x₁y₁ + x₂y₂ − x₂y₁ + x₁y₃ − x₁y₁ + x₃y₃ − x₃y₁ − x₃y₂ + x₂y₂ − x₃y₃ + x₂y₃]

= (1/2)[x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)]

Since the area is never negative, we have

Area = (1/2) |x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|

CONDITION FOR COLLINEARITY OF THREE POINTS

Let the given points be A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃).

Then A, B and C are collinear

⇒ area of ΔABC = 0

⇒ (1/2)[x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)] = 0

⇒ x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂) = 0

Do Check - Arithmetic Progressions

AREA OF QUADRILATERAL

Let the vertices of quadrilateral ABCD are A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) and D(x₄, y₄)

So, area of the quadrilateral ABCD = area of ΔABC + area of ΔACD

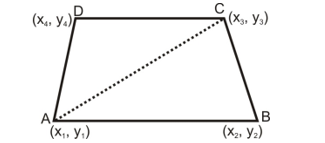
Figure 7: Area of a Quadrilateral

SOLVED EXAMPLE ON AREA OF QUADRILATERAL

Example 1: Find the area of quadrilateral whose vertices, taken in order, are A(−3, 2), B(5, 4), C(7, −6) and D(−5, −4).

Solution: Area of the quadrilateral ABCD = area of ΔABC + area of ΔACD

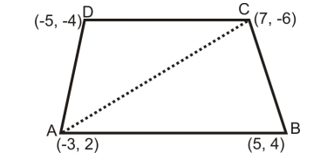
So, area of ΔABC = (1/2)|x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|

= (1/2)|(−3)(4 − (−6)) + 5(−6 − 2) + 7(2 − 4)|

= (1/2)|(−3)(10) + 5(−8) + 7(−2)|

= (1/2)|−30 − 40 − 14|

= (1/2)|−84| = 42 sq. units

Area of ΔACD = (1/2)|x₁(y₃ − y₄) + x₃(y₄ − y₁) + x₄(y₁ − y₃)|

= (1/2)|(−3)(−6 − (−4)) + 7(−4 − 2) + (−5)(2 − (−6))|

= (1/2)|(−3)(−2) + 7(−6) + (−5)(8)|

= (1/2)|6 − 42 − 40|

= (1/2)|−76| = 38 sq. units

So, area of the quadrilateral ABCD = 42 + 38 = 80 sq. units.

COORDINATE GEOMETRY - QUICK REFERENCE

• The coordinates of a point on x-axis are of the form (x, 0) and a point on y-axis are of the form (0, y).

Distance Formula

The distance between two points A(x₁, y₁) and B(x₂, y₂) is given by:

AB = √[(x₂ − x₁)² + (y₂ − y₁)²]

The distance of a point P(x, y) from the origin O(0, 0) is given by:

OP = √(x² + y²)

Section Formula

The co-ordinates of the point which divides the join of points A(x₁, y₁) and B(x₂, y₂) internally in the ratio m : n are:

((mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n))

Mid Point Formula

The coordinates of the mid-point of line segment joining the points A(x₁, y₁) and B(x₂, y₂) are:

((x₁ + x₂)/2, (y₁ + y₂)/2)

Centroid Formula

The coordinates of centroid of the triangle formed by the points A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are:

((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)

Area of Triangle

The area of a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) is:

Area = (1/2) |x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|

Collinear Points

Three points A, B, C are collinear if AB + BC = AC i.e., sum of distances between two pairs of points is equal to distance between third pair.

Three points A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are collinear if area of the triangle formed by these points is zero.

Properties of Geometric Shapes

• In a parallelogram, diagonals bisect each other.
• In a square all four sides are equal and both diagonals are equal.
• In a rectangle opposite sides and both diagonals are equal.

Coordinate Geometry - Theory & Practice Problems with Answers

Q. No.	Question
1.	Find a point on the X-axis which is equidistant from the points (5, 4) and (-2, 3).
2.	The vertices of a triangle are (-2, 0), (2, 3) and (1, -3). Is the triangle equilateral, isosceles or scalene?
3.	The length of a line segment is 10. If one end is at (2, -3) and the abscissa of the second end is 10, show that its ordinate is either 3 or -9.
4.	Show that the points (-2, 5), (3, -4) and (7, 10) are the vertices of a right triangle.
5.	Do the points A(3, 2), B(-2, -3) and C(2, 3) form a triangle? If so, name the type of the triangle formed.
6.	Find the coordinates of the circumcentre of a triangle whose vertices are A(4, 6), B(0, 4) and C(6, 2). Also, find its circumradius.
Answers:	1. (2, 0) | 2. ABC is a scalene triangle | 5. Right angled triangle | 6. Coordinates: P(3, 3), Circumradius = √10 units

Question 1: Find a point on the X-axis which is equidistant from the points (5, 4) and (-2, 3).

Sol. Since the required point (say P) is on the X-axis, its ordinate will be zero. Let the abscissa of the point be x.

Therefore, coordinates of the point P are (x, 0).

Let A and B denote the points (5, 4) and (-2, 3), respectively.

Since we are given that AP = BP, we have

AP² = BP²

i.e., (x - 5)² + (0 - 4)² = (x + 2)² + (0 - 3)²

or x² + 25 - 10x + 16 = x² + 4 + 4x + 9

or -14x = -28

or x = 2.

Thus the required point is (2, 0).

Question 2: The vertices of a triangle are (-2, 0), (2, 3) and (1, -3). Is the triangle equilateral, isosceles or scalene?

Sol. Let the points (-2, 0), (2, 3) and (1, -3) be denoted by A, B and C respectively. Then,

AB = √[(2 - (-2))² + (3 - 0)²] = √[16 + 9] = √25 = 5

BC = √[(1 - 2)² + (-3 - 3)²] = √[1 + 36] = √37

and AC = √[(1 - (-2))² + (-3 - 0)²] = √[9 + 9] = √18 = 3√2

Clearly, AB ≠ BC ≠ AC.

Therefore, ABC is a scalene triangle.

Question 3: The length of a line segment is 10. If one end is at (2, -3) and the abscissa of the second end is 10, show that its ordinate is either 3 or -9.

Sol. Let (2, -3) be the point A. Let the ordinate of the second end B be y. Then its coordinates will be (10, y).

Thus, AB = √[(10 - 2)² + (y - (-3))²] = 10

or √[64 + (y + 3)²] = 10

Squaring both sides:

or 64 + y² + 9 + 6y = 100

or y² + 6y + 73 - 100 = 0

or y² + 6y - 27 = 0

or (y + 9)(y - 3) = 0

Therefore, y = -9 or y = 3.

Question 4: Show that the points (-2, 5), (3, -4) and (7, 10) are the vertices of a right triangle.

Sol. Let the three points be A(-2, 5), B(3, -4), and C(7, 10).

Then AB² = (3 + 2)² + (-4 - 5)² = 25 + 81 = 106

BC² = (7 - 3)² + (10 + 4)² = 16 + 196 = 212

AC² = (7 + 2)² + (10 - 5)² = 81 + 25 = 106

We observe that BC² = AB² + AC²

212 = 106 + 106

Therefore, the triangle is right-angled at A.

Question 5: Do the points A(3, 2), B(−2, −3) and C(2, 3) form a triangle? If so, name the type of the triangle formed.

Sol. We have,

AB = √[(−2 − 3)² + (−3 − 2)²] = √[25 + 25] = √50 = 5√2

BC = √[(2 − (−2))² + (3 − (−3))²] = √[16 + 36] = √52 = 2√13

and, AC = √[(2 − 3)² + (3 − 2)²] = √[1 + 1] = √2

As AB + BC > AC, AC + BC > AB and AB + AC > BC. Therefore, points A, B and C form a triangle.

AB² = 50 and BC² = 52, AC² = 2.

∴ AB² + AC² = 50 + 2 = 52 = BC².

Therefore, ∆ABC is a right triangle, right angled at A.

Question 6: Find the coordinates of the circumcentre of a triangle whose vertices are A(4, 6), B(0, 4) and C(6, 2). Also, find its circumradius.

Sol. Let A(4, 6), B(0, 4) and C(6, 2) be the vertices of the given ∆ABC.

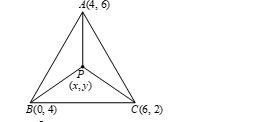
Figure: Circumcentre of Triangle ABC

Let P(x, y) be the circumcentre of ∆ABC.

Then PA = PB = PC

⇒ PA² = PB² = PC²

⇒ PA² = PB² and PB² = PC².

Now PA² = PB²

⇒ (x − 4)² + (y − 6)² = (x − 0)² + (y − 4)²

⇒ x² + 16 − 8x + y² + 36 − 12y = x² + y² + 16 − 8y

⇒ 8x + 4y = 36

⇒ 2x + y = 9 ..... (i)

Again PB² = PC²

⇒ (x − 0)² + (y − 4)² = (x − 6)² + (y − 2)²

⇒ x² + y² + 16 − 8y = x² + 36 − 12x + y² + 4 − 4y

⇒ 12x − 4y = 24 ⇒ 3x − y = 6. ..... (ii)

On solving (i) and (ii), we get x = 3 and y = 3.

∴ Coordinates of the circumcentre of ∆ABC are P(3, 3)

Circumradius = PA = √[(3 − 4)² + (3 − 6)²] = √[1 + 9] = √10 units.

Circumradius = √10 units.

Q. No.	Question
7.	Determine the ratio in which the line 2x + y − 4 = 0 divides the line joining the points (3, −1) and (8, 9).
8.	Find the coordinates of the point which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 : 2 internally.
9.	Find the ratio in which the y-axis divides the line segment joining the points (5, −6) and (−1, −4). Also find the point of intersection.
10.	In what ratio does the x-axis divide the line segment joining the points (2, −3) and (5, 6)? Also find the coordinates of the point of intersection.
11.	If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.
12.	Determine the ratio in which the line 3x + y − 9 = 0 divides the segment joining the points (1, 3) and (2, 7).
Answers:	7. 8 : 13 (externally) | 8. (0, 21/5) | 9. 5 : 1, (0, −29/6) | 10. 1 : 2, (3, 0) | 11.p = 7 | 12. 3 : 4

Question 7: Determine the ratio in which the line 2x + y − 4 = 0 divides the line joining the points (3, −1) and (8, 9).

Sol. Let the line 'L' divides the line joining the points (3, −1) and (8, 9) in the ratio λ : 1 at a point 'C' then

C = ((8λ + 3)/(λ + 1), (9λ − 1)/(λ + 1))

As C satisfies the line 2x + y − 4 = 0

2 × (8λ + 3)/(λ + 1) + (9λ − 1)/(λ + 1) − 4 = 0

⇒ (16λ + 6 + 9λ − 1 − 4λ − 4)/(λ + 1) = 0

⇒ 21λ + 1 = 0

⇒ λ = −1/21 = −8/13 (negative sign indicates external division)

Hence ratio is 8 : 13 externally.

Alternative Method: If the line ax + by + c = 0 divides the line joining the point (x₁, y₁) and (x₂, y₂) then the ratio is given by −(ax₁ + by₁ + c)/(ax₂ + by₂ + c).

Hence the ratio will be −[2(3) + (−1) − 4]/[2(8) + 9 − 4] = −1/21 = −8/13

Hence ratio is 8 : 13 externally.

Question 8: Find the coordinates of the point which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 : 2 internally.

Sol. Let P(x, y) be the required point. Then,

x = (3 × (−4) + 2 × 6)/(3 + 2) = (−12 + 12)/5 = 0/5 = 0

and y = (3 × 5 + 2 × 3)/(3 + 2) = (15 + 6)/5 = 21/5

⇒ x = 0 and y = 21/5.

Figure: Section Formula Application

So the coordinates of P are (0, 21/5).

Question 9: Find the ratio in which the y-axis divides the line segment joining the points (5, −6) and (−1, −4). Also find the point of intersection.

Sol. Let the ratio be k : 1. Then by the section formula, the coordinates of the point which divides AB in the ratio k : 1 are

((−k + 5)/(k + 1), (−4k − 6)/(k + 1)).

This point lies on the y-axis, ∴ its coordinates are (0, y).

∴ (−k + 5)/(k + 1) = 0

⇒ −k + 5 = 0

⇒ k = 5.

Thus the ratio is 5 : 1.

Putting the value of k = 5, we get the point of intersection

y = (−4(5) − 6)/(5 + 1) = −26/6 = −13/3 = −29/6

Point of intersection is (0, −29/6).

Alternative:y axis divides in the ratio −x₁ : x₂ i.e., −5 : (−1) = 5 : 1.

Question 10: In what ratio does the x-axis divide the line segment joining the points (2, −3) and (5, 6)? Also find the coordinates of the point of intersection.

Sol. Let the required ratio be k : 1. Then, the coordinates of the point R which divides PQ in the ratio k : 1 are

((5k + 2)/(k + 1), (6k − 3)/(k + 1)).

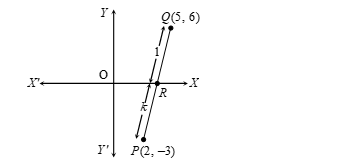
Figure: X-axis Division of Line Segment

This point lies on x-axis therefore its coordinates are (x, 0),

∴ (6k − 3)/(k + 1) = 0

⇒ 6k − 3 = 0

⇒ k = 3/6 = 1/2.

Thus, the required ratio is 1/2 : 1 or 1 : 2.

Putting k = 1/2 in the coordinates of R, we find that its coordinates are:

x = (5(1/2) + 2)/((1/2) + 1) = (5/2 + 2)/(3/2) = (9/2)/(3/2) = 3

Coordinates are (3, 0).

Question 11: If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.

Sol. In parallelogram ABCD

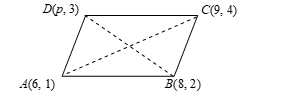
Figure: Parallelogram ABCD

coordinates of the mid-point of AC = coordinates of the mid-point of BD

⇒ ((6 + 9)/2, (1 + 4)/2) = ((8 + p)/2, (2 + 3)/2)

⇒ (15/2, 5/2) = ((8 + p)/2, 5/2)

⇒ 15/2 = (8 + p)/2

⇒ 30 = 16 + 2p

⇒ 14 = 2p

⇒ p = 7.

Question 12: Determine the ratio in which the line 3x + y − 9 = 0 divides the segment joining the points (1, 3) and (2, 7).

Sol. Suppose the line 3x + y − 9 = 0 divides the line segment joining A(1, 3) and B(2, 7) in the ratio k : 1 at point C. The coordinates of C is

((2k + 1)/(k + 1), (7k + 3)/(k + 1)).

But C lies on 3x + y − 9 = 0, therefore,

3 × (2k + 1)/(k + 1) + (7k + 3)/(k + 1) − 9 = 0

⇒ 6k + 3 + 7k + 3 − 9k − 9 = 0

⇒ 4k − 3 = 0

⇒ k = 3/4.

So the required ratio is 3 : 4 internally.

Area of Triangle Problems

Q. No.	Question
13.	Find the area of a triangle whose vertices are (1, −1), (−4, 6) and (−3, −5).
14.	Find the value of k if the points A(2, 3), B(4, k) and C(6, −3) are collinear.
15.	Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.
16.	Find the value of k for which the area formed by the triangle with vertices (0, 0), (3, 0) and (0, k) is 5 square units.
Answers:	13. 24 square units | 14. 0 | 16.k = ±10/3

Detailed Solutions

Question 13: Find the area of a triangle whose vertices are (1, −1), (−4, 6) and (−3, −5).

Sol. The area of the triangle formed by the vertices A(1, −1), B(−4, 6) and C(−3, −5) is given by

Area = (1/2)|x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|

= (1/2)|1(6 − (−5)) + (−4)(−5 − (−1)) + (−3)(−1 − 6)|

= (1/2)|1(11) + (−4)(−4) + (−3)(−7)|

= (1/2)|11 + 16 + 21|

= (1/2)|48| = 24

So the area of the triangle is 24 square units.

Question 14: Find the value of k if the points A(2, 3), B(4, k) and C(6, −3) are collinear.

Sol. Since the given points are collinear, the area of the triangle will be 0,

⇒ (1/2)|x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)| = 0

⇒ 2(k − (−3)) + 4(−3 − 3) + 6(3 − k) = 0

⇒ 2(k + 3) + 4(−6) + 6(3 − k) = 0

⇒ 2k + 6 − 24 + 18 − 6k = 0

⇒ −4k = 0

Therefore, k = 0.

Question 15: Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.

Sol. Let ∆ be the area of the triangle formed by the points (a, b + c), (b, c + a) and (c, a + b)

⇒ ∆ = (1/2)|a(c + a − a − b) + b(a + b − b − c) + c(b + c − c − a)|

⇒ ∆ = (1/2)|a(c − b) + b(a − c) + c(b − a)|

⇒ ∆ = (1/2)|ac − ab + ab − bc + bc − ac|

⇒ ∆ = (1/2)|0| = 0

Since area is zero therefore, the given points are collinear.

Question 16: Find the value of k for which the area formed by the triangle with vertices (0, 0), (3, 0) and (0, k) is 5 square units.

Sol. The vertices of the given ∆ABC are A(0, 0), B(3, 0) and C(0, k).

∴ x₁ = 0, y₁ = 0; x₂ = 3, y₂ = 0 and x₃ = 0, y₃ = k.

Area of ∆ABC

= (1/2)|x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|

= (1/2)|0(0 − k) + 3(k − 0) + 0(0 − 0)|

= (1/2)|3k|

= (3/2)|k| sq units.

But area of ∆ABC = 5 sq units. [given]

∴ (3/2)|k| = 5

⇒ |k| = 10/3 or k = ±10/3

Hence k = 10/3 or k = −10/3.

Comprehensive Solved Examples

Illustration 1: Find the value of x, if the distance between the points (x, −1) and (3, 2) is 5.

Sol. Let P(x, −1) and Q(3, 2) be the given points. Then PQ = 5

⇒ √[(x − 3)² + (−1 − 2)²] = 5 or √[(x − 3)² + 9] = 5

Squaring both sides:

⇒ (x − 3)² + 9 = 25

⇒ (x − 3)² = 16

⇒ x − 3 = ±4 ⇒ x = 3 ± 4

⇒ (x − 7)(x + 1) = 0 ⇒ x = 7 or, x = −1.

Therefore, x = 7 or x = −1.

Illustration 2: Find a point on x-axis which is equidistant from A(2, −5) and B(−2, 9).

Sol. Let P(x, 0) be the point equidistant from A(2, −5) and B(−2, 9). Then PA = PB

⇒ PA² = PB²

⇒ (x − 2)² + (0 − (−5))² = (x − (−2))² + (0 − 9)²

⇒ x² + 4 − 4x + 25 = x² + 4 + 4x + 81

⇒ −4x + 29 = 4x + 85

⇒ −8x = 56 ⇒ x = −7.

Hence the required point is (−7, 0).

Illustration 3: Prove that the points (−3, 0), (1, −3) and (4, 1) are the vertices of an isosceles right-angled triangle.

Sol. Let A(−3, 0), B(1, −3) and C(4, 1) be the given points. Then,

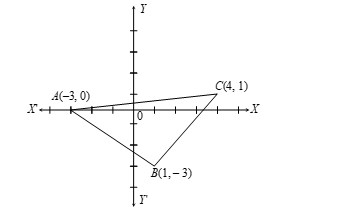
Figure: Isosceles Right-Angled Triangle

AB = √[(1 − (−3))² + (−3 − 0)²]

= √[16 + 9] = √25 = 5 units

BC = √[(4 − 1)² + (1 − (−3))²]

= √[9 + 16] = √25 = 5 units

and, AC = √[(4 − (−3))² + (1 − 0)²]

= √[49 + 1] = √50 = 5√2 units

⇒ AB = BC.

Therefore, ∆ABC is isosceles.

Also AC² = 50 = 25 + 25 = AB² + BC².

∆ABC is right-angled at B. Thus ∆ABC is a right-angled isosceles triangle.