Complete Class 10 Construction Notes with Easy Steps
Class 10 Construction Notes focus on geometric constructions with accuracy, including constructing triangles, tangents to circles, bisecting angles, and dividing lines into given ratios. These notes provide step-by-step explanations and diagrams to help students visualize constructions easily. Understanding construction is crucial for geometry, practical problem-solving, and developing logical thinking. The notes include tips, shortcuts, and practice exercises for board exam preparation and revision. By following these notes, students can quickly learn to construct geometric figures accurately, solve construction problems efficiently, and gain confidence in exams. They are ideal for Class 10 students who want clear, structured guidance to master all construction-related questions, ensuring strong performance in mathematics. After reading the note, solving NCERT questions with the help of the NCERT Solutions for class 10 Maths will help in building the foundation.
Class 10 Construction Notes, Solved example & Questions
Optics: Definitions, Concepts, and Expert Constructions
Optics, a foundational branch of physics, delves into the behavior, propagation, and interaction of light. Essential topics in geometric optics include construction theory, methods for dividing line segments and constructing similar triangles, and the mathematical basis for understanding reflection, refraction, and tangency in circles. Precision in geometric construction, clarity in definitions, and knowledge of key formulas help build expertise and trust in the learning process.
Construction Theory in Optics
Construction theory in optics involves geometrically dividing line segments or constructing figures using specific ratios. For example, dividing a line segment AB into a ratio m:nm:n requires drawing an auxiliary ray, marking off proportional points, and using parallel lines, which ensures accurate and repeatable division required in lens manufacturing or scientific modeling. Techniques for constructing similar triangles or quadrilaterals based on side ratios are essential in designing optics setups and verifying theoretical models.
Tangents to Circles: Applications and Instructions
Tangent lines play a crucial role in optics, especially for understanding contact points on lenses or mirrors. A tangent is always perpendicular to the radius at the contact point. From an external point, two equal tangents can be drawn to a circle, aiding in laser setup and ray diagramming. The content also covers drawing tangents without knowledge of the circle’s center, a useful technique in geometrical problems and advanced applications where the center isn’t marked.
Authoritative Explanations: Real-World Examples
The document expands on construction techniques for triangles and quadrilaterals similar to given figures, applying scale factors to all sides. This skill is vital for students constructing optical models, calculating image sizes, or mapping out reflection paths in experiments. The exercises included reinforce conceptual mastery through structured problem-solving, enabling learners to practice and verify actual measurements, such as tangent lengths and angle divisions.
Key Formulas in Optics
| Formula Name | Mathematical Representation | Explanation |
|---|---|---|
| Law of Reflection | θi = θr | Angle of incidence equals angle of reflection. |
| Snell’s Law (Refraction) | n1 sin θ1 = n2 sinθ2 | Governs light bending between two media. |
| Circle Tangent Length (External pt) | L = | Length LL from external point distance dd to radius rr. |
| Basic Proportionality Theorem | AP/PB = m/n | Divide segment AB internally in m:nm:n ratio. |
| Pythagorean Theorem (Tangency Proof) | a2 + b2 = c2 | Used to verify tangent lengths, especially in right triangles. |
Expertise and Trust: Structured Learning for Optics
This coverage synthesizes theory with step-by-step construction methods, ensuring a strong basis in geometric optics. Definitions and processes are grounded in sound mathematical logic and hands-on experience. The well-explained formulas and construction techniques give confidence to educators, students, and technical professionals, supporting deep conceptual mastery.
Applications and Learning Enhancement
Students can apply these skills in geometry labs, competitive exams, and real-world optics setups. Educators benefit from the scientific clarity and verified solutions, providing trust and experience in teaching advanced topics in optics. Exercises and models presented foster active learning and practical understanding
Introduction to Geometric Construction
Geometric construction is a fundamental skill in mathematics that involves creating precise geometric figures using only basic tools such as a compass, straightedge, and pencil. This ancient art, dating back to the Greek mathematicians, forms the foundation of many mathematical concepts and practical applications in engineering, architecture, and design.
Key Concepts Covered:
- Division of line segments in a given ratio using two different methods
- Construction of similar triangles with specified scale factors
- Construction of tangents to circles from external and internal points
- Application of the Basic Proportionality Theorem
Division of a Line Segment
Definition
The division of a line segment internally in a given ratio m:n means finding a point P on the line segment AB such that the ratio of AP to PB equals m:n, where both m and n are positive integers.
When we divide a line segment AB internally in the ratio m:n, we are essentially finding a point P on AB such that AP:PB = m:n. This construction has numerous practical applications in architecture, engineering design, and scale modeling.
Method 1: Standard Method for Line Segment Division
Steps of Construction:
- Step 1: Draw a line segment AB of given length using a ruler. Mark the endpoints clearly as points A and B.
- Step 2: Draw a ray AX making an acute angle with AB. The angle should be less than 90 degrees to ensure proper construction and visibility of subsequent points.
- Step 3: Along ray AX, mark off (m + n) points A₁, A₂, A₃, ..., Am+n such that AA₁ = A₁A₂ = A₂A₃ = ... = Am+n-1Am+n. These points must be equally spaced along the ray.
- Step 4: Join point B to the last point Am+n on ray AX. This creates a line segment BAm+n.
- Step 5: Through the point Am (the m-th point), draw a line parallel to Am+nB by making an angle equal to ∠AAm+nB at Am. Suppose this parallel line meets AB at point P.
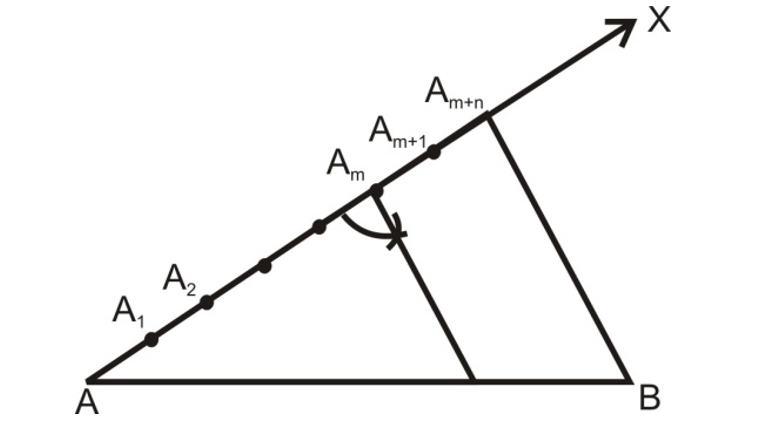
Figure 1: Division of a line segment in a given ratio using the standard method
Result: The point P so obtained is the required point which divides AB internally in the ratio m:n.
Example: Dividing a Line Segment in the Ratio 3:2
Problem Statement:
Given a line segment AB, divide it in the ratio 3:2.
Detailed Solution:
- Draw any ray AX, making an acute angle with AB. This angle should be convenient for construction, typically between 30° and 60°.
- Locate 5 (= m + n = 3 + 2) points A₁, A₂, A₃, A₄, and A₅ on AX such that:
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅
Use a compass to ensure equal spacing between consecutive points. - Join point B to A₅, creating line segment BA₅.
- Through point A₃ (since m = 3), draw a line parallel to A₅B by making an angle equal to ∠AA₅B. This parallel line intersects AB at point C.
Conclusion: Point C divides AB such that AC:CB = 3:2
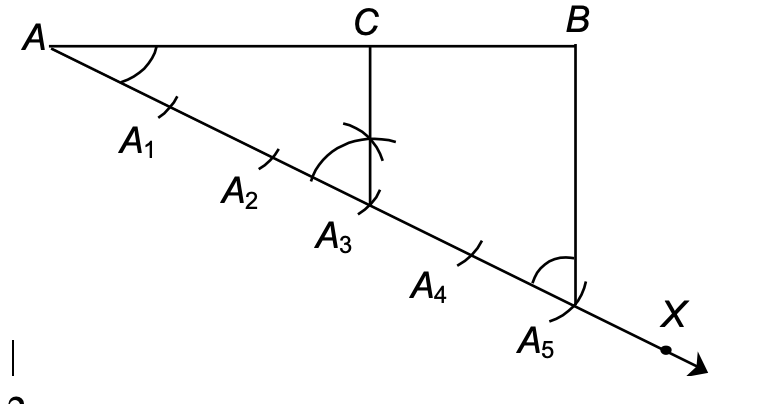
Mathematical Justification
The construction works based on the Basic Proportionality Theorem (also known as Thales' Theorem). Since the line through A₃ is parallel to A₅B, we can apply this theorem to triangles formed by these lines.
By Basic Proportionality Theorem: AA₃/A₃A₅ = AC/CB
Since by construction, AA₃ contains 3 equal segments and A₃A₅ contains 2 equal segments, we have:
AC/CB = 3/2
This proves that point C divides AB in the ratio 3:2.
Method 2: Alternative Method for Line Segment Division
This alternative method provides a different approach to dividing a line segment internally in a given ratio m:n. This method is particularly useful when working with certain geometric constraints or when a symmetrical construction is preferred.
Steps of Construction:
- Step 1: Draw a line segment AB of given length using a ruler.
- Step 2: Draw any ray AX making an acute angle ∠BAX with AB.
- Step 3: Draw a ray BY on the opposite side of AX, parallel to AX, making an angle ∠ABY equal to ∠BAX. This creates a symmetrical configuration.
- Step 4: Mark off m points A₁, A₂, ..., Am on ray AX and n points B₁, B₂, ..., Bn on ray BY such that:
AA₁ = A₁A₂ = ... = Am-1Am = BB₁ = B₁B₂ = ... = Bn-1Bn
- Step 5: Join AmBn. Suppose it intersects AB at point P.
Result: Point P is the required point dividing AB in the ratio m:n.
Alternative method for division of a line segment internally in a given ratio
Use the following steps to divide a given line segment AB internally in a given ration m : n, where m and natural members.
STEPS OF CONSTRUCTION:
(i) Draw a line segment AB of given length.
(ii) Draw any ray AX making an acute angle ∠BAX with AB.
(iii) Draw a ray BY, on opposite side of AX, parallel to AX making an angle ∠ABY equal to ∠BAX.
(iv) Mark off a points A₁, A₂,...,Aₘ, on AX and n points B₁, B₂,...,Bₙ on BY such that AA₁ = A₁A₂ = ...... = Aₘ₋₁Aₘ = B₁B₂ = ....Bₙ₋₁Bₙ.
(v) Join AₘBₙ. Suppose it intersect AB at P.
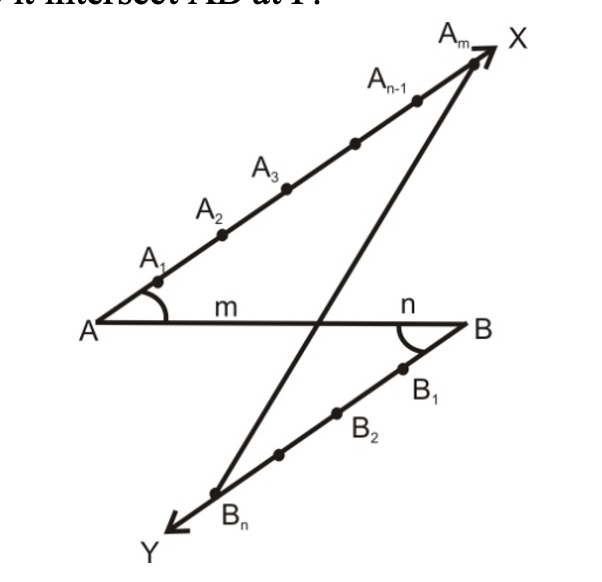
-
A horizontal line segment AB with points A and B marked
-
Ray AX extending upward from A with points A₁, A₂, A₃, Aₘ₋₁, Aₘ, and X marked along it
-
Ray BY extending downward from B with points B₁, B₂, Bₙ, and Y marked along it
-
Point P where line AₘBₙ intersects AB
-
Labels showing "m" and "n" segments on line AB]
The point P is the required point dividing AB in the ratio m : n.
This geometric construction method allows division of a line segment in any given ratio m:n by creating equal divisions on two parallel rays and connecting specific points to find the division point on the original segment.
Example. Decide a line segment of length 6 cm internally in the ratio 3:4.
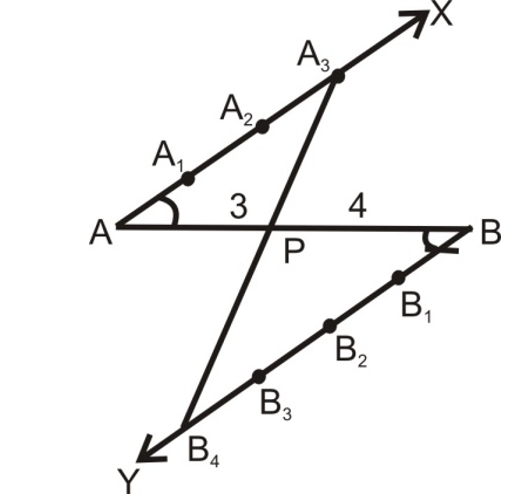
Sol. Follow the following steps:
STEPS OF CONSTRUCTION:
(i) Draw a line segment AB of length 6 cm.
(ii) Draw any ray AX making an acute angle ∠BAX with AB.
(iii) Draw a ray BY parallel to AX by making ∠ABY equal to ∠BAX.
(iv) Mark of three points A₁, A₂, A₃ on AX and 4 points B₁, B₂, B₃, B₄ on BY such that AA₁ = A₁A₂ = A₂A₃ = BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
(v) Join A₃B₄. Suppose it intersects AB at a point P. Then, P is the point dividing AB internally in the ratio 3:4.
Construction of A triangle similar to a given triangle
Scale Factor:
The ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle is known as their scale factor.
Steps of Construction when m < n:
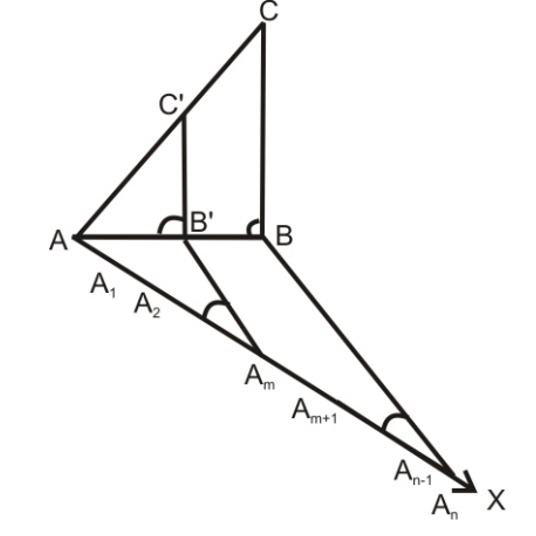
-
Construct the given triangle ABC by using the given data.
-
Take any one of the three sides of the given triangle as the base. Let AB be the base of the given triangle.
-
At one end, say A, of the base AB, construct an acute angle ∠BAX∠BAX below the base AB.
-
Along AX, mark n points A1,A2,A3,…,AnA1,A2,A3,…,An such that AA1=A1A2=…=An−1AnAA1=A1A2=…=An−1An.
-
Join AnAn to B.
-
Draw AmB′ parallel to AnB which meets AB at B′.
-
From B′ draw B′C′∥CB meeting AC at C′.
Triangle AB′C′ is the required triangle each of whose side is (m/n)th of the corresponding side of △ABC.
Ex.: Construction a △ABC in which AB = 5cm, BC = 6cm and AC = 7cm. Now, construct a triangle similar to △ABC such that each of its side is two-third of the corresponding side of △ABC.
Sol. Steps of Construction
(i) Draw a line segment AB = 5 cm.
(ii) With AA as centre and radius AC=7cm, draw an arc.
(iii) With BB as centre and BC = 6cm, draw another arc, intersecting the arc drawn in step (ii) at C.
(iv) Join AC and BC to obtain △ABC.
(v) Below ABAB, make an acute angle ∠BAX.
(vi) Along AX, mark off three points (greater of 2 and 3 in 2/3) A1,A2,A3 such that A1A2 = A2A3.
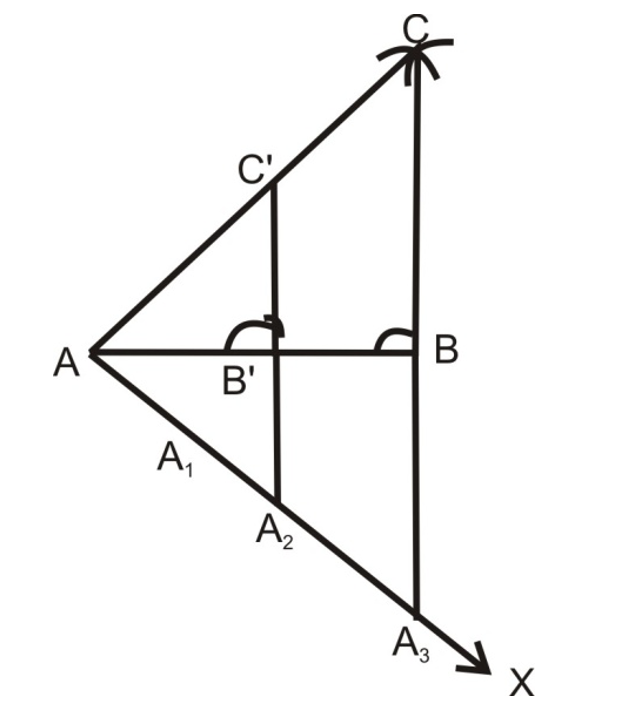
(vii) Join A₃B.
(viii) Draw A₂B' ∥ A₃B, meeting AB at B'.
(iv) From B', draw B'C' ∥ BC, meeting AC at C'.
AB'C' is the required triangle, each of the whose sides is two-third of the corresponding sides of △ABC.
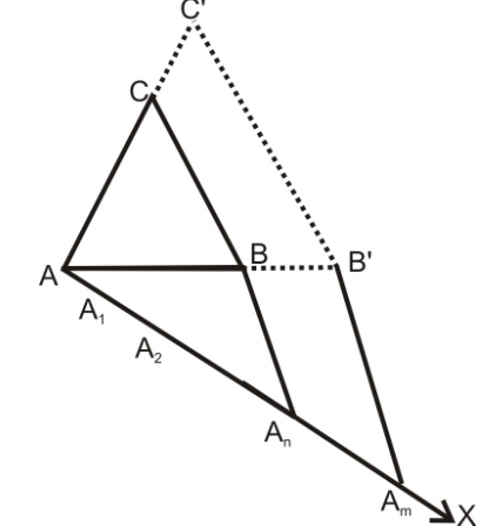
Steps of Construction when m > n:
(i) Construct the given triangle by using the given data.
(ii) Take any of the three sides of the given triangle and consider it as the base. Let AB be the base of the given triangle.
Here is the text conversion of the image with all mathematical symbols and expressions:
(iii) At one end, say A, of base AB construct an acute angle ∠BAX below base AB i.e. on the composite side of the vertex C.
(iv) Along AX, mark-off m (large of m and n) points A₁, A₂,.....,Aₘ on AX such that AA₁ = A₁A₂ = .... Aₘ₋₁Aₘ.
(v) Join Aₙ to B and draw a line through Aₘ parallel to Aₙ B, intersecting the extended line segment AB at B'.
(vi) Draw a line through B' parallel to BC intersecting the extended line segment AC at C'.
(vii) ΔABC' so obtained is the required triangle.
[The image shows a geometric construction with:
- Triangle ABC (original triangle with vertices A, B, C)
- Point X on a ray from A below the base AB
- Points A₁, A₂, Aₙ, Aₘ marked sequentially along AX
- Point B' on the extension of AB
- Point C' on the extension of AC
- Dotted lines showing the parallel constructions from Aₘ to B' and from B' to C'
- The final triangle AB'C' is the enlarged triangle]
Construction of Tangents from a point outside the circle
When centre is given:
⇒ When point of tangency is on the circle.
Given: A circle with centre O.
Required: To draw a tangent from point P on the circle.
Steps of construction:
- Take a point O on the plane of the paper and draw a circle of given radius.
- Take a point P on the circle.
- Join OP.
- Construct ∠OPX = 90°.
- Produce XP to Y to get XPY as the required tangent.
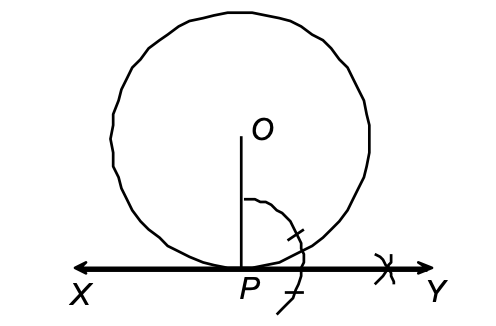
[DIAGRAM showing a circle with center O, point P on the circle, radius OP drawn vertically, and a horizontal tangent line XPY passing through P perpendicular to OP]
⇒ When point of tangency is outside the circle
Given: A circle with centre O.
Required: To draw a tangent from an external point, i.e. P.
Steps of construction:
- Join the centre O of the circle to the given external point, i.e. P.
- Draw ⊥ bisector of OP, intersecting OP at O′
- Taking O′ as centre and OO′ = PO′ as radius, draw a circle to intersect the given circle at T and T′
- Join PT and PT′ to get the required tangents as PT and PT′.
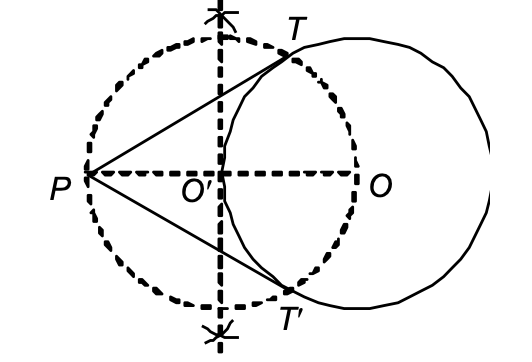
WHEN CENTRE IS NOT GIVEN:
⇒ When point of tangency is on the circles.
Given: A circle and a point P on it.
Required: To draw a tangent at P without using centre of the circle.
Steps of construction:
- Draw any chord PQ of the circle through P as in figure.
- Take any point R on the major arc PQ and join PR and QR.
- Construct ∠QPX equal to ∠PRQ.
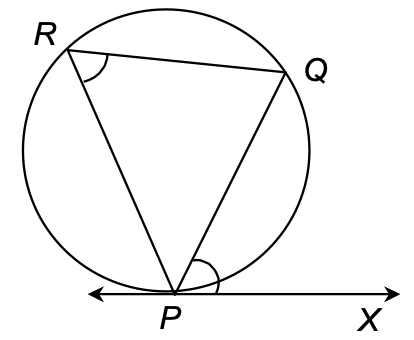
[THIS IS FIGURE: A circle with points P, Q, and R marked. R is on the major arc. Lines PR and QR are drawn forming a triangle. A line PX extends from P as a tangent to the circle.]
Then PX is the required tangent at P to the circle.
⇒ When point of tangency is outside the circle.
Given: A circle and a point P outside it.
Required: To draw a tangent from point P without using the centre.
Steps of construction:
- Let P be the external point from where the tangents are to be drawn to the given circle.
- Through P draw a secant PAB to intersect the circle at A and B.
- Produce AP to a point C such that AP = PC.
- Draw a semi-circle with BC as diameter.
- Draw PD ⊥ CB, intersecting the semi-circle at D.
- With P as centre and PD as radius draw arcs to intersect the given circle at T and T'.
- Joint PT and PT'. PT and PT' are the required tangents.
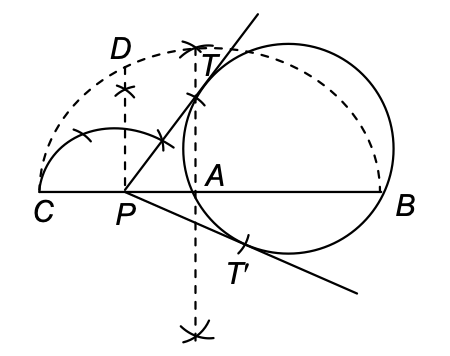
Ex.: Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
Given:
(i) A circle with centre O and radius 6 cm.
(ii) A point P at a distance of 10 cm from O.
Required:
To draw two tangents to the circle from point P and measure the lengths of the tangents.
Steps of construction:
- Bisect the line-segment OP. Let the point of bisection be M.
- Taking M as centre and OM as radius, draw a circle. Let is intersect the circle at the points Q and R.
- Join PQ and PR. These are the required tangents. On measuring, PQ = PR = 8 cm.
Diagram:
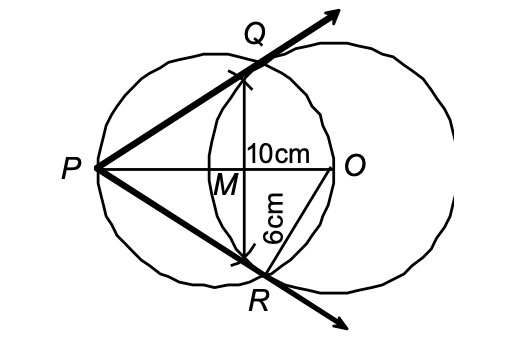
The diagram shows:
- A circle with centre O and radius 6 cm
- Point P at distance 10 cm from O
- Point M is the midpoint of OP
- A larger circle with centre M and radius OM
- Points Q and R where the larger circle intersects the original circle
- Tangent lines PQ and PR drawn from P to the circle
- The measurements show OP = 10 cm and the radius = 6 cm
- The tangent lengths PQ = PR = 8 cm
Ex.: Draw tangents from an external point P to a circle of radius 4 cm without using the centre.
Sol. Given: A circle of radius 4 cm.
Required: To draw two tangents from an external point P.
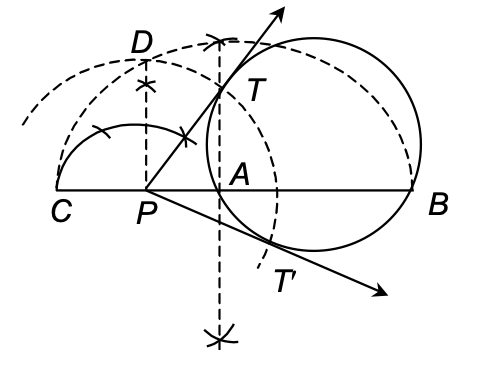
Steps of construction:
- Draw a circle of radius 4 cm.
- Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.
- Produce AP to C such that PA = CP.
- Draw a semi-circle with CB as diameter.
- Draw PD ⊥ CB, intersecting the semi-circle at D.
- With P as centre and PD as radius draw arcs to intersect the given circle at T and T′.
- Join PT and PT′. Then PT and PT′ are the required tangents.
In this comprehensive guide, we will explore the systematic methods for dividing line segments in given ratios and constructing triangles similar to given triangles. These construction techniques are essential for understanding proportionality, similarity, and the fundamental principles of Euclidean geometry.