Detailed Class 10 Areas Related to Circles Notes
Class 10 Areas Related to Circles Notes cover sectors, segments, and other circle-related areas with clear explanations, formulas, and solved examples. These notes focus on applying the right formula to calculate areas accurately and efficiently. Understanding areas related to circles is important for problem-solving, geometry, and practical applications in real-life situations. The notes provide stepwise solutions, shortcuts, and tips for fast calculation, making revision easier and exam preparation more effective. With practice exercises included, students can improve their accuracy, speed, and conceptual understanding. These notes are perfect for Class 10 students who want to strengthen their knowledge and confidently solve questions related to areas of circles in board exams and competitive tests. Studnets must solve the NCERT questions with the help of the NCERT Solutions for class 10 Maths, which will help in building the foundation.
Class 10 Areas Related to Circles Notes, Solved example & Questions
Circle
The set of points which are at a constant distance of units from a fixed point O is called a circle with centre O and radius = r units. The circle is denoted by C(O, r).
The fixed point O is called the centre and the constant distance r units is called its radius.
Results:
- If two circles touch internally, then the distance between their centers is equal to the difference of their radii.
- If two circles touch externally, then the distance between their centers is equal to the sum of their radii.
- Distance moved by a rotating wheel in one revolution is equal to the circumference of the wheel.
- Number of revolutions completed by a rotating wheel in one minute:
= Distance moved in one minute / Circumference
- Angle described by minute hand in one minute = 6°.
- Angle described by hour hand in one hour = 30°.
Circumferance:
The perimeter (or length of boundary) of a circle is called its circumference.
ARC:
A continuous piece of a circle is called an arc of the circle.
In the given figure, PQ is an arc of a circle, with centre O, denoted by PQ (with arc notation). The remaining part of the circle represents QP (with arc notation).
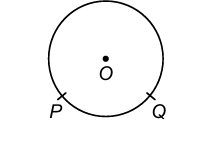
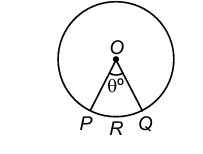
Central Angle:
An angle subtended by an arc at the centre of a circle is called its central angle.
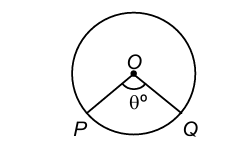
In the given figure of a circle with centre O, central angle of PQ (arc) = ∠POQ = θ°.
If θ° < 180° then the arc PQ is called the minor arc and the arc QP is called the major arc.
Semicircle:
A diameter divides a circle into two equal arcs. Each of these two arcs is called a semicircle.
In the given figure of a circle with centre O, PRQ (arc) and QSP (arc) are semicircles.
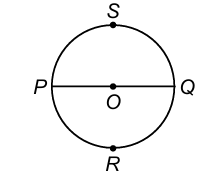
An arc whose length is less than the arc of a semicircle is called a minor arc. An arc whose length is more than the arc of a semicircle is called a major arc.
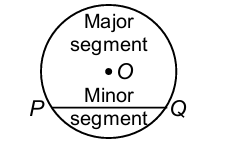
Segment:
A segment of a circle is the region bounded by an arc and a chord, including the arc and the chord.
The segment containing the minor arc is called a minor segment, while the segment containing the major arc is the major segment.
The centre of the circle lies in the major segment.
Sector of a Circle:
The region enclosed by an arc of a circle and its two bounding radii is called a sector of the circle.
In the given figure, OPRQO is a sector of the circle with centre O.
If arc PQ is a minor arc then OPRQO is called the minor sector of the circle.
The remaining part of the circle is called the major sector of the circle.
12.6
Quadrant:
One-fourth of a circular disc is called a quadrant. The central angle of a quadrant is 90°.
Formulae:
Circumference and area of a circle
For a circle of radius r, we have
- Circumference of the circle = 2πr
- Area of the circle = πr²
- Area of the semicircle = (1/2)πr²
- Perimeter of the semicircle = (πr + 2r)
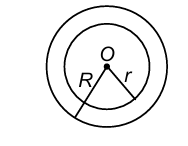
Area of a ring
Let R and r be the outer and inner radii of a ring.
Then, area of the ring = π(R² - r²)
Rotating wheels
- Distance moved by a wheel in 1 rotation = circumference of the wheel
- Number of rotations in 1 minute = (distance moved in 1 minute) / circumference
Rotation of the hands of a clock
- Angle described by the minute hand of a clock in 60 minutes = 360°
- Angle described by the hour hand of a clock in 12 hours = 360°
1. In figure, what is the ratio of the areas of a circle and a rectangle whose diameter and diagonal of a rectangle are respectively equal.
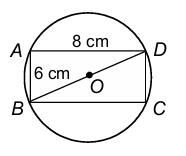
Sol. Diagonal of a rectangle = BD = √(6² + 8²) = 10 cm.
It is given that: diagonal of rectangle = diameter of a circle
∴ 10 = 2r ⇒ r = 5
∴ (Area of a circle of radius 5 cm) / (Area of a rectangle of sides 6 cm and 8 cm)
= (π × 5²) / (8 × 6) = 25π / 48
2. What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
Sol.
(Area of a circle of radius 'r') / (Area of an equilateral of sides 'a')
= πr² / ((√3/4)a²) = (4π/√3) × (r/a)² = (π/√3) × (2r/a)²
= π/√3 [∵ a = 2r]
3. The cost of fencing a circular field at the rate of Rs. 24 per metre is Rs. 5280. The field is to be ploughed at the rate of Rs. 0.50 per m². Find the cost of ploughing the field (Take π = 22/7).
Sol. Length of the fence = Total cost / Rate = 5280 / 24 = 220 m.
So, circumference of the field = 220 m.
Therefore, if r metres is the radius of the field,
∴ 2πr = 220 where r is the radius of field.
or 2 × (22/7) × r = 220
or r = (220 × 7) / (2 × 22) = 35 m
Therefore, area of the field = πr² = (22/7) × 35 × 35 = 22 × 5 × 35 m²
∴ cost of ploughing 1m² of the field = Rs. 0.50.
So, total cost of ploughing the field = Rs. 22 × 5 × 35 × 0.50 = Rs. 1925.
4. A circular park, 42 m in diameter, has a path 3.5 m wide running round it on the outside. Find the cost of gravelling the path at Rs. 4 per m².
Sol. Radius r of the circular park = 21 m.
Radius R of the outer circle = (21 + 3.5) m = 24.5 m
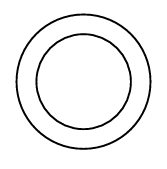
Area of the path = π[R² - r²]
= π[(24.5)² - (21)²]
= (22/7)(24.5 + 21)(24.5 - 21)
= (22/7) × 45.5 × 3.5 m² = 500.5 m²
∴ Cost of gravelling the path = Rs. (500.5 × 4) = Rs. 2002.
5. The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Sol. The area of the circle having radius 8 cm = π × (8)² (∵ r = 8 cm) = 64π cm².
The area of the circle having radius 6 cm = π × (6)² = 36π cm².
Sum of the areas of the two circles = (64π + 36π) cm² = 100π cm².
Let, if r be the radius of the circle which has area equal to the sum of the areas of the two given circles, then
πr² = 100π
∴ r² = 100
∴ r = 10
Hence, the required radius is 10 cm.
6. A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Sol. Distance covered by the wheel in 1 revolution
= (11 × 1000 × 100) / 5000 cm = 220 cm
∴ The circumference of the wheel = 220 cm.
Let the diameter of the wheel be d cm.
Then, πd = 220
⇒ (22/7) × d = 220
⇒ d = 220 × (7/22) = 70
Hence, the diameter of the wheel is 70 cm.
7. The diameter of the wheels of a bus is 140 cm. How many revolutions per minute must a wheel make in order to move at a speed of 66 km per hour?
Sol. Distance covered by a wheel in 1 minute
⇒ (66 × 1000 × 100) / 60 cm = 110000 cm
Circumference of a wheel
⇒ = (2 × (22/7) × 70) cm = 440 cm
Number of revolutions in 1 min
⇒ = (110000 / 440) = 250.
8. A steel wire, when bent in the form of a square, encloses an area of 121 sq cm. The same wire is bent in the form of a circle. Find the area of the circle.
Sol. Side of the square = √121 cm = 11cm
Perimeter of the square = (4 × 11) cm = 44 cm
∴ Length of the wire = 44 cm
∴ Circumference of the circle = Length of the wire = 44 cm
Let the radius of the circle be r cm
Then, 2πr = 44
⇒ 2 × (22/7) × r = 44
⇒ r = (110 × 7/22) m = 35 m.
∴ Area of the circle = πr²
= (22/7) × 7 × 7 cm² = 154 cm².
Area of Sector and Segment of a Circle
Length of arc, area of sector and segment
Let an arc AB make an angle θ° < 180° at the centre of a circle of radius r. Then, we have
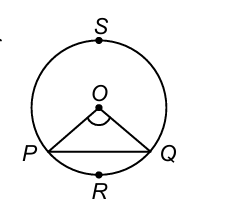
(i) Length of the arc PQ = (θ/360) × 2πr = ℓ
(ii) (a) Area of the sector OPRQO = (θ/360) × πr²
= (1/2) × (θ/360) × 2πr × r = (1/2) × ℓ × r
(b) Perimeter of the sector OPRQO = OP + OQ + length of arc PRQ
= 2r + (2πrθ/360)
(iii) (a) Area of the minor segment PRQP = (area of the sector OPRQO) – (area of △OPQ)
= (πr²θ/360) - (1/2)r² sin θ
(b) Area of the major segment QSPQ
= (area of the circle) – (area of the minor segment PRQP).
Worked Examples
1. If the following figure is a sector of circle of radius 10.5 cm. Find the perimeter of the sector.
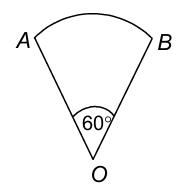
Sol. The arc length ℓ = AB of a sector of an angle 60° in a circle of radius 10.5 cm is given by
ℓ = (θ/360) × 2πr
⇒ ℓ = (60/360) × 2 × (22/7) × 10.5
⇒ ℓ = (1/6) × 3 × 22 = 11.
∴ Perimeter of sector OAB = OA + OB + arc AB = 10.5 + 10.5 + 11 = 32 cm.
2. In the following figure, the length of an arc AB = 20π cm is a sector of a circle, find the radius of the circle.
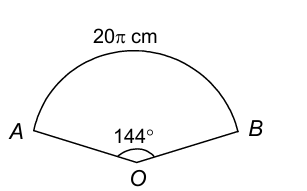
Sol. The arc of length AB = 20π cm of a sector of an angle 144° in a circle of radius r is given by
ℓ = (θ/360) × 2πr
⇒ 20π = (144/360) × 2πr
⇒ 20π = (2/5) × 2πr ⇒ r = 25 cm.
3. What is the ratio of the area of sector of angle 30° in a circle and that of the complete circle?
Sol. Area of a sector of angle 30° in a circle of radius r cm = (30°/360°) × πr² = πr²/12.
∴ (Area of a sector of angle 30° in a circle of radius r cm) / (Area of a circle of radius r cm)
= (πr²/12) / πr² = 1/12
Thus the ratio is 1 : 12.
4. An arc of a circle is of length 5π cm and the sector is bounds has an area 20 cm². Find the radius of the circle.
Sol. We know that
Area of a sector bounded by a given arc = (1/2) × (length of a given arc) × radius of a circle.
⇒ A = (1/2)ℓr ⇒ 20π = (1/2) × 5π × r
⇒ r = 40/5π = 8 cm.
5. The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
Sol. Angle described by the minute hand in 60 minutes = 360°.
Angle described by the minute hand in 35 minutes
= (360°/60) × 35 = 210° ⇒ θ = 210° and r = 12 cm
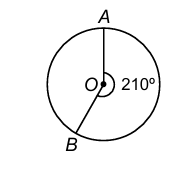
⇒ Area swept by the minute hand in 35 minutes
= (πr²θ/360) cm² = ((22/7) × 12 × 12 × 210/360) cm² = 264 cm².
6. The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.
Sol. Let O be the centre of a circle of radius 5.6 cm, and let OABO be its sector with perimeter 27.2 cm.
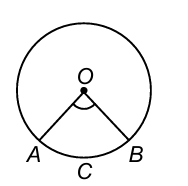
Then, OA + OB + arc AB = 27.2 cm
⇒ 5.6 cm + 5.6 cm + arc AB = 27.2 cm
⇒ arc AB = 16 cm.
Area of the sector OACBO
= (1/2) × radius × length of arc sq units
= (1/2) × 5.6 × 16 cm² = 44.8 cm².
7. An umbrella has 8 ribs, which are equally spaced (figure). Assume umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.
Sol. Here, r = 45° cm
θ = sector angle between two consecutive ribs
= 360°/8 [∵ There are 8 sectors of same size]
= 45°.
Therefore, the area between two consecutive ribs of the umbrella
= The area of one sector
= (1/2) × radius × length of arc sq units = (1/2) × 5.6 × 16 cm² = 44.8 cm².
AREAS OF COMBINATIONS OF PLANE FIGURES
In the previous section, we have learnt to find areas of sectors and segments of a circle. In this section, we will learn to calculate the areas of some plane figures which are combinations of more than one plane figure.
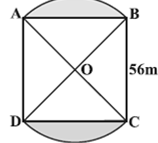
1. In the figure, two circular flowerbeds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flowerbed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flowerbeds.
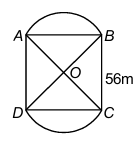
Sol. Area of the square lawn ABCD = (side)² = 56 × 56 m² ... (i)
Let OA = OB = x metres
In △AOB, ∠AOB = 90° [Diagonals of square bisect at 90°]
So, x² + x² = 56² [By Pythagoras theorem]
or, 2x² = 56 × 56
or, x² = 28 × 56 ... (ii)
Now, area of sector OAB = (90/360) × πx² = (1/4) × πx²
= (1/4) × (22/7) × 28 × 56 [From (ii)] ... (iii)
Also, area of △OAB = (1/2) × OA × OB = (1/2) × x²
= (1/2) × 28 × 56 [∠AOB = 90°] ... (iv)
So area of flower bed AB = area of sector OAB − area of △OAB
= (1/4) × (22/7) × 28 × 56 − (1/2) × 28 × 56 m²
= (1/4) × 28 × 56 × ((22/7) − 2) m² [From (iii) and (iv)]
= (1/4) × 28 × 56 × (8/7) m². ... (v)
Similarly, area of the other flower bed
= (1/4) × 28 × 56 × (8/7) m². ... (vi)
Therefore, total area
= 56 × 56 + (1/4) × 28 × 56 × (8/7) + (1/4) × 28 × 56 × (8/7) m²
= 28 × 56 × (2 + 2/7 + 2/7) m² [From (i), (v) and (vi)]
= 28 × 56 × (18/7) m² = 4032 m².
2. The inside perimeter of a running track, (figure) is 340 m. The length of each straight portion is 60 m, and the curved portions are semicircles. If the track is 7 m wide, find the area of the track. Also, find the outer perimeter of the track.
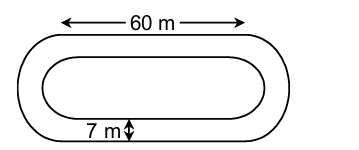
Sol. Length of inner curved portion = (340 – 2 × 60) m = 220 m.
∴ The length of each inner curved part = 110 m.
Let the radius of each inner curved part be r.
Then πr = 110 m ⇒ (22/7) × r = 110 m
⇒ r = (110 × 7/22) m = 35 m.
∴ Inner radius = 35 m, outer radius = (35 + 7) m = 42 m.
∴ Area of the track = (area of 2 rectangles) + (area of the circular ring)
= {(2 × 60 × 7) + (22/7) × [(42)² − (35)²]} m²
= [840 + (22/7) × (42 + 35)(42 − 35)] m²
= (840 + 1694) m² = 2534 m².
Length of the outer boundary of the track
= (2 × 60 + 2 × (22/7) × 42) m = 384 m.
Hence, the outer perimeter of the track is 384 m.
3. Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
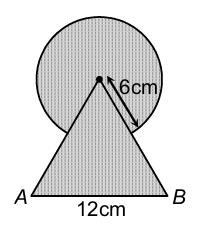
Sol. Area of the shaded region =
Area of the major sector of the circle + Area of the equilateral triangle OAB.
= [πr² − Area of the minor sector] + (√3/4) × (12)² [∵ Each side of the equilateral △ is 12 cm]
= [πr² − (60/360) × πr²] + 36√3 cm²
= (5/6) × πr² + 36√3 cm² = (5/6) × (22/7) × (6)² + 36√3 cm²
= [(5/6) × (22/7) × (6)² + 36√3] cm²
= (660/7 + 36√3) cm².
4. In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (π = 3.14).
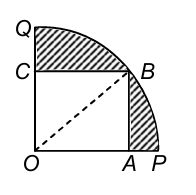
Sol. OB = √(OA² + AB²) = √((20)² + (20)²) = √800 = 20√2 cm.
Then for the quadrant OPBQ, r = 20√2 cm.
The area of the shaded region
= The area of the quadrant OPBQ – The area of the square OABC
= [(1/4) × π × (20√2)²] − (20)² cm²
= [(1/4) × 3.14 × 800] − 400 cm²
= [628 − 400] cm² = 228 cm².
5. On a square handkerchief, nine circular designs each of radius 7 cm are made (figure). Find the area of the remaining portion of the handkerchief.
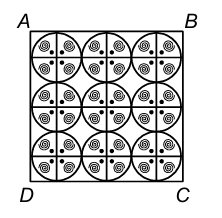
Sol. Radius of the circle = 7 cm
then diameter of the circle = 14 cm.
then length of the side of the square ABCD = 3 × 14 cm = 42 cm.
So, the total area of the handkerchief = (42)² cm² = 1764 cm².
Area of the nine circular designs = 9 × πr²
= 9 × (22/7) × (7)² cm² = 9 × 22 × 7 cm² = 1386 cm².
Then the required area of the remaining portion
= 1764 cm² − 1386 cm² = 378 cm²
6. Find the area of the shaded region in the figure, where ABCD is a square of side 14 cm.
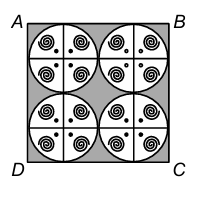
Sol. Area of square ABCD = 14 × 14 cm² = 196 cm².
Diameter of each circle = 14/2 cm = 7 cm,
So, radius of each circle = 7/2 cm.
So, area of one circle = πr² = (22/7) × (7/2) × (7/2) cm²
= 77/2 cm².
Therefore, area of the four circles = 4 × (77/2) cm² = 154 cm².
Hence, area of the shaded region = (196 – 154) cm² = 42 cm².
Area Related to Circle
Area of segment
(a) Area of the minor segment PRQP = (area of the sector OPRQO) – (area of △OPQ)
= (πr²θ/360) − (1/2)r² sin θ.
(b) Area of the major segment QSPQ
= (area of the circle) – (area of the minor segment PRQP).
Circumference and area of a circle
For a circle of radius r, we have
- Circumference of the circle = 2πr.
- Area of the circle = πr².
- Area of the semicircle = (1/2)πr²
- Perimeter of the semicircle = (πr + 2r).
Rotating wheels
- Distance moved by a wheel in 1 rotation = circumference of the wheel.
- Number of rotations in 1 minute = (distance moved in 1 minute) / circumference.
Rotation of the hands of a clock
- Angle described by the minute hand of a clock in 60 minutes = 360°.
- Angle described by the hour hand of a clock in 12 hours = 360°.
Length of arc, area of sector
Let an arc AB make an angle θ° < 180° at the centre of a circle of radius r. Then we have
- Length of the arc PQ = (2πrθ)/360 = ℓ.
- Area of the sector = (πr²θ)/360 = (1/2) × (2πrθ/360) × r = (1/2)ℓr.
- Perimeter of the sector = 2r + (2πrθ/360).
Area of a ring
Let R and r be the outer and inner radii of a ring.
Then area of the ring = π(R² − r²).
Circle:
The set of points which are at a constant distance of units from a fixed point O is called a circle with centre O and radius = r units. The circle is denoted by C(O, r).
The fixed point O is called the centre and the constant distance r units is called its radius.
Let's Try
Questions:
1. The cost of fencing a circular field at the rate of Rs 24 per metre is Rs 5280. The field is to be ploughed at the rate of Rs 0.50 per m². Find the cost of ploughing the field (π = 22/7).
2. Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14).
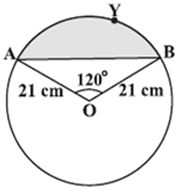
3. Find the area of the segment AYB shown in the figure, if the radius of the circle is 21 cm and ∠AOB = 120°. (Use π = 22/7).
4. In the Fig, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
Answers:
1. Rs. 1925, 2.(i) 4.19 cm² (approx.), (ii) 46.1 cm² 3. (21/4)(88 − 21√3)cm², 4. 4032m²
Detailed Solutions:
1. The cost of fencing a circular field at the rate of Rs 24 per metre is Rs 5280. The field is to be ploughed at the rate of Rs 0.50 per m². Find the cost of ploughing the field (π = 22/7).
Sol. Length of the fence (in meters) = Total cost / Rate = 5280 / 24 = 220
So circumference of the field = 220 m.
Therefore, if r metres is the radius of the field, then
2πr = 220
or, 2 × (22/7) × r = 220
or, r = (220 × 7) / (2 × 22) = 35 m.
i.e., radius of the field is 35m.
Therefore, area of the field = πr² = (22/7) × 35 × 35 m²
Now cost of ploughing 1m² of the field = Rs. 0.50
So Total cost of ploughing the field = Rs. 22 × 5 × 35 × 0.50 = Rs. 1925.
2. Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14).
Sol. Given sector is OAPB.
Area of the sector = (θ/360°) × πr²
= (30/360) × 3.14 × 4 × 4 cm²
= 12.56/3 cm² = 4.19 cm² (approx).
Area of the corresponding major sector
= πr² – area of sector OAPB
= (3.14 × 16 – 4.19) cm²
= 46.05 cm² = 46.1 cm² (approx.).
Alternatively, area of the major sector = ((360 − θ)/360) × πr² = ((360 − 30)/360) × 3.14 × 16 cm²
= (330/360) × 3.14 × 16 cm² = 46.05 cm² = 46.1 cm² (approx)
3. Find the area of the segment AYB shown in the figure, if the radius of the circle is 21 cm and ∠AOB = 120°. (Use π = 22/7).
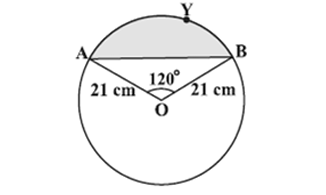
Sol. Area of the segment AYB
= Area of sector OAYB – Area of △OAB ...(i)
Now the area of the sector OAYB = (120/360) × (22/7) × 21 × 21cm² = 462 cm² ...(ii)
For finding the area of △OAB, draw OM ⊥ AB as shown in the figure.
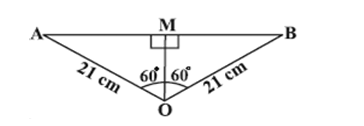
Now OA = OB. Therefore, by RHS congruence, △AMO ≅ △BMO.
So M is the mid-point of AB and ∠AOM = ∠BOM = (1/2) × 120° = 60°.
Let OM = x cm.
So from △OMA, cos 60° = OM/OA
or, x/21 = 1/2 (cos 60° = 1/2)
or, x = 21/2
So, OM = 21/2 cm
Also sin 60° = AM/OA = √3/2
So AM = (21√3)/2 cm.
Therefore, AB = 2AM = 2 × (21√3)/2 cm = 21√3 cm.
So area of △OAB = (1/2) × AB × OM = (1/2) × 21√3 × (21/2) cm² = (441√3)/4 cm² ...(iii)
Therefore, area of the segment AYB = 462 − (441√3)/4 cm² [From (i), (ii) and (iii)]
= (21/4)(88 − 21√3) cm².
5. Find the area of the shaded region in the fig. where ABCD is a square of side 14 cm.
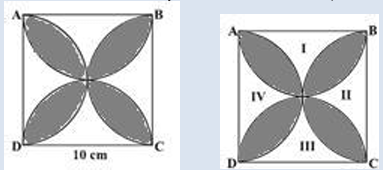
6. Find the area of the shaded design in the Fig, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. (Use π = 3.14)
7. A chord of circle 14 cm makes an angle of 60° at the center of the circle. Find:
- (i) area of minor sector
- (ii) area of the minor segment
- (iii) area of the major sector
- (iv) area of the major segment
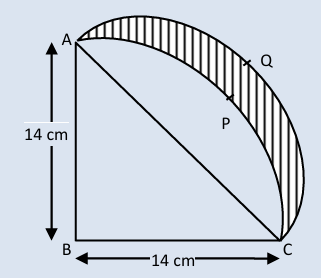
8. ABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semicircle is drawn. Find the area of the shaded portion.
Answers:
5. 42 cm², 6. 57 cm² 7. (i) 102.57 cm², (ii) 17.80 cm², (iii) 512.87 cm², (iv) 597.64 cm² 8. 98 cm²
5. Find the area of the shaded region in the Fig. where ABCD is a square of side 14 cm.
Sol. Area of square ABCD = 14 × 14 = 196 cm².
Diameter of each circle = 14/2 cm = 7 cm.
So, radius of each circle = 7/2 cm.
So, area of one circle = πr² = (22/7) × (7/2) × (7/2) cm² = 154/4 cm² = 77/2 cm².
Therefore, area of the four circles = 4 × (77/2) cm² = 154 cm².
Hence, area of the shaded region = (196 – 154)cm² = 42 cm².
6. Find the area of the shaded design in Fig, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. (Use π = 3.14)
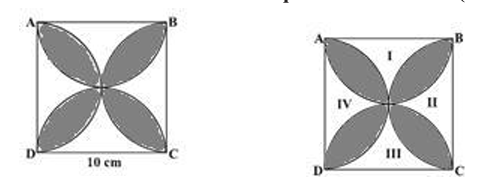
Sol. Mark the four unshaded regions as I, II, III and IV (figure)
area of I + area of III = area of ABCD – areas of two semicircles of each of radius 5 cm.
= [10 × 10 − 2 × (1/2) × π × 5²] cm² = (100 − 3.14 × 25) cm²
= (100 – 78.5)cm² = 21.5 cm².
Similarly, area of II + area of IV = 21.5 cm².
So area of the shaded design = area of ABCD – area of (I + II + III + IV)
= (100 – 2 × 21.5) cm² = (100 – 43) cm² = 57 cm².
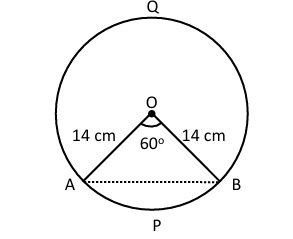
7. A chord of circle 14 cm makes an angle of 60° at the center of the circle. Find: (i) area of minor sector (ii) area of the minor segment (iii) area of the major sector (iv) area of the major segment
Sol. Given, r = 14 cm, θ = 60°.
[Circle showing chord AB, angle 60° at center O, radius 14 cm]
(i) Area of minor sector OAPB = (θ/360°) × πr²
= (60°/360°) × 3.14 × 14 × 14
= 102.57 cm².
(ii) Area of the minor segment APB = (πr²θ/360°) − (r²/2) sin θ
= 102.57 − (14 × 14/2) sin 60°
= 102.57 − 98 × (√3/2)
= 17.80 cm².
(iii) Area of the major sector
= area of circle – area of minor sector OAPB
= π (14)² – 102.57
= 615.44 – 102.57
= 512.87 cm².
(iv) Area of the major segment AQB
= area of Circle – area of minor segment APB
= 615.44 – 17.80
= 597.64 cm².
8. ABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semicircle is drawn. Find the area of the shaded portion.
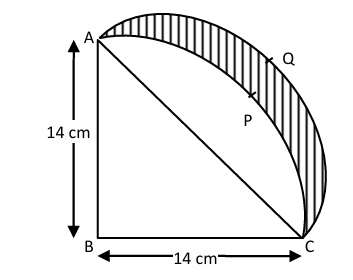
Sol. In right angles triangle ABC, we have,
AC² = AB² + BC²
AC² = 14² + 14²
AC = √(2 × 14²) = 14√2 cm.
Now required area = area APCQA
= area ACQA− area ACPA
= area ACQA – (area ABCPA – area of △ABC)
= (1/2) × π × (14√2/2)² − [(1/4) × π(14)² + (1/2) × 14 × 14]
= (1/2) × (22/7) × 7√2 × 7√2 − (1/4) × (22/7) × 14 × 14 + 7 × 14
= 154 – 154 + 98
= 98 cm².
Frequently Asked Questions
This chapter deals with:
-
Area of a sector of a circle
-
Area of a segment of a circle
-
Problems involving combinations of circles with squares, rectangles, triangles, etc.
-
Finding areas in practical situations like roads, flower beds, and wheel designs.
-
Sector: A region bounded by two radii and the arc between them.
-
Segment: A region bounded by a chord and the arc corresponding to it.
Area of minor segment=Area of sector−Area of triangle formed by radii and chord\text{Area of minor segment} = \text{Area of sector} - \text{Area of triangle formed by radii and chord}Area of minor segment=Area of sector−Area of triangle formed by radii and chor
Use π = 3.14 or π = 22/7 depending on the requirement of the problem. If not specified, either is acceptable.
- Finding the shaded region in a diagram involving circles.
-
Calculating the area of paths around circular fields.
-
Word problems involving circular objects like wheels, medals, or slices.