Mensuration

Easy Class 10 Mensuration Notes with Formulas and Examples

Class 10 Mensuration Notes offer a detailed study of surface areas, volumes, and related problem-solving techniques for different solids like cubes, cuboids, spheres, cones, and cylinders. These notes include formulas, solved examples, and practical tips to tackle mensuration problems efficiently. Understanding mensuration is essential for geometry, real-life applications, and exam preparation. The notes provide step-by-step methods to calculate surface area and volume accurately, along with shortcuts for faster computation. With practice exercises included, students can revise effectively and gain confidence in solving mensuration questions. These notes are an essential resource for Class 10 students aiming to strengthen their skills, improve problem-solving speed, and excel in board exams. Studnets must solve the NCERT questions with the help of the NCERT Solutions for class 10 Maths, which will help in building the foundation.

Class 10 Mensuration Notes, Solved example & Questions

Easy Class 10 Mensuration Notes with Formulas and Examples

Class 10 Mensuration Notes offer a detailed study of surface areas, volumes, and related problem-solving techniques for different solids like cubes, cuboids, spheres, cones, and cylinders. These notes include formulas, solved examples, and practical tips to tackle mensuration problems efficiently. Understanding mensuration is essential for geometry, real-life applications, and exam preparation. The notes provide step-by-step methods to calculate surface area and volume accurately, along with shortcuts for faster computation. With practice exercises included, students can revise effectively and gain confidence in solving mensuration questions. These notes are an essential resource for Class 10 students aiming to strengthen their skills, improve problem-solving speed, and excel in board exams. Studnets must solve the NCERT questions with the help of the NCERT Solutions for class 10 Maths, which will help in building the foundation.

Class 10 Mensuration Notes, Solved example & Questions

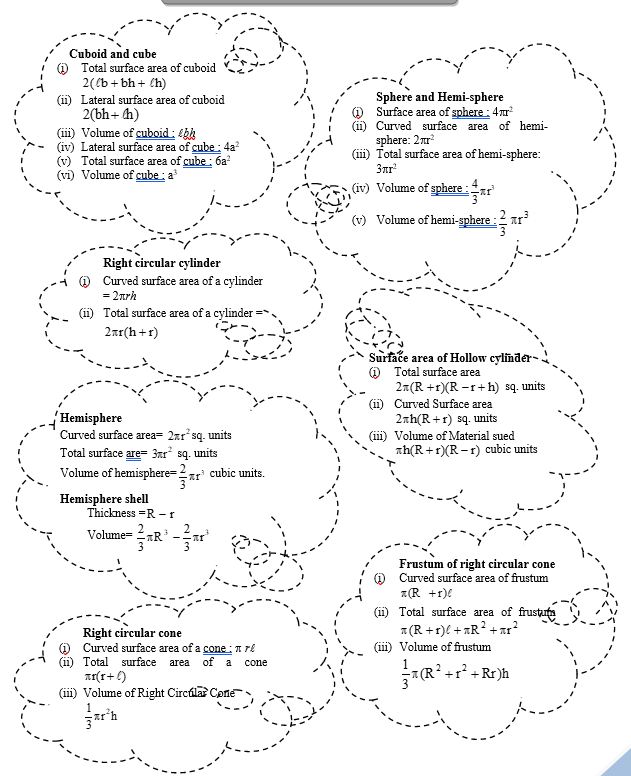
Any figure such as cuboid, which has three dimensions, viz. length, width and height is known as a three dimensional figure. Whereas rectangle has only two dimensions i.e. length and width. Three dimensional figures have volume in addition to areas of surfaces from which these solid figures are formed. Some of the main solid figures are:

Cuboid

Total surface Area (T.S.A.): The area of surface from which cuboid is formed. There are six faces (rectangular), eight vertices and twelve edges in a cuboid.

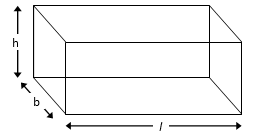
(i) Total surface Area (T.S.A.) = 2 [l × b + b × h + h × l]

(ii) Lateral Surface Area (L.S.A) = 2 [b × h + h × l]
(or Area of 4 walls) = 2h [l + b]

(iii) Volume of Cuboid = (Area of base) × height = (l × b) × h

(iv) Length of diagonal = √(l² + b² + h²)

Cube

Cube has six faces. Each face is a square.

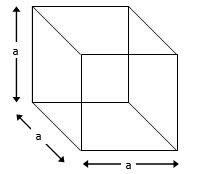
(i) T.S.A. = 2 [a × a + a × a + a × a]
= 2[a² + a² + a²]
= 2(3a²)
= 6a²

(ii) L.S.A. = 2[a² + a²]
= 4a²

(iii) Volume = (Area of base) × Height
= (a²) × a = a³

(iv) Length of altitude = √3a

Also Read: Arithmetic Progressions Notes

Cylinder

A cylinder (from Greek κύλινδρος – kulindros, "roller, tumbler") is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder.

Surface Area of a Right Circular Cylinder

Curved surface Area (C.S.A.): It is the area of surface from which the cylinder is formed. When we cut this cylinder, we will find a rectangle with length 2πr and height h units.

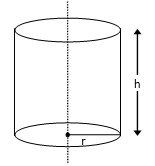
CSA = 2πrh

where r = radius of base
h = height of cylinder

Total Surface Area of a Cylinder:

= 2πrh + 2πr²
= 2πr(h + r) sq. units

where r = radius of base
h = height of cylinder

Volume of Cylinder:

V = πr²h cubic units

where r = radius of base
h = height of cylinder

Surface Area of Hollow Cylinder

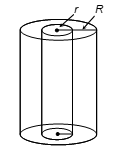
1. Curved surface area = 2πRh + 2πrh = 2πh(R + r) sq. units

2. Total surface area = 2πh(R + r) + 2π(R² − r²)
= 2π(R + r)(R − r + h) sq. units

3. Volume of material used = πR²h − πr²h
= πh(R + r)(R − r) cubic units

Cone

A cone is an n-dimensional geometric shape that tapers smoothly from a base (usually flat and circular) to a point called the apex or vertex.

Surface Area of a Right Circular Cone

Curved Surface Area of a Cone:

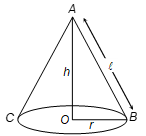
C = πrℓ

where:
C = curved surface area
r = radius of base of cone
ℓ = slant height

ℓ = √(h² + r²)

Total Surface Area of a Cone:

T = πrℓ + πr²
= πr(r + ℓ)

where:
T = total surface area
r = radius of base of cone
ℓ = slant height of cone

Must Read: Quadratic Equations Notes

Volume of Right Circular Cone:

V = (1/3)πr²h cubic units

where:
V = volume of cone
r = radius of base of cone
h = height of cone

Sphere

A sphere (from Greek σφαῖρα — sphaira, "globe, ball") is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle, which is in two dimensions, a sphere is the set of points which are all the same distance r from a given point in space. This distance r is known as the "radius" of the sphere, and the given point is known as the center of the sphere. The maximum straight distance through the sphere is known as the "diameter". It passes through the center and is thus twice the radius.

Surface area of a sphere = 4πr² sq. units

Volume of a sphere = (4/3)πr³ sq. units

Spherical Shell / Hollow Sphere

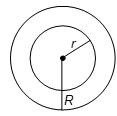
1. Thickness = R − r

2. Volume = (4/3)πR³ − (4/3)πr³ cubic units

Hemisphere

A half of a sphere is known as hemisphere.

Curved surface area = 2πr²

Total surface area = C.S.A. + other area
= 2πr² + πr²
= 3πr²

Volume = (2/3)πr³

Hemisphere Shell

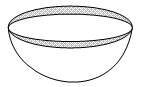
Thickness = R − r

Volume = (2/3)πR³ − (2/3)πr³

Frustum of a Cone

When a cone is cut by a plane parallel to base, a small cone is obtained at top and other part is obtained at bottom. This is known as 'Frustum of Cone'.

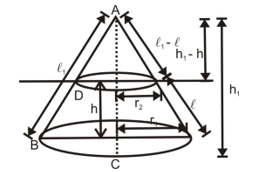
△ABC ~ △ADE

AC/AE = AB/AD = BC/DE

h₁/(h₁ − h) = r₁/r₂

Or h₁/h = ℓ₁/(ℓ₁ − ℓ) = r₁/(r₁ − r₂)

Volume of Frustum:

= (1/3)πr₁²h₁ − (1/3)πr₂²(h₁ − h)

= (1/3)πh[r₁² + r₂² + r₁r₂]

Curved Surface Area of Frustum:

= πr₁ℓ₁ − πr₂(ℓ₁ − ℓ)

= πℓ(r₁ + r₂)

Total Surface Area of Frustum:

= CSA of frustum + πr₁² + πr₂²

= πℓ(r₁ + r₂) + πr₁² + πr₂²

Also Read: Statistics Notes

Slant height of a Frustum:

ℓ = √[h² + (r₁ − r₂)²]

where:
h = height of the frustum
r₁ = radius of larger circular end
r₂ = radius of smaller circular end

Solved Examples

Example 1

The decorative block is made of two solids – a cube and a hemisphere. The base of the block is a cube with edge 5 cm and the hemisphere fixed on the top has a diameter of 4.2 cm, find the total surface area of the block. (Take π = 22/7)

Solution:

The total surface area of the cube = 6 × (edge)² = 6 × 5 × 5 cm² = 150 cm²

The part of the cube where the hemisphere is attached is not included in the surface area.

So, the surface area of the block = TSA of cube – base area of hemisphere + CSA of hemisphere

= 150 − πr² + 2πr² = (150 + πr²) cm²

= 150cm² + (22/7) × (4.2/2) × (4.2/2) cm²

= (150 + 13.86) cm² = 163.86 cm²

Example 2

A wooden toy rocket is in the shape of a cone mounted on a cylinder. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)

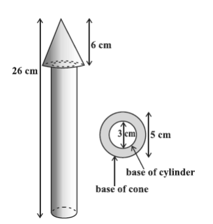
Solution:

The radius of cone is denoted by r, slant height of cone by l, height of cone by h, radius of cylinder by r′ and height of cylinder by h′.

Then r = 2.5 cm, h = 6 cm, r′ = 1.5 cm, h′ = 26 – 6 = 20 cm

l = √(r² + h²) = √((2.5)² + 6²) cm = √42.25 cm = 6.5 cm

Here, the conical portion has its circular base resting on the base of the cylinder, but the base of the cone is larger than the base of the cylinder. So, a part of the base of the cone (a ring) is to be painted.

So, the area to be painted orange = CSA of the cone + base area of the cone – base area of the cylinder

= πrl + πr² − π(r')²

= π[(2.5 × 6.5) + (2.5)² − (1.5)²] cm²

= π[20.25] cm² = 3.14 × 20.25 cm² = 63.585 cm²

Now, the area to be painted yellow = CSA of the cylinder + area of one base of the cylinder

= 2πr'h' + π(r')²

= πr'(2h' + r')

= (3.14 × 1.5)(2 × 20 + 1.5) cm² = 4.71 × 41.5 cm² = 195.465 cm²

Example 3

Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder. If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m³, and there are 20 workers, each of whom occupy about 0.08 m³ space on an average. Then, how much air is in the shed?

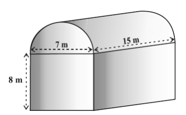
Solution:

The volume of air inside the shed (when there are no people or machinery) is given by the volume of air inside the cuboid and inside the half cylinder, taken together.

Now, the length, breadth and height of the cuboid are 15 m, 7 m and 8 m, respectively.

Also, the diameter of the half cylinder is 7 m and its height is 15 m.

So, the required volume = volume of the cuboid + (1/2) × volume of the cylinder

= [15 × 7 × 8 + (1/2) × (22/7) × (7/2) × (7/2) × 15] m³ = 1128.75 m³

Next, the total space occupied by the machinery = 300 m³

And the total space occupied by the workers = 20 × 0.08 m³ = 1.6 m³

Therefore, the volume of the air, when there are machinery and workers

= 1128.75 – (300.00 + 1.60) = 827.15 m³

Also Read: Probability Notes

Example 4

A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)

Solution:

Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere.

The radius BO of the hemisphere (as well as of the cone) = (1/2) × 4 cm = 2 cm

So, Volume of the toy = (2/3)πr³ + (1/3)πr²h

= [(2/3) × 3.14 × (2)³ + (1/3) × 3.14 × (2)² × 2] cm³ = 25.12 cm³

Now, let the right circular cylinder EFGH circumscribe the given solid.

The radius of the base of the right circular cylinder = HP = BO = 2 cm

and its height is EH = AO + OP = (2 + 2) cm = 4 cm

So, the volume required = volume of the right circular cylinder – volume of the toy

= (3.14 × 2² × 4 – 25.12) cm³ = 25.12 cm³

Hence, the required difference of the two volumes = 25.12 cm³

Example 5

A cone of height 24 cm and radius of base 6 cm is made up of modeling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.

Solution:

Volume of cone = (1/3) × π × 6² × 24 cm³

If r is the radius of the sphere, then its volume is (4/3)πr³

Since, the volume of clay in the form of the cone and the sphere remains the same, we have

(4/3)πr³ = (1/3) × π × 6² × 24

i.e., r³ = 3 × 3 × 24 = 3² × 2³

So, r = 3 × 2 = 6

Therefore, the radius of the sphere is 6 cm.

Example 6

Selvi's house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)

Solution:

The volume of water in the overhead tank equals the volume of the water removed from the sump.

Now, the volume of water in the overhead tank (cylinder) = πr²h = 3.14 × 0.6 × 0.6 × 0.95 m³

The volume of water in the sump when full = l × b × h = 1.57 × 1.44 × 0.95 m³

The volume of water left in the sump after filling the tank

= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 × 0.95)] m³

= (1.57 × 1.44 × 0.95) m³

So, the height of the water left in the sump = (volume of water left in the sump)/(l × b)

= [(1.57 × 0.6 × 0.6 × 0.95 × 2)/(1.57 × 1.44)] m = 0.475 m = 47.5 cm

Also, capacity of tank / capacity of sump = (1.57 × 1.44 × 0.95)/(3.14 × 0.6 × 0.6 × 0.95) = 1/2

Therefore, the capacity for the tank is half the capacity of the sump.

Example 7

A hemispherical tank full of water is emptied by a pipe at the rate of 3(4/7) litres per second. How much time will it take to empty half the tank, if it is 3m in diameter? (Take π = 22/7)

Solution:

Radius of the hemispherical tank = 3/2 m

Volume of the tank = (2/3) × (22/7) × (3/2)³ m³ = 99/14 m³

So, the volume of the water to be emptied = (1/2) × (99/14) m³ = (99/28) m³ = (99/28) × 1000 litres = 99000/28 litres

Since, 25/7 liters of water is emptied in 1 second, 99000/28 liters of water will be emptied in (99000/28) × (7/25) seconds, i.e., in 16.5 minutes.

Example 8

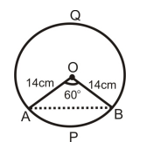
A chord of circle 14 cm makes an angle of 60° at the center of the circle. Find:

(i) area of minor sector

(ii) area of the minor segment

(iii) area of the major sector

(iv) area of the major segment

Solution:

Given, r = 14 cm, θ = 60°

(i) Area of minor sector OAPB = (θ/360°) × πr²

= (60°/360°) × 3.14 × 14 × 14 = 102.57 cm²

(ii) Area of minor segment APB = (πr²θ/360°) − (r²/2) sin θ

= 102.57 − (14 × 14/2) sin 60°

= 102.57 − 98 × (√3/2) = 17.80 cm²

(iii) Area of major sector = Area of circle - Area of minor sector OAPB

= π(14)² – 102.57 = 615.44 – 102.57 = 512.87 cm²

(iv) Area of major segment AQB = Area of circle - Area of minor segment APB

= 615.44 – 17.80 = 597.64 cm²

Example 9

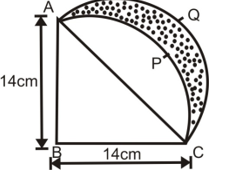
ABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semicircle is drawn. Find the area of the shaded portion.

Solution:

In right angled triangle ABC, we have:

AC² = AB² + BC²

AC² = 14² + 14²

AC = √(2 × 14²) = 14√2 cm

Now required Area = Area APCQA

= Area ACQA – Area ACPA

= Area ACQA - (Area ABCPA - Area of △ABC)

= (1/2) × π × (14√2/2)² − [(1/4) × π(14)² + (1/2) × 14 × 14]

= (1/2) × (22/7) × 7 × √2 × 7 × √2 − (1/4) × (22/7) × 14 × 14 + 7 × 14

= 154 – 154 ÷ 98 = 98 cm²

Example 10

The diameter of cycle wheel is 28 cm. How many revolution will it make in moving 13.2 km?

Solution:

Distance traveled by the wheel is one revolution = 2πr

= 2 × (22/7) × (28/2) = 88 cm

and the total distance covered by the wheel = 13.2 × 1000 × 100 cm = 1320000 cm

∴ Number of revolution made by the wheel = 1320000/88 = 15000

Conversion of Solid from One Shape to Another

For commercial works and for industrial development work, we need to convert a solid into another solid of different shape or more than one solid of similar shape but with reduced size. The calculation of surface areas and volumes in above cases will be illustrated below.

Example 1

A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?

Solution:

Let r be the radius of a cylinder, a cone and a hemisphere respectively and h be the height of the cylinder, a cone and a hemisphere respectively.

Then, h = r

V₁ = Volume of a cylinder = πr²h

V₂ = Volume of a cone = (1/3)πr²h

V₃ = Volume of a hemisphere = (2/3)πr³

V₁ : V₂ : V₃ = πr²h : (1/3)πr²h : (2/3)πr³

V₁ : V₂ : V₃ = 3h : h : 2r [∵ r = h in case of hemisphere]

⇒ V₁: V₂: V₃ = 3:1:2

Example 2

A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, find the radius of the base of the cone.

Solution:

Volume of a solid sphere of radius r = Volume of cone of base r₁ and height r

(4/3)πr³ = (1/3)πr₁²(r)

⇒ 4r² = r₁²

⇒ r₁ = 2r

Thus, the radius of the base of the cone is 2r.

Example 3

A metallic sphere of radius 10.5 cm is melted and then recast into smaller cones, each of radius 3.5 cm and height 3 cm. How many cones are obtained?

Solution:

Radius of the sphere = 21/2 cm

Volume of the sphere = (4/3)π(21/2)³ cm³ = (3087π/2) cm³

Radius of each cone = 7/2 cm and its height = 3 cm

Volume of each cone = (1/3)π(7/2)² × 3 cm³ = (49π/4) cm³

Required number of cones = volume of the sphere / volume of each cone

= (3087π/2) × (4/49π) = 126

Example 4

The internal and external radii of a hollow sphere are 3 cm and 5 cm respectively. The sphere is melted to form a solid cylinder of height 2(2/3) cm. Find the diameter and the curved surface area of the cylinder.

Solution:

External radius of the sphere = 5 cm

Internal radius of the sphere = 3 cm

Volume of metal in the hollow sphere = (4/3)π(R³ − r³) = (4/3)π[(5)³ − (3)³] = (392π/3) cm³

Let the radius of the solid cylinder be r cm.

Height of the solid cylinder = 8/3 cm

Volume of the solid cylinder = πr² × (8/3) cm³

Volume of cylinder = Volume of metal in hollow sphere

∴ πr² × (8/3) = 392π/3

⇒ r² = 49 ⇒ r = 7

Hence, the diameter of the cylinder formed = (2×7) cm = 14 cm

Curved surface area of the cylinder = 2πrh = 2 × (22/7) × 7 × (8/3) cm²

= 352/3 cm² = 117(1/3) cm²

Example 5

A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere and total height of the toy, if the height of the cone is 3 times the radius.

Solution:

Radius of the cylinder = 6 cm

Height of the cylinder = 15 cm

Volume of the cylinder = π × 6 × 6 × 15 cm³ = 540π cm³

Volume of 12 toys = 540π cm³

Volume of 1 toy = (540π/12) cm³ = 45π cm³

Let the radius of the hemisphere be r cm.

Then, the height of the cone = 3r cm

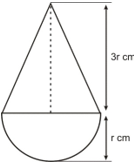
Volume of 1 toy = volume of hemisphere + volume of cone

= (2/3)πr³ + (1/3)πr²(3r) cm³ = (5πr³/3) cm³

∴ (5πr³/3) = 45π

⇒ r³ = 27 = 3³

⇒ r = 3

Radius of the hemisphere = 3 cm

Total height of the toy = (r + 3r) cm = (4r) cm = (4× 3) cm = 12 cm

Example 6

A well, whose diameter is 7m, has been dug 22.5 m deep and the earth dugout is used to form an embankment around it. If the height of the embankment is 1.5m, find the width of the embankment.

Solution:

Radius of the well = 7/2 m = 3.5 m

Depth of the well = 22.5 m

∴ Volume of the earth dugout = π × (7/2) × (7/2) × (45/2) m³

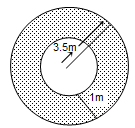
Let the width of the embankment be r metres.

Embankment forms a cylindrical shell whose inner and outer radii are 3.5 m and (r + 3.5) m respectively and height 1.5 m.

∴ Volume of the embankment = π[(r + 3.5)² − (3.5)²] × 1.5 m³ = (3π/2)r(r + 7) m³

But, Volume of the embankment = Volume of the earth dugout

∴ (3π/2)r(r + 7) = π × (7/2) × (7/2) × (45/2)

⇒ r(r + 7) = 49/4 × 15

⇒ 4r² + 28r = 735

⇒ 4r² + 28r − 735 = 0

⇒ r = [−28 ± √(784 + 11760)]/8

= [−28 ± √12544]/8 = [−28 ± 112]/8 = 84/8 = 10.5 [∵ r > 0]

Hence, the width of the embankment is 10.5 m.

Mensuration

Illustrations

Problem 1

If two cones have their volumes in the ratio 3:1 and their heights are in the ratio 1:3, then find the ratio of their radius.

Solution:

V₁/V₂ = [(1/3)πr₁²h₁] / [(1/3)πr₂²h₂]

= (r₁/r₂)² × (h₁/h₂) = 3/1 = (r₁/r₂)² × (1/3)

⇒ (3/1)² = (r₁/r₂)²

⇒ r₁/r₂ = 3/1

Thus the ratio of their radius is 3:1.

Problem 2

The height and base of cone, each is increased by 100%. What is the ratio between the volume of a given cone and new cone?

Solution:

Given volume of cone [V₁] = (1/3)πr²h

Increased height = h + 100% of h

= h + (100h/100) = 2h

Similarly increased radius = 2r

∴ Volume of new cone [V₂] = (1/3)π(2r)²(2h)

= 8 × (1/3)πr²h

V₁/V₂ = [(1/3)πr²h] / [8 × (1/3)πr²h] = 1/8

Problem 3

Three cubes each of side 5 cm are joined end to end. Find the surface area of the resulting cuboid.

Solution:

Given three cubes I, II and III each of side 5 cm are joined end to end. The resulting solid becomes a rectangular cuboid having dimensions 15 cm × 5 cm × 5 cm.

Surface area = 2[15×5 + 5×5 + 5×15] cm²

= 2[75 + 25 + 75] cm² = 350 cm²

Problem 4

A solid is made up of a cube and a hemisphere attached on its top, as shown in the figure. Each edge of the cube measures 5 cm and the hemisphere has a diameter of 4.2 cm. Find the total area to be painted (Take π = 22/7).

Solution:

Total surface area of the cube = 6 × (edge)²

= (6 × 5 × 5) cm² = 150 cm²

Area to be painted = (total surface area of the cube) − (base area of the hemisphere) + (curved surface area of the hemisphere)

= (150 − πr² + 2πr²) cm²

= (150 + πr²) cm²

= 150 + (22/7) × 2.1 × 2.1 cm²

= 150 + 693/50 cm²

= (150 + 13.86) cm² = 163.86 cm²

Problem 5

A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed into the tub. If the radius of the hemisphere is 3.5 cm and the height of the cone outside the hemisphere is 5 cm, find the volume of water left in the tub. (Take π = 22/7).

Solution:

Volume of water in the cylindrical tub = volume of the tub

= πr²h = (22/7) × 5 × 5 × 9.8 cm³ = 770 cm³

Volume of the solid immersed in the tub = (2/3)πr³ + (1/3)πr²h

= (2/3) × (22/7) × (7/2) × (7/2) × (7/2) + (1/3) × (22/7) × (7/2) × (7/2) × 5 cm³

= (539/6 + 385/6) cm³ = (924/6) cm³ = 154 cm³

Volume of water left in the tub = (volume of the tub) – (volume of solid immersed in the tub)

= (770 – 154) cm³ = 616 cm³

Problem 6

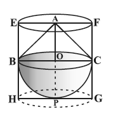
A right triangle, whose sides are 15 cm and 20 cm, is made to revolve about its hypotenuse. Find the volume and the surface area of the double cone so formed. (Take π = 3.14)

Solution:

△ABC is right angled at C, i.e., ∠BCA = 90°

Its sides AC and BC are of lengths, 20 cm and 15 cm respectively.

AB = √[(20)² + (15)²] cm = 25 cm is the hypotenuse.

The double cone is formed as shown in the figure.

△BOC and △BCA are similar.

⇒ BO/BC = CO/AC = BC/BA = 15/25

⇒ CO/20 = 15/25 and BO/15 = 15/25

⇒ CO = 12 cm and BO = 9 cm

Then AO = 25 cm – 9 cm = 16 cm

The two right circular cones have common base and base-radius = CO = C'O = 12 cm

Their vertices are at A and B

height of one cone is AO = 16 cm and that of the second cone is BO = 9 cm

Their slant heights are AC = 20 cm and BC = 15 cm respectively.

The volume of the double cone = The sum of the volumes of the two cones

= (1/3)π(12)²(16) + (1/3)π(12)²(9) cm³

= (1/3)π(12)²(16 + 9) cm³

= (1/3) × 3.14 × 144 × 25 cm³ = 3768 cm³

The surface area of the double cone = The sum of the curved surface areas of the two cones

= π(12)(20) + π(12)(15) cm²

= π(12)(20 + 15) cm²

= 3.14 × 12 × 35 cm² = 1318.8 cm²

Problem 7

The diameter of a copper sphere is 6 cm. The sphere is melted and drawn into a long wire of uniform circular cross section. If the length of the wire is 36 cm, find its radius.

Solution:

Radius of the sphere = 3 cm

Volume of the sphere = (4/3)πr³ = (4/3)π × 3 × 3 × 3 cm³ = (36π) cm³

Length (height) of wire = 36 cm

Let the radius of the wire be r cm.

Volume of the wire = (πr²h) cm³ = (πr² × 36) cm³

But, volume of wire = volume of sphere

⇒ 36πr² = 36π

⇒ r² = 1

⇒ r = 1

Hence, the radius of the wire is 1 cm.

Problem 8

A cylindrical container of radius 6 cm and height 15 cm is filled with ice cream. The whole ice cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, find the radius of the ice-cream cone.

Solution:

Radius of the cylinder, r = 6 cm

Height of the cylinder, h = 15 cm

Volume of ice cream in the cylinder = (πr²h) = (π × 6 × 6 × 15) cm = (540π) cm³

Volume of ice cream given to each child = (540π/10) cm³ = (54π) cm³

∴ Volume of each cone = (54π) cm³

Let the radius of the base of the cone be r cm.

Then, height of the conical part = (4r) cm

Volume of the conical portion = (1/3)πr²(4r) cm³ = (4πr³/3) cm³

Volume of the hemispherical portion = (2/3)πr³ cm³

Volume of each ice-cream cone = (volume of conical part + volume of hemispherical part)

= (4πr³/3) + (2πr³/3) cm³ = (2πr³) cm³

∴ 2πr³ = 54π

⇒ r³ = 27 = 3³

⇒ r = 3

Hence the radius of the ice-cream cone = 3 cm.

Problem 9

Water flows through a circular pipe whose internal diameter is 2 cm, at the rate of 0.7 m per second into a cylindrical tank, the radius of whose base is 40 cm. By how much will the level of water rise in the tank in half an hour?

Solution:

Internal radius of the circular pipe = 1 cm

Length of water that flows in 30 min = (0.7 × 100 × 60 × 30) cm = 126000 cm

Volume of water that flows in 30 min = πr²h = (π × 1 × 1 × 126000) cm³ = (126000π) cm³

Radius of the base of cylindrical tank = 40 cm

Let the depth of water in the tank be x cm.

Volume of water in the tank = πr²H = (π × 40 × 40 × x) cm³

Volume of water in the tank = volume of water flow through the pipe

⇒ π × 40 × 40 × x = 126000π

⇒ x = 126000/(40 × 40) = 315/4 = 78.75

Hence, rise in level = 78.75 cm.

Problem 10

A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm³ of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. (Take π = 22/7).

Solution:

Here R = 20 cm, r = 12 cm and volume = 12308.8 cm³

Let the height of the bucket be h cm.

Volume of the bucket = Volume of frustum of the cone

(1/3)πh(R² + r² + Rr) = 12308.8

⇒ (1/3) × 3.14 × h[(20)² + (12)² + 20 × 12] = 12308.8 cm³

⇒ 784h = (12308.8 × 3)/3.14

⇒ h = (12308.8 × 3)/(3.14 × 784) = 15

Slant height of the bucket ℓ = √[h² + (R − r)²] sq. units

= √[(15)² + (20 − 12)²] cm

= √(225 + 64) = √289 cm = 17 cm

Area of the metal sheet used = (curved surface area) + (area of the bottom)

= [πℓ(R + r) + πr²] sq. units

= 3.14 × 17(20 + 12) + 3.14 × 12 × 12] cm²

= 3.14(544 + 144) cm²

= (3.14 × 688) cm² = 2160.32 cm²

Problem 11

The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 1/27 of the volume of the given cone, at what height above the base is the section made?

Solution:

Height of the given cone = 30 cm

Let the radius of its base be R cm.

Volume of the given cone = (1/3)πR² × 30 = (10πR²) cm³

Then volume of the smaller cone = (1/3)πr²h cm³

∴ (1/3)πr²h = (1/27)(10πR²) [given]

⇒ (R/r)² = 9h/10 ... (i)

Now, △OAB ~ △OCD

∴ AB/CD = OA/OC = R/r = 30/h ... (ii)

From (i) and (ii), we get

(30/h)² = 9h/10

⇒ (30 × 30)/(h × h) = 9h/10

⇒ h³ = (30 × 30 × 10)/9 = 1000

⇒ h³ = (10)³ ⇒ h = 10

⇒ Height of the smaller cone = 10 cm

Height of the section from the base = (30 – 10) cm = 20 cm

Problem 12

A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.

Solution:

Let the radius of both cone and hemisphere be r cm.

Let h be the height of the cone.

It is given that: Volume of a cone = Volume of a hemisphere

⇒ (1/3)πr²h = (2/3)πr³

⇒ h = 2r ⇒ h/r = 2/1

⇒ h:r = 2:1, i.e., the ratio of the heights of a cone and hemisphere is 2:1.

Problem 13

If the surface areas of two spheres are in the ratio 4:9, what will be the ratio of their volumes?

Solution:

S₁/S₂ = 4/9

⇒ 4πr₁²/4πr₂² = 4/9

⇒ r₁²/r₂² = 4/9

⇒ r₁/r₂ = 2/3

∴ V₁/V₂ = [(4/3)πr₁³]/[(4/3)πr₂³] = (r₁/r₂)³ = (2/3)³ = 8/27

Problem 14

If each of the length, breadth and height of a cuboid is doubled, then what is the total surface area of the new cuboid?

Solution:

Given surface area [S₁] = 2[lb + bh + hl]

Increased length = 2l

Increased breadth = 2b

Increased height = 2h

Changed surface area [S₂] = 2[2l × 2b + 2b × 2h + 2h × 2l]

= 2 × 4[lb + bh + hl]

⇒ S₂ = 4[S₁]

Problem 15

A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of its hemispherical end is 7 cm, find the cost of polishing its surface at the rate of Rs. 10 per dm².

Solution:

Radius of each hemispherical end = 7 cm

Height of each hemispherical part = its radius = 7 cm

Height of the cylindrical part = (104 – 2 × 7) cm = 90 cm

Area of surface to be polished = 2 (curved surface area of the hemisphere) + (curved surface area of the cylinder)

= [2(2πr²) + 2πrh] sq units

= 2πr(2r + h) cm²

= 2 × (22/7) × 7((2 × 7) + 90) cm²

= (44 × 104) cm² = 4576 cm²

= (4576)/(10 × 10) dm² = 45.76 dm² [∵ 10cm = 1dm]

Cost of polishing at the rate of Rs. 10 per dm² = 10 × 45.76 = Rs. 457.60

Problem 16

A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.

Solution:

The shape of the toy is as given:

Radius of the hemisphere = 5 cm

Radius of the base of the cylinder = 5 cm

Radius of the base of the cone = 5 cm

Height of the hemisphere = its radius = 5 cm

Let the height of the cone be h cm.

Then, (5+13+h) cm = 30 cm ⇒ h = 12

∴ Height of the cone = 12 cm

Slant height of the cone, ℓ = √[5² + (12)²] cm = √169 cm = 13 cm

Surface area of the toy = curved surface area of the hemisphere + curved surface area of the cylinder + curved surface area of the cone

= (2πr² + 2πrh + πrℓ) sq units

= [(2π(5)² + 2π × 5 × 13 + π × 5 × 13] cm²

= (22/7) × 245 cm² = 770 cm²