Trigonometry

Detailed Class 10 Trigonometry Notes for Easy Understanding

Class 10 Trigonometry Notes provide a detailed study of trigonometric ratios, identities, and applications in solving angles and triangles. These notes cover sine, cosine, tangent, cotangent, secant, cosecant, and fundamental identities, along with stepwise examples and practice problems. Students can learn techniques for solving height and distance problems, angle calculations, and verifying trigonometric identities. Understanding trigonometry is vital for geometry, coordinate geometry, and real-life applications like construction, physics, and engineering. After reading the note, solving NCERT questions with the help of the NCERT Solutions for class 10 Maths will help in building the foundation. Maths notes also offer tips for solving questions quickly, remembering formulas, and avoiding common errors. Class 10 students can use these notes for structured learning, revision, and exam preparation, ensuring confidence in tackling trigonometry questions effectively.

Class 10 Trigonometry Notes, Solved example & Questions

Trigonometry derives from the Greek words 'tri' (three), 'gonia' (angle), and 'metron' (measure), literally meaning the measurement of three angles. This branch of mathematics focuses on the relationships between the sides and angles of triangles, particularly right-angled triangles. The fundamental concepts of trigonometry are essential for understanding wave mechanics, circular motion, oscillations, and countless real-world applications in physics, engineering, and architecture.

Systems of Angle Measurement

Before working with trigonometric ratios, understanding how angles are measured is crucial. Three primary systems exist:

Sexagesimal System: The most common system divides a right angle into 90 equal parts called degrees (°). Each degree subdivides into 60 minutes ('), and each minute into 60 seconds ("). This system's prevalence in navigation and surveying stems from ancient Babylonian mathematics.

Centesimal System: This decimal-based system divides a right angle into 100 grades (g), each grade into 100 minutes, and each minute into 100 seconds. Though less common, it offers computational simplicity in certain engineering contexts.

Circular System (Radian Measure): The most mathematically natural system defines one radian as the angle subtended at a circle's center by an arc equal in length to the radius. The relationship θ = s/r (where θ is the angle in radians, s is arc length, and r is radius) makes radians indispensable in calculus and advanced mathematics.

The three systems relate through the fundamental relationship: D/90 = G/100 = 2R/π, where D represents degrees, G represents grades, and R represents radians.

The Six Trigonometric Ratios

For a right-angled triangle with angle θ, the six trigonometric ratios are defined relative to the angle's position:

• Sine (sin θ): perpendicular/hypotenuse
• Cosine (cos θ): base/hypotenuse
• Tangent (tan θ): perpendicular/base
• Cosecant (cosec θ): hypotenuse/perpendicular (reciprocal of sine)
• Secant (sec θ): hypotenuse/base (reciprocal of cosine)
• Cotangent (cot θ): base/perpendicular (reciprocal of tangent)

These ratios remain constant for a given angle regardless of the triangle's size, making them powerful tools for solving problems involving unknown lengths or angles.

Fundamental Trigonometric Identities

Trigonometric identities are equations that hold true for all permissible values of the angle. Three categories of identities form the foundation:

Pythagorean Identities:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

Quotient Identities:

• tan θ = sin θ / cos θ
• cot θ = cos θ / sin θ

Reciprocal Identities:

• sin θ = 1/cosec θ
• cos θ = 1/sec θ
• tan θ = 1/cot θ

These identities are not merely mathematical curiosities—they enable simplification of complex expressions, prove other relationships, and solve equations that would otherwise be intractable.

Trigonometric Ratios of Standard Angles

Memorizing the values for 0°, 30°, 45°, 60°, and 90° is essential for efficient problem-solving. These can be derived geometrically:

• 45° ratios come from an isosceles right triangle where both legs are equal
• 30° and 60° ratios derive from an equilateral triangle bisected to create a 30-60-90 triangle
• 0° and 90° ratios represent limiting cases as the angle approaches these extremes

For instance, sin 45° = cos 45° = 1/√2, while sin 30° = 1/2 and sin 60° = √3/2. Understanding the geometric origins of these values provides deeper insight than rote memorization.

Complementary Angle Relationships

Two angles are complementary when their sum equals 90°. The complementary angle relationships are particularly elegant:

• sin(90° - θ) = cos θ
• cos(90° - θ) = sin θ
• tan(90° - θ) = cot θ
• cosec(90° - θ) = sec θ
• sec(90° - θ) = cosec θ
• cot(90° - θ) = tan θ

These relationships significantly simplify calculations and allow conversion between different trigonometric functions. For example, sin 25° = cos 65°, which can be useful when table values or calculator functions are limited.

Key Trigonometric Formulas Reference Table

Formula Name	Mathematical Expression	Explanation
Radian Definition	θ = s/r	Angle in radians equals arc length divided by radius
System Conversion	D/90 = G/100 = 2R/π	Converts between degrees, grades, and radians
Pythagorean Identity 1	sin²θ + cos²θ = 1	Fundamental relationship from Pythagoras' theorem
Pythagorean Identity 2	1 + tan²θ = sec²θ	Derived by dividing identity 1 by cos²θ
Pythagorean Identity 3	1 + cot²θ = cosec²θ	Derived by dividing identity 1 by sin²θ
Tangent Quotient	tan θ = sin θ / cos θ	Tangent as ratio of sine to cosine
Cotangent Quotient	cot θ = cos θ / sin θ	Cotangent as ratio of cosine to sine
Sine-Cosine Reciprocal	sin θ · cosec θ = 1	Product of function and cofunction equals 1
Complementary Sine	sin(90° - θ) = cos θ	Sine of complement equals cosine
Complementary Tangent	tan(90° - θ) = cot θ	Tangent of complement equals cotangent

Problem-Solving Strategies

Successful trigonometry problem-solving requires systematic approaches:

1. Identify the triangle configuration: Determine which angle is the reference angle and label perpendicular, base, and hypotenuse accordingly.
2. Apply the Pythagorean theorem: When two sides are known, calculate the third using a² + b² = c².
3. Use appropriate identities: Select identities that eliminate unknowns or simplify expressions.
4. Verify complementary relationships: Check if angles sum to 90° to exploit complementary angle formulas.
5. Rationalize denominators: Express answers in simplified radical form where appropriate.

Trigonnometry

The word trigonometry is originated from the greek word ‘tri’ means three, ‘gonia’ means angle and “metron” means measure. Hence the word trigonometry means three angle measure i.e. it is the study of geometrical figures which have three angles i.e. triangle.

Angle 

A measure formed between two rays having a common initial point is called an angle. The two rays are called the arms or sides of the angle and the common initial point is called the vertex of the angle.

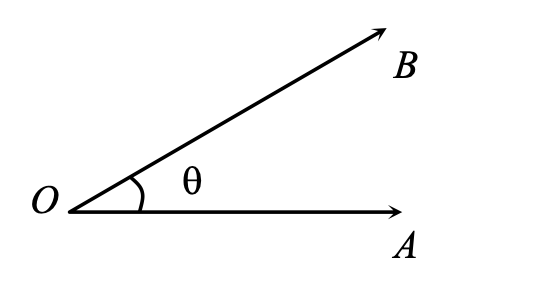
In the above figure OA is said to be ‘initial side’ and the other ray is said to be ‘terminal side’.

SYSTEMS OF MEASUREMENT OF ANGLES:

(i) Sexagesimal system: In this system a right angle is divided into 90 equal parts called degrees. Each degree is divided into 60 equal parts called minutes and each minute is divided into 60 equal parts called seconds.

Thus, 1 right angle = 90 degrees ( 90°)

1° = 60 minutes (60')

1’ = 60 seconds (60").

(ii) Centesimal system: In this system a right angle is divided into 100 equal parts, called grades. Each grade is sub divided into 100 minutes, and each minute into 100 seconds.

Thus, 1 right angle = 100 grades (100^g)

1 grade = 100 minutes (100')

1 minute =100 seconds (100").

(iii) Circular system: In this system the unit of measurement is radian. One radian, written as 1^o, is the measure of an angle subtended at the centre of a circle by an arc of length equal to the radius of the circle.

The number of radians in an angle subtended by an arc of a circle at the centre is equal length of arc/radius

TRIGONOMETRY FORMULAS

Arc Length Formula

∴ θ = s/r

Where θ = angle in radian, s = arc length and r = radius. Strikethrough

RELATION BETWEEN THREE SYSTEM OF MEASUREMENT OF ANGLES:

D/90 = G/100 = 2R/π

Where,

• D = number of degrees,
• G = number of grades,

and

• R = number of radians.

(i) The angle between two consecutive digits in a clock = 30^o( $\pi$/6 radians).

(ii) The hour hand rotates through an angle of 30^o in one hour, i.e. (1/2)^o in one minute.

(iii) The minute hand rotates through an angle of 6° in one minute.

1. Express 110° 30' in radians.

Sol. 110°30' = 110°(30/60)° = (110 + 1/2)° = (221/2) × (π^c/180) = (221π^c)/360

2. Express in degrees: (a) (2π/15)^c, (b) (−2)^c

Sol. (a) (2π/15)^c = (2π/15 × 180/π)° = 24°

(b) (−2)^c = (−2 × 180/π)° = (180/22 × 7 × (−2))° = (−114 + 6/11)°

= −114° (6/11 × 60)' = −114° (32 + 8/11)'

= −114° 32' (8/11 × 60)" = −114° 32' 44".

3. One angle of a triangle is (2x/3) grades another is (3x/2) degrees, whilst the third is (πx/375) radians; express them all in degrees.

Sol. (2/3)x^g = (2/3)x(9°/10) = (3/5)x° and (πx°/75) = (x/75)180° = (12x°/5)

But (3/5)x° + (3/2)x° + (12/5)x° = 180°

∴ 6x° + 15x° + 24x° = 1800° 45x° = 1800° x = 40°

Hence, three angles of the triangle are 24°, 60° and 96°.

4. The angles of a triangle are in A.P. and the number of degrees in the least is to the number of radians in the greatest as 60 to π^c. Find the angles in degrees.

Sol.The three angles in A.P.; if y is common difference, let these angles be (x + y)°, x° and (x - y)°

∴ x + y + x + x - y = 180°

∴ x = 60°

According to the question, (x−y)/(x+y)π^c/180 = 60/π

or π(x−y)=(x+y)π/180×60

or 3(x - y) = x + y

or 4y = 2x

or y = x/2

∴ y=60°/2=30°

Hence three angles are 30°, 60° and 90°.

TRIGONOMETRIC

A right angled triangle is shown in Figure. ∠B is of 90° Side opposite to ∠B is called hypotenuse. There are two other angles i.e. ∠A and ∠C. If we consider ∠C as θ, then side opposite to this angle is called perpendicular and side adjacent to θ is called base.

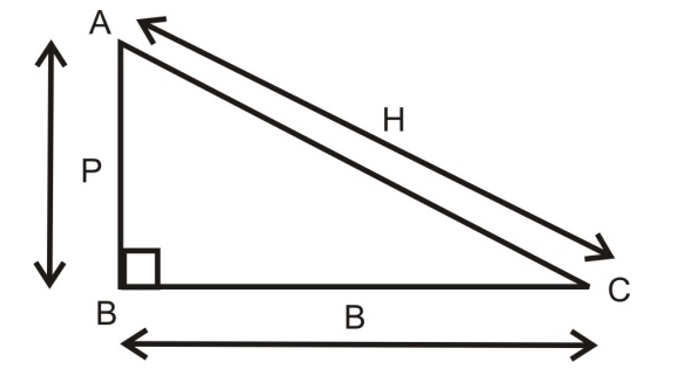
In the diagram:

• The triangle ABC has a right angle at B (indicated by the small square)
• Side AB is labeled as P (perpendicular)
• Side BC is labeled as B (base)
• Side AC is labeled as H (hypotenuse)
• Arrows indicate the direction/orientation of each side

THE SIX TRIGONOMETRY RATIO ARE:

sin θ = Perpenicular/Hypotenuse = P/H = AB/AC

cosec θ = Hypotenuse/Perpendicular = H/P = AC/AB

cos θ = Base/Hypotenuse = B/H = BC/AC

sec θ = Hypotenuse/Base = H/B = AC/BC

tan θ = Perpendicular/Base = P/B = AB/BC

cot θ = Base/Parpendicular = B/P = BC/AB

INTERRELATIONSHIP BETWEEN THE BASIC TRIGONOMETRIC RATIO:

tan θ = 1/cot θ ⇒ cot θ = 1/tan θ

cos θ = 1/sec θ ⇒ sec θ = 1/cos θ

sin θ = 1/cosec θ ⇒ cosec θ = 1/sin θ

We also observe that

tan θ = sin θ/cos θ ⇒ cot θ = cos θ/sin θ

TRIGONOMETRIC RATIOS OF SOME SPECIFIC ANGLES

TRIGONOMETRIC RATIOS OF 45°:

Let △ABC be a right-angled triangle in which ∠B = 90° and ∠A = 45°.

Then, ∠C = 45° [Angle sum property]

∠A = ∠C ⇒ AB = BC. [Side opposite to equal angles]

Let AB = BC = x units. Then,

AC = √(AB² + BC²) = √(x² + x²) = √(2x²) = √(2x) units.

∴ base = AB = x units;

perpendicular = BC = x units and

hypotenuse = AC = √(2x) units.

∴ sin 45° = BC/AC = x/√(2x) = 1/√2;

cos 45° = AB/AC = x/√(2x) = 1/√2;

tan 45° = BC/AB = x/x = 1; cosec 45° = 1/sin 45° = √2;

sec 45° = 1/cos 45° = √2; cot 45° = 1/tan 45° = 1.

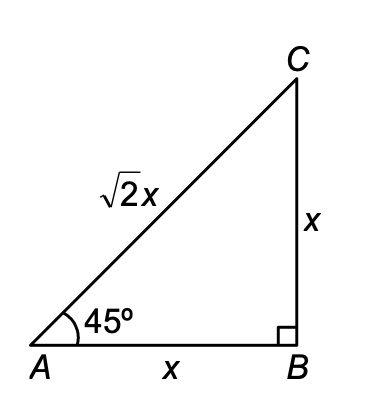
[DIAGRAM: Right triangle ABC with right angle at B, angle of 45° at A, sides labeled as: AB = x (base), BC = x (perpendicular height), AC = √(2x) (hypotenuse), and angle C = 45°]

TRIGONOMETRIC RATIOS OF 60° AND 30°:

Consider an equilateral △ABC with each side equal to 2x.

Then, each angle of △ABC is 60°.

From A, draw AD ⊥ BC.

Then, clearly, BD = DC = x.

Also, ∠ADB = 90°.

∴ ∠BAD = 30°. [Angle sum property]

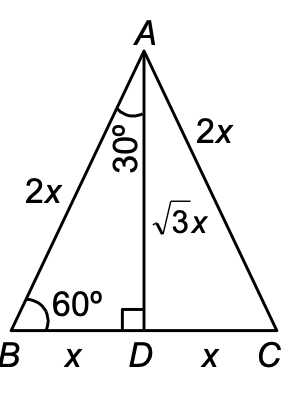
From right-angled △ADB, we have:

AD = √(AB² - BD²) = √((2x)² - x²) = √(4x² - x²) = √(3x²) = √3x

[Diagram shows triangle with side 2x, angle 60° at B, and base segment x]

T-RATIOS OF 60°:

In right-angled △ADB, we have

base = BD = x; perpendicular = AD = √3x and hypotenuse = AB = 2x

∴ sin 60° = AD/AB = (√3x)/(2x) = √3/2; cos 60° = BD/AB = x/(2x) = 1/2;

tan 60° = AD/BD = (√3x)/x = √3; cosec 60° = 1/(sin 60°) = 2/√3;
sec 60° = 1/(cos 60°) = 2; cot 60° = 1/(tan 60°) = 1/√3.

T-RATIOS OF 30°:

In right-angled ΔADB, we have

base = AD = √3x, perpendicular = BD = x and hypotenuse = AB = 2x.

∴ sin 30° = BD/AB = x/2x = 1/2; cos 30° = AD/AB = √3x/2x = √3/2;

tan 30° = BD/AD = x/√3x = 1/√3; cosec 30° = 1/sin 30° = 2;

sec 30° = 1/cos 30° = 2/√3; cot 30° = 1/tan 30° = √3;

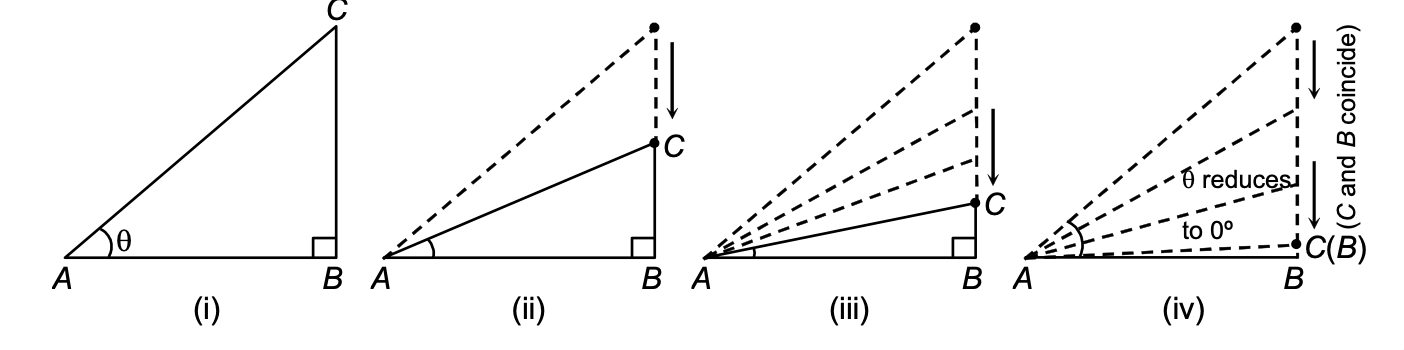
TRIGONOMETRIC RATIOS OF 0º:

 

Here is the text conversion with all mathematical symbols and expressions:

In the figure (i), ΔABC is right angled at B and ∠BAC = θ.

In figure (ii), ∠BAC is reduced and it is less than θ. Here, we observe that the point C moves closer to the point B.

In figure (iii), ∠BAC is very small and the point C is also very close to the point B.

In figure (iv), ∠BAC just reduces to 0° and the point C coincides with the point B, i.e., BC = 0 and AB = AC. Then by definition, the values of the trigonometric ratios of 0° are as under:

sin 0° = BC/AC = 0/AC = 0

cos 0° = AB/AC = AC/AC = 1

tan 0° = sin 0°/cos 0° = 0/1 = 0

cosec 0° = 1/sin 0° = 1/0

sec 0° = 1/cos 0° = 1/1 = 1

cot 0° = 1/tan 0° = 1/0

Hence, we have

sin 0° = 0,cos 0° = 1,tan 0° = 0,sec 0° = 1.

The values of cosec 0° and cot 0° are not defined as real numbers.

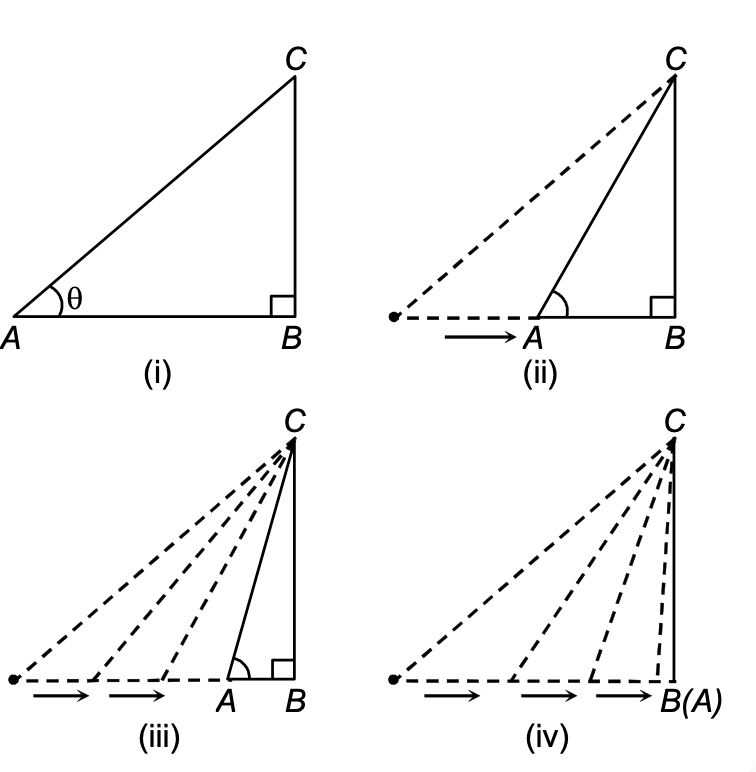
TRIGONOMETRIC RATIOS OF 90°:

We observe from the figures (i, ii, iii, iv) that as the point A moves closer to the point B, the angle ∠BAC becomes larger and larger and ultimately when A coincides with B, the angle ∠BAC becomes equal to 90°.

Thus, when ∠BAC = 90°, we have AB = 0, BC = AC because AC and BC coincide.

Now, we get

sin 90° = BC/AC = AC/AC = 1

cos 90° = AB/AC = 0/AC = 0

tan 90° = sin 90°/cos 90° = 1/0

Here's the text conversion of the image with all mathematical symbols and expressions:

cosec 90° = 1/sin 90° = 1/1 = 1 ⇒ sec 90° = 1/cos 90° = 1/0 ⇒ cot 90° = cos 90°/sin 90° = 0/1 = 0.

Hence, we have the values of the trigonometric ratios of 90° as under:

sin 90° = 1, cos 90° = 0, cosec 90° = 1, cot 90° = 0.

The values of sec 90° and tan 90° are not defined as real numbers.

➜ The value of sin θ increases from 0 to 1 as the angle θ increases from 0° to 90°.

➜ The value of cos θ decreases from 1 to 0 as the angle θ increases from 0° to 90°.

TRIGONOMETRIC TABLE

θ →	0	30°	45°	60°	90°
Sin	0	1/2	1/√2	√3/2	1
Cos	1	√3/2	1/√2	1/2	0
Tan	0	1/√3	1	√3	Not defined
Cot	Not defined	√3	1	1/√3	0
Sec	1	2/√3	√2	2	Not defined
Cosec	Not defined	2	√2	2/√3	1

 

TRIGONOMETRIC IDENTITIES

(i) sin²θ + cos²θ = 1

• (A) sin²θ = 1 − cos²θ
• (B) cos²θ = 1 − sin2θ

(ii) 1 + tan²θ = sec²θ

• (A) sec²θ − 1 = tan²θ
• (B) sec²θ − tan²θ = 1
• (C) tan²θ − sec²θ = −1

(iii) 1 + cot²θ = cosec²θ

• (A) cosec²θ − 1 = cot²θ
• (B) cosec²θ − cot²θ = 1
• (C) cot²θ − cosec²θ = −1

QUOTIENT RELATION OF T-RATIOS

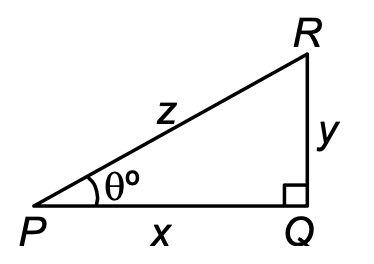
THEOREM 1:

For any acute angle θ, prove that

(i) tan θ = sin θ / cos θ;
(ii) cot θ = cos θ / sin θ.

Proof: Consider a right-angled ΔPQR in which ∠Q = 90° and ∠P = θ°. Let PQ = x units, RQ = y units and PR = z units. Then,

[Right triangle diagram showing angle θ° at P, with sides labeled: x along PQ, y vertical at Q, and z as hypotenuse PR]

(i) tan θ = y/x = (y/z)/(x/z) [dividing num. and denom. by z]

= sin θ / cos θ.

∴ tan θ = sin θ / cos θ.

(ii) cot θ = x/y = (x/z)/(y/z) [dividing num. and denom. by z] = cos θ / sin θ.

SQUARE RELATION

THEOREM 2:

For any acute angle θ, prove that

(i) sin²θ + cos²θ = 1;

(ii) 1 + tan²θ = sec²θ;

(iii) 1 + cot²θ = cosec²θ.

Proof: Consider a right-angle △PQR in which ∠Q = 90° and ∠P = θ°. Let PQ = x units, RQ = y units and PR = z units.

Then, by Pythagoras' theorem, we have

x² + y² = z²

Now, (i) sin²θ + cos²θ = (y/z)² + (x/z)² = (y²/z² + x²/z²) = (x² + y²)/z² = z²/z² = 1.

[∵ x² + y² = z²]

∴ sin²θ + cos²θ = 1.

(ii) 1 + tan²θ = 1 + (y/x)² = 1 + y²/x² = (y² + x²)/x² = z²/x² [∵ x² + y² = z²]

= (z/x)² = sec²θ.

∴ 1 + tan²θ = sec²θ.

(iii) 1 + cot²θ = 1 + (x/y)² = 1 + x²/y² = (x² + y²)/y² = z²/y² [∵ x² + y² = z²]

= (z/y)² = cosec²θ.

∴ 1 + cot²θ = cosec²θ.

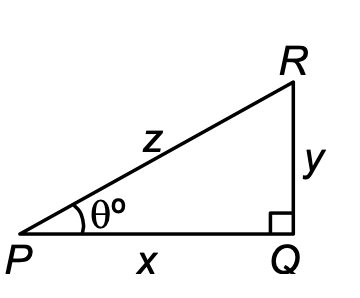
Diagram description: There is a right triangle PQR with:

• Right angle at Q (marked with a small square)
• Angle θ° at P
• Horizontal side PQ labeled as x
• Vertical side QR labeled as y
• Hypotenuse PR labeled as z
• Point R at top right, P at bottom left, Q at bottom right

Ex. If tan θ = m/n, then find sin θ.

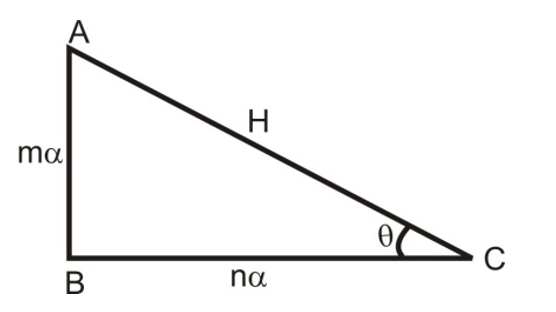
Solution:

Let P = mα and B = nα

[There is a right-angled triangle ABC where:

• Point A is at the top
• Point B is at the bottom left (right angle)
• Point C is at the bottom right
• The vertical side AB has length mα
• The horizontal side BC has length nα
• The hypotenuse AC is labeled H
• The angle at C is labeled θ]

∴ tan θ = P/B = m/n

H² = P² + B²

H² = m²α² + n²α²

H = α√(m² + n²)

∴ tan θ = P/H = mα/(α√(m² + n²))

sin θ = m/√(m² + n²)

Ex.: Given that cos (A − B) = cos A cos B + sin A sin B, find the value of cos 15°.

Sol. Putting A = 45° and B = 30°, we get

we get cos (45° − 30°) = cos 45° cos 30° + sin 45° sin 30°

⇒ cos 15° = (1/√2) × (√3/2) + (1/√2) × (1/2) ⇒ cos 15° = (√3 + 1)/(2√2)

Trigonometric Ratios of Coplementry Angles 

Let us construct a right-angled △ABC in which ∠ABC = θ, ∠BCA = 90°.

Then we have ∠BAC = (90° - θ). Angles θ and (90° - θ) are defined as complementary angles.

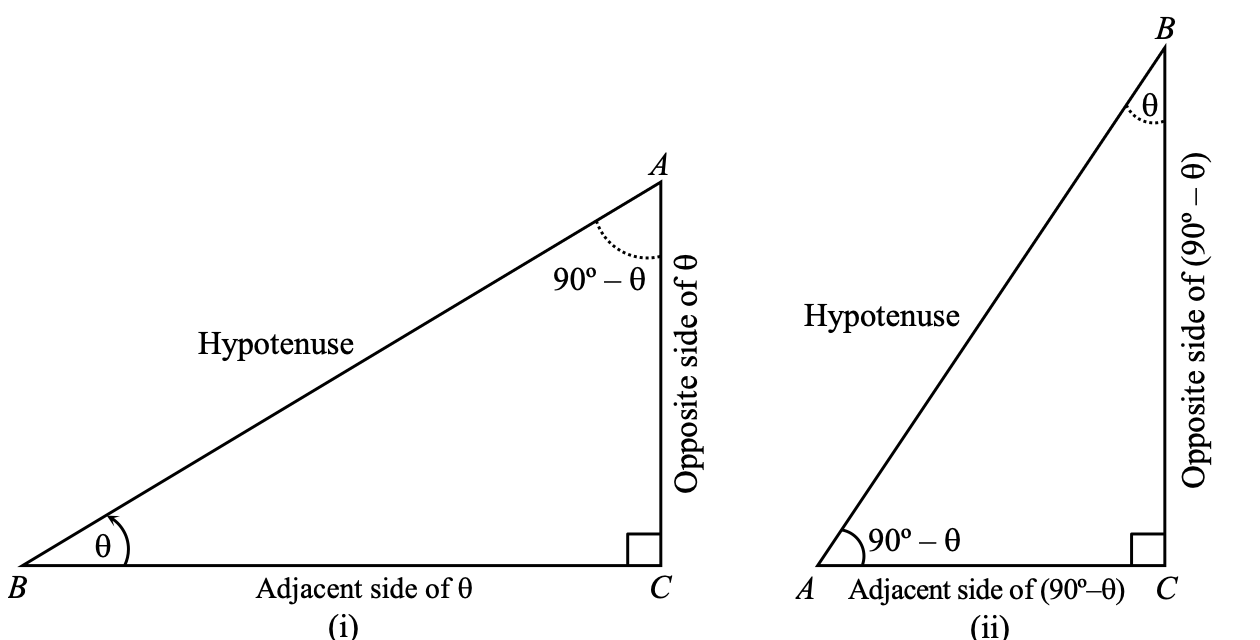
[Two right triangles are shown side by side]

Figure (i):

• Right-angled triangle with vertices B, A, C
• Angle θ at vertex B
• Angle (90° - θ) at vertex A
• Right angle (90°) at vertex C
• Hypotenuse: BA
• Opposite side of θ: AC (vertical side)
• Adjacent side of θ: BC (horizontal base)

Figure (ii):

• Right-angled triangle with vertices A, B, C
• Angle (90° - θ) at vertex A
• Angle θ at vertex B
• Right angle (90°) at vertex C
• Hypotenuse: AB
• Opposite side of (90° - θ): BC (vertical side)
• Adjacent side of (90° - θ): AC (horizontal base)

In figure (i), the sides are labelled corresponding to angle θ and in fig

Here is the text conversion with all mathematical symbols and expressions:

From figure (ii), we have sin (90° - θ) = BC/BA and from figure (i), we have BC/BA = cos θ.

∴ sin (90° - θ) = BC/BA = cos θ.

Similarly, cos (90° - θ) = AC/BA = sin θ

tan (90° - θ) = BC/AC = cot θ

cosec (90° - θ) = BA/BC = sec θ

sec (90° - θ) = BA/AC = cosec θ

cot (90° - θ) = AC/BC = tan θ.

If A and B are two complementary acute angles, i.e., A + B = 90°, then we have

sin A = sin (90° - B) = cos B

cos A = cos (90° - B) = sin B

tan A = tan (90° - B) = cot B

cosec A = cosec (90° - B) = sec B

sec A = sec (90° - B) = cosec B

cot A = cot (90° - B) = tan B.

ure (ii), the sides are labelled corresponding to angle (90° - θ).

Ex.: If tan A = 3/4 and A + B = 90°, then what is the value of cot B?

Sol. A + B = 90° [Given]

⟹ B = 90° - A ⟹ cot B = cot (90° - A)

⟹ cot B = tan A = 3/4.

Ex.: If cosec A = √10 and A + B = 90°, then what is the value of sec B?

Sol. sec B = sec (90° - A) [∵ A + B = 90° ⟹ B = 90° - A]

= cosec A = √10.

Trigonometry forms a cornerstone of mathematical education, bridging geometry and algebra while providing practical tools for science and engineering. Mastery requires understanding the geometric foundations of the ratios, memorizing standard values, and practicing application of identities. The relationships between complementary angles and the Pythagorean identities unlock most problems encountered at intermediate levels. With systematic practice and conceptual understanding, trigonometry transitions from abstract formulas to an intuitive language for describing relationships in space.