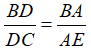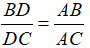About Angle Bisector Theorem
The opposite side of a triangle is divided into two segments proportional to the triangle's other two sides, according to the angle bisector theorem.
The opposite side of a triangle is divided into two segments proportional to the triangle's other two sides, according to the angle bisector theorem. A ray that divides a given angle into two equal angles is referred to as an angle bisector.
What is Angle Bisector Theorem?
According to the triangle angle bisector theorem, the angle bisector of every angle splits opposite sides in the ratio of sides containing the angle.
An angle bisector is a line or ray that divides an angle in a triangle into two equal measures. The angle bisector's key qualities are that every point on its bisector is equidistant from the angle's sides, and the angle bisector divides the opposing side of a triangle in the ratio of the neighbouring sides, which is known as the angle bisector property of triangle.
Angle Bisector Theorem Proof
The angle bisector of any angle in a triangle divides the opposing side in the ratio of the sides containing the angle.
Given: ?ABC in which AD is the internal bisector of ∠A.
To Prove :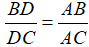
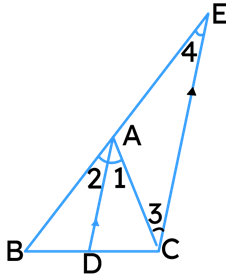
Construction: Draw CE&DA, meeting BA produced at E. Proof :
∠1 = ∠2 ………(1) AD is the bisector of ∠A
∠2 = ∠3 ……..(2) Alt. ∠s are equal, as CE||DA and AC is the transversal
∠1 = ∠4 ………(3) Corres. ∠s are equal, as CE||DA and BE is the transversal
∠3 = ∠4 From 1, 2 and 3.
AE = AC ……..(4) Sides opposite to equal angles are equal
In ? BCE, DA||CE
Find pdf of the solved example of Angle Bisector Theorem
