About Average Deviation Formula
To characterise the dispersion among a group of data, the average deviation formula is utilised. The average deviation is the difference between each observation's mean value and its average deviation. Before calculating the average deviation, the mean of the data is computed. An average deviation formula is a useful tool for quickly calculating the average deviation and arriving at a result. Let's look at the average deviation formula with examples.
What Is the Average Deviation Formula?
The average deviation formula is used to determine the average deviation of an observation based on its mean value. The following is the average deviation formula for n number of observations:
Average Deviation = 1/n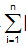
xi - x? |
Where
xi = Data values in the given set.
x? is mean.
n is the total number of data values
Average Deviation Formula Examples
Example 1: Using the average deviation formula, calculate the average deviation of the given data: 12, 14, 16, 18, 20, 22.
Sol: average deviation
Given: n = 6
x? = (12 +14 + 16 + 18 + 20 + 22)/6 = 17
By using the average deviation formula
Average deviation = (|12 - 17| + |14 - 17| + |16 - 17| + |18 - 17| + |20 - 17| + |22 - 17|)/6
= (5 + 3 + 1 + 1 + 3 + 5)/6 = 18/6 = 3
Average deviation = 3
Example 2: Using the average deviation formula, find the average deviation of the given data: 33, 44, 55, 66, 77, 88, 99.
Sol: average deviation
Given: n = 7
Grinding mean of the given data:
x? = (33 + 44 + 55 + 66 + 77 + 88 + 99)/7 = 66
By using the average deviation formula,
Average deviation = (|33 - 66| + |44 - 66| + |55 - 66| + |66 - 66| + |77 - 66| + |88 - 66| + |99 - 66|)/7
Average deviation = 18.857
To get all the Maths formulas to check out the main page.
Find the pdf of the Average Deviation Formula
Frequently Asked Questions
The Average Deviation Formula is used to measure the dispersion of data points from the central value (mean or median). It is given by:
Average Deviation=∑∣xi−M/n
where xi represents each data point, M is the mean or median, and n is the total number of values. This formula helps in understanding data variability in statistics.
The Average Deviation Formula measures the mean of absolute deviations from the central value, whereas Standard Deviation considers squared deviations and then takes the square root. Unlike standard deviation, average deviation is simpler but less commonly used because it does not emphasize larger deviations as strongly.