Binomial Expansion

About Binomial Expansion

The binomial expansion, commonly known as the binomial theorem, is a formula for expanding the exponential power of a binomial expansion.

The following is the binomial expansion of (x + y)n using the binomial theorem:,

(x + y)n = nC0xny0+nC1xn-1y1+.......+nCn-1x1yn - 1+nCnx0yn

Binomial Theorem Formula

In order to expand any binomial power into a series, the binomial theorem formula is needed. The formula for the binomial theorem is (a+b)n = Binomial Expansion nCr an-rbr, where n is a positive integer and a, b are real numbers, and 0 < r ≤ n. This formula can be used to expand binomial expressions like (x + a)10, (2x + 5)3, (x - (1/x))4, and so on. The formula for the binomial theorem aids in the expansion of a binomial raised to a particular power. If x and y are both real numbers, then the binomial theorem holds for all n ∈ N,

(x + y)n = nc0xny0 + nc1xn-1y1 + nc2xn-2y2-------+ncn-1x1yn-1 + ncnx0y0

⇒ (x + y)n = 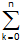Binomial Expansion2nCk xn - ky k

where, nCr = n! / [r! (n - r)!]

Binomial Theorem Expansion Proof

Let x, a, n ∈ N. Let us use the idea of mathematical induction to show the binomial theorem formula. It is sufficient to demonstrate for n = 1, n = 2, and n = 3, for n = k ≥ 2, and for n = k+ 1.

obviously (x +y)1 = x +y and (x +y)2 = (x + y) (x +y) = x2 + xy + xy + y2 = x2 + 2xy + y2

As a result, the result holds for both n = 1 and n = 2. Make k a positive number. Let’s prove that the result is true for k ≥ 2.

  1. By assuming (x + y)n = 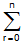Binomial Expansion1 nCr xn-ryr
  2. (x + y)k = kCrxn-ryr
  3. (x+y)k = kC0 xky0 +kC1xk-1y1 + kC2xk-2y2+ ... + kCrxk-ryr +....+ kCkxk-kyk

Hence, this result is true for n = k ≥ 2.

Now by considering the expansion also for n = k + 1.

  1. (x + y) k+1 = (x + y) (x + y)k
  2. =(x + y) (xk + kC1 xk-1y1 + kC2 xk-2y2+ ... + kCr xk-ryr +....+ yk)
  3. = xk+1 + k+1C1xky + k+1C2xk-1y2 + ... + k+1Crxk-ryr + …... + k+1Ckxyk + yk+1 [Because nCr + nCr-1 = n+1Cr]

Thus the result is true for n = k+1. By mathematical induction, this result is true for all positive integers 'n'. Hence proved.To get all the Maths formulas check out the main page. 

Find pdf of Binomial Expansion proof of the formula

Binomial Expansion

Related Links

Frequently Asked Questions on Binomial Expansion