Calculus Formulas

About Calculus Formulas

Here are some basic calculus formulas for some common functions' derivatives and integrals. The derivative with respect to x is denoted by d/dx, and the integral of a function, f, with respect to x is denoted by f(x)dx. Furthermore, because all of the integrals are indefinite, they all have a +C constant term. Because a constant's derivative is zero, the anti-derivative of a function might include constant terms.

Derivative Rules

  1. Exponential/Logarithmic Functions:
    1. d(ex)/dx=ex
    2. d(ax)/dx=ax⋅ln(a)
    3. d(ln(x))/dx=1/x
    4. d(logax)/dx=1/xln(a)
  2. Trigonometric Functions:
    1. d(sin(x))/dx=cos(x)
    2. d(cos(x))/dx=−sin(x)
    3. d(tan(x))/dx=sec2(x)
    4. d(cosec(x))/dx=−cosec(x)cot(x)
    5. d(sec(x))/dx=sec(x)tan(x)
    6. d(cot(x))/dx=−cosec2(x)
  3. Inverse Trigonometric Functions:
    1. d(sin−1(x))/dx=1/(1−x2)
    2. d(cos−1(x))/dx=−1/(1−x2)
    3. d(tan-1x)/dx=1/(1+x2)
    4. d(csc-1x)/dx=−1/x √(x2−1)
    5. d(sec-1x)/dx=1/x√(x2−1)
    6. d(cot-1x)/dx=−1/(1+x2)
  4. These are just a few of the derivative rules for common functions that arise in differential calculus.
    1. Integral Rules
    2. ∫(1/x)dx=ln|x|+C
    3. ∫exdx=ex+C
    4. ∫axdx=axln(a)+C
    5. ∫sin(x)dx=−cos(x)+C
    6. ∫cos(x)dx=sin(x)+C
    7. ∫tan(x)dx=ln|sec(x)|+C
    8. ∫cot(x)dx=ln|sin(x)|+C
    9. ∫sec(x)dx=ln|sec(x)+tan(x)|+C
    10. ∫csc(x)dx=ln|csc(x)−cot(x)|+C

These are just a few of the many different integral rules for disparate functions that may arise in integral calculus.

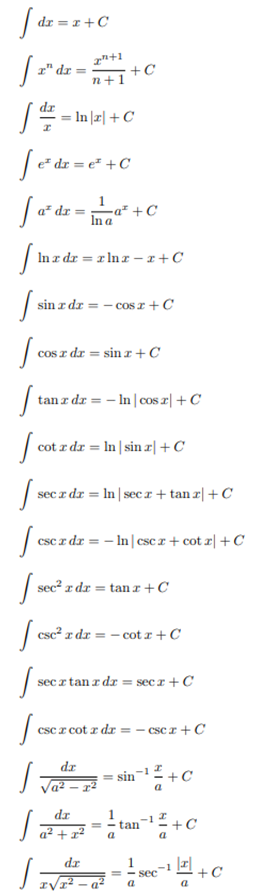
calculas formula1

To get all the Maths formulas check out the main page. 

Pdf of Calculus Formulas  Functions  And derivative  Rules

Calculus Formulas
Calculus Formulas

Related Links

Frequently Asked Questions on Calculus Formulas