About Euler's Formula
Leonhard Euler, a Swiss mathematician, devised Euler's formula. Euler's formulas are divided into two categories:
- It is a crucial formula for solving complex exponential functions in complex analysis. Euler's identity is another name for Euler's formula. It's used to show how trigonometric functions and complex exponential functions are related.
- For polyhedra, the number of faces, vertices, and edges is connected in a certain way, which is provided by Euler's formula, often known as Euler's characteristic, for any polyhedron that does not self-intersect.
2 different Euler's formulas are used in different contexts.
- Euler's formula - complex analysis: eix = cos x + isin x
- Euler's formula - polyhedra: faces + vertices - edges = 2
Euler's Formula For complex analysis
The Euler form of a complex number is significant enough to warrant its section. It's a really useful form that simplifies a lot of calculations. In complex analysis, Euler's formula is used to determine the relationship between trigonometric functions and complex exponential functions. Euler's formula can be written as follows for any real number x:
eix = cos x + isin x
The trigonometric functions cos and sin are used, as well as the imaginary unit I and the natural logarithm base e. This formula can be interpreted as a unit complex function eiθ tracing a unit circle in the complex plane, where θ is a real integer and is measured in radians. This illustration may appear perplexing at first. Raising a real number to an imaginary number makes no sense. You can rest assured, though, that there is a valid rationale for this relationship. Although we will not examine a rigorous proof for this, you can see why it should be true by looking at the following approximate proof. Do check out more Maths Formulas.
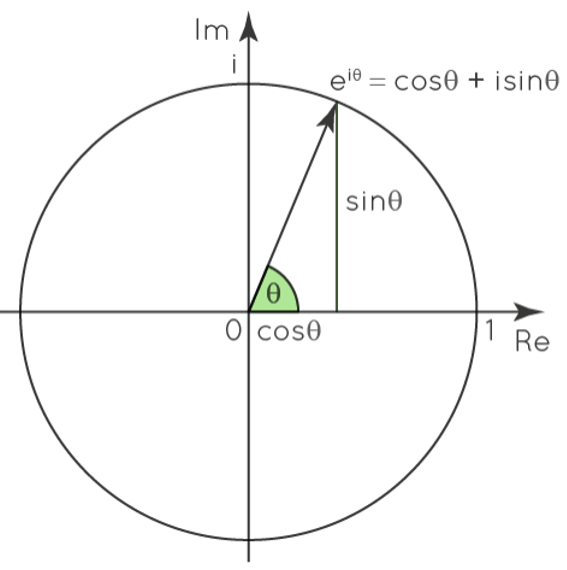
Euler's Identity
eix = cos x + isin x. x is replaced with π. Then we get
eiπ = cos π + isin π
eiπ = -1 + i (0) (as cos π = -1 and sin π = 0)
eiπ + 1 = 0
This is called as Euler's identity.
Euler's Formula For polyhedra
Polyhedra are three-dimensional solid objects with flat surfaces and straight edges. Cube, cuboid, prism, and pyramid are examples. The number of faces, vertices, and edges of every polyhedron that does not self-intersect is connected in a certain way. The number of vertices and faces together is exactly two greater than the number of edges, according to Euler's formula for polyhedra. The formula for a polyhedron given by Euler is:
F + V - E = 2
Here,
- F - number of faces,
- V - number of vertices, and
- E - number of edges.
Euler's Formula Use
The more generic formula is F + V - E = X, where X is the Euler characteristic. We demonstrate that Euler's formula can be used in any three-dimensional space, not just polyhedra. According to Euler's graph theory, there are exactly 5 regular polyhedra. We can check for a basic polyhedron with 10 faces and 17 vertices using Euler's formula calculator. Although the prism has 10 faces and an octagon as its basis, it has 16 vertices.
The Validation of Euler's Solid Formula
Solid shapes and complicated polyhedra are instances of Euler's formulas. Let's check the formula for a couple of simple polyhedra, like a square pyramid & a triangular prism.
- A square pyramid has 5 faces, 5 vertices, & 8 edges.
F + V − E = 5 + 5 − 8 = 2 - A triangular prism with 5 faces, 6 vertices, and 9 edges.
F + V − E = 5 + 6 − 9 = 2
Euler's Formula Explanation
Euler's formula can be demonstrated for five platonic solids. Cube, tetrahedron, octahedron, dodecahedron, and icosahedron are their names. Let's test Euler's formula on these complex polyhedra that serve as instances of Euler's formula.
| SOLID | F | v | E | Euler's Formula: F + V - E |
| Tetrahedron | 4 | 4 | 6 | 2 |
| Cube | 6 | 8 | 12 | 2 |
| Octahedron | 8 | 6 | 12 | 2 |
| Dodecahedron | 12 | 20 | 30 | 2 |