Cuboid
In the world of mathematics, we can observe various figures that are similar to the cuboid, such as the rectangular cuboid, rectangular box, right rectangular prism, right cuboid, rectangular parallelepiped, and rectangular hexagon. Let's dive deeper into the topic of cuboids and explore them in detail with examples.
Introduction to Cuboids
A cuboid is a three-dimensional geometric shape, also known as a solid shape. It is a convex polyhedron, meaning it is bounded by six rectangular faces, with eight vertices and twelve sides. A cuboid is a type of rectangular prism, and a solid with six square faces is called a cube.
Real-Life Examples of Cuboids
A common real-life example of a cuboid is a rectangular box, such as a shoebox or a cereal box. These everyday objects have the characteristic rectangular faces and edges that define a cuboid.
Related Geometric Shapes
While a cuboid is a specific type of three-dimensional shape, there are other similar figures that share some of its properties:
- Rectangular Cuboid: A cuboid with all rectangular faces.
- Rectangular Box: Another term used to describe a rectangular cuboid.
- Right Rectangular Prism: A cuboid with all right angles (90 degrees) between its faces.
- Right Cuboid: A cuboid with all right angles between its faces.
- Rectangular Parallelepiped: A three-dimensional shape with six rectangular faces, but the angles between the faces may not be right angles.
- Rectangular Hexagon: A two-dimensional shape with six rectangular sides.
Definition of cuboid
A cuboid is a three - dimensional solid with 6 faces (rectangular), 8 vertices and 12 edges. The three dimensions of a cuboid are length , width and height. A perfect cuboid is called a cuboid of integer edges.
If we consider Euler's formula, the relation between the faces (F), vertices (V) and edges (E) of a cuboid satisfies the equation:
F+V=E+2
6+8=12+2
12=12
Cuboid Shape
A cuboid is a closed 3D figure bounded by rectangular faces, which means the plane regions of the rectangle. The shape of a cuboid is shown in the figure below
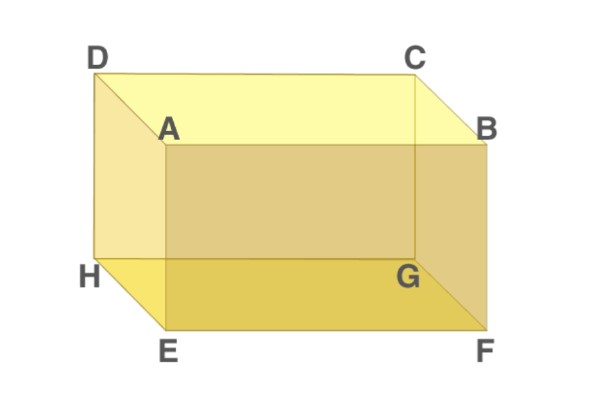
Faces,Edges and Vertices of Cuboid
A cuboid has 6faces, 8vertices and 12edges. All of these can be shown using the following notation:
Faces Cuboid
A cuboid is made up of six rectangular face. In the above diagram, there are six faces:
- ABFE
- DAEH
- DCGH
- CBFG
- ABCD
- EFGH
The pair of opposite and parallel face of the given cuboid are:
ABCD and EFGH(top and bottom faces respectively)
ABFE,DCGH and DAEH,CBFG (opposite and parallel face which are adjacent to the top and bottom face of the cuboid)
For each face, we can write the remaining face as their adjacent face such as the face ABCD is the adjacent to ABFE,BCGF,CDHG and ADHE.
Edges of Cuboid
The sides of all the rectangular faces are known as the sides of the cuboid. As we know that a cube has 12 edges. They are as follows : AB, AD, AE, HD, HE, HG, GF, GC, FE, FB, EF and CD Also, opposite side of a rectangle are equal.
Therefore,
- AB=CD=GH=EF
- AE=DH=BF=CG
- EH=FG=AD=BC
Vertices of Cuboid
The intersection point of the 3 sides of a cuboid is called a vertex of a cuboid and a cuboid has 8 vertices.
In the given cubic figure , there are 8 vertices A, B, C, D, E, F, G and H.
Let's take a look at visualizing the faces, edges and vertices of a cuboid.
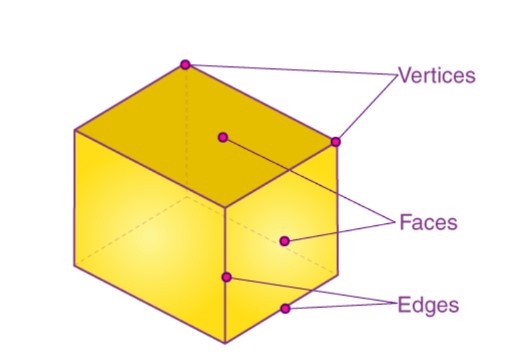
Properties of Cuboid
- A cuboid has 6 faces,12 edges and 8 vertices.
- All face of a cuboid are rectangular in shape
- opposite sides of a cuboid are parallel to each other
- A cuboid has three dimensions : length, width and height.
- All angles at the vertices of a cuboid are 90 degrees.
Surface Area of Cuboid
The surface area of any three-dimensional shape is the total area covered by all its faces. Similarly, the surface area of a cube is equal to the sum of the area of all its six rectangular face. The surface area of a cuboidal box can be divided into two types, namely lateral surface area and total surface area. Its formulas can be obtained from the figure below.
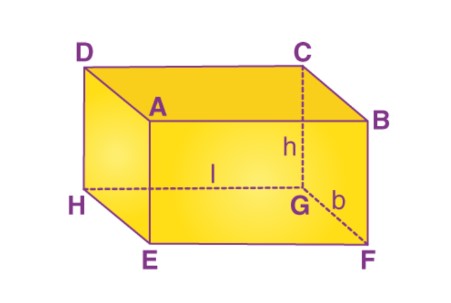
- AB=CD=GH=EF=l
- BC=AD=EH=FG=b
- CG=BF=AE=DH=h
Cuboid Lateral Surface Area
The lateral surface area (LSA) of a cuboid is the sum of the areas of all faces except the top and bottom faces.
Lateral surface area of the cuboid=Area of face ADHE+Area of face BCGF+Area of face ABFE+Area of DCGH
=ADDH+BCCG+ABBF+CDBC
=bh+bh+lh+lh
=2(bh)+2(lh)
=2h(l+b)
Lateral Surface Area (LSA) =2h(l+b) sq.units
Cuboid Total Surface Area
The total surface area (TSA) of a cuboid is the sum of the area of all its rectangular face.
Area of face EFGH=Area of face ABCD=lb
Area of face BFGC=Area of face AEHD=bh
Area of face DHGC=Area of face ABFE=lh
Total surface area of a cuboid = sum of the area of all its 6 rectangular face
=Area of(ABCD+EFGH+BFGC+AEHD+DHGC+ABFE)
=(lb)+(lb)+(bh)+(bh)+(lh)+(lh)
=2lb+2bh+2hl
=2(lb+bh+hl)
Total Surface Area (TSA) =2(lb+bh+hl)
Volume of Cuboid
The volume of a cube is equal to the product of the area of the base times its height. Thus, the volume of a cuboid is equal to the product of the rectangular face of the base and the height.
Volume=(LengthBreadth)Height
=(lb)h
=lbh
Volume=lbh cubic units
Diagonal of Cuboid
The lengths of the diagonals of a cuboid of dimensions l, b and h are given by the formula:
Diagonal=l2+b2+h2units
This formula is for the length of the space diagonal of a cuboid. Whereas the diagonals of a face of a cuboid are the diagonals joining the vertices on the faces of the cube. There are two diagonals for each face, so the total number of face diagonals that can be drawn in a cuboid is 12 (6 faces 2).
Perimeter of Cuboid
The perimeter of the cuboid will be the sum of the length of all the edges. Thus, from Figure above,
- AB=CD=GH=EF=length
- BC=AD=EH=FG=breadth
- CG=BF=AE=DH=height
Perimeter of cuboid
=AB+CD+EF+GH+BC+AD+EH+FG+CG+BF+AE+DH
=(l+l+l+l)+(b+b+b+b)+(h+h+h+h)
=4l+4b+4h
=4(l+b+h)
Perimeter (P) =4(l+b+h)units
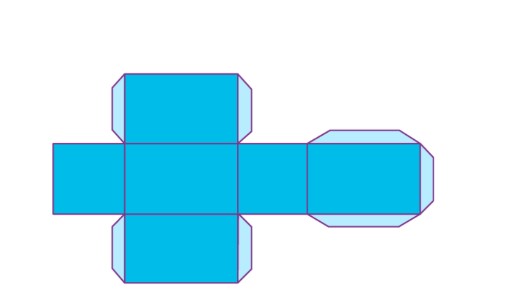
Cuboid Net
A solid shape mesh is a plane obtained by opening it in a line. This lattice will again become the original solid when we fold it. The number of different lattices for a solid or a rectangular cuboid of 3 different lengths is 54.
Example: Find the volume of a cuboid of length 10cm, breadth 8cm, height 4cm.
Solution :
length l=10cm
breadth b=8cm
height h=4cm
Volume=lbh
=1084
=320cm3
Related Links
- Derivative of Inverse Trigonometric functions
- Decimal Expansion Of Rational Numbers
- Cos 90 Degrees
- Factors of 48
- De Morgan’s First Law
- Counting Numbers
- Factors of 105
- Cuboid
- Cross Multiplication- Pair Of Linear Equations In Two Variables
- Factors of 100
- Factors and Multiples
- Derivatives Of A Function In Parametric Form
- Factorisation Of Algebraic Expression
- Cross Section
- Denominator
- Factoring Polynomials
- Degree of Polynomial
- Define Central Limit Theorem
- Factor Theorem
- Faces, Edges and Vertices
- Cube and Cuboid
- Dividing Fractions
- Divergence Theorem
- Divergence Theorem
- Difference Between Square and Rectangle
- Cos 0
- Factors of 8
- Factors of 72
- Convex polygon
- Factors of 6
- Factors of 63
- Factors of 54
- Converse of Pythagoras Theorem
- Conversion of Units
- Convert Decimal To Octal
- Value of Root 3
- XXXVII Roman Numerals
- Continuous Variable
- Different Forms Of The Equation Of Line
- Construction of Square
- Divergence Theorem
- Decimal Worksheets
- Cube Root 1 to 20
- Divergence Theorem
- Difference Between Simple Interest and Compound Interest
- Difference Between Relation And Function
- Cube Root Of 1728
- Decimal to Binary
- Cube Root of 216
- Difference Between Rows and Columns
- Decimal Number Comparison
- Data Management
- Factors of a Number
- Factors of 90
- Cos 360
- Factors of 96
- Distance between Two Lines
- Cube Root of 3
- Factors of 81
- Data Handling
- Convert Hexadecimal To Octal
- Factors of 68
- Factors of 49
- Factors of 45
- Continuity and Discontinuity
- Value of Pi
- Value of Pi
- Value of Pi
- Value of Pi
- 1 bigha in square feet
- Value of Pi
- Types of angles
- Total Surface Area of Hemisphere
- Total Surface Area of Cube
- Thevenin's Theorem
- 1 million in lakhs
- Volume of the Hemisphere
- Value of Sin 60
- Value of Sin 30 Degree
- Value of Sin 45 Degree
- Pythagorean Triplet
- Acute Angle
- Area Formula
- Probability Formula
- Even Numbers
- Complementary Angles
- Properties of Rectangle
- Properties of Triangle
- Co-prime numbers
- Prime Numbers from 1 to 100
- Odd Numbers
- How to Find the Percentage?
- HCF Full Form
- The Odd number from 1 to 100
- How to find HCF
- LCM and HCF
- Calculate the percentage of marks
- Factors of 15
- How Many Zeros in a Crore
- How Many Zeros are in 1 Million?
- 1 Billion is Equal to How Many Crores?
- Value of PI
- Composite Numbers
- 100 million in Crores
- Sin(2x) Formula
- The Value of cos 90°
- 1 million is equal to how many lakhs?
- Cos 60 Degrees
- 1 Million Means
- Rational Number
- a3-b3 Formula with Examples
- 1 Billion in Crores
- Rational Number
- 1 Cent to Square Feet
- Determinant of 4×4 Matrix
- Factor of 12
- Factors of 144
- Cumulative Frequency Distribution
- Factors of 150
- Determinant of a Matrix
- Factors of 17
- Bisector
- Difference Between Variance and Standard Deviation
- Factors of 20
- Cube Root of 4
- Factors of 215
- Cube Root of 64
- Cube Root of 64
- Cube Root of 64
- Factors of 23
- Cube root of 9261
- Cube root of 9261
- Determinants and Matrices
- Factors of 25
- Cube Root Table
- Factors of 28
- Factors of 4
- Factors of 32
- Differential Calculus and Approximation
- Difference between Area and Perimeter
- Difference between Area and Volume
- Cubes from 1 to 50
- Cubes from 1 to 50
- Curved Line
- Differential Equations
- Difference between Circle and Sphere
- Cylinder
- Difference between Cube and Cuboid
- Difference Between Constants And Variables
- Direct Proportion
- Data Handling Worksheets
- Factors of 415
- Direction Cosines and Direction Ratios Of A Line
- Discontinuity
- Difference Between Fraction and Rational Number
- Difference Between Line And Line Segment
- Discrete Mathematics
- Disjoint Set
- Difference Between Log and Ln
- Difference Between Mean, Median and Mode
- Difference Between Natural and whole Numbers
- Difference Between Qualitative and Quantitative Research
- Difference Between Parametric And Non-Parametric Tests
- Difference Between Permutation and Combination
Frequently Asked Questions on Cuboid
The main difference between a cube and a cuboid is their faces, that is, a cube has six square-shaped faces, while a cuboid has six rectangular faces. This mean that all edges of a cube are equal and that the edges of a cuboid can be written as group of 3 equal edges.
There is no difference between a cuboid and a rectangular prism as both will have 6 rectangular faces, 8 vertices and 12 edges. Plus, both look like a box.
A cuboid is a three-dimensional solid shape in geometry. A convex polyhedron bounded by six rectangular faces with eight vertices and twelve sides is called a cuboid. A cuboid is called a rectangular prism. A solid with a six square face is called a cube.
As we know that a cube is a special type of solid whose all the edges are equal in length. Therefore, A cuboid can have a square face.
All cuboids have height, length and breadth. They have six face, eight vertices and 12 edges. The sides of a cuboid are rectangular. All angle at the vertices are right angle.