Direct Proportion
Direct proportion describes a connection between two variables where their ratio remains constant. This constant is called the proportionality constant, often represented as "k". When variables x and y are directly proportional, their relationship can be expressed by the equation y = kx, where k is a constant that isn't zero.
What is Direct Proportion?
Direct proportion refers to a relationship between two variables where their ratio remains constant. This means as one variable increases or decreases, the other variable changes in a predictable way, keeping their ratio consistent. Mathematically, this relationship is expressed as y = kx, where y and x are the variables, and k is a constant called the constant of proportionality. This constant reflects how the variables are related, and it stays the same regardless of the values of x and y. Direct proportion is essential in various mathematical applications, such as calculating growth rates, time, distance, speed, and other real-world scenarios where relationships between quantities are linear and predictable.
Also Check: Differential Equations
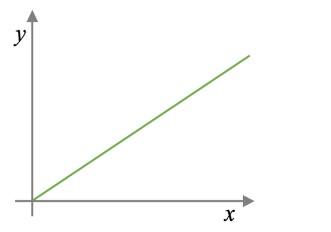
Direct Proportion Graphical fig:
Direct Proportion Examples in Real Life
Direct proportionality is a fundamental concept that describes how one quantity changes in relation to another. Here are some common examples where direct proportion can be observed:
-
Speed and Time: The distance traveled by a vehicle is directly proportional to its speed and the time it takes. If a vehicle's speed doubles, the time required to cover a certain distance is halved.
-
Height and Shadow Length: The height of an object and the length of its shadow follow a direct proportion. If you double the height of an object, its shadow length also doubles.
-
Volume and Gas Pressure: The volume of a gas is directly proportional to its pressure, provided the temperature remains constant. For instance, doubling the pressure of a gas results in its volume also doubling.
-
Current and Voltage in Circuits: In electrical circuits, the current flowing through a conductor is directly proportional to the voltage applied across it, assuming the resistance remains constant. If the voltage doubles, the current in the circuit also doubles.
-
Area and Side Length of a Square: The area of a square increases directly with the square of its side length. If you double the side length of a square, its area quadruples.
Also Check: Difference Between Variance and Standard Deviation
Direct Proportion Formula
The relationship in direct proportionality can be mathematically represented by the equation y = kx, where:
- y and x are the related quantities,
- k is the constant of proportionality.
To find the constant k, divide one known value of y by the corresponding value of x. This constant k remains consistent for any pair of y and x values that exhibit direct proportionality.
Practical Applications
Direct proportionality is useful in modeling various real-world scenarios involving growth, decay, time, distance, speed, and more. It provides a precise mathematical framework to understand and predict how quantities change relative to each other under specific conditions.
For instance, in physics and engineering, direct proportionality helps in designing systems where changes in one parameter affect another in a predictable manner. This includes designing circuits, understanding gas behavior under different pressures, and predicting the behavior of physical objects in varying conditions.
Also Check: Difference Between Variance and Standard Deviation
Graphical Representation of Direct Proportion
A direct proportionality graph is a straight line passing through the origin (0,0) with a slope equal to the constant of proportionality k. The x-axis represents one quantity (usually x), and the y-axis represents the other quantity (usually y). As x increases, y also increases in such a way that their ratio y/x remains constant, equal to k.
The equation of the straight line on the graph is y = kx, where the slope k represents how much y changes per unit change in x.
Direct Proportion Graph When you Double one you double the other:
.jpg)
Related Links
- Derivative of Inverse Trigonometric functions
- Decimal Expansion Of Rational Numbers
- Cos 90 Degrees
- Factors of 48
- De Morgan’s First Law
- Counting Numbers
- Factors of 105
- Cuboid
- Cross Multiplication- Pair Of Linear Equations In Two Variables
- Factors of 100
- Factors and Multiples
- Derivatives Of A Function In Parametric Form
- Factorisation Of Algebraic Expression
- Cross Section
- Denominator
- Factoring Polynomials
- Degree of Polynomial
- Define Central Limit Theorem
- Factor Theorem
- Faces, Edges and Vertices
- Cube and Cuboid
- Dividing Fractions
- Divergence Theorem
- Divergence Theorem
- Difference Between Square and Rectangle
- Cos 0
- Factors of 8
- Factors of 72
- Convex polygon
- Factors of 6
- Factors of 63
- Factors of 54
- Converse of Pythagoras Theorem
- Conversion of Units
- Convert Decimal To Octal
- Value of Root 3
- XXXVII Roman Numerals
- Continuous Variable
- Different Forms Of The Equation Of Line
- Construction of Square
- Divergence Theorem
- Decimal Worksheets
- Cube Root 1 to 20
- Divergence Theorem
- Difference Between Simple Interest and Compound Interest
- Difference Between Relation And Function
- Cube Root Of 1728
- Decimal to Binary
- Cube Root of 216
- Difference Between Rows and Columns
- Decimal Number Comparison
- Data Management
- Factors of a Number
- Factors of 90
- Cos 360
- Factors of 96
- Distance between Two Lines
- Cube Root of 3
- Factors of 81
- Data Handling
- Convert Hexadecimal To Octal
- Factors of 68
- Factors of 49
- Factors of 45
- Continuity and Discontinuity
- Value of Pi
- Value of Pi
- Value of Pi
- Value of Pi
- 1 bigha in square feet
- Value of Pi
- Types of angles
- Total Surface Area of Hemisphere
- Total Surface Area of Cube
- Thevenin's Theorem
- 1 million in lakhs
- Volume of the Hemisphere
- Value of Sin 60
- Value of Sin 30 Degree
- Value of Sin 45 Degree
- Pythagorean Triplet
- Acute Angle
- Area Formula
- Probability Formula
- Even Numbers
- Complementary Angles
- Properties of Rectangle
- Properties of Triangle
- Co-prime numbers
- Prime Numbers from 1 to 100
- Odd Numbers
- How to Find the Percentage?
- HCF Full Form
- The Odd number from 1 to 100
- How to find HCF
- LCM and HCF
- Calculate the percentage of marks
- Factors of 15
- How Many Zeros in a Crore
- How Many Zeros are in 1 Million?
- 1 Billion is Equal to How Many Crores?
- Value of PI
- Composite Numbers
- 100 million in Crores
- Sin(2x) Formula
- The Value of cos 90°
- 1 million is equal to how many lakhs?
- Cos 60 Degrees
- 1 Million Means
- Rational Number
- a3-b3 Formula with Examples
- 1 Billion in Crores
- Rational Number
- 1 Cent to Square Feet
- Determinant of 4×4 Matrix
- Factor of 12
- Factors of 144
- Cumulative Frequency Distribution
- Factors of 150
- Determinant of a Matrix
- Factors of 17
- Bisector
- Difference Between Variance and Standard Deviation
- Factors of 20
- Cube Root of 4
- Factors of 215
- Cube Root of 64
- Cube Root of 64
- Cube Root of 64
- Factors of 23
- Cube root of 9261
- Cube root of 9261
- Determinants and Matrices
- Factors of 25
- Cube Root Table
- Factors of 28
- Factors of 4
- Factors of 32
- Differential Calculus and Approximation
- Difference between Area and Perimeter
- Difference between Area and Volume
- Cubes from 1 to 50
- Cubes from 1 to 50
- Curved Line
- Differential Equations
- Difference between Circle and Sphere
- Cylinder
- Difference between Cube and Cuboid
- Difference Between Constants And Variables
- Direct Proportion
- Data Handling Worksheets
- Factors of 415
- Direction Cosines and Direction Ratios Of A Line
- Discontinuity
- Difference Between Fraction and Rational Number
- Difference Between Line And Line Segment
- Discrete Mathematics
- Disjoint Set
- Difference Between Log and Ln
- Difference Between Mean, Median and Mode
- Difference Between Natural and whole Numbers
- Difference Between Qualitative and Quantitative Research
- Difference Between Parametric And Non-Parametric Tests
- Difference Between Permutation and Combination
Frequently Asked Questions on Direct Proportion
Direct proportion means that as one quantity increases, the other quantity also increases by the same rate. For example, the more hours you work, the more money you earn.
The formula for direct proportion is y = kx, where y and x are the two quantities, and k is a constant that represents their proportional relationship.
A direct proportion is a relationship between two quantities where one quantity increases or decreases at the same rate as the other. This means the ratio between the two quantities remains constant.
If A and B are directly proportional, it means that as A increases, B also increases by the same rate. The ratio between A and B remains constant. This can be expressed as A ∝ B or A = kB, where k is the constant of proportionality.
Direct proportion: The more hours you work, the more money you earn. Indirect proportion: The more people working on a task, the less time it takes to complete.