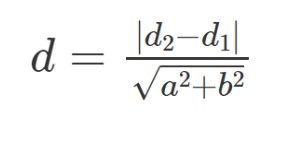The distance between two lines in three-dimensional space is the shortest length between them. This is a key idea in math and is useful in many areas like computer graphics, engineering, and physics.
To find this distance, you need to locate a point on each line and then measure the shortest path between these points. This process uses methods from vector algebra and linear algebra.
What is the distance between two lines?
The distance between two lines in mathematics is the shortest distance between them in a three-dimensional space. If the lines are parallel, this distance is the shortest distance between any two points on each line.
Calculating the distance between two lines is important in fields like computer graphics, engineering, and physics. Understanding vector arithmetic, including dot products and cross products, is necessary to find this distance.
Distance between Two Straight Lines
The distance between two straight lines can either be finite or infinite, based on whether the lines are parallel or not. For parallel lines, the distance is the shortest distance between any two points on each line. For lines that are not parallel, the distance is a finite value that represents the shortest distance between them.
In geometry, we often deal with different sets of lines such as
1.) Distance between Two Parallel Lines
The distance between two parallel lines is measured as the perpendicular distance from any point on one line to the other line. This distance can be found by projecting a point from one line onto the other line and then measuring the distance between these two points. The distance between two parallel lines remains constant, no matter where the lines are located or which points are used for the calculation.
2.) Distance between Two Intersecting Lines
The distance between two intersecting lines is zero, as these lines cross each other at a single point. The point of intersection is the only location where the distance between the two lines is zero.
3.) Distance between Two Skew Lines
In a three-dimensional space, the distance between two skew lines is the shortest distance between them. Skew lines do not intersect and are not parallel, and the distance between them is a finite value.
Steps to Calculate the Distance Between Two Lines
Here are the steps to calculate the distance between two lines in a two-dimensional space represented by the equation "y = mx + c":
- Represent the Lines: Write the equations of the lines in the slope-intercept form "y = mx + c", where "m" is the slope and "c" is the y-intercept.
- Find the Perpendicular Line: Determine the equation of the perpendicular line segment connecting the two lines. The slope of the perpendicular line is the negative reciprocal of the original line's slope. The equation of the perpendicular line is "y = -1/m * x + b", where "b" is the y-intercept.
- Find the Intersection Point: Calculate the point of intersection by setting the two line equations equal to each other and solving for x and y.
- Use the Distance Formula: Apply the distance formula "d = √((x2 - x1)^2 + (y2 - y1)^2)" to find the distance between the point of intersection and the nearest point on each line.
- Repeat for Multiple Points: Repeat the above process for multiple points on each line to ensure you find the shortest distance between the two lines.
In summary, the distance between two lines represented by "y = mx + c" can be calculated using basic algebra and the distance formula. The steps involve representing the lines in slope-intercept form, finding the perpendicular line, determining intersection points, and applying the distance formula to find the shortest distance.
Distance Between Two Lines Formula
In three-dimensional space, the formula for the distance between two lines depends on whether the lines are parallel, intersecting, or skew. Here are the formulas for each case:
- Parallel Lines: Use the formula for the shortest distance between parallel lines.
- Intersecting Lines: If the lines intersect, the distance is zero.
- Skew Lines: Use the formula specific to skew lines, which considers the direction vectors of the lines.
Here are the formulas for distance between two line:
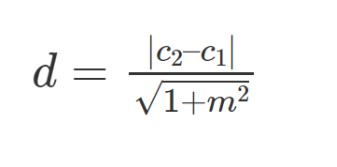
The formula for the Distance Between Two Parallel Lines are:
Frequently Asked Questions
The formula for two parallel lines is y = mx + c1 and y = mx + c2, where m is the common slope and c1 and c2 are the y-intercepts of the two lines.
The shortest distance between two parallel lines is the perpendicular distance between them, given by the formula d = |c1 - c2| / √(a^2 + b^2), where a, b, c1, and c2 are the coefficients of the line equations.
To find the distance between two non-parallel lines, you need to find the point of intersection of the lines and then calculate the perpendicular distance from that point to each line. This involves solving a system of linear equations.
To find the distance between parallel lines, you need to use the formula d = |c1 - c2| / √(a^2 + b^2), where a, b, c1, and c2 are the coefficients of the line equations. This gives the perpendicular distance between the two parallel lines.
What is the formula for distance between two lines?
The formula for the distance between two lines is d = |a1x1 + b1y1 + c1| / √(a1^2 + b1^2), where (x1, y1) is a point on the first line and a1, b1, c1 are the coefficients of the first line equation.