Mensuration

Complete Guide to Mensuration: Formulas, Concepts & Applications

Introduction to Mensuration

Mensuration is the fundamental branch of mathematics that deals with the measurement of geometric magnitudes including length, area, volume, and various parameters of geometric objects. The term derives from the Latin word "mensura," meaning "to measure." This mathematical discipline forms the foundation for numerous real-world applications, from architecture and engineering to everyday problem-solving scenarios.

Understanding mensuration empowers students to calculate the dimensions of shapes and solids with precision, making it an indispensable skill in both academic and practical contexts. Whether determining the amount of paint needed to cover a wall, calculating the capacity of a water tank, or designing architectural structures, mensuration provides the mathematical framework necessary for accurate measurements.

The study of mensuration encompasses two primary categories: plane mensuration (dealing with two-dimensional figures like rectangles, triangles, and circles) and solid mensuration (focusing on three-dimensional objects such as cubes, cylinders, and spheres). Mastery of mensuration concepts enables students to transition smoothly from basic geometric understanding to advanced applications in calculus, physics, and engineering disciplines.

Understanding Dimensions in Mensuration

In mensuration, dimension refers to a direction in which one can measure distance. The concept of dimensions is fundamental to understanding how we quantify different aspects of geometric objects:

One-Dimensional (1D) Measurement

Length represents size in one dimension—the amount of linear distance between two points. Examples include the length of a line segment, the circumference of a circle (as a one-dimensional measurement wrapped around), or the distance along a path. One-dimensional measurements answer the question: "How long is it?"

Two-Dimensional (2D) Measurement

Area quantifies size in two dimensions, representing the amount of surface enclosed within a boundary. Think of area as the amount of paper or material needed to cover a shape completely. Two-dimensional measurements answer: "How much surface does it cover?" Common 2D shapes include rectangles, triangles, circles, and polygons.

Three-Dimensional (3D) Measurement

Volume measures size in three dimensions, indicating the amount of space occupied by an object or the capacity of a container. Volume calculations answer: "How much space does it take up?" or "How much can it hold?" Three-dimensional objects include cubes, cylinders, spheres, cones, and pyramids.

Practical Understanding

Consider a swimming pool: its length and width (2D) determine the surface area for covering, while adding depth (3D) allows us to calculate the volume of water it can hold. This hierarchical understanding from length to area to volume forms the conceptual backbone of mensuration studies.

Comprehensive Mensuration Formulas

2D Shapes (Plane Figures)

Shape	Area Formula	Perimeter Formula	Key Parameters
Rectangle	A = l × b	P = 2(l + b)	l = length, b = breadth
Square	A = l²	P = 4l	l = side length
Triangle (Base-Height)	A = ½ × b × h	P = a + b + c	b = base, h = height, a,b,c = sides
Triangle (Heron's Formula)	A = √[s(s-a)(s-b)(s-c)]	P = a + b + c	s = semi-perimeter = (a+b+c)/2
Parallelogram	A = l × h	P = 2(l + b)	l = length, h = perpendicular height, b = breadth
Trapezium	A = ½(a + b) × h	P = sum of all sides	a, b = parallel sides, h = height
Rhombus	A = ½ × d₁ × d₂	P = 4l	d₁, d₂ = diagonals, l = side length
Kite	A = ½ × d₁ × d₂	P = 2(a + b)	d₁, d₂ = diagonals, a, b = non-adjacent sides
Circle	A = πr² = πd²/4	Circumference = 2πr = πd	r = radius, d = diameter
Sector of Circle	A = (θ/360°) × πr² = r²θ/2 (θ in radians)	Arc length = (θ/360°) × 2πr = rθ	θ = central angle, r = radius
Segment of Circle	A = r²(θ - sin θ)/2	-	θ = central angle (radians), r = radius

3D Shapes (Solid Figures)

Shape	Volume Formula	Surface Area Formula	Key Parameters
Cube	V = l³	TSA = 6l²	l = edge length
Cuboid (Rectangular Prism)	V = l × b × h	TSA = 2(lb + bh + lh)	l = length, b = breadth, h = height
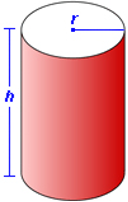
Cylinder	V = πr²h	CSA = 2πrh<br>TSA = 2πr(r + h)	r = base radius, h = height
Cone	V = ⅓πr²h	CSA = πrl<br>TSA = πr(r + l)	r = base radius, h = height, l = slant height
Sphere	V = 4πr³/3	TSA = 4πr²	r = radius
Hemisphere	V = 2πr³/3	CSA = 2πr²<br>TSA = 3πr²	r = radius

Key:

• TSA = Total Surface Area
• CSA = Curved Surface Area (Lateral Surface Area)
• LSA = Lateral Surface Area

Special Relationships and Derived Formulas

For Cuboid:

• Diagonal length = √(l² + b² + h²)

For Cube:

• Face diagonal = l√2
• Body diagonal = l√3

For Cylinder:

• When formed from rolling a rectangle: length becomes circumference, width becomes height

For Cone:

• Slant height: l = √(r² + h²)
• Relationship: l² = r² + h²

For Circle Segment:

• Chord length: c = 2√(r² - t²), where t = perpendicular distance from center to chord
• Segment height: h = r - t

Circle Mensuration: Special Cases

Circles possess unique properties that require specialized formulas. Understanding these relationships is crucial for solving complex mensuration problems.

Circle Fundamentals

The circumference of a circle represents its perimeter—the distance around the circular boundary. The relationship between circumference (C), diameter (d), and radius (r) is expressed through the mathematical constant π (pi ≈ 3.14159):

• C = 2πr = πd
• d = 2r (diameter is twice the radius)

The area of a circle can be calculated using either radius or diameter:

• A = πr²
• A = πd²/4

Arc Length and Sector Area

When working with portions of circles, two important concepts emerge:

Arc Length (s): The distance along the curved portion of the circle

• Formula: s = rθ (where θ is in radians)
• Formula: s = (θ/360°) × 2πr (where θ is in degrees)

Sector Area: The "pie-slice" portion of a circle

• Formula: A = r²θ/2 (θ in radians)
• Formula: A = (θ/360°) × πr² (θ in degrees)

Circle Segment

A segment is the region between a chord and the arc it subtends. The area calculation involves:

• A = r²(θ - sin θ)/2 (θ in radians)

For practical calculations involving segments:

• Chord length: c = 2√(r² - t²), where t is the perpendicular distance from center to chord
• Segment height: h = r - t

Solving Circle Problems: A Practical Example

Problem: Find the arc length of a circle with radius 15 cm when the central angle is 60°.

Solution:

1. Identify known values: r = 15 cm, θ = 60°
2. Determine the fraction of the circle: 60°/360° = 1/6
3. Calculate full circumference: C = 2π × 15 = 30π ≈ 94.248 cm
4. Find arc length: a = (1/6) × 94.248 = 15.7 cm

Alternatively, using the direct formula: a = (θ/360°) × 2πr = (60°/360°) × 2π × 15 = 15.7 cm

Practical Applications of Mensuration

Mensuration extends far beyond classroom exercises, serving as a critical tool in numerous real-world scenarios:

Architecture and Construction

• Material estimation: Calculating quantities of paint, wallpaper, tiles, or flooring materials
• Structural design: Determining load-bearing capacities based on volume and surface area
• Cost estimation: Pricing construction projects based on area coverage and volume requirements

Engineering Applications

• Capacity calculations: Designing water tanks, fuel containers, and storage facilities
• Fluid dynamics: Computing flow rates through pipes of various dimensions
• Manufacturing: Optimizing material usage to minimize waste

Agricultural Planning

• Land measurement: Determining plot areas for cultivation
• Irrigation design: Calculating water distribution requirements
• Fencing estimation: Computing perimeter measurements for boundary construction

Daily Life Applications

• Home improvement: Measuring rooms for carpeting, painting, or furniture placement
• Cooking and baking: Understanding volume measurements for recipes
• Packaging: Determining box sizes and shipping volumes

Example Problem: Garden Path Construction

Scenario: Mrs. Kaushik has a square plot measuring 25 m × 25 m. She constructs a house measuring 15 m × 20 m in the center and wants to develop a garden around it at Rs. 55 per m².

Solution:

1. Area of square plot = 25² = 625 m²
2. Area of house = 15 × 20 = 300 m²
3. Garden area = 625 - 300 = 325 m²
4. Total cost = 325 × 55 = Rs. 17,875

Common Mistakes and Problem-Solving Tips

Frequent Errors to Avoid

1. Unit Confusion Always ensure consistent units throughout calculations. Converting between cm, m, and km requires careful attention:

• 1 m = 100 cm
• 1 km = 1000 m
• 1 m² = 10,000 cm²
• 1 m³ = 1,000,000 cm³

2. Formula Selection Choose the appropriate formula based on given information:

• For triangles: Use base-height formula when height is known; use Heron's formula when only sides are given
• For circles: Distinguish between problems requiring circumference, area, arc length, or sector area

3. Dimensional Analysis

• Area results should have squared units (cm², m²)
• Volume results should have cubic units (cm³, m³, liters)
• Perimeter/circumference should have linear units (cm, m)

4. π (Pi) Approximation

• Use π = 22/7 for simpler calculations or when specifically instructed
• Use π = 3.14159... or calculator π button for greater precision
• Be consistent with the approximation throughout a problem

Problem-Solving Strategy

Step 1:Visualize and Sketch Draw a diagram representing the problem, labeling all known measurements.

Step 2:Identify Requirements Determine what the question asks for: area, volume, perimeter, or surface area?

Step 3:Select Appropriate Formula Match the shape and given information to the correct formula from your reference chart.

Step 4:Substitute and Calculate Carefully substitute values into the formula, maintaining unit consistency.

Step 5:Verify Reasonableness Check if your answer makes logical sense in the context of the problem.

Example: Trapezium Area Problem

Problem: A trapezium has an area of 34 cm² and one parallel side of 10 cm. If the height is 4 cm, find the other parallel side.

Solution:

• Formula: A = ½(a + b) × h
• Substituting: 34 = ½(10 + b) × 4
• Simplifying: 34 = 2(10 + b)
• 34 = 20 + 2b
• 2b = 14
• b = 7 cm

Mensuration in Different Curricula

Mensuration Class 8

Students in Class 8 are introduced to fundamental mensuration concepts:

• 2D shapes: Areas and perimeters of rectangles, squares, triangles, and circles
• Basic 3D shapes: Surface areas and volumes of cubes and cuboids
• Practical applications: Simple word problems involving measurements
• Key topics: Understanding the relationship between dimensions and measurements

Class 8 Focus Areas:

• Converting between different units of measurement
• Calculating the area of composite figures by breaking them into simpler shapes
• Understanding the concept of surface area versus volume
• Introduction to Heron's formula for triangle area

Mensuration Class 9

Class 9 curriculum expands to more complex shapes and applications:

• Advanced 2D shapes: Trapeziums, rhombus, parallelograms, and their properties
• Circular geometry: Sectors, segments, and arc lengths
• Surface areas: Cylinders, cones, and spheres
• Volume calculations: Understanding capacity and displacement
• Heron's formula applications: Problems involving triangles with only side lengths known

Class 9 Advanced Topics:

• Combination of solids and their mensuration
• Problems involving conversion from one shape to another (e.g., melting and recasting)
• Surface area problems with open and closed containers
• Practical applications in construction and design

Mensuration Class 10

Class 10 introduces higher-level concepts and complex problem-solving:

• Frustum of cone: Surface area and volume calculations
• Combination of solids: Objects formed by combining multiple shapes
• Conversion problems: Transforming one solid into another while preserving volume
• Advanced applications: Real-world scenarios requiring multi-step solutions

Mensuration Formula Chart

A mensuration formula chart serves as a quick reference guide containing all essential formulas organized by shape category. Students should maintain such charts for:

• Rapid formula recall during examinations
• Homework and assignment completion
• Competitive exam preparation

Mensuration Formula in Hindi (मेन्सुरेशन फॉर्मूला हिंदी में)

For Hindi-medium students, understanding mensuration terminology in Hindi is crucial:

द्विविमीय आकृतियाँ (2D Shapes):

• आयत (Rectangle): क्षेत्रफल = लंबाई × चौड़ाई, परिमाप = 2(लंबाई + चौड़ाई)
• वर्ग (Square): क्षेत्रफल = भुजा², परिमाप = 4 × भुजा
• त्रिभुज (Triangle): क्षेत्रफल = ½ × आधार × ऊँचाई
• वृत्त (Circle): क्षेत्रफल = πr², परिधि = 2πr

त्रिविमीय आकृतियाँ (3D Shapes):

• घनाभ (Cuboid): आयतन = लंबाई × चौड़ाई × ऊँचाई
• घन (Cube): आयतन = भुजा³, पृष्ठीय क्षेत्रफल = 6 × भुजा²
• बेलन (Cylinder): आयतन = πr²h, वक्र पृष्ठीय क्षेत्रफल = 2πrh
• शंकु (Cone): आयतन = ⅓πr²h, वक्र पृष्ठीय क्षेत्रफल = πrl

Conclusion

Mensuration forms an indispensable component of mathematical education, bridging theoretical geometry with practical real-world applications. Mastery of mensuration formulas and concepts enables students to solve complex spatial problems, estimate materials accurately, and develop critical analytical thinking skills.

This comprehensive guide has covered fundamental definitions, extensive formula collections, practical problem-solving techniques, and curriculum-specific insights for Classes 8, 9, and 10. Regular practice with diverse problem types—from simple area calculations to complex volume transformations—will solidify understanding and build confidence in applying mensuration principles.

Remember that successful mensuration problem-solving requires:

1. Clear visualization of the geometric situation
2. Accurate formula selection based on given information
3. Careful calculation with consistent units
4. Logical verification of results

Mensuration CBSE Note Theory

Some important terms

Mensuration:

The study of the measurement of geometric magnitudes such as length.

Dimension:

A dimension is a direction in which one can measure distance. For example, “horizontal” or “left and right” is a dimension.

Length is the size in one dimension.It could be the amount of string needed to cover a line.

Area is the size in two dimensions.It could be the amount of paper needed to cover a shape.

SOME IMPORTANT FORMULAE

1. Area of rectangle (A) = length(l) × Breadth(b), A = l × b
2. Perimeter of a rectangle (P) = 2 × (Length(l) + Breadth(b)), P = 2 × (l + b)
3. Area of a square (A) = Length (l) × Length (l), A = l × l
4. Perimeter of a square (P) = 4 × Length (l), P = 4 × l
5. Area of a parallelogram (A) = Length(l) × Height(h), A = l × h

   

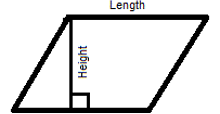
6. Perimeter of a parallelogram (P) = 2 × (length(l) + Breadth(b)), P = 2 × (l + b)
7. Area of a triangle (A) = (Base(b) × Height(h)) / 2, A = (1/2) × b × h

   

   
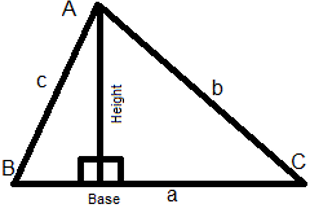
   And for a triangle with sides measuring “a”, “b” and “c”, Perimeter = a + b + c
   and s = semi perimeter = perimeter / 2 = (a+b+c)/2
   And also . Area of triangle = A = √s(s – a)(s – b)(s – c)
   This formula is also known as “Hero’s formula”.
8. Area of triangle (A) =
   Where, A, B and C are the vertex and angle A, B, C are respective angles of triangle and a, b, c are the respective opposite sides of the angles as shown in figure below:
   
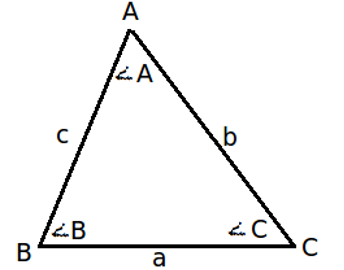
9. Area of isosceles triangle =(b/4) √(4a² – b²)
   Where, a = length of two equal side, b = length of base of isosceles triangle.
10. Area of trapezium (A) =1/2 (a + b) × h
    Where, “a” and “b” are the length of parallel sides and “h” is the perpendicular distance between “a” and “b”.
    

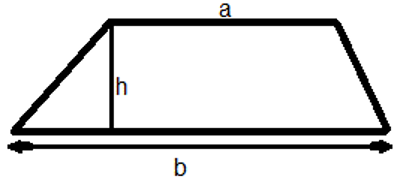
11. Perimeter of a trapezium (P) = sum of all sides

12. Area of rhombus (A) = Product of diagonals / 2
13. Perimeter of a rhombus (P) = 4 × l where l = length of a side
14. Area of quadrilateral (A) = 1/2 × Diagonal × (Sum of offsets)

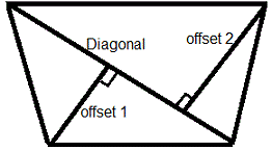
15. Area of a Kite (A) = 1/2 × product of it's diagonals
16. Perimeter of a Kite (A) = 2 × Sum on non-adjacent sides
17. Area of a Circle (A) = πr² = (πd² / 4)
    Where, r = radius of the circle and d = diameter of the circle.
18. Circumference of a Circle = 2πr = πd
    r = radius of circle
    d = diameter of circle

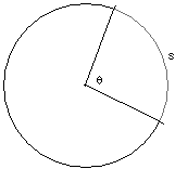
Solving for circle arc length.
s = r × θ

Circle 

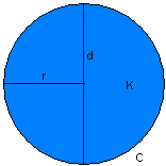
Circle Formula Reference

d = 2r	diameter
r = d/2	radius
C = 2πr	circumference
r = C/2π	radius

C = π × d	circumference
d = C/π	diameter

C = 2√π×K	circumference
K = C²/4π	area

K = πr²	area
r = √(K/π)	radius

K = π × d² / 4	area
r = √(4 × K / π)	diameter

K = C x r/2	area
C = 2 x K/r	circumference
r = 2 x K/C	radius

Segment of Circle

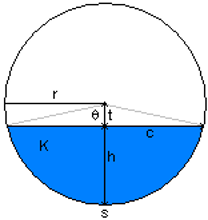
c = 2√(r2 − t2)	chord length
r = √((c2/4) + t2	circle radius
t = √(r2 − c2/4)	circle center to chord midpoint distance

K = r2(θ − sin θ)⁄2	segment area
r = √(2 × K / (θ − sin θ))	circle radius

θ = s/r	central angle
s = θ × r	arc length
r = s/θ	circle radius

h = r − t	segment height
r = h + t	circle radius
t = r − h	circle center to chord midpoint distance

 

SECTOR OF A CIRCLE:

A sector of a circle is a pie-shaped region bounded by an arc and an angle.
On this page we'll show you how to find the arc length a and the area A of the sector.

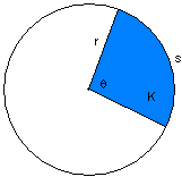
K = r2 × θ / 2	sector area
r = √(2 × K / θ)	circle radius
θ = 2 × K / r2	central angle

ARC OF A CIRCLE:

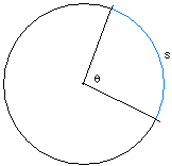
S = r × θ	arc length
r = s / θ	circle radius
θ = s / r	central angle

We'll use a circle with radius 15 cm and central angle 60°.

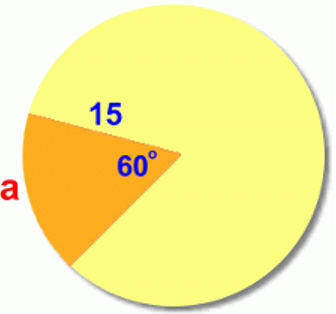
The first step is to find out what fraction of the circle is represented by the central angle 60°:

 60/360 = 0.16

The sector represents 1/6 of the circle, or 0.1666... of the circle.

To find the arc length a, we now need to find the circumference (the distance around the full circle), and then find 1/6 of it (multiply it by 0.1666...) 

This is the length of the arc a.

C = 2πr

= 2π . 15

= 94.248

a = 0.16 94.248 cm

= 15.7 cm

This method will work for any sector in any circle. You just need to find the fraction of the circle that the sector angle represents, and then find that fraction of the circumference.

A = θ/360 = 2πr 

Here's a quicker formula to use, that summarizes what we did in one calculation.

CUBE:

If all three lengths are equal it can be called a cube and each face will be a square.

A cube is still a prism.

And a cube is one of the Platonic Solids.

A cuboid is a box-shaped object.

It has six flat sides and all angles are right angles.

And all of its faces are rectangles.

It is also a prism because it has the same cross-section along a length. In fact it is a rectangular prism.

VOLUME AND SURFACE AREA:

The volume of a cuboid is found using the formula:
Volume = Height × Width × Length
Which is usually shortened to:
V = h × w × l
Or more simply:

V = hwl

(To remember, think "howl")

SURFACE AREA:

And the surface area is found using the formula:
A = 2wl + 2lh + 2hw

Ex: Find the volume and surface area of this cuboid.

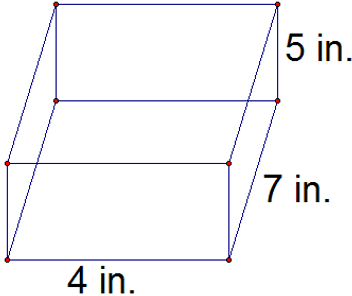
V = 5 × 4 × 7 = 140
A = 2 × 5 × 4 + 2 × 4 × 7 + 2 × 7 × 5
= 40 + 56 + 70 = 166

CONES:

If one end of a line is rotated about a second fixed line while keeping the line's other end fixed, then a cone is formed. The point about which the line is rotated is called the vertex and the base of the cone is a circle.

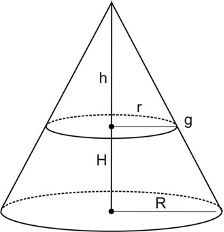
A cone is said to be right when the vertex is directly above the centre of the base.

CYLINDERS:

If a line is rotated about a second fixed line while keeping both lines parallel, then a cylinder is formed.