Ellipse

Equation of an Ellipse in Standard Form

Standard Form: x²/a² + y²/b² = 1

where b² = a²(1 - e²), Here b < a.

Some Terms Related to an Ellipse

Let the equation of ellipse be x²/a² + y²/b² = 1 (a > b)

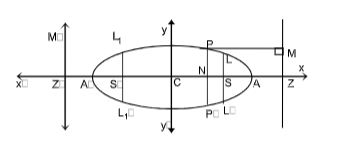
• Centre

All chords passing through centre C are bisected at C.

Here C ≡ (0, 0).

• Foci

S and S' are two foci of the ellipse and their co-ordinates are (ae, 0) and (–ae, 0) respectively.

• Directrices

ZM and Z'M' are two directrices of the ellipse and their equations are x = a/e and x = -a/e.

• Axes

The lines AA' and BB' are called major and minor axes respectively of the ellipse. AA' = 2a and BB' = 2b.

• Double ordinates

Let P be a point on the ellipse. If we draw PN ⊥ to the axes of ellipse and produce it to meet the curve again at P' then PNP' is called a double ordinate.

• Latus rectum

The chord through a focus at right angle to the major axis is called the Latus Rectum. Here LSL' and L₁S'L₁' are the latus rectum of the ellipse.

L ≡ (ae, b²/a); L' ≡ (ae, -b²/a)
L₁ ≡ (-ae, b²/a); L₁' ≡ (-ae, -b²/a)

Equations of latus rectum are x = ±ae.

• Focal Chord

The chord of the ellipse passing through its focus is called a focal chord.

• Vertices

The points where the major axis of the ellipse meets it are called its vertices. Here A(a, 0) and A'(–a, 0) are the vertices of the ellipse.

Focal Distance of a Point

Let P(x, y) be a point on the ellipse. Then

• SP = ePN = e(a/e - x) = a - ex
• S'P = eP'N' = e(a/e + x) = a + ex
• SP + S'P = 2a

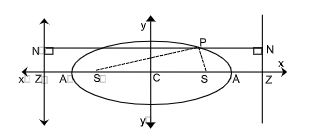
∴ the sum of the focal distances of any point on the ellipse is equal to length of its major axis.

Illustration 1: The equation of the ellipse whose foci are (2, 3) and (–2, 3) and whose semi-minor axis is √5 is

(A) 9x² + 5y² – 54x + 36 = 0 (B) 5x² + 9y² – 54x + 36 = 0

(C) 5x² + 9y² – 54y + 36 = 0 (D) none of these

Solution (C):

Here S ≡ (2, 3), S' ≡ (–2, 3), b = √5 ∴ SS' = 4 ⇒ 2ae = 4 ⇒ ae = 2.

Now, b² = a²(1 - e²) ⇒ 5 = a² - a²e² ⇒ 5 = a² - 4 ⇒ a = 3.

If P(x, y) be any point on the ellipse then by property of ellipse, SP + S'P = 2a

or, √[(x-2)² + (y-3)²] + √[(x+2)² + (y-3)²] = 6 ...(i)

After simplification: 5x² + 9y² – 54y + 36 = 0. This is the required equation of the ellipse.

Other Forms

If in the equation x²/a² + y²/b² = 1, when a < b i.e. a² < b², then the major and minor axes of the ellipse lie along the y and x-axes and are of lengths 2b and 2a respectively. Here AA' = 2b and BB' = 2a. The foci S and S' are (0, be) and (0, –be) respectively. The directrices ZM and Z'M' are y = b/e and y = -b/e respectively. Eccentricity is given by a² = b²(1 - e²).

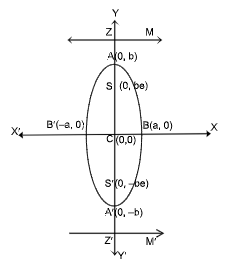
Diagram Description: A coordinate system showing an ellipse with major axis along y-axis, vertices at A(0, b) and A'(0, -b), minor axis along x-axis with vertices at B(-a, 0) and B(a, 0), foci at S(0, be) and S'(0, -be), and directrices at y = ±b/e.

• If the centre of the ellipse be taken as (h, k) and axes parallel to x and y-axes, then the equation of the ellipse is (x-h)²/a² + (y-k)²/b² = 1.

Difference between ellipses in two forms (i.e. when a > b and a < b)

Property	x²/a² + y²/b² = 1, a > b	x²/a² + y²/b² = 1, a < b
Centre	(0, 0)	(0, 0)
Vertices	(±a, 0)	(0, ±b)
Length of Major Axis	2a	2b
Length of Minor Axis	2b	2a
Foci	(±ae, 0)	(0, ±be)
Equation of directrices	x = ±a/e	y = ±b/e
Relation in a, b and e	b² = a²(1 - e²)	a² = b²(1 - e²)
Length of Latus Rectum	2b²/a	2a²/b
Ends of Latus Rectum	(±ae, ±b²/a)	(±a²/b, ±be)
Distance between foci	2ae	2be
Distance between directrices	2a/e	2b/e
Focal radii	SP = a - ex₁ & S'P = a + ex₁	SP = b - ey₁ & S'P = b + ey₁
Sum of Focal radii SP + S'P =	2a	2b

Illustration 2: The equation of ellipse referred to its centre whose foci are the points (4, 0) and (–4, 0) and whose eccentricity is 1/3 is

(A) x²/144 + y²/128 = 1

(B) x²/128 + y²/12 = 1

(C) x²/128 + y²/144 = 1

(D) none of these

Solution (A):

Let the equation to the ellipse be x²/a² + y²/b² = 1 ...(1)

Distance between the foci = 2ae = 4 + 4 = 8 ...(2)

Putting the value of e = 1/3 in (2), a = 4/e = 12

Again b² = a²(1 – e²) = 144(1 – 1/9) = 128

Put in (1) we have x²/144 + y²/128 = 1 ⇒ 8x² + 9y² = 1152

Exercise 1:

1. The equation of the ellipse referred to its centre whose latus-rectum is 5 and whose eccentricity is 2/3 is
   (A) 4x²/81 + 4y²/25 = 1 (B) 4x²/81 + 4y²/45 = 1
   (C) 4x²/9 + y²/16 = 1 (D) none of these
2. The eccentricity of the ellipse 12x² + 4y² + 24x – 16y + 25 = 0 is
   (A) √2/3 (B) 2/3 (C) 1/3 (D) 2/√5

Position of a Point Relative to an Ellipse

The point P(x₁, y₁) is outside or inside or on the ellipse x²/a² + y²/b² = 1, according as the quantity

S₁ ≡ x₁²/a² + y₁²/b² - 1

is positive or negative or zero.

Parametric DEquation

Clearly, x = a cos θ, y = b sin θ satisfy the equation x²/a² + y²/b² = 1 for all real values of θ.

Hence (a cos θ, b sin θ) is always a point on the ellipse x²/a² + y²/b² = 1 for any real value of θ.

Auxiliary Circle and Geometric Meaning of Eccentric Angle of a point:

The circle described on the major axis of an ellipse as diameter is called the auxiliary circle of the ellipse.

We draw a circle with AA' (the major axis) as the diameter. This circle is called the auxiliary circle of the ellipse. The equation of the circle is x² + y² = a². We draw ∠ACQ = θ.

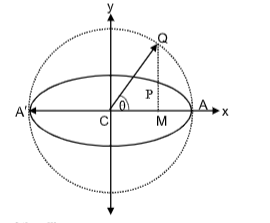
Diagram Description: A coordinate system showing an ellipse with its auxiliary circle (larger circle with radius a), where a point P on the ellipse corresponds to point Q on the auxiliary circle through the eccentric angle θ measured from the center C.

Illustration 3: The eccentric angles of the extremities of latus rectum of the ellipse x²/a² + y²/b² = 1 are

(A) x²/a² + y²/b² = 1 (B) (x₁, y₁)

(C) θ = tan⁻¹(±be/a) (D) θ = tan⁻¹(±b/ae)

Solution (D):

The co-ordinates of the end points of latus recta of the given ellipse are (±ae, ±b²/a).

Let θ be the eccentric angle of an end of a latus-rectum say (ae, b²/a) of the ellipse x²/a² + y²/b² = 1. Then its co-ordinates are (a cos θ, b sin θ).

∴ a cos θ = ae and b sin θ = b²/a.

⇒ (b sin θ)/(a cos θ) = (b²/a)/(ae) = b/ae

⇒ tan θ = b/ae ⇒ θ = tan⁻¹(b/ae)

Similarly, eccentric angle of other end of latus rectum is given by θ = tan⁻¹(-b/ae)

Hence, the eccentric angles of the extremities of the latus recta of the ellipse x²/a² + y²/b² = 1 are given by θ = tan⁻¹(±b/ae).

Equation of the Tangent in Various Forms

1. Point Form: xx₁/a² + yy₁/b² = 1
2. Parametric Form: (x cos θ)/a + (y sin θ)/b = 1
3. Slope Form: y = mx ± √(a²m² + b²) for all finite values of m.

Illustration 4: The locus of the foot of the perpendicular drawn from centre upon any tangent to the ellipse (x + y - 2)²/9 + (x - y)²/16 = 1 is

(A) x² + y² = a²x² + b²y² (B) (x² + y²)² = a²x² + b²y²

(C) (x - 0)² + (y - 0)² = 4² i.e. x² + y² = 16 (D) none of these

Solution (B):

Any tangent of x²/a² + y²/b² = 1 is y = mx ± √(a²m² + b²) ...(i)

Equation of line perpendicular to (i) and passing through (0, 0) is y = -x/m or x + my = 0 ...(ii)

Substituting the value of m from (ii) in (i), we get

y = -x/y · x ± √(a²(-x/y)² + b²)

∴ (x² + y²)² = a²x² + b²y².

Equation of the Normal in Various Forms

1. Point Form: y - y₁ = (a²y₁)/(b²x₁)(x - x₁) or (x - x₁)/(x₁/a²) = (y - y₁)/(-y₁/b²)
2. Parametric Form: (ax)/(cos θ) - (by)/(sin θ) = a² - b²

• Director Circle: x² + y² = a² + b².
• Chord of Contact: Equation of chord of contact drawn from point (x₁, y₁) is T = 0.
• Chord with Mid-point

Equation of the chord with mid point (x₁, y₁): T = S₁.

where T = xx₁/a² + yy₁/b² - 1, S = x²/a² + y²/b² - 1 and S₁ = x₁²/a² + y₁²/b² - 1.

Exercise 2:

1. The length of chord of the ellipse x²/25 + y²/16 = 1, whose middle point is (1/2, 2/5) is
   (A) (7√41)/10 (B) (7√41)/5 (C) (14√41)/5 (D) none of these
2. If the normal at the point P(θ) to the ellipse 5x² + 14y² = 70 intersects it again at the point Q(2θ), then
   (A) cos θ = -2/3 (B) sin θ = -2/3 (C) sin θ = -1/3 (D) none of these

Answer to Exercises

Exercise 1: (i) B (ii) B

Exercise 2: (i) B (ii) A

Formulae and Concepts at a Glance

1. For the ellipse x²/a² + y²/b² = 1, eccentricity is √(a² - b²)/a and foci are (±ae, 0).
2. Length of the latus rectum is 2b²/a.
3. Equation of tangent at (x₁, y₁) is xx₁/a² + yy₁/b² = 1.
4. Equation of normal at (x₁, y₁) is (a²x)/x₁ - (b²y)/y₁ = a² - b².
5. The line y = mx + c touches the ellipse x²/a² + y²/b² = 1 for c² = a²m² + b².
6. Locus of the point of intersection of perpendicular tangents to the ellipse is the director circle x² + y² = a² + b².
7. Parametric equation of the ellipse are x = a cos θ, y = b sin θ.
8. If P is any point on the ellipse and S, S' are its foci, then PS + PS' = 2a = length of the major axis.

Solved Examples

1. The distance between the directrices of the ellipse x²/4 + y²/9 = 1 is

(A) 9/5

(B) 24/5

(C) 18/5

(D) none of these

Sol. (C). 4 = 9(1-e²) ⇒ e = 5/3.

Distance between directrices = 2b/e = 2×3/(5/3) = 18/5.

2. If a tangent of slope 'm' at a point of the ellipse x²/a² + y²/b² = 1 passes through (2a, 0) and if 'e' denotes the eccentricity of the ellipse, then

(A) m² + e² = 1

(B) 2m² + e² = 1

(C) 3m² + e² = 1

(D) none of these

Sol. (C). Tangent of slope m is y = mx ± √(a²m² + b²). Passes through (2a,0): 3a²m² = b² ⇒ 3m² = 1 - e².

3. The locus of a variable point whose distance from the point (5, 2) is 1/4 times its distance from the line 2x + 3y = 5 is

(A) circle

(B) hyperbola

(C) ellipse

(D) parabola

Sol. (C) As eccentricity e < 1, locus is an ellipse.

4. If F₁ (0,0), F₂(3,4) and |PF₁| + |PF₂| = 10, then the locus of P is

(A) ellipse

(B) straight line

(C) hyperbola

(D) line segment

Sol. (A). As sum of distances is constant and greater than F₁F₂, locus is an ellipse.

5. If the normal at any point P of the ellipse x²/a² + y²/b² = 1 meets the axes in G and g respectively, then |PG| : |Pg| is equal to

(A) a : b

(B) a² : b²

(C) b² : a²

(D) b : a

Sol. (C) At P(a cosθ, b sinθ), the normal meets axes in G(a²/b cosθ, 0), g(0, b²/a sinθ, 0). PG = b²/(a²), so ratio is b² : a².

6. P is a variable point on x²/a² + y²/b² = 1 with AA′ as the major axis. Then the maximum value of the area of the triangle APA′ is

(A) ab

(B) 2ab

(C) ab/2

(D) none of these

Sol. (A) Area ΔAPA′ is maximum when height = b. Area = ½·2a·b = ab.

[Triangle APA' on ellipse, with max altitude = b]

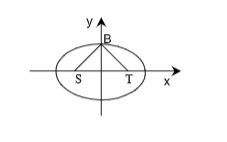
7. S and T are the foci of an ellipse and B is an end of the minor axis. If STB is an equilateral triangle, then the eccentricity of the ellipse is

(A) 1/4

(B) 1/3

(C) 1/2

(D) 2/3

Sol. (C) e² = 1/4 ⇒ e = 1/2.

8. The line x + 2y − 4 = 0 and the ellipse 3x² + 4y² = 12 meet in

(A) a unique point

(B) no point

(C) two distinct points

(D) none of these

Sol. (C) Substituting y, you get a quadratic with two (equal) roots: x = 1 (multiplicity 2), so two coincident points.

9. A circle is drawn on the major axis of 9x²+16y²=144 as diameter. The equation of the circle is

(A) x² + y² = 4

(B) x² + y² = 3

(C) x² + y² = 16

(D) x² + y² = 9

Sol. (C) The ellipse has ends A′(−4, 0), A(4, 0), so a = 4, radius = 4. Equation: x² + y² = 16.

10. The centre of the ellipse ((x−1)/3)² + ((y−1)/4)² = 1 is

(A) (0, 0)

(B) (1, 1)

(C) (1, 0)

(D) (0, 1)

Sol. (B) This is the standard ellipse with center at (1, 1).

Assignment

1. The angle between pair of tangents drawn to the ellipse 3x² + 2y² = 5 from the point (1,2) is

   (A) tan⁻¹12/5

   (B) tan⁻¹6/5

   (C) tan⁻¹(12/5)

   (D) tan⁻¹(12 5)

2. The equation (10x−5)² + (10y−5)² = (3x+4y−1)² represents

   (A) a pair of straight lines

   (B) an ellipse

   (C) a hyperbola

   (D) a circle

3. The equation of the ellipse whose focus is (1,−1), directrix x−y−3=0, and eccentricity 1/2 is

   (A) 7x²+2xy+7y²−10x+10y+7=0

   (B) 7x²+2xy+7y²+7=0

   (C) 7x²+2xy+7y²+10x−10y−7=0

   (D) none of these.

4. The radius of the circle passing through the foci of x²/16 + y²/9 = 1, centered at (0,3), is

   (A) 4

   (B) 3

   (C) 12

   (D) 7/2

5. If the ellipse x²/2 + y²/1 = 1 meets the ellipse x²/1 + y²/a² = 1 (a>1) in n points, then

   (A) n=2

   (B) n=4

   (C) n=0

   (D) none of these.

6. The straight line x+y=a will be a tangent to x²/9 + y²/16 = 1 if a is

   (A) 8

   (B) ±5

   (C) ±10

   (D) ±6

7. Equation of the ellipse with eccentricity 1/2 and foci at (±1,0) is

   (A) x²/3 + y²/4 = 1

   (B) x²/4 + y²/3 = 1

   (C) 4x²/3 + 4y²/3 = 1

   (D) none of these

8. If any tangent to x²/a² + y²/b² = 1 intercepts lengths h and k on axes, then

   (A) h²/a² + k²/b² = 1

   (B) h²/a² + k²/b² = 2

   (C) a²/h² + b²/k² = 1

   (D) a²/h² + b²/k² = 2

9. Latus rectum of ellipse 4x²+9y²−8x−36y+4=0 is

   (A) 8/3

   (B) 4/3

   (C) 5/3

   (D) 16/3

10. The ellipse having vertices at (±5, 0) and foci at (±4, 0) has equation

    (A) x²/25+y²/16=1

    (B) 4x²+5y²=20

    (C) 9x²+25y²=25

    (D) none

11. x²/(10−a) + y²/(4−a) = 1 represents an ellipse if

    (A) a<4

    (B) a>4

    (C) 4<a<10

    (D) a>10

12. Tangents drawn at the ends of latus recta of x²/9 + y²/5 = 1 form a quadrilateral of area

    (A) 27

    (B) 13/2

    (C) 15/4

    (D) 45

13. If x²/a² + y²/b² = 1 and x²−y²=c² cut orthogonally, then

    (A) a²+b²=2c²

    (B) b²−a²=2c²

    (C) a²b²=2c²

    (D) a²−b²=2c²

14. The number of c such that y=4x+c is tangent to x²/4+y²=1 is

    (A) 0

    (B) 1

    (C) 2

    (D) infinite

15. If the major axis of an ellipse is thrice the minor axis, its eccentricity is

    (A) 1/3

    (B) 1/3

    (C) 1/2

    (D) 2√2/3

Assignment Answers

Q	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Ans	C	B	A	A	B	B	B	C	A	B	A	A	D	C	D