BASIC CONCEPTS
A number in the form z = x + iy is called complex number where i = √−1 and x = Re(z), y = Im(z).
A complex number can also be defined as an ordered pair (x, y) ≡ x + iy.
Equality of two Complex Number
Two complex numbers are equal if and only if their real and imaginary parts are separately equal i.e.
If z₁ = x₁ + i y₁, z₂ = x₂ + i y₂ be such that z₁ = z₂ ⇒ x₁ = x₂, and y₁ = y₂.
Algebra of Complex Numbers
(i) Addition: The sum of two complex numbers x₁ + i y₁ and x₂ + i y₂ is (x₁ + x₂) + i(y₁ + y₂).
(ii) Subtraction: The difference of two complex numbers x₁ + i y₁ and x₂ + i y₂ is (x₁ − x₂) + i(y₁ − y₂).
(iii) Multiplication: The product of two complex numbers x₁ + i y₁ and x₂ + i y₂ is (x₁x₂ − y₁y₂) + i(x₁y₂ + y₁x₂).
(iv) Division: If x₁ + i y₁ and x₂ + i y₂ be two complex numbers and x₂ + i y₂ ≠ 0, then
x₁ + i y₁/ x2 + i Y2 = (x₁ x₂ + y₁ y₂)/(x₂² + y₂²) + i[(x₂ y₁ − x₁ y₂)/(x₂² + y₂²)]
Conjugate of Complex Number
If z = x + iy, then its conjugate is given by ̄z = x - iy
Properties of conjugate
- ̄(̄z) = z
- z + ̄z = 2Re(z)
- z̄z = |z|2 = |̄z|2
- z1 - z2 = ̄z1 - ̄z2
- ̄zn = (̄z)n
- A complex number z is purely real iff ̄z = z.
- A complex number z is purely imaginary iff ̄z = -z.
- |z| = |̄z|
- z - ̄z = 2iIm(z)
- ̄(z1 + z2) = ̄z1 + ̄z2
- ̄(z1z2) = ̄z1̄z2
- ̄(&frac{z1}{z2}) = &frac;̄z1;̄z2
Modulus and Argument of a complex number
The modulus of complex number z = x + iy is denoted by |z| and given by |z| = √(x2 + y2), i.e., non-negative square root of x2 + y2.
The argument of complex number z = x + iy is value θ which satisfies the two equations.
cosθ = xx2 + y2,
sinθ = yx2 + y2
where θ = argz or amp(z)
Square root of a Complex Number
Let z1 = x1 + iy1 be the given complex number and we have to obtain its square root.
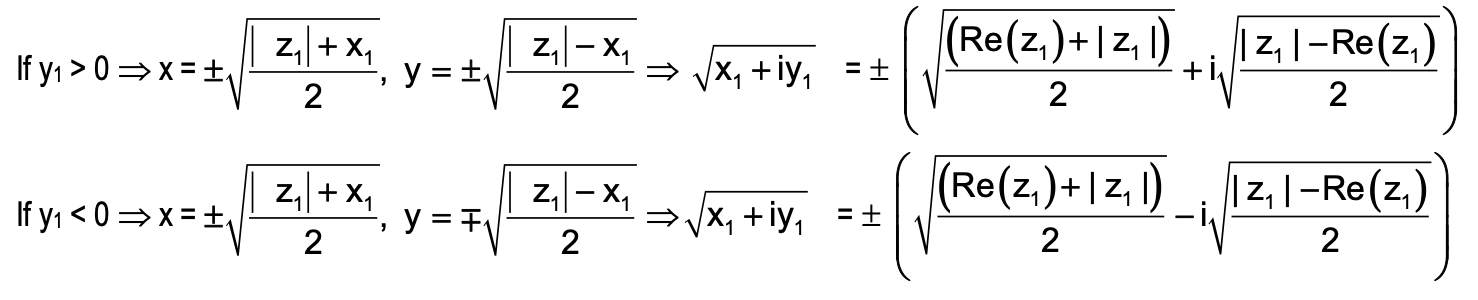
Unimodular complex number:- If |z| = 1 then the complex number z is called unimodular, therefore we can write z = cos q + i sin q and
Properties of argument
Argument of any complex number z lies in the interval -p < q £ p
(i) Arg z1z2 = arg z1 + arg z2
(ii) Arg (z1/z2) = arg z1 – arg z2
(iii) arg (zn) = n arg z. ", n Î I
(iv) arg z = 0 or p Þ z is purely real
(v) arg z = p/2 Þ z is purely imaginary
Equation of Straight Line Joining the Points z1 and z2
- General equation of a straight line is a&conj;z + &conj;a z + b = 0 , where a is a complex number and b is a real number.
- The length of the perpendicular from a point z1 to the line a&conj;z + &conj;a z + b = 0 is given by (a&conj;z1 + &conj;a z1 + b) / 2|a| .
Equation of a Circle
zzˉ+azˉ+aˉz+b=0,zzˉ+azˉ+aˉz+b=0,
where centre = –a and radius
=∣a∣2−b=∣a∣2−b
Example:
The centre and radius of the circle
zzˉ+(1−i)z+(1+i)zˉ−7=0iszzˉ+(1−i)z+(1+i)zˉ−7=0is
(A) –1 – i, 3
(B) 1 + i, 3
(C) 2 – i, 4
(D) 2 + i, 4
Solution:
(A). Given equation can be rewritten as
zzˉ+(1+i)zˉ+(1−i)z−7=0zzˉ+(1+i)zˉ+(1−i)z−7=0
So, it represents a circle with centre at –1 – i and
radius =
∣1+i∣2−(−7)=2+7=3∣1+i∣2−(−7)=2+7=3