Real Functions and Their Properties
A function f from a non-empty set A to a non-empty set B associates to each element x in A with a unique element in B which is denoted by f (x). The set A is called domain of the function f, the set B is called co-domain of f, f (x) is called value of the function f at x and the set {f (x): x ∈ A} is called range of f (or the image of A). f: A → B denotes the function f from A to B, in fact f (x) is the value of the function f at x. f (x) is also called the image of x under the function f.
Functions whose domain and co-domain both are subsets of R, the set of real numbers, are called real valued functions of a real variable i.e. a real function.
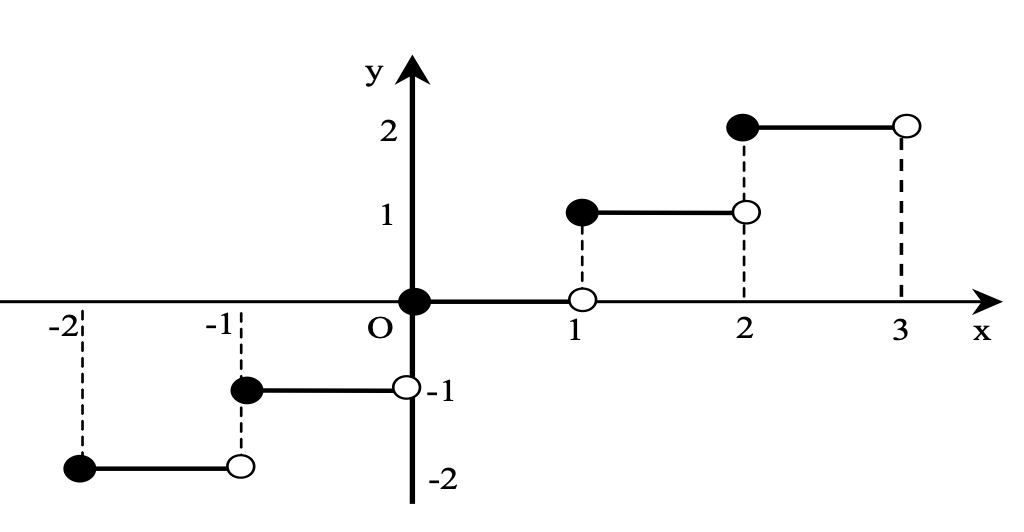
Greatest Integer Function (Step or Floor Function)
Let x ∈ ℝ be any real number. [x] denotes the greatest integer less than or equal to x. e.g. [3.01] = 3, [−3.99] = −4 etc.
Fractional Part
We have seen that x ≥ [x]. The difference between the number ‘x’ and its integral value ‘[x]’ is called the fractional part of x and is symbolically denoted as {x}.
Thus, {x} = x − [x]
e.g. if x = 4.92 then [x] = 4
and {x} = 0.92.
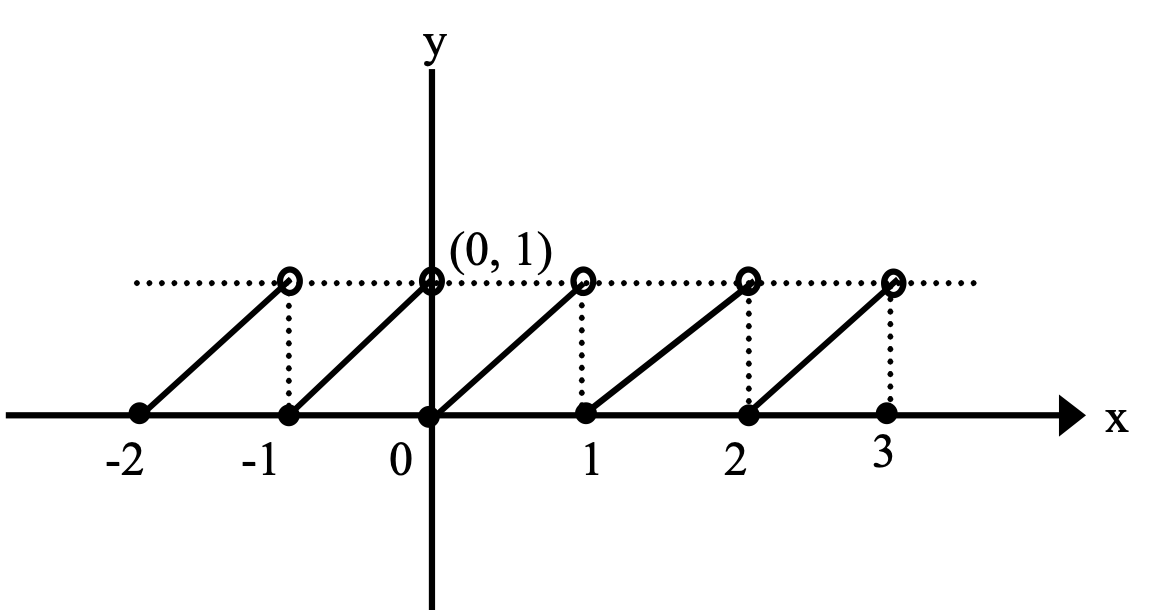
We can check that fractional part of any number is always non-negative and less than one.
If x is an integer ⇒ x = [x] ⇒ {x} = 0
⇒ {[x]} = 0
Exponential Function
If \( a \) is a positive real number, then the function defined by f(x) = ax, x ∈ R is called an exponential function to the base a.
Domain f = R; Range (f) = set of positive numbers.
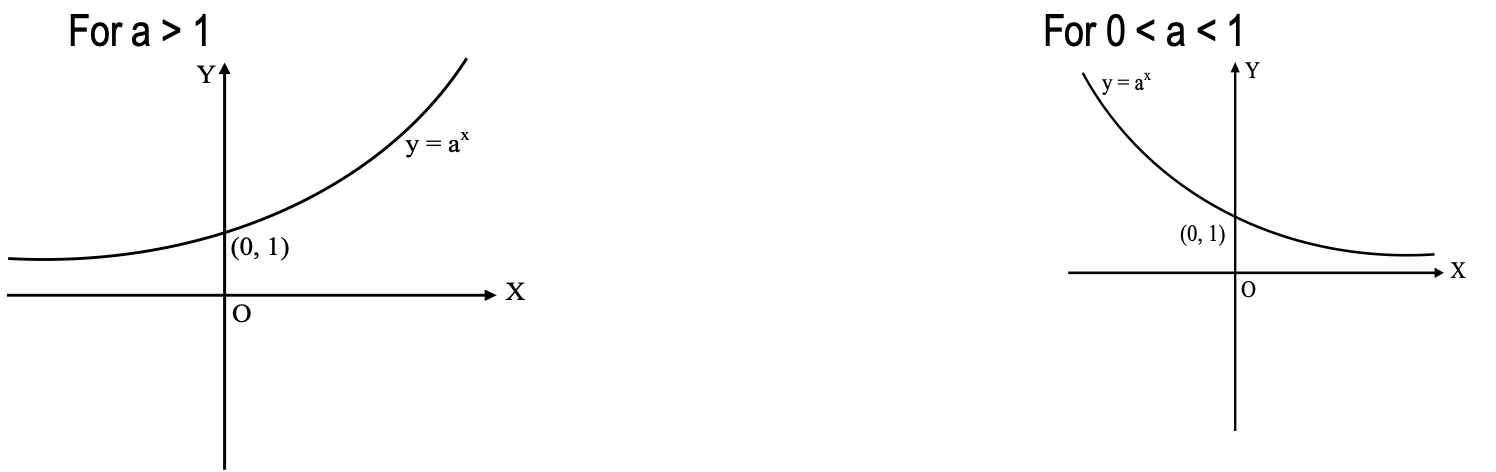
Observations
- a) The graph is above the x-axis.
- b) for a > 1, as we move from left to right, the graph rises above, and for 0 < a < 1, as we move from left to right the graph falls and it looks to touch the x-axis as we approaches to infinity.
If a = e, where e is an irrational number lying between 2 and 3, then the exponential function takes the form f (x) = ex, x ∈ R.
Domain (f) = R
Range (f) = the set of real positive numbers.
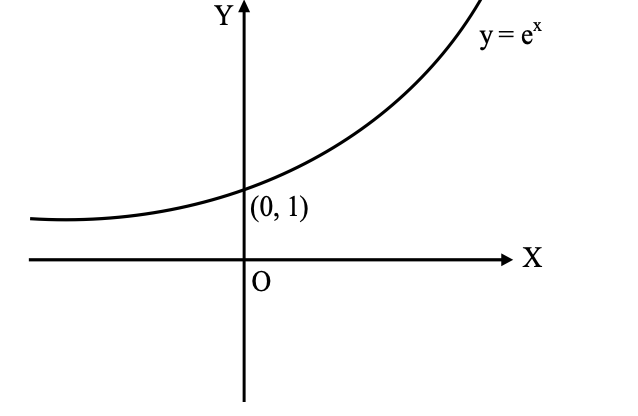
The curve is an increasing curve. It passes through (0, 1).
Note:
- For \( a > 1 \):
- If \( -\infty < x \leq 0 \), then \( 0 < f(x) \leq 1 \);
- If \( 0 < x < \infty \), then \( 1 < f(x) < \infty \)
- For \( 0 < a < 1 \):
- If \( 0 \leq x < \infty \), then \( 0 < f(x) \leq 1 \);
- If \( -\infty < x < 0 \), then \( 1 < f(x) < \infty \).
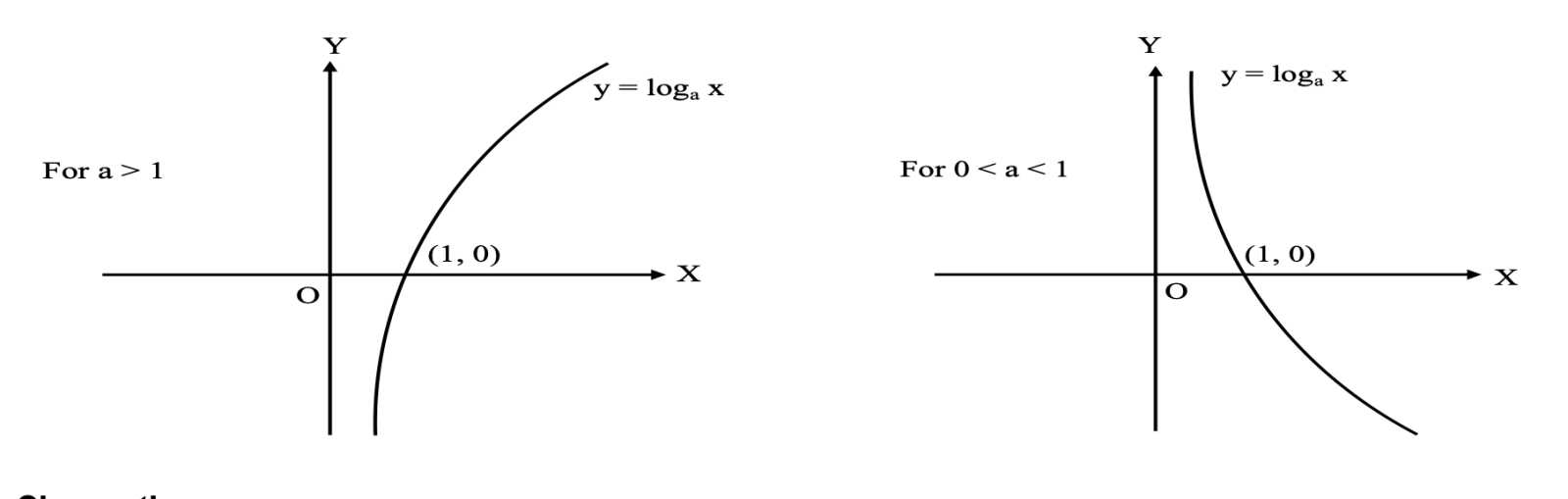
Logarithmic Function
Observations
Logarithmic Function
If a > 0 and a ≠ 1, then the function f : R+ → R f : R+→ R defined by y = loga xy = loga x iff ay= x is called the logarithmic function.
Domain (f) = R+; Range (f) = R
Observations
| 0 < a < 1 | a > 1 |
|---|---|
| • loga x is a decreasing function | • loga x is an increasing function |
| • limx→∞ loga x = −∞ | • limx→∞ loga x = ∞ |
| • limx→0 loga x = ∞ | • limx→0 loga x = −∞ |
| • sign of loga x is positive for 0 < x < 1 and sign of loga x is negative for x > 1 | • sign of loga x is negative for 0 < x < 1 and sign of loga x is positive for x > 1. |
An Important special case of logarithmic function as f (x) = loge x whose graph is
Domain (f) = R+ ; Range (f) = R.
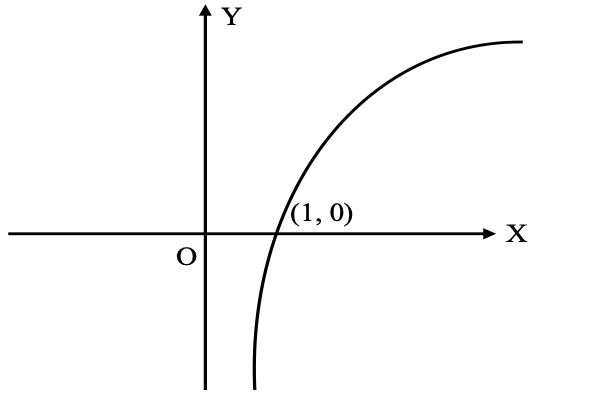
Observations
Curve is increasing and meets x-axis at (1, 0)
Note:
• logba1 ≥ logba2 ⇒ { a1 ≥ a2 > 0 if b > 1, 0 < a1 ≤ a2 if 0 < b < 1 }
Signum Function
The function f: ℜ → ℜ defined by
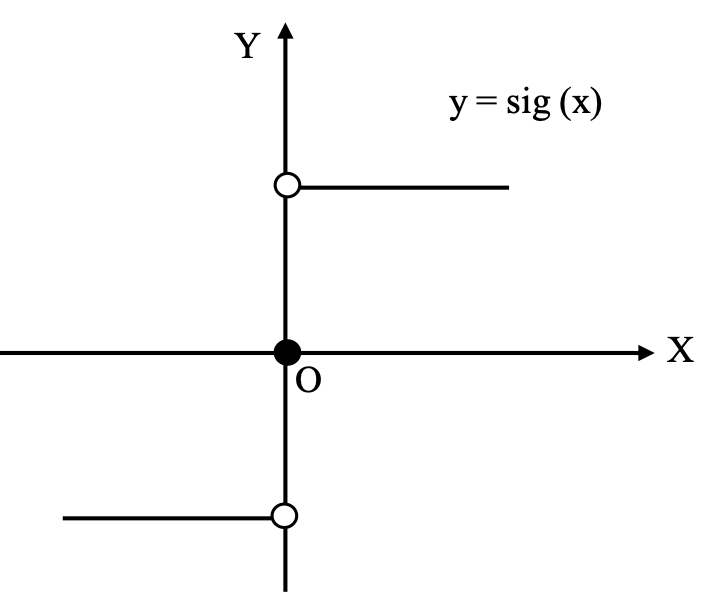
is called the signum function. The domain of the signum function is ℜ and the range is the set {−1, 0, 1}.
Note: The points (0, 1) and (0, –1) are not included in the graph where as the point (0, 0) is included.
Alternate ways the express signum function are

Even and Odd Function
If f : X → Y is a real valued function such that for all x ∈ D ⇒ – x ∈ D (where D is the domain of f) and if f (–x) = f (x) for all x ∈ D then f is said to be an even function and if f (–x) = – f (x), then f is said to be odd function. Even functions are symmetric about the y-axis and odd functions are symmetric about the origin.
Note:
- A function can be even or odd or neither.
- Every function defined in symmetric interval D(i.e. x∈D⇒−x∈Dx∈D⇒−x∈D) can be expressed as the sum of an even and an odd function.
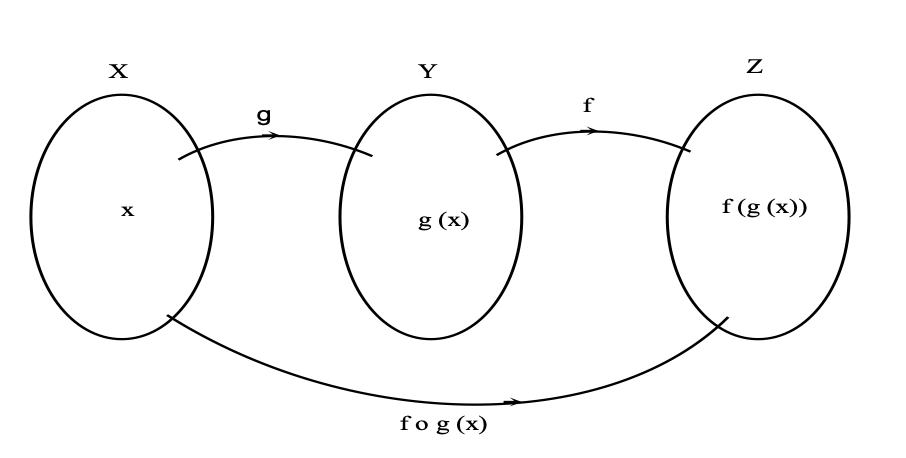
Composition of two Functions
Let f and g be any two real functions such that the domain of f includes the range of g. Then it makes sense to talk of f(g(x)) for each x in the domain X of g. Thus f(g(x)) is a unique element associated to x, (x ∈ X) in this way. As such it defines a function with domain X. We denote the function by f ∘ g and call it composite of f and g. If f : Y → Z and g : X → Y, then f ∘ g : X → Z is defined by the rule
(f ∘ g)(x) = f(g(x)), for all x ∈ X.
One-One Function (injective Function)
A function f : A → B is said to be one-one or injective function if different elements of set A have different f images in set B. Thus no two elements of set A can have the same f image. In other words f(x1) = f(x2) Þ x1 = x2.
e.g. f : R → R given by f (x) = 2x + 3 is one-one.
Many-One Function
A function f : A → B is called many one if at least one element in the set B is the f image of more than one elements of A.
e.g. f : R → R given by f (x) = x2 + 2 is many-one.
Methods to Determine One-One and Many-One
(i) Let x1, x2 ∈Domain of f and if x1 ≠ x2 ⇒ f(x1) ≠ f(x2) for every x1, x2 in the domain, then f is one-one else many-one.
(ii) Conversely if f(x1) = f(x2) ⇒ x1 = x2 for every x1, x2 in the domain, then f is one-one else many-one.
(iii) A function is one-one if and only if no line parallel to the x-axis meets the graph of the function at more than one point.
Onto or (surjective function)
The function f : A → B is said to be an onto function if every element of B is image of atleast one-element of A. i.e., for each y ∈ B, there exists atleast one x ∈ A such that f(x) = y, then f is an onto function. Range of f = co-domain of f(B)
Into function
If the function f : A → B is such that there is atleast one element of B which is not the image of any element of A, then f is called an into function.
Onto function is also called Surjective function and a function which is both one-one and onto is called Bijective function.
Range of f ⊂ co-domain of f.
e.g. f : R→R where f(x) = sinx is into.
f : R→R where f(x) = ax³ + b is onto where a ≠ 0, b ∈ R.
Note that a function will either be onto or into.
Methods to Determine Function Types
Methods to Determine whether a Function is Onto or Into
(i) If Range = codomain, then f is onto. If range is a proper subset of codomain, then f is into.
(ii) Solve f(x) = y for x, say x = g(y).
Now if g(y) is defined for each y ∈ codomain and g(y) ∈ domain of f for all y ∈ codomain, then f(x) is onto. If this requirement is not met by at least one value of y in codomain, then f(x) is into.
Remark:
An into function can be made onto by redefining the co-domain as the range of the original function.
Inverse Function
Let us consider a one-one onto function with domain A and range B. Let y ∈ B.
This member y ∈ B arises from one and only one member x ∈ A such that f(x) = y, as the function is one-one.
Thus we can define a new function say 'g' such that
g(y) = x ⟺ f(x) = y
we can also denote g by f-1.
In this case domain of f-1 = range of 'f'.
and range of f-1 = domain of 'f'.
Only one-one onto functions are invertible. All one-one onto functions are strictly monotonic in nature, hence sufficient condition for the existence of invertibility of an onto function y = f(x) is that it must be strictly monotonic. If a function increases or decreases then its inverse also increases or decreases accordingly.
Methods of Finding Inverse of a Function
(i) If you are asked to check whether the given function y = f(x) is invertible, you need to check that y = f(x) is one-one and onto.
(ii) If you are asked to find the inverse of a bijective function f(x), you do the following:
If f-1 be the inverse of f, then
f-1of(x) = fof-1(x) = x (always)
Apply the formula of f on f-1(x) and use the above identity to solve for f-1(x).
Formula and Concepts
Mathematical Function Definitions
1. A mapping f: X → Y is said to be a function if each element in the set X has its image in set Y. It is possible that a few elements in the set Y are present, which are not the images of any element in set X.
2. Every element in set X should have one and only one image. That means it is impossible to have more than one image for a specific element in set X. Functions can't be multi-valued (A mapping that is multi-valued is called a relation from X to Y).
3. Set 'X' is called domain of the function 'f'. Set 'Y' is called the co-domain of the function 'f'.
4. Set of images of different elements of set X is called the range of the function 'f'.
5. The function 'h' defined above is called the composition of f and g and is denoted by gof. Thus (gof)x = g(f(x)). Clearly Domain (gof) = {x : x ∈ Domain (f), f(x) ∈Domain(g)}
7. f(x) - f(-x) = 0 even function
8. f(x) + f(-x) = 0 odd function