Permutations and Combinations Solutions

Multiplication Principle

If one experiment has n possible outcomes and another experiment has m possible outcomes, then there are m ´ n possible outcomes when both of these experiments are performed.

Illustration 1: A college offers 7 courses in the morning and 5 in the evening. Then the possible number of choices with the student if he wants to study one course in the morning and one in the evening, is

(A) 25 (B) 35

(C) 20 (D) 36

Solution: The student has seven choices from the morning courses out of which he can select one course in 7 ways.

For the evening course, he has 5 choices out of which he can select one in 5 ways.

Hence the total number of ways in which he can make the choice of one course in the morning and one in the evening = 7 ´ 5 = 35.

Permutations (Arrangemnet of Objects)

The number of permutations of n objects, taken r at a time, is the total number of arrangements of r objects, selected from n objects where the order of the arrangement is important.

Without Repetition

(a) The number of arrangements of n different objects taken all at a time = ⁿp_n = n!

(b) The number of arrangements of n different objects taken r objects at a time = ⁿp_r =

With Repetition

The number of permutations (arrangements) of n different objects, taken r at a time, when each object may occur once, twice, thrice…. upto r times in any arrangement= (n)^r

Illustration 2: The number of 3 digit numbers can be formed using the digits 0, 1,2,3,4,5 so that digits may not be repeated is

(A) 100 (B) 200

(C) 150 (D) 50

Solution: (A). Let the 3-digit number be XYZ

Position (X) can be filled by 1,2,3,4,5 but not 0. So it can be filled in 5 ways.

Position (Y) can be filled in 5 ways again. (Since 0 can be placed in this postion).

Position (Z) can be filled in 4 ways. Hence, by the fundamental principle of counting, total number of ways is 5 x 5 x 4 = 100 ways.

Exercise 1:

 1. The number of ways 5 distinct red balls and 5 identical white balls can be arranged in a row so that neither any two red balls nor any two white balls come together

(A) 260

(B) 240

(C) 200

(D) none of these

2. The number of ways in which four girls and seven boys sit in a row so that no two girls sit together

(A) ⁸P₄ . 7!

(B) 936

(C) 24

(D) none of these

3. If the number of permutations of at most two objects out of n distinct objects is 16, then value of n is

(A) 2

(B) 3

(C) 4

(D) 5

Circular Permutations

The arrangements we have considered so far were linear. There are arrangements in closed loops also, called as circular arrangements.

The total number of circular arrangements of n persons is = (n – 1)!.

Example: The number of ways in which 10 boys and 5 girls can sit around a circular table so that no two girls sit together is

Solution: (A). 10 boys can be seated in a circle in 9! ways. There are 10 spaces inbetween the boys, which can be occupied by 5 girls in ¹⁰p₅ ways. Hence total number of ways

= 9! ¹⁰p₅ =.

Combinations

Meaning of combination is selection of objects.

Selection of Objects without Repetition

The number of selections (combinations or groups) that can be formed from n different objects taken r (0 £ r £ n) at a time is 

Selection of objects with repetition

The number of combinations of n distinct objects, taken r at a time when each may occur once, twice, thrice,….. upto r times in any combination is ⁿH_r = ^n+r-1C_r .

Example: Let 15 toys be distributed among 3 children subject to the condition that any child can take any number of toys. Then the required number of ways to do this if toys are distinct

(A) 3¹⁵

(B) ¹⁷C₂

(C) 15³

(D) 3¹⁵ - 1

Solution: (A). Toys are distinct

Here we have 3 children and we want the 15 toys to be distributed to the 3 children with repetition. In other words, it is same as selecting and arranging children 15 times out of 3 children with the condition that any child can be selected any no. of time, which can be done in 3¹⁵ ways (n = 3, r = 15).

Restricted Selections/ Arrangements

(a) The number of ways in which r objects can be selected from n different objects if k particular objects are

• always included = ^n-k C_r-k
• never included = ^n-k C_r

(b) The number of arrangements of n distinct objects taken r at a time so that k particular objects are

• always included = ^n-k C_r-k .r!

(ii) never included = ^n-k C_r .r!

Some Results Related to ⁿC_r

(i) ⁿC_r = ⁿC_n-r

• If ⁿC_r = ⁿC_k , then r = k or n-r =k
• ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r
• ⁿC_r = ^n-1C_r-1

(v)  

(vi) (a) If n is even , ⁿC_r  is greatest for r = n/2

       (b) If n is odd, ⁿC_r  is greatest for r = ,

Exercise 2:

1. The number of ways in which four letters can be selected from ‘FIITJEE’

(A) 18

(B) 20

(C) 25

(D) 28

2. The number of ways in which a committee of 5 persons be formed out of 6 men and 4 women when atleast one woman has to be necessarily selected

(A) 200

(B) 250

(C) 246

(D) none of these

Selection from Distinct Objects:

The number of selections from n different objects, taken at least one

= ⁿC₁ + ⁿC₂+ ⁿC₃+------ + ⁿC_n = 2ⁿ-1.

Selection from Identical Objects

• The number of selections of r objects out of n identical objects is 1.
• Total number of selections of zero or more objects from n identical objects is n+1.
• The total number of selections of at least one out of a₁+a₂+a₃+----+a_n objects, where a₁ are alike (of one kind ), a₂ are alike (of second kind ) and so on ---------a_n are alike (of nth kind ), is [(a₁+1)(a₂+1)(a₃+1)-------(a_n+1)]-1.

Ex.: Let a person have 3 coins of 25 paise, 4 coins of 50 paise and 2 coins of 1 rupee. Then, number of ways in which can he give none or some coins to a beggar

(A) 20

(B) 60

(C) 35

(D) 36

Solution: (B). Total number of ways of giving none or some coins is
( 3 +1 )( 4+1)(2+1) = 60 ways.

Total Number of Divisors of a given Natural Number

To find number of divisors of a given natural number greater than 1 we can write n as

n = 

where p₁, p₂, ... ,p_n are distinct prime numbers and a₁, a₂,...a_n are positive  integers.

Sum of All the Divisors of n is given by

Ex.: If n = 10800, then the total number of divisors of n

(A) 60

(B) 34

(C) 24

(D) 84

Solution: (A). n = 10800 = 2⁴ ´ 3³´ 5²

Any divisor of n will be of the form 2^a ´ 3^b ´ 5^c 

where 0 £ a £ 4, 0 £ b £ 3, 0 £ c £ 2 . For any distinct choices of a,b and c , we get a divisor of n

Total number of divisors = ( 4+1)( 3+1) ( 2+1) = 60

Division and Distributions of Objects

(with fixed number of objects in each group)

Into groups of unequal size (different number of objects in each group):

(a) Number of ways in which n distinct objects can be divided into r unequal groups containing a₁ objects in the first group, a₂ objects in the second group and so on

= 

(b) Number of ways in which n distinct objects can be distributed among r persons such that first person gets a₁ objects, 2^nd person gets a₂ objects …., r^th person gets a_r objects

= 

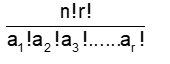
Into groups of equal size (each group containing same number of objects)

• Number of ways in which m´n distinct objects can be divided equally into n groups (unmarked) = 
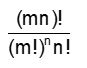
• Number of ways in which m´ n different objects can be distributed equally among n persons (or numbered groups) = (number of ways of dividing into groups)´(number of groups)! = 

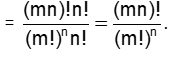
Derangement

Let S = { 1, 2,3, . . . ,n} , then a function f from S to S known as derangement if f is a bijective function and f(i) ¹ i for any i Î S.

In other words rearrangement of objects such that no one goes to its original place is called derangement

If 'n' things are arranged in a row, the number of ways in which they can be deranged so that none of them occupies its original place is

= 

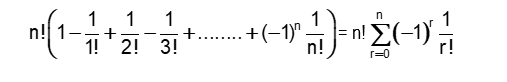
and it is denoted by D(n)

Example: Suppose 4 letters are taken out of 4 different envelopes. Then number of ways in which they be reinserted in the envelopes so that no letter goes in to its original envelope

(A) 9

(B) 10

(C) 8

(D) 14

Solution: (A). Using the formula for the number of derangements that are possible out of 4 letters in 4 envelopes, we get the number of ways as :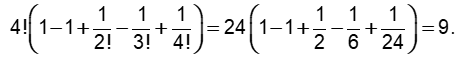 

Exercise 3:

1. The number of ways in which 10 person make 5 pairs and dance iIn the same hall

(A) 10!

(B) 

(C)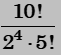

(D) none of these

2. The number of ways in which 3 women and their husbands dance so that no woman dances with her own husband

(A) 1

(B) 2

(C) 3

(D) 4

Answer to Exercises

Exercise 1. (i) B

(ii) A

(iii) C

Exercise 2. (i) C

(ii) A

Exercise 3. (i) B

(ii) B

Formulae and Concepts at a Glance

1. Without Repetition: arranging n objects, taken r at a time is equivalent to filling r places from n things is= 
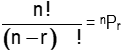
2. The number of arrangements of n different objects taken all at a time = ⁿp_n = n!
3. With Repetition: The number of permutations (arrangements) of n different objects, taken r at a time, when each object may occur once, twice, thrice …. upto r times in any arrangement = (n)^r
4. The number of arrangements that can be formed using n objects out of which p are identical (and of one kind), q are identical (and of another kind), r are identical (and of another kind) and the rest are distinct is. 

5. The total number of circular arrangements of n persons is = 
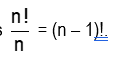
6. If no distinction is made between the clockwise and the anti-clockwise arrangements of n different objects around a circle, then the number of arrangements is (n – 1)!
7. The number of selections (combinations or groups) that can be formed from n different objects taken r (0 £ r £ n) at a time is.
8. The number of ways in which r objects can be selected from n different objects if k particular i) objects are always included = ^n-k C_r-k ii) never included = ^n-k C_r
9.  The number of arrangements of n distinct objects taken r at a time so that k particular objects are iii) always included = ^n-k C_r-k .r! iv) never included = ^n-k C_r .r!
10. The number of selections from n different objects, taken at least one = ⁿC₁ + ⁿC₂ + ⁿC₃ + … + ⁿC_n = 2ⁿ – 1.
11. The number of ways in which m´n distinct objects can be divided equally into n groups (unmarked) = 
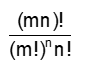
12. The number of ways in which m´ n different objects can be distributed equally among n persons (or numbered groups) = (number of ways of dividing into groups) ´ (number of groups)! = 

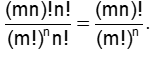
Solved Examples

1. Number of ways in which four letter of the word ‘DEGREE’ can be selected is 

   (A) 7 (B) 6

   (C) 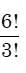 (D) none of these.

   Sol. (A). In DEGREE we have three E’s and D, G, R

   Four letters can be selected in following ways

   (i) Three alike, one different letter ³C₁ ´ ³C₃ (ii) Two alike, two different letter ³C₂

   (iii) all different letter ³C₃ Total number of ways = ³C₁ + ³C₂ + ³C₃ = 7.

   2. The number of ways in which a mixed double game can be arranged amongst 9 married couples if no husband and wife play in the same game is

   (A) 756 (B) 1512

   (C) 30 24 (D) none of these.

   Sol. (B). We can choose two men out of 9 in ⁹C₂ ways. Since no husband and wife are to play in the same game, two women out of the remaining 7 can be chosen in ⁷C₂ ways. If M₁, M₂ , W₁ and W₂ are chosen, then a team may consist of M₁ and W₁ or M₁ and W₂. Thus the number of ways of arranging the game is

   ( ⁹C₂)( ⁷C₂)(2) = = 1512.

   3. The number of ways of selecting 10 balls out of an unlimited number of white, red, blue and green balls is

   (A) 270 (B) 84

   (C) 286 (D) 86

   Sol. (C). Let x_{1 ,}x₂ , x₃, x₄ be the number of white, red, blue, green balls respectively that are selected. Then x₁ +x₂+ x₃+x₄ = 10. The required of ways = coefficient of y¹⁰ in

   ( 1+ y+ y² + y³ + . . . )⁴ = coefficient of y¹⁰ in(1 - y)^-4

   = coefficient of y¹⁰ in ( 1+ ⁴C₁ y + ⁵C₂y² +⁶C₃y³ + . .=.

   4. The number of times of the digits 3 will be written when listing the integer from 1 to 1000 is

   (A) 269 (B) 300

   (B) 271 (D) 302

   Sol. (B). Since 3 does not occur in 1000, we have to count the number of times 3 occurs when we list the integers from 1 to 999. Any number between 1 and 999 is of the form xyz where 0 £ x, y, z£ 9 . Let us first count the numbers in which 3 occurs exactly once. Since 3 can occur at one place in ³C₁ ways, there are ³C₁ ( 9´9) = 3´ 9² such numbers. Next, 3 can occur exactly two places in (³C₂) (9) = 3 ´ 9 such numbers. 

   Lastly , 3 can occur in all three digits in one number only. Hence the number of times 3 occurs is 1 ´ ( 3´ 9²) + 2´ ( 3´9) + 3´1 = 300

   5. Five balls of different colours are to be placed in three boxes of different sizes. Each box can hold all five balls. The number of ways in which we can place the balls in the boxes (order is not considered in the box) so that no box remains empty is

   (A) 150 (B) 300

   (C) 200 (D) none of these

   Sol. (A). One possible arrangement is 

   Three such arrangements are possible. Therefore, the number of ways is ( ⁵C₂) ( ³C₂) ( ¹C₁) (3) = 90

   The other possible arrangements 

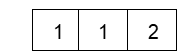
   Three such arrangements are possible. In this case, the number of ways is ( ⁵C₁) ( ⁴C₁) ( ³C₃) (3) = 60

   Hence, the total number of ways is 90 + 60 = 150.

   6. A teacher takes 3 children from her class to the zoo at a time as often as she can, but she does not take the same three children to the zoo more than once. She finds that she goes to the zoo 84 times more than a particular child goes to the zoo. The number of children in her class is

   (A) 12 (B) 10

   (C) 60 (D) none of these .

   Sol. (B). The number of times the teacher goes to the zoo = ⁿC₃.

   The number of times a particular child goes to the zoo = ^n-1C₂.

   From the question, ⁿC₃ – ^n-1C₂ = 84.

   Or (n - 1)(n –2)(n –3) = 6 ´ 84 = 9´ 8 ´ 7

   Þ n – 1 = 9 Þ n = 10 .

   7. There are three coplanar parallel lines. If any p points are taken on each of the lines, the maximum number of triangles with vertices at these points is

   (A) 3p²( p-1) +1 (B) 3p²( p-1)

   (C) p²( 4p –3) (D) none of these

   Sol. (C). The number of triangles with vertices on different lines = ^pC₁ ´ ^PC₁ ´^pC₁ = p³ .

   The number of triangles with two vertices on one line and the third vertex on any one of the other two lines

   = ³C₁{ ^pC₂ ´^2pC₁} = 6p. 

   so, the required number of triangles = p³ + 3p²(p -1) = p²( 4p – 3)

   8. Two teams are to play a series of 5 matches between them. A match ends in a win or loss or draw for a team. A number of people forecast the result of each match and no two people make the same forecast for the series of matches. The smallest group of people in which one person forecasts correctly for all the matches will contain n people, where n is

   (A) 81 (B) 243

   (C) 486 (D) none of these

   Sol. (B). The smallest number of people = total number of possible forecasts

   = total number of possible results = 3´ 3 ´ 3´3 ´3 = 243.

   9. In a plane there are two families of lines y = x +r, y = -x +r , where r Î { 0, 1, 2, 3, 4} . The number of squares of diagonals of length 2 formed by the lines is

   (A) 9 (B) 16

   (C) 25 (D) none of these

   Sol. (A). There are two sets of five parallel lines at equal distances. Clearly, lines like l₁, l₃, m₁, m₃ form a squares whose diagonal’s length is 2 

   So, the number of required squares = 3´ 3 

   {since choices are (l₁, l₃),
   (l₂, l₄), (l₃, l₅) for one set, etc)

   10. Let and be a variable vector such that are positive integers. If £ 12, then the number of values of is

   (A) ¹²C₉ –1 (B) ¹²C₃

   (C) ¹²C₉ (D) none of these

   Sol. (B). If then from the question x, y, z are positive integers.

   Also £ 12 Þ x +y + z £ 12.

   So, the number of values of

   = the number of positive integral solutions of ( x+y+z £ 12)

   = ²C₂ +³C₂ + . . . + ¹¹C₂

   = ³C₀ + ³C₁ +⁴C₂+ . . . + ¹¹C₉ ( since ⁿC_r = ⁿC_n-r) =⁴C₁ + ⁴C₂ + ... +¹¹C₉ = ... = ¹²C₉