DEFINITION OF LIMIT
Let f(x) be a function of x. If for every positive number ε, however small it may be, there exists a positive number δ, such that whenever 0 < |x - a| < δ, we have f(x) - l| <ε, then we say ‘f(x) tends to the limit l as x tends to a’, and we write:
Lim (x → a) f(x) I.
Meaning of (x → a)
Let x be a variable and ‘a’ be a constant. x assumes values nearer and nearer to ‘a’, then we say ‘x tends to a’ and write ‘x → a’ and it doesn’t mean x = a.
Condition for Existence of Limit: Left and Right Limit
Let y = f(x) be a given function, and x = a is the point under consideration. Left tendency of f(x) at x = a is called its left limit and right tendency is called its right limit.
Left tendency (left limit) is denoted by f(a − 0) or f(a–) and right tendency (right limit) is denoted by f(a + 0) or f(a+) and are written as:
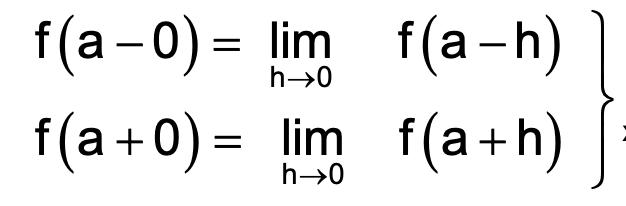
where ‘h’ is a small positive number.
Thus for the existence of the limit of f(x) at x = a, it is necessary and sufficient that f(a - 0) = f(a + 0), if these are finite or f(a - 0) and f(a + 0) both should be either + ∞ or − ∞.
Frequently Used Limits

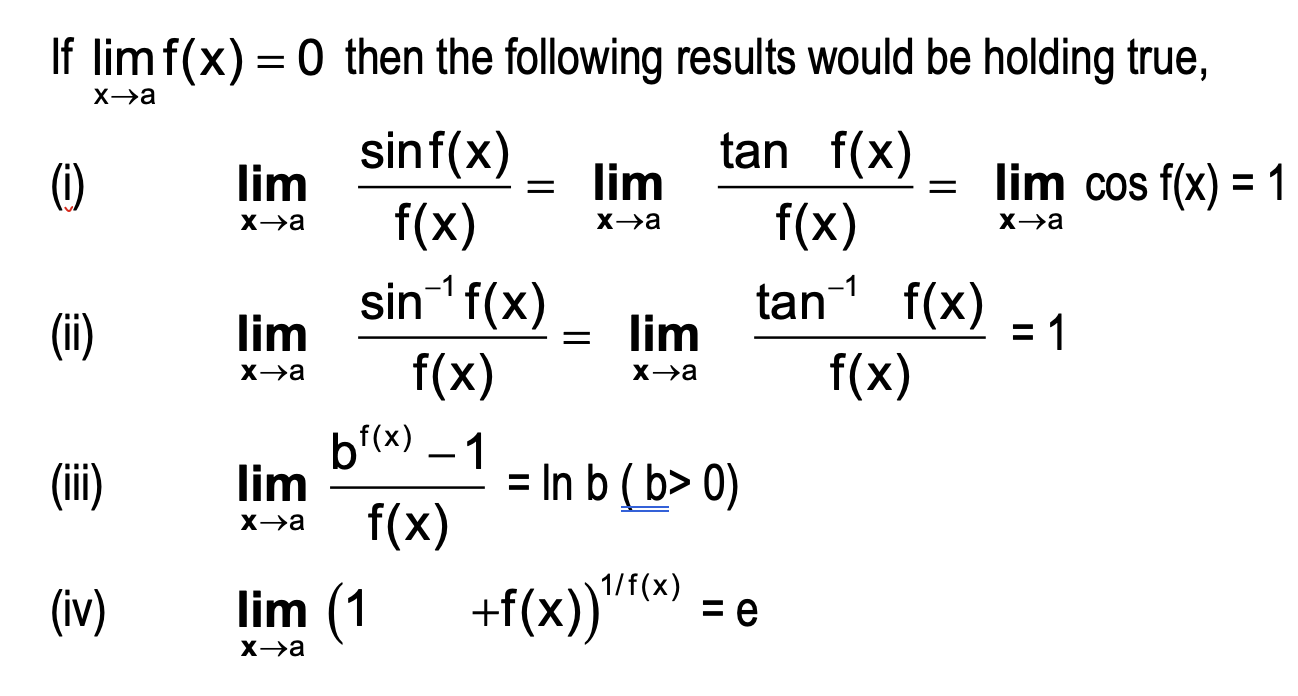
Evaluation of Limits (Working Rules)
- By factorization: To evaluate limx→aφ(x)/ψ(x), factorise both φ(x) and ψ(x), if possible, then cancel the common factor involving ‘a’ from the numerator and the denominator. In the last, obtain the limit by substituting ‘x’ for ‘a’.
- By Substitution: To evaluate limx→a f(x), put x = a + h and simplify the numerator and denominator, then cancel the common factor involving h in the numerator and denominator. In the last obtain the limit by substituting h = 0.
- By L–Hospital’s Rule: Apply L–Hospital’s rule to the form 0/0 or ∞/∞.
- By Rationalisation: In case if numerator or denominator (or both) are irrational functions, rationalisation of numerator or denominator (or both) helps to obtain the limits of the function.
- In case of limits x → ∞, put x = 1/t or t = 1/x, so that t → 0 when x → ∞ and proceed as usual.
- To find the limit by finding L.H.L and R.H.L.: We evaluate the limit of a function f(x) at x → a by finding its right hand limit (R.H.L) and left hand limit (L.H.L) in the special case when the values of f(x) are given by different functions of x for x < a and for x ≥ a.
Here we discuss two different cases,
(a) When limx→a f(x) = 1:
In this case,
limx→a [f(x)]g(x) = limx→a [1 + f(x) - 1]g(x)
= limx→a ( [1 + f(x) - 1]1/(f(x)-1) )g(x)(f(x)-1)
= elimx→a g(x)(f(x)-1)
because, limx→a ( [1 + f(x) - 1]1/(f(x)-1) ) = e
(b) When limx→a f(x) ≠ 1 but f(x) is positive in the neighbourhood of x = a.
In this case we write,
(f(x))g(x) = eg(x)·ln(f(x))
⇒ limx→a [f(x)]g(x) = elimx→a g(x)·ln(f(x))
Remark:
- If f(x) is not throughout positive in the neighbourhood of x = a, then limx→a (f(x))g(x) will not exist. Because in this case function will not be defined in the neighbourhood of x = a.
L'Hospital’s Rule
Let f(x) and g(x) be two functions differentiable in the neighbourhood of the point a, except at the point ‘a’ itself. If limx→a f(x) = limx→a g(x) = 0. Or, limx→a f(x) = limx→a g(x) = ∞. Then limx→a [f(x)/g(x)] = limx→a [f'(x)/g'(x)] provided that the limit on the right exist as a finite number or is ±∞.
- L’Hospitals rule is not always useful. Consider the example, limx → ∞ (x + sin x) / (x - sin x) (form ∞/∞).
Here, if we apply L’Hospital’s rule, then limx → ∞ (x + sin x) / (x - sin x) = limx → ∞ (1 + cos x) / (1 - cos x) .
Now, both the numerator and denominator are undefined because limx → ∞ cos x doesn’t exist.
We can find this limit as follows:
limx → ∞ (x + sin x) / (x - sin x) = limx → ∞ (1 + (sin x / x)) / (1 - (sin x / x)) = (1 + 0) / (1 - 0) = 1 since limx → ∞ (sin x / x) = 0 .
Use of Sandwich Theorem in Solving Problems
Sandwich theorem helps in calculating the limits, when limits can not be calculated using the usual methods. The following illustration would make the procedure clear,
CONTINUITY OF A FUNCTION
A function f(x) is said to be continuous at x = a if
limx→a- f(x) = limx→a+ f(x) = f(a)
If f(x) is not continuous at x = a, we say that f(x) is discontinuous at x = a.
f(x) will be discontinuous at x = a in any of the following cases:
(i) limx→a- f(x) and limx→a+ f(x) exist but are not equal.
(ii) limx→a- f(x) and limx→a+ f(x) exist and are equal but not equal to f(a).
(iii) f(a) is not defined.
(iv) At least one of the limits does not exist.

DIFFERENTIABILITY
Let y = f(x) be continuous in (a, b). Then the derivative or differential of f(x) at x ∈ (a, b), denoted by dy/dx or f′(x), and is defined as
provided the limit exists and is finite.
Right hand derivative
Right hand derivative of f(x) at x = a is denoted by, Rf′(a) or f′(a+) and defined as
Left hand derivative
Left hand derivative of f(x) at x = a is denoted by Lf′(a) or f′(a−) and is defined as
Clearly, f(x) is differentiable at x = a if and only if Rf′(a) = Lf′(a).
Note:
If a function f(x) is differentiable at x = a then it is also continuous at x = a. But if a function is continuous at a point, it is not necessarily differentiable at that point.
Formulas and Concepts
- For the existence of the limit at x = a, f(x) need not be defined at x = a. However if f(a) exists, limit need not exist or even if it exists then it need not be equal to f(a). limx→a f(g(x)) = f(limx→a g(x)) = f(ℓ2) , if and only if f(x) is continuous at x = ℓ2.
- Right hand derivative of f(x) at x = a is denoted by, Rf'(a) or f'(a+) and is defined as
R f'(a) = limh→0 [f(a+h) – f(a)] / h, h > 0.
- Left hand derivative of f(x) at x = a is denoted by Lf'(a) or f'(a–) and is defined as
L f'(a) = limh→0 [f(a–h) – f(a)] / –h, h > 0.
- f(x) is differentiable at x = a if and only if R f'(a) = L f'(a).
- L' Hospital's Rule
We have dealt with problems which had indeterminate form either 0/0 or ∞/∞.
The other indeterminate forms are ∞ − ∞, 0·∞, 00, ∞0, 1∞.
We state below a rule, called L' Hospital's Rule, meant for problems on limit of the form 0/0 or ∞/∞.
Let f(x) and g(x) be functions differentiable in the neighbourhood of the point a, except may be at the point a itself. If
limx→a f(x) = 0 = limx→a g(x)
or,
limx→a f(x) = ∞ = limx→a g(x),
then
limx→af(x)/g(x) = limx→af'(x)/g'(x)
provided that the limit on the right either exists as a finite number or is ±∞.
- If limx → a f(x) = 0, then the following results will be holding true:
- limx → a ¼sin f(x)⁄f(x)¾ = limx → a ¼tan f(x)⁄f(x)¾ = limx → a cos f(x) = 1
- limx → a ¼sin−1 f(x)⁄f(x)¾ = limx → a ¼tan−1 f(x)⁄f(x)¾ = 1
- limx → a ¼bf(x) - 1⁄f(x)¾ = ln b (b > 0)
- limx → a (1 + f(x))1/f(x) = e
SOLVED EXAMPLES
1. 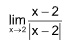 equals
equals
(A) 2 (B) 0
(C) –2 (D) none of these
Sol. (D). 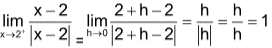 .
.
.png)
LHL ≠ RHL
Limit does not exist.
2. In order that the function f(x) = (x +1)cotx is continuous at x = 0, f(0) must be defined as
(A) f(0) = 0 (B) f(0) = e
(C) f(0) = 1/ e (D) none of these
Sol. (B). For continuity actual value must be equal to limiting value
A = limx→0(x+1)cotx
logA = limx→0cotxlog(x+1)
= limx→0log(x+1)/tanx [0/0 form]
= 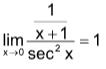 (By L’ Hospital Rule)
(By L’ Hospital Rule)
log A = 1 ⇒ A = e1 = e .
For f(0) must be defined as f(0) = e .
3. If f(x) = 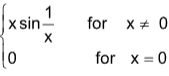 . Then
. Then
(A) f is not a continuous function
(B) f' (0+) exists but f' (0–) does not exist
(C) f' (0+) = f' (0–)
(D) f' (0+) and f' (0–) does not exist
Sol. (D). We have limx→0f(x)= limx→0xsin1/x = 0 = f(0) So, f is continuous at x = 0.
Therefore, f is a continuous function. As for the derivative f’(0) we have.
f' (0+) =  = which doesn’t exist
= which doesn’t exist
Similarly, the limit f' (0–) doesn’t exist.
4. 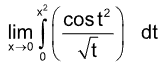 is equal to
is equal to
(A) 2 (B) 3
(C) 4 (D) 5
Sol. (A). 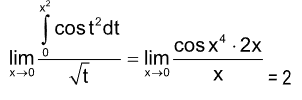 = 2
= 2
5. If f (x) = cos{π/2[x]-x3}, 1 < x < 2 (where [.] denotes the greatest integer function) then its derivative at x = (π/2)1/3 is equal to
(A) 0 (B) 3(π/2)2/3
(C) –3(π/2)3/2 (D) none of these
Sol. (A). x = ((π/2)1/3 ⇒ [x] = 1 ; So, f (x) = cos(π/2-x3)= sin x3; f'(x) = 3x2 cos x3
f'((π/2)1/3)= 3(π/3)2/3 cosπ/2 = 0
6. If f (9) = 9, f' (9) = 4, then 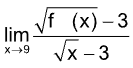 is equal to
is equal to
(A) 9 (B) 4
(C) 3 (D) 2
Sol. (B). f (9) = 9, f' (9) = 4
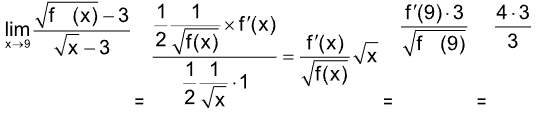
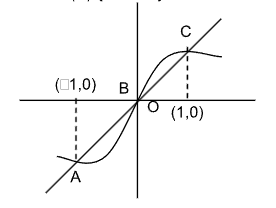
7. Let f : R ⟶ R be a function defined by f(x) = max{x, x3}. The set of all points where f(x) is NOT differentiable is
(A) {–1, 1} (B) {–1, 0)
(C) {0, 1} (D) {–1, 0, 1}
Sol. (D). f (x) = max (x, x3)
y = x, y = x3
x3 = x
x = 0, x = 1, – 1
from figure, it is very clear that
x is not differentiable at x = 0, – 1, 1
8. If f(x) =(x2+5x+3/x2+x+2)x, then limx→∞f(x) is
(A) e4 (B) e3
(C) e2 (D) 24
Sol. (A). .png) = e4.
= e4.
9. If 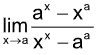 = –1, then
= –1, then
(A) a = 1 (B) a = 0
(C) a = e (D) none of these
Sol. (A). Applying L’Hospital rule
axIna - axa-1/xx(1+In x)=-1 ⇒ ln a – 1 = –(1 + ln a) ⇒ ln a = 0 ⇒ a = 1.
10. The value of limx→0(cosx + asinbx)1/x is
(A) 1 (B) ab
(C) eab (D) eb/a
Sol. (C). = 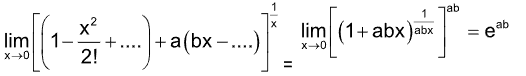
Frequently Asked Questions
A limit describes the value a function approaches as the input gets close to a number, even if it never reaches it. For example, as x approaches infinity in 1/x, the output approaches zero. A derivative measures the rate of change or slope of a curve at a specific point. Think of it like a speedometer: while distance shows where you are, the derivative shows how fast you’re moving at an instant. Derivatives are formally defined using limits, making limits the building block of calculus. Together, they form the foundation for understanding continuity, instantaneous change, and problem-solving in mathematics, physics, and economics.
A limit focuses on what value a function tends toward as inputs approach a point, while a derivative uses limits to measure instantaneous rates of change. In simple terms, limits deal with “approaching values,” while derivatives deal with “slopes” and “changes.” Every derivative depends on a limit, but not every limit defines a derivative. For instance, limits can describe behavior at infinity or discontinuities, while derivatives specifically measure the steepness of a curve. This distinction makes limits more general, while derivatives are a powerful application of limits in calculus.
The word “limit” comes from the idea of boundaries or approaching edges. In calculus, it represents the value a function approaches but might never reach. For example, approaching zero in 1/x or getting infinitely close to a wall without touching it illustrates the meaning. The concept formalizes how we handle infinite processes, discontinuities, or undefined values in a precise way. Calling it a “limit” emphasizes the importance of analyzing approach behavior rather than just evaluating at a point. This naming helps students intuitively grasp the boundary-like role of limits in defining continuity, derivatives, and integrals.
Derivatives are defined through the difference quotient limit:
This formula calculates the slope of the tangent line to a curve at a point. To use it, substitute the function into the formula, simplify the algebra, and take the limit as h approaches zero. For example, for f(x) = x2, the derivative is 2x. Although rules like the power rule or product rule simplify differentiation, their foundation comes directly from this limit definition. Practicing with this method strengthens conceptual understanding of derivatives as instantaneous rates of change.
The connection lies in the definition: a derivative is the limit of the difference quotient. Without limits, derivatives cannot exist. Limits ensure that we can measure instantaneous change even at infinitely small intervals. They also help analyze continuity, which is a prerequisite for differentiability. Essentially, limits provide the mathematical rigor to define how functions behave “close to” a point, and derivatives extend this idea to describe exact rates of change at that point. This relationship makes limits and derivatives inseparable concepts in calculus.
Limits form the foundation for both derivatives and integrals. A derivative is defined as a limit of difference quotients, while an integral is defined as the limit of Riemann sums (adding infinitely small areas under a curve). Together, derivatives and integrals are connected by the Fundamental Theorem of Calculus, which states they are inverse processes. For students, this means limits allow us to define change (derivatives) and accumulation (integrals) in precise terms. Understanding their unity helps link motion, area, and optimization problems across mathematics, physics, and economics.
Limits are vital in handling scenarios where direct evaluation isn’t possible. For example, in physics, they help analyze motion as time approaches zero, such as calculating instantaneous velocity. In engineering, limits are used to study stresses and load behaviors. In computer science, they appear in algorithms and numerical methods for approximations.
Even in daily life, such as predicting compound interest growth or analyzing population trends, limits are applied. Their usefulness comes from simplifying complex “approaching” behaviors into understandable results.
In physics, derivatives measure velocity and acceleration — key to understanding motion. They also model rates of change in heat, electricity, and fluid dynamics. In economics, derivatives describe marginal cost, revenue, and profit, allowing businesses to optimize production and pricing. They help in finding maximum or minimum points in data, crucial for decision-making. Thus, derivatives transform abstract calculus into practical tools across industries, giving precise insights into rates, optimization, and dynamic change.
Continuity ensures that functions behave predictably without sudden jumps, which is essential in physics, engineering, and economics. Calculus applies this principle to analyze growth, motion, optimization, and area under curves. For example, continuity ensures smooth motion in physics, while calculus models population growth, business profits, or the spread of disease. From designing roller coasters to forecasting financial markets, continuity and calculus enable accurate modeling of real-world systems, making them indispensable in applied sciences.
Begin with NCERT basics, ensuring clarity on limits, continuity, and differentiation. Move on to practice problems from standard references and past year JEE papers. Focus on conceptual understanding before memorizing formulas. Use error logs to track mistakes and revise frequently. Consistent practice of both solved examples and challenging problems ensures exam readiness. Time management and a structured study plan are essential.
Start with Functions and Graphs, then move to Limits and Continuity, followed by Differentiation. Once derivatives are strong, advance to Applications of Derivatives and finally Integration. This logical order mirrors the mathematical progression: definitions → limits → rates of change → applications → accumulation. Following this sequence ensures smooth learning and avoids conceptual gaps.
Review NCERT thoroughly, focusing on solved examples and exercises. Create concise notes with key formulas and theorems. Practice a variety of problems, from basics to higher-order, ensuring clarity in both concepts and applications. Use sample papers and previous exam questions to simulate test conditions. Finally, revise regularly with summary sheets and flashcards to reinforce memory before exams.