Rectangular Coordinate System in Space
Let ‘O’ be any point in space and →X'OX, →Y'OY and →Z'OZ be three lines perpendicular to each other. These lines are known as coordinate axes and O is called origin. The planes XY, YZ, ZX are known as the coordinate planes.
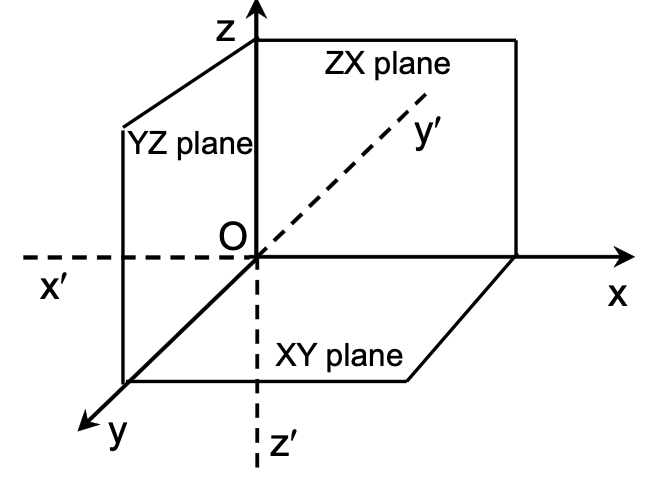
Coordinates of a Point in Space:
Consider a point P in space. The position of the point P is given by triad (x, y, z) where x, y, z are perpendicular distance from YZ-plane, ZX-plane and XY-plane respectively.
If we assume î, 𝕣, 𝕤 unit vectors along OX, OY, OZ respectively, then position vector of point P is xî + y𝕣 + z𝕤 or simply (x, y, z).

Note:
- x-axis = { (x, y, z) | y = z = 0 }
- y-axis = { (x, y, z) | x = z = 0 }
- z-axis = { (x, y, z) | x = y = 0 }
- xy plane = { (x, y, z) | z = 0 }
- yz plane = { (x, y, z) | x = 0 }
- zx plane = { (x, y, z) | y = 0 }
- OP = √x2 + y2 + z2
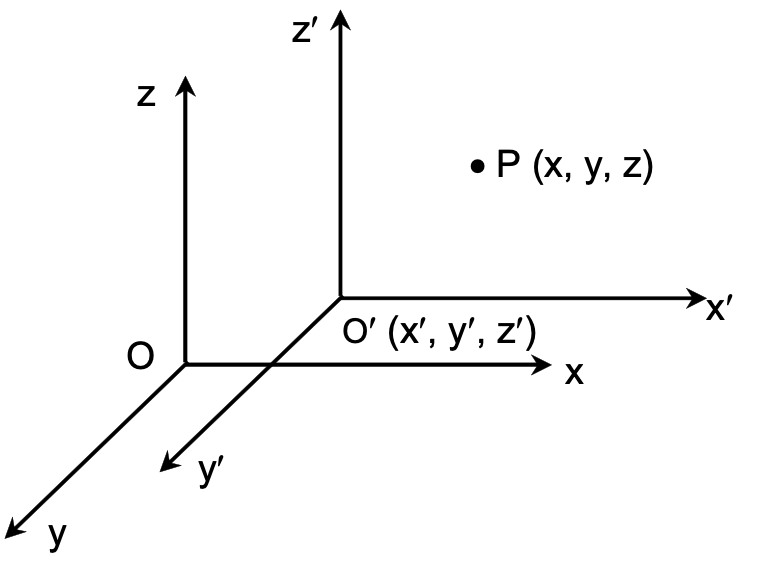
Shifting the Origin:
Shifting the origin to another point without changing the directions of the axes is called the translation of axes.
Let the origin O be shifted to another point
O' (x', y', z') without changing the direction of axes. Let the new coordinate frame be O'X'Y'Z'. Let P (x, y, z) be a point with respect to the coordinate frame OXYZ.
Then, coordinate of point P w.r.t. new coordinate frame O' X' Y' Z' is (x1, y1, z1), where
x1 = x – x', y1 = y – y', z1 = z – z'
Note:
- Distance between the points P(x1, y1, z1) and Q(x2, y2, z2) is
√[(x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2] - The point dividing the line joining P(x1, y1, z1) and Q(x2, y2, z2) in m : n ratio is
( (m x2 + n x1)/(m + n), (m y2 + n y1)/(m + n), (m z2 + n z1)/(m + n) ) where m + n ≠ 0 - The coordinates of centroid of a triangle having vertices A (x1, y1, z1), B (x2, y2, z2) and C (x3, y3, z3) is
G ( (x1 + x2 + x3)/3, (y1 + y2 + y3)/3, (z1 + z2 + z3)/3 )
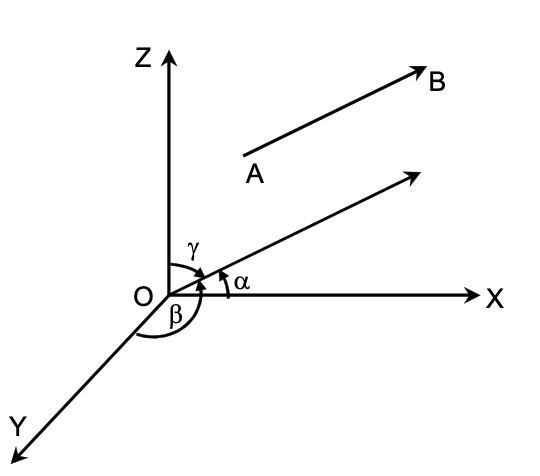
Direction Cosines of a Line
If α, β, γ be the angles which a given directed line makes with the positive directions of the co-ordinate axes, then cosα, cosβ, cosγ are called the direction cosines of the given line and are generally denoted by l, m, n respectively.
Thus, l = cosα, m = cosβ and n = cosγ
By the definition it follows that the direction cosine of the axis of x are respectively cos0°, cos90°, cos90° i.e. (1, 0, 0).
Similarly direction cosines of the axes of y and z are respectively (0, 1, 0) and (0, 0, 1).
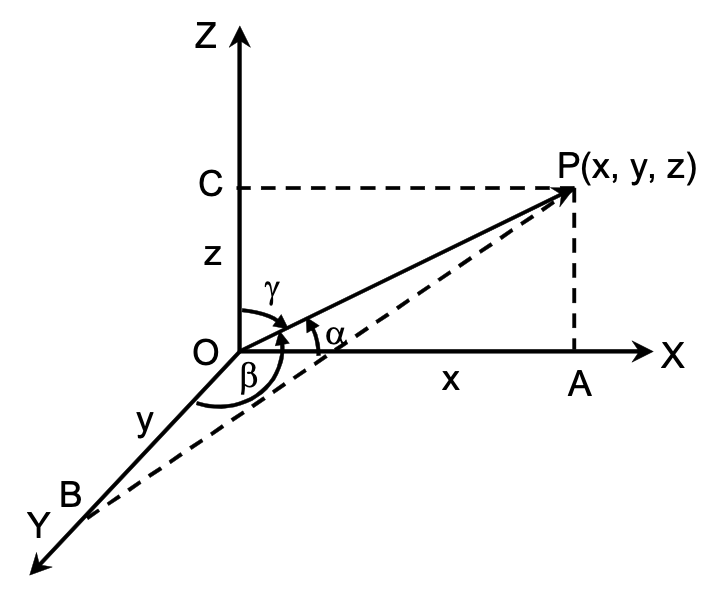
Relation between the Direction Cosines:
Let OP be any line through the origin O which has direction cosines l, m, n.
Let P ≡ (x, y, z) and OP = r
Then OP² = x² + y² + z² = r² …. (1)
From P draw PA, PB, PC perpendicular on the coordinate axes, so that
OA = x, OB = y, OC = z.
Also, ∠POA = α, ∠POB = β and ∠POC = γ.
From triangle AOP, l = cosα = x/r ⇒ x = lr
Similarly y = mr and z = nr
Hence from (1)
r²(l² + m² + n²) = x² + y² + z² = r² ⇒ l² + m² + n² = 1
Note:
- If the coordinates of any point P be (x, y, z) and l, m, n be the direction cosines of the line OP, O being the origin, then (lr, mr, nr) will give us the co-ordinates of a point on the line OP which is at a distance r from (0, 0, 0).
Direction Ratios:
If a, b, c are three numbers proportional to the direction cosine l, m, n of a straight line, then a, b, c are called its direction ratios. They are also called direction numbers or direction components.
Hence by definition, we have
l/a = m/b = n/c = k (say)
⇒ l = ak, m = bk, n = ck ⇒ k2(a2 + b2 + c2) = l2 + m2 + n2 = 1
⇒ k = ± 1 root a2 + b2 + c2 = ± 1∑a2
∴ l = ± a∑a2 . Similarly, m = ± b∑a2 and n = ± c∑a2
where the same sign either positive or negative is to be chosen throughout.
Example: If 2, –3, 6 be the direction ratios, then the actual direction cosines are 27 , –37 , 67 .
Parallel Lines:
Since parallel lines have the same direction, it follows that the direction cosines of two or more parallel straight lines are the same. So in case of lines, which do not pass through the origin, we can draw a parallel line passing through the origin and direction cosines of that line can be found.
Direction Cosine of a Line
Direction Cosine of a Line joining two given Points:
The direction ratios of line PQ joining P (x1, y1, z1) and Q(x2, y2, z2) are x2 - x1 = a (say), y2 - y1 = b (say), and z2 - z1 = c (say).
Then direction cosines are
l = (x2 - x1)⁄√Σ(x2 - x1)2, m = (y2 - y1)⁄√Σ(x2 - x1)2, n = (z2 - z1)⁄√Σ(x2 - x1)2
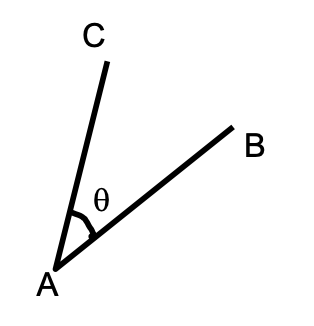
Angle between two Lines:
Let θ be the angle between two straight lines AB and AC whose direction cosines are given whose direction cosines are l1, m1, n1 and l2, m2, n2 respectively, is given by
cosθ = l1l2 + m1m2 + n1n2
If direction ratios of two lines are a1, b1, c1 and a2, b2, c2 are given, then angle between two lines is given by
cos θ = a1a2 + b1b2 + c1c2
√(a12 + b12 + c12) • √(a22 + b22 + c22)
Particular Results:
We have, sin2θ = 1 − cos2θ
= (l12 + m12 + n12)(l22 + m22 + n22) − (l1l2 + m1m2 + n1n2)2
= (l1m2 − l2m1)2 + (m1n2 − m2n1)2 + (n1l2 − n2l1)2
⇒ sinθ = ± √Σ(l1m2 − l2m1)2.
- Condition of perpendicularity:
If the given lines are perpendicular, then θ = 90° i.e. cos θ = 0
⇒ l1l2 + m1m2 + n1n2 = 0 or a1a2 + b1b2 + c1c2 = 0. - Condition of parallelism:
If the given lines are parallel, then θ = 0° i.e. sin θ = 0
⇒ (l1m2 – l2m1)2 + (m1n2 – m2n1)2 + (n1l2 – n2l1)2 = 0
which is true, only when
l1m2 – l2m1 = 0, m1n2 – m2n1 = 0 and n1l2 – n2l1 = 0 ⇒
l1/l2 = m1/m2 = n1/n2
Similarly, a1/a2 = b1/b2 = c1/c2.
Projection of a Line:
Projection of the line joining two point P (x1, y1, z1) and Q (x2, y2, z2) on another line whose direction cosines are l, m, n is
AB = l(x2 – x1) + m(y2 – y1) + n(z2 – z1)
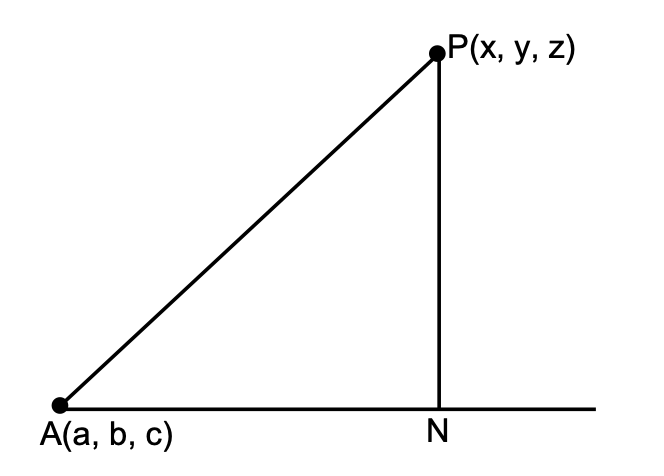
Perpendicular Distance of a Point from a Line
Perpendicular Distance of a Point from a Line:
Let AB is straight line passing through point A (a, b, c) and having direction cosines l, m, n.
AN = projection of line AP on straight line AB
―――――――――――――――――――――――
√(x − a)2 + (y − b)2 + (z − c)2
and AP = √(x − a)2 + (y − b)2 + (z − c)2
∴ perpendicular distance of point P
Area of a Triangle
Area of a Triangle
| y1 | z1 | 1 |
| y2 | z2 | 1 |
| y3 | z3 | 1 |
| x1 | z1 | 1 |
| x2 | z2 | 1 |
| x3 | z3 | 1 |
| x1 | y1 | 1 |
| x2 | y2 | 1 |
| x3 | y3 | 1 |
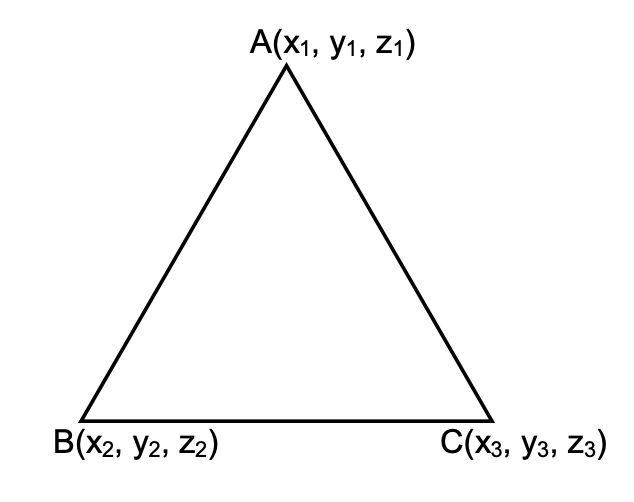
So, area of ΔABC is given by the relation Δ2 = Δx2 + Δy2 + Δz2
The Plane
Definition:
Consider the locus of a point P(x, y, z). If x, y, z are allowed to vary without any restriction for their different combinations, we have a set of points like P. The surface on which these points lie, is called the locus of P. It may be a plane or any curved surface. If Q be any other point on its locus and all points of the straight line PQ lie on it, it is a plane. In other words if the straight line PQ, however small and in whatever direction it may be, lies completely on the locus, it is a plane, otherwise any curved surface.
Equation of Plane in Different Forms:
- General equation of a plane is ax + by + cz + d = 0
- Equation of the plane in Normal form is lx + my + nz = p where p is the length of the normal from the origin to the plane and (l, m, n) be the direction cosines of the normal.
- The equation to the plane passing through P(x₁, y₁, z₁) and having direction ratios (a, b, c) for its normal is a(x − x₁) + b(y − y₁) + c(z − z₁) = 0
- The equation of the plane passing through three non-collinear points (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) is
| (x − x₁) (y − y₁) (z − z₁) | | (x₂ − x₁) (y₂ − y₁) (z₂ − z₁) | = 0 | (x₃ − x₁) (y₃ − y₁) (z₃ − z₁) |
- The equation of the plane whose intercepts are a, b, c on the x, y, z axes respectively is x/a + y/b + z/c = 1 (a b c ≠ 0)
- Equation of YZ plane is x = 0, equation of plane parallel to YZ plane is x = d.
Equation of ZX plane is y = 0, equation of plane parallel to ZX plane is y = d.
Equation of XY plane is z = 0, equation of plane parallel to XY plane is z = d.
- Four points namely A (x1, y1, z1), B (x2, y2, z2), C (x3, y3, z3) and D (x4, y4, z4) will be coplanar if one point lies on the plane passing through other three points.
Angle between the Planes
Angle between the planes is defined as angle between normals of the planes drawn from any point to the planes.
Angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is
√[(a12 + b12 + c12)(a22 + b22 + c22)] )
- If a1a2 + b1b2 + c1c2 = 0, then the planes are perpendicular to each other.
- If a1/a2 = b1/b2 = c1/c2 then the planes are parallel to each other.
Perpendicular Distance:
The length of the perpendicular from the point P(x1, y1, z1) to the plane ax + by + cz + d = 0 is
Family of Planes:
Equation of plane passing through the line of intersection of two planes u = 0 and v = 0 is u + λv = 0.
Intersection of a Line and Plane:
If equation of a plane is ax + by + cz + d = 0, then direction cosines of normal to this plane are a, b, c. So angle between normal to the plane and a straight line having direction cosines l, m, n is given by
Then angle between the plane and the straight line is π/2 − θ.
- Plane and straight line will be parallel if al + bm + cn = 0
- Plane and straight line will be perpendicular if a/l = b/m = c/n
Bisector Planes of Angle between two Planes:
The equation of the planes bisecting the angles between two given planes \( a_1x + b_1y + c_1z + d_1 = 0 \) and \( a_2x + b_2y + c_2z + d_2 = 0 \) is
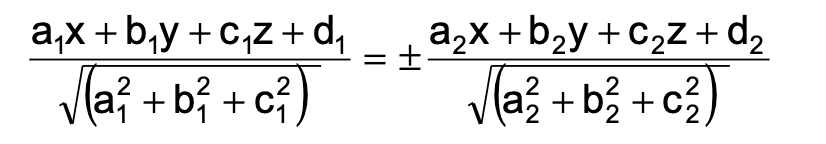
THE STRAIGHT LINE
Straight line in three dimensional geometry is defined as intersection of two planes. So general equation of straight line is stated as the equations of both plane together i.e. general equation of straight line is a1x + b1y + c1z + d1 = 0, a2x + b2y + c2z + d2 = 0 ……(1)
So, equation (1) represents straight line which is obtained by intersection of two planes.
Equation of Straight Line in Different Forms:
Symmetrical Form:
- Equation of straight line passing through point P (x1, y1, z1) and whose direction cosines are l, m, n is
x−x1 l = y−y1 m = z−z1 n - Equation of straight line passing through two points P (x1, y1, z1) and Q (x2, y2, z2) is
x−x1 x2−x1 = y−y1 y2−y1 = z−z1 z2−z1
Note:
The general coordinates of a point on a line is given by (x1 + l r, y1 + m r, z1 + n r) where r is distance between point (x1, y1, z1) and point whose coordinates is to be written.
Shortest Distance between two non Intersecting Line:
Two lines are called non intersecting lines if they do not lie in the same plane. The straight line which is perpendicular to each of non-intersecting lines is called the line of shortest distance. And length of shortest distance line intercepted between two lines is called length of shortest distance.
Method:
Let the equation of two non-intersecting lines be
x - x1/l1 = y - y1/m1 = z - z1/ n1 = r1 (say).... (1)
And x - x2/l2 = y - y2/m2 = z - z2/ n2 = r2 (say).... (2)
Any point on line (1) is P (x1 + l1r1, y1 + m1r1, z1 + n1r1) and on line (2) is
Q (x2 + l2r2, y2 + m2r2, z2 + n2r2).
Let PQ be the line of shortest distance. Its direction ratios will be
[(l1r1 + x1– x2– l2r2), (m1r1 + y1– y2– m2r2), (n1r1 + z1– z2– n2r2)]
This line is perpendicular to both given line. By using condition of perpendicularity we obtain 2 equations in r1 and r2.
So by solving these, values of r1 and r2 can be found. And subsequently point P and Q can be found. The distance PQ is shortest distance.
The shortest distance can be found by PQ

Note: If any straight line is given in general form then it can be transformed into symmetrical form and we can further proceed.
The Sphere
A sphere is a locus of a point which moves in space such that its distance from a fixed point is constant. Fixed point is called centre of sphere and constant distance is called radius of sphere.
Equation of Sphere in Different Forms:
- If centre of sphere is (a, b, c) and radius is r, then equation of sphere is
(x – a)² + (y – b)² + (z – c)² = r². - If centre of sphere is origin and radius is r, then x² + y² + z² = r².
- General form: The general equation of a sphere is
x² + y² + z² + 2ux + 2vy + 2wz + d = 0
Centre of sphere = (–u, –v, –w), radius = √(u² + v² + w² – d). - Diameter form: Equation of a sphere whose extremities of diameter are A (x1, y1, z1) and B (x2, y2, z2) is
(x – x1)(x – x2) + (y – y1)(y – y2) + (z – z1)(z – z2) = 0.
Frequently Asked Questions
Three-dimensional geometry, often called 3D geometry, is the study of objects in space that have length, width, and height. Unlike two-dimensional shapes (such as squares or circles), three-dimensional figures include cubes, spheres, cones, and cylinders. This branch of mathematics is important because it mirrors the real world—most physical objects around us are three-dimensional.
In school mathematics, 3D geometry introduces concepts such as coordinates in space, vectors, planes, and distances between points. It helps students develop spatial reasoning, which is essential not only for exams like CBSE or JEE but also for real-life applications in engineering, architecture, robotics, and computer graphics.
Students often start by learning the basic terms—coordinate axes (x, y, z), direction cosines, and vector operations—before applying them to solve problems on distance, section formula, equations of lines, and planes. Building confidence in these topics requires practice and a stepwise approach, beginning with NCERT examples before attempting higher-level problems.
For learners, the key is to link theory with visual imagination. Using diagrams, 3D models, or software tools can significantly improve understanding. By mastering this subject, students not only prepare well for exams but also gain a foundation for STEM careers.
Preparation for 3D geometry requires a systematic approach because the subject blends theoretical concepts with problem-solving. For Class 12 or competitive exams, the following steps can serve as a roadmap:
|
Step |
Focus Area |
Strategy |
|
1 |
NCERT Basics |
Start with Class 12 NCERT chapters to understand coordinate geometry in 3D and vector algebra. |
|
2 |
Concept Clarity |
Focus on direction cosines, equations of lines and planes, shortest distance, and angles. |
|
3 |
Problem Practice |
Solve a wide variety of problems, starting with worked examples and moving to previous year papers. |
|
4 |
Visual Learning |
Draw diagrams for every problem to strengthen visualization. |
|
5 |
Revision & Short Notes |
Create formula sheets for distance, dot product, cross product, and angles between planes. |
The realization of three dimensions emerged naturally from human experience. Everything in our environment can be described using length, width, and height. Ancient civilizations recognized this while constructing buildings, designing tools, and mapping stars. For example, builders needed to measure not just flat areas but also volumes to design structures like pyramids and temples.
Mathematically, the idea became formalized with the development of coordinate systems. René Descartes introduced the Cartesian system in the 17th century, allowing us to represent points using (x, y, z). This gave geometry a structured framework and allowed scientists to extend earlier two-dimensional methods to three dimensions.
Philosophically, space was always seen as multidimensional. Philosophers like Aristotle and Kant wrote about the structure of space and time. Modern science later extended the idea, with Einstein showing that time could be considered a fourth dimension.
Thus, our recognition of three dimensions is both practical (through observation of the physical world) and theoretical (through mathematics and philosophy). Studying this history provides deeper appreciation of how geometry is not just a subject but a reflection of how humans understand reality.
Three-dimensional geometry (3D geometry) is the branch of mathematics that deals with objects having length, breadth, and height. Unlike two-dimensional geometry (2D), which only considers flat figures like triangles, circles, and rectangles, 3D geometry includes shapes such as spheres, cones, cubes, cuboids, and cylinders.
The key difference lies in the third dimension depth which adds volume to shapes. For example:
- A square (2D) becomes a cube (3D).
- A circle (2D) becomes a sphere (3D).
In mathematics education, 3D geometry typically covers coordinate geometry in space. This involves points, lines, planes, distances, angles, and equations of different objects in three dimensions.
A practical example is in architecture and engineering: designing a building requires knowledge of 3D geometry to calculate space, volume, and alignment. Similarly, computer graphics, robotics, and navigation rely heavily on 3D coordinate systems.
In exams (like CBSE Class 11/12 or JEE), students solve problems based on finding distances, midpoints, direction cosines, or equations of planes and lines in 3D space.
3D geometry connects mathematical theory with real-world spatial understanding, making it crucial for both academic success and practical applications.
The field of 2D geometry has been studied for centuries and includes countless theorems and results because most early human observation (land, surfaces, drawings) was naturally two-dimensional. In contrast, 3D geometry is relatively newer and often overlaps with vector algebra, calculus, and physics.
In education, 3D is usually restricted to manageable topics like lines, planes, and distances to keep the curriculum practical and aligned with student learning capacity. Expanding it further would require introducing more advanced mathematics, which is usually done at higher levels (engineering, physics, computer science).
Thus, 3D geometry is not less important—it is simply taught in a focused, exam-relevant way at the school level.
For CBSE and similar boards, 3D geometry is divided between Class 11 and 12:
|
Class 11 Topics |
Class 12 Topics |
|
Distance between two points in 3D space |
Direction cosines and direction ratios |
|
Section formula in 3D |
Equation of a line in 3D |
|
Midpoint formula in 3D |
Equation of a plane |
|
Introduction to 3D coordinate geometry |
Angle between two lines or a line and a plane |
|
Distance of a point from a plane |
- Follow NCERT textbook as primary resource.
- Practice all solved examples before attempting exercises.
- Use previous board exam papers to identify recurring question patterns.
- Focus on short-answer numerical questions, which often come directly from solved examples.
- Create a formula sheet covering equations of lines and planes.
Yes, NCERT is sufficient for board-level preparation since almost all CBSE exam questions are derived from it. However, students aiming for competitive exams (JEE/NEET) should practice additional reference books and problem banks for application-based learning.
In JEE Main, 3D geometry typically carries around 6–8 marks, which may equal 1–2 questions. In JEE Advanced, it is often integrated with vector algebra or calculus questions, making it an essential high-yield topic.
While the weightage may seem small, 3D geometry is considered scoring because the problems are formula-based and can be solved quickly if practiced well.
- Start with NCERT basics (distance formula, section formula).
- Move to direction cosines, equations of lines and planes.
- Practice previous year JEE questions specifically on 3D.
- Use short notes and formula sheets for revision.
- Attempt mock tests to gain speed and accuracy.
By following this order, even a beginner can cover 3D geometry in 2–3 weeks with consistent effort.