Distance Between Two Points
Let A and B be two given points, whose coordinates are given by A(x1, y1) and B(x2, y2) respectively. Then
AB = √[(x1 − x2)2 + (y1 − y2)2]
Section Formula
Coordinates of point P dividing the join of two points A(x1, y1) and B(x2, y2) internally in the given ratio λ1 : λ2 are
P ( ((λ2x1 + λ1x2) / (λ2 + λ1), (λ2y1 + λ1y2) / (λ2 + λ1) ) )
Coordinates of point P dividing the join of two points A(x1, y1) and B(x2, y2) externally in the ratio λ1 : λ2 are
P ( ((λ2x1 − λ1x2) / (λ2 − λ1), (λ2y1 − λ1y2) / (λ2 − λ1) ) )
Centroid
The point of concurrency of the medians of a triangle is called the centroid of the triangle. The centroid of a triangle divides each median in the ratio 2 : 1. The coordinates are given by
G ≡ ( (x1 + x2 + x3) / 3, y1 + y2 + y3) / 3 ) )
Orthocentre
The point of concurrency of the altitudes of a triangle is called the orthocentre of the triangle. The coordinates of the orthocentre of the triangle A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) are ( (x₁ tan A + x₂ tan B + x₃ tan C) / (tan A + tan B + tan C), (y₁ tan A + y₂ tan B + y₃ tan C) / (tan A + tan B + tan C) ) .
Incentre
The point of concurrency of the internal bisectors of the angles of a triangle is called the incentre of the triangle. The coordinates of the in centre are given by I ≡ ( (a x₁ + b x₂ + c x₃) / (a + b + c), (a y₁ + b y₂ + c y₃) / (a + b + c) ) where a, b and c are lengths of the sides BC, CA and AB respectively.
Circumcentre
The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcentre of the triangle. The coordinates of the circumcentre of the triangle with vertices A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) are ( (x₁ sin 2A + x₂ sin 2B + x₃ sin 2C) / (sin 2A + sin 2B + sin 2C), (y₁ sin 2A + y₂ sin 2B + y₃ sin 2C) / (sin 2A + sin 2B + sin 2C) ) .
Centroid divides the line joining orthocentre and circumcentre in 2 : 1 internally.
Area of a Triangle
Let (x1, y1), (x2, y2), and (x3, y3) respectively be the coordinates of the vertices A, B, C of a triangle ABC. Then the area of triangle ABC is:
(1/2) | x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) | = Modulus of (1/2)
| x1 | y1 | 1 |
| x2 | y2 | 1 |
| x3 | y3 | 1 |
Exa.: The area of the triangle with vertices at (p–4, p+5), (p+3, p–2) and (p, p) is
(A) 3p + p2
(B) |p| + 5
(C) |p – 3|
(D) none of these
Solution: (D). The area of triangle is
| p–4 | p+5 | 1 |
| p+3 | p–2 | 1 |
| p | p | 1 |
= (1/2)
| –4 | 5 | 0 |
| 3 | –2 | 0 |
| p | p | 1 |
(R1 → R1 – R3, R2 → R2 – R3)
= |(1/2)(8–15)| = 7/2 sq. units,
which remains constant for all values of p.
Procedure for Finding the Equation of the Locus of a Point
- If we are finding the equation of the locus of a point P, assign coordinates (h, k) to P.
- Express the given conditions as equations in terms of the known quantities to facilitate calculations. We sometimes include some unknown quantities known as parameters.
- Eliminate the parameters, so that the eliminant contains only h, k and known quantities.
- Replace h by x, and k by y, in the eliminant. The resulting equation would be the equation of the locus of P.
- If x and y coordinates of the moving point are obtained in terms of a third variable t (called the parameter), eliminate t to obtain the relation in x and y and simplify this relation. This will give the required equation of locus.
Straight Line
Any equation of first degree of the form Ax + By + C = 0, where A, B, C are constants always represents a straight line (at least one out of A and B is non-zero).
Slope
If θ is the angle at which a straight line is inclined to the positive direction of x axis, slope of the line is m = tanθ, 0 ≤ θ < 180° (θ ≠ 90°).
Standard Equations of Straight Lines
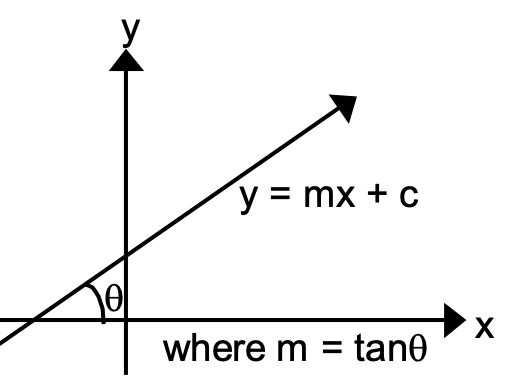
Slope Intercept Form
y = mx + c,
where m = slope of the line = tanq
c = y intercept
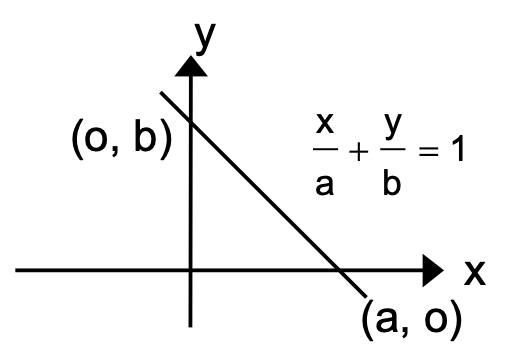
Intercept Form
x/a + y/b = 1
x intercept = a
y intercept = b
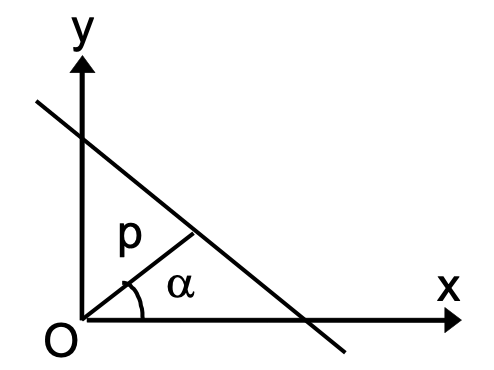
Normal Form
x cosa + y sina = p, where a is the angle which the perpendicular to the line makes with the axis of x and p is the length of the perpendicular from the origin to the line. p is always positive.
Slope Point Form
Equation: y - y1 = m(x - x1), where
(a) One point (x1, y1) on the straight line (x1, y1)
(b) The direction of the straight line i.e., the slope of the line = m
Two Point Form:
Equation: y − y1 = y2 − y1⁄x2 − x1 (x − x1) ,
where (x1, y1) and (x2, y2) are the two given points. Here m = y2 − y1⁄x2 − x1 .
Parametric Form
To find the equation of a straight line which passes through a given point A(h, k) and makes a given angle θ, with the positive direction of the x-axis.
P(x, y) is any point on the line LAL′.
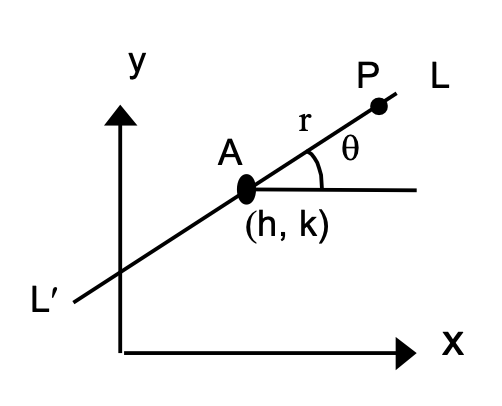
Let AP = r. x − h = r cosθ y − k = r sinθ
x − hcosθ=y − ksinθ=r is the equation of the straight line LAL′.
Any point on the line will be of the form (h + r cosθ, k + r sinθ) and for any value of r this will represent a point on the straight line. Here | r | gives the distance of the point P from the fixed point (h, k).
Position of Two Points with respect to a Given Line
Let the given line be ax + by + c = 0 and P(x1, y1), Q(x2, y2) be two points. If the quantities ax1 + by1 + c and ax2 + by2 + c have the same signs, then both the points P and Q lie on the same side of the line ax + by + c = 0.
If the quantities ax1 + by1 + c and ax2 + by2 + c have opposite signs, then they lie on the opposite sides of the line.
Angle between Two Straight Lines
If θ is the acute angle between two lines, then
where m1 and m2 are the slopes of the two lines and are finite.

Notes:
- If the two lines are perpendicular to each other then m1m2 = -1.
- Any line perpendicular to ax + by + c = 0 is of the form bx – ay + k = 0.
- If the two lines are parallel or are coincident, then m1 = m2.
- Any line parallel to ax + by + c = 0 is of the form ax + by + k = 0.
The Distance between Two Parallel Lines
The distance between two parallel lines:
ax + by + c₁ = 0 and ax + by + c₂ = 0 is
|c₁ − c₂|
√(a² + b²)
Length of the Perpendicular from a Point on a Line
The length of the perpendicular from P(x₁, y₁) on ax + by + c = 0 is
|ax₁ + by₁ + c|
√(a² + b²)
The Distance between Two Parallel Lines
The distance between two parallel lines:
ax + by + c₁ = 0 and ax + by + c₂ = 0 is
|c₁ − c₂|
√(a² + b²)
Length of the Perpendicular from a Point on a Line
The length of the perpendicular from P(x₁, y₁) on ax + by + c = 0 is
|ax₁ + by₁ + c|
√(a² + b²)
Equation of the Bisector of the Angles between Two Lines
Equation of the Bisector of the Angles between Two Lines
Consider two lines L1 and L2 represented as:
L1 ≡ a1x + b1y + c1 = 0
and L2 ≡ a2x + b2y + c2 = 0.
Let P (x, y) be any point on either of bisectors.
Perpendicular distance of P from L1 = Perpendicular distance of P from L2
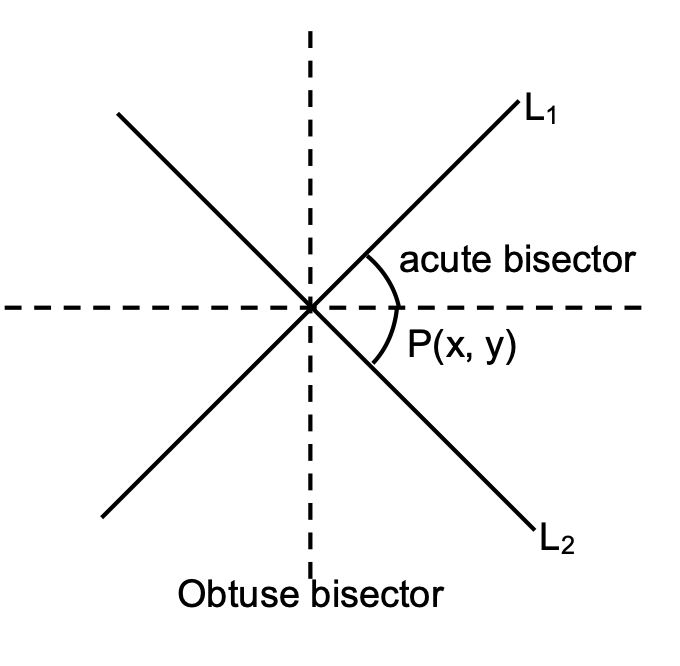
Taking c1 > 0, c2 > 0 and (a1b2 ≠ a2b1)
| Conditions | Acute angle bisector | Obtuse angle bisector |
|---|---|---|
| A1a2 + b1b2 > 0 | − | + |
| A1a2 + b1b2 < 0 | + | − |
FAMILY OF LINES
The general equation of the family of lines through the point of intersection of two given lines is
L + lL¢ = 0, where L = 0 and L¢ = 0 are the two given lines, and l is a parameter. Conversely any line of the form L1 + l L2 = 0 passes through a fixed point which is the point of intersection of the lines L1 = 0 and L2 = 0.
Concurrency of Straight Lines
The condition for three lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0, a₃x + b₃y + c₃ = 0 to be concurrent is
-
a₁ b₁ c₁
a₂ b₂ c₂
a₃ b₃ c₃ = 0 - There exist three constants l, m, n (not all zero at the same time) such that
lL₁ + mL₂ + nL₃ = 0, where L₁ = 0, L₂ = 0, and L₃ = 0 are the three given straight lines. - The three lines are concurrent if any one of the lines passes through the point of intersection of the other two lines.
Pair of Straight Lines
The general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of straight lines if abc + 2fgh − af2 − bg2 − ch2 = 0 and h2 ≥ ab.
The homogeneous second degree equation ax2 + 2hxy + by2 = 0 represents a pair of straight lines through the origin if h2 ≥ ab.
m₁ + m₂ = −2h/b, m₁m₂ = a/b
If θ be the angle between two lines, through the origin, then
tan θ = ± √(m1 + m2)2 − 4m1m2
1 + m1m2 = ± 2√h2 − ab
a + b .
The lines are perpendicular if a + b = 0 and coincident if h2 = ab.
Joint Equation of Pair of Lines joining the Origin and Points of Intersection of a Curve and a Line:
If the line lx + my + n = 0, ((n ≠ 0) i.e., the line does not pass through origin) cut the curve ax² + 2hxy + by² + 2gx + 2fy + c = 0 at two points A and B, then the joint equation of straight lines passing through A and B and the origin is given by homogenizing the equation of the curve by the equation of the line. i.e.,
ax² + 2hxy + by² + (2gx + 2fy) ( (lx + my)/-n ) + c ( (lx + my)/-n )2 = 0
is the equation of the lines OA and OB.
Formula and Concepts
- The equation of the straight line passing through the point P(x1, y1) and Q(x2, y2) is
y - y1 = (y2 - y1)/(x2 - x1)(x - x1) or| x y 1 | | x₁ y₁ 1 | = 0 | x₂ y₂ 1 |
- The equation of the straight line, for which the length of the perpendicular from the origin is p and the perpendicular makes an angle α with the positive x-axis, is
x cosα + y sinα = p. - The equation of the line passing through the point P(x1, y1) and making an angle θ with the positive x-axis is
(x - x1)/cosθ = (y - y1)/sinθ = r (parametric form)
where r is the distance of any point (x1 ± r cosθ, y1 ± r sinθ) on the line from P(x1, y1). - Let θ be the acute angle between two straight lines y = m1x + c1 and y = m2x + c2. Then
tanθ = | (m1 - m2) / (1 + m1m2) | - The lines are parallel if tanθ = 0 ⇒ m1 = m2.
- The lines are perpendicular if θ = 90° ⇒ m1m2 = -1.
- The equation of any line passing through the intersection of these lines is < b>a1x + b1y + c1 + λ(a2x + b2y + c2) = 0 where λ is an arbitrary constant.
- The three lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0, a3x + b3y + c3 = 0 are concurrent if
| a₁ b₁ c₁ | | a₂ b₂ c₂ | = 0 | a₃ b₃ c₃ |
- The perpendicular distance of the point P(x1, y1) from the line ax + by + c = 0 is
|a x1 + b y1 + c|
——————————————
√(a2 + b2) - The equations of the bisectors of the angle between the lines ax1 + by1 + c1 = 0, ax2 + by2 + c2 = 0 are
(a1x + b1y + c1) / √(a12 + b12) = ± (a2x + b2y + c2) / √(a22 + b22)
- The second degree equation ax2 + by2 + 2hxy + 2gx + 2fy + c = 0 represents a pair of lines if
h2 ≥ ab and abc + 2gfh − af2 − bg2 − ch2 = 0. - The angle θ between these lines is given by tanθ = ± √(h2 − ab) / (a + b) so that the lines are parallel or coincident if h2 = ab and perpendicular to each other if a + b = 0.
Frequently Asked Questions
Mastering straight lines and coordinate geometry requires a systematic approach. Start by understanding the basic principles of geometry, such as the concept of a line, its equation, and how to represent lines graphically on a coordinate plane. Progressively tackle more complex topics like slope, intercepts, and equations of lines. Utilize practice problems from multiple sources and apply these concepts to solve real-world problems. A deep dive into key formulas like the point-slope form and general form of the equation will help you gain mastery. Use visual aids and graph plotting tools to reinforce understanding. Consistent practice is essential, especially for preparing for exams like IIT JEE, where problem-solving under time pressure is key.
The best approach to prepare for straight lines in IIT JEE is to understand the core concepts thoroughly, focusing on slope, point-slope form, and various types of line equations. Work on different forms like slope-intercept, general, and normal forms. Solve a variety of problems from previous JEE exams, focusing on problem-solving speed. Conceptual clarity in geometry and algebra is crucial. Ensure you’re comfortable with applications such as finding the equation of a line passing through two points, the angle between two lines, and distance from a point to a line. Use JEE-specific study materials, attend coaching sessions if needed, and regularly review solved examples for practice.
The intersection of circles and straight lines is a vital area in JEE preparation. First, revise the basic equations of circles and lines. Then, focus on their interaction: finding points of intersection, tangents to circles, and properties of tangents from external points. Understand the derivation of the equation of the tangent to a circle and work on applying these concepts to solve complex problems. Regular practice of previous years' papers and mock tests is essential. You should also make sure to review the relationship between the radius, slope of the tangent, and the geometry of lines intersecting circles.
A straight line is a one-dimensional geometric object that has no curvature and extends infinitely in both directions. It is defined by two points, and the shortest distance between any two points on the line is the straight line itself. Mathematically, a straight line in a 2D plane is represented by the equation y = mx + c, where m is the slope and c is the y-intercept. This line can be visualized as the path traced by an object moving in a constant direction.
A straight line represents the simplest and most fundamental geometric concept. It’s important because it serves as the foundation for much of geometry and algebra, especially in coordinate systems. Straight lines are crucial for modeling linear relationships in real life, such as speed-distance-time problems, economics, and physics. The study of straight lines enables the understanding of slope, intercepts, and relationships between variables, which are central to fields such as calculus, algebra, and computer graphics.
Mathematicians define lines to provide a consistent framework for understanding spatial relationships and geometric structures. A line, whether straight or curved, is defined based on its properties, such as direction, length, and position in space. The formalization of lines allows mathematicians to apply various mathematical principles across different fields, including algebra, trigonometry, and calculus. For straight lines, definitions focus on properties like slope, intercepts, and the equation of the line.
The equation of a pair of straight lines is given by the general form of the equation of the second-degree curve, Ax2 + By2 + 2Gxy + 2Fx + 2Gy + C = 0, where AAA, BBB, CCC, GGG, and FFF are constants. This equation represents two straight lines when the discriminant of the quadratic form is zero. The process to find the pair of lines involves determining the values of these constants from the given conditions.
To find the equations of two lines from a pair of straight lines, we need to manipulate the general form of the second-degree equation. First, split the given equation into its linear factors by factoring it. The factorization will give us the individual line equations, which can be written in slope-intercept form or general form. This method is crucial in solving problems related to pairs of straight lines in coordinate geometry.
Through any two distinct points, exactly one straight line can be drawn. This is a basic concept in geometry, where the uniqueness of a straight line passing through two points is guaranteed. The equation of this line can be determined using the point-slope form or slope-intercept form once the coordinates of the two points are known.
In the physical world, there are no perfectly straight lines due to imperfections at the atomic and molecular levels. Even the straightest man-made objects or natural formations have some form of curvature when examined at a microscopic scale. However, for most practical purposes, we can consider straight lines as idealized concepts that serve as useful approximations in physics and engineering.
Nature rarely exhibits perfectly straight lines due to the inherent irregularities in the material world. Forces like gravity, wind, and the growth patterns of plants or geological formations cause natural structures to deviate from perfect straightness. However, in human-made structures and scientific modeling, straight lines are used to simplify complex natural phenomena, providing clearer understanding and predictions.
While straight lines do not exist in a perfectly physical sense, they are fundamental mathematical abstractions used to represent idealized relationships and concepts. In geometry, a straight line is defined as having no curvature and extending infinitely in both directions. While real-world lines are never perfectly straight, the concept of a straight line is a useful model for understanding and solving various real-world problems.