Statics and dynamics

Mechanics is a science which deals with the behavior of a body or bodies under the influence of forces and their mutual interaction. Statics is that branch of mechanics which deals with the action of forces, in equilibrium, acting on bodies at rest. 

Whatever we see, feel or perceive around by any of our five senses and which occupies space is called matter. Scrap of matter with no size at all, but with a definite position is called a particle. In other words, particle is position of matter which is infinitesimally small in size. A body is a portion of matter occupying a bounded space, and is composed of infinite number of particles. A body is said to be a rigid body if the distance between any two particles of the body always remain constant i.e. a rigid body does not change its shape and size when subjected to external forces. 

To each particle, there corresponds a unique real number, called its mass and the mass of a particle does not change at all. The mass of a body is the sum of the masses of its constituent particles. In other words, mass of a body is the quantity of matter it contains. In metric system, a gram is taken to be the unit of mass and is equivalent to the mass of cubic centimeter of distilled water at 4°C. Density is mass per unit volume. 

If the volume and mass of a body are V and m respectively, then m = Vρ, where ρ is the density of the substance of the body. A particle is said to be at rest, if it does not change its position relative to its surroundings and a body is at rest if each particle of the body is at rest. A body is said to be in motion, if its position changes relative to its surroundings. 

FORCE

A force is an external agency or cause which changes or tends to change the state of rest or of motion of a particle / body. The amount of force acting on a particular body is called the magnitude of force. The point in the body where the force acts is called the point of application of the force. The line of action of the force gives the direction of the force. A force is completely known if its: (i) magnitude, (ii) direction, and (iii) point of application at known. The force is, thus, a vector quality, and is a localized vector. The standard international (SI) unit of force is newton, denoted by N, (A newton is that force which when acts on rigid body of mass one kilogram produces an acceleration of 1 m/sec2).

• Action and Reaction:

When two bodies, say A and B, are in contact with each other, each will exist a certain force on the other at their point of contact. The force exerted by the first body (A) on the second body (B) is called the force of action and the force exerted by B and A is called reaction. According to Newton’s third law of motion, these two forces are equal in magnitude but opposite in direction and act along the common normal at their point of contact. 

• Tension and Thrust: 

If a force acts by means of a string or a spring, it is called tension (or pull) and if a force acts by means of a rod, it is called thrust ( or push). 

• Attraction and Repulsion: The force exerted between two unconnected bodies without any visible means is called the force of attraction, if the bodies tend to approache each other. The force, on the other hand, is called force of repulsion if the two bodies tend to move away from each other. 

Do Check: Differential equation

Force System

When a number of forces act simultaneously on a particle or a rigid body, these forces form a force system.

For example, consider a body placed on a smooth inclined plane, acted by a force along the plane surface. The forces acting on the body are: 

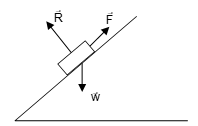
(i) its weight

(ii) reaction of the plane on the body

(iii) the applied force

• A force system or a system of forces is said to be coplanar, if the lines of action of all the forces lies in the same plane. If the lines of action of all the forces do not lie in same plane, the system is non-coplanar force system. 
• A system of forces is said be collinear if all the forces have a common line of action. 
• If the lines of action of all the forces meet in a point, the system is concurrent force system. 
• A force system is said to be a parallel force system if the lines of action of all the forces are parallel to each other. 
• When two or more forces act upon a particle (or rigid body), and the particle (or the body) remain at rest, the forces are said to be inequilibrium. A force system in equilibrium may be added to or removed from another force system without affecting the change in position of rest (or motion) produced by the later system. 

COMPOSITION AND RESOLUTION OF FORCES

• Resultant Force:

If two or more forces P, Q, S,… act upon a rigid body and if a single force, R, can be found whose effect upon the body is the same as that of the forces P, Q, S, … this single force R is called the resultant of the given forces and the given forces P, Q, S,… are called the components of R.

Resultant of forces acting in the same direction (same straight line) is equal to their sum.

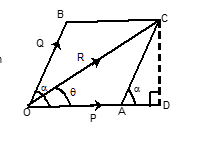
LAW OF PARALLELOGRAM OF FORCES

If two forces, acting at a point, are represented in magnitude and direction by the two sides of a parallelogram drawn from one of its angular points, their resultant is represented both in magnitude and direction by the diagonal of the parallelogram passing through that angular point.

Let OA and OB represent the forces P and Q, in magnitude and direction, acting at a point O and inclined to each other at an angle α = ∠AOB. Also OA = P, OB = Q.

Then the resultant R and its direction θ (shown in figure) will be given by:

tan θ = (Q sin α) / (P + Q cos α)

and

R = √(P² + Q² + 2 P Q cos α)

• Resolution of a force:

A force may be resolved into two components in an infinite number of ways, because an infinite number of parallelograms can be constructed on the line of action of a given force. The most important case of the resolution of forces occurs when we resolve a force into two components at right angles to one another. The resolved part of a given force in a given direction is the component in the given direction which, with a component in a direction perpendicular to the given direction, is equivalent to the given force.

• Components of a Force in Two given Directions: 

Let F be the given force represented in magnitude and direction by OC and let the directions of the two components be along OL and OM.

Also ∠COL = α and ∠COM = β. 

Let the components of F along OL and OM be F1 and F2 respectively. Taking OA = F1 and OB = F2 = AC, complete the parallelogram OACB. Then ∠OCA = β, 

and ∠OCA = π− (α + β).

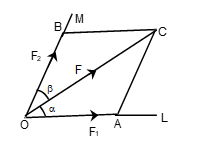
Applying sine rule to the triangle OAC, we get

F₁ = F sin β
sin(α + β) and F₂ = F sin α
sin(α + β)

• Now in the above situation if α+β = 90°, then F₁ = F cos α and F₂ = F sin α.
• When a given force is resolved into two directions which are at right angles to each other, then its component in these directions are called resolved parts of the given force. Clearly, the resolved part of a given force in a given...

Do Check: Matrix

Triangle of Forces:

If three forces, acting at a point, are represented in magnitude and direction by the sides of a triangle, taken in order, they will be in equilibrium.

Remark: 

• In the triangle of forces it must be carefully noted that the forces must be parallel to the sides of a triangle taken in order, i.e. taken the same way round.

Converse of the Triangle of forces:

If three forces acting at a point are in equilibrium they may be represented in magnitude and direction by the sides of any triangle which is drawn so as to have its sides respectively parallel to the directions of the forces.

Lami's Theorem

If three forces acting on a particle keep it in equilibrium, each is proportional to the sine of the angle between the other two.

Illustration 1: The resultant of two forces P and Q is R. If Q is doubled, R is doubled and when Q is reversed, R is again doubled, then P : Q : R is equal to

1. √2 : √3 : √2
2. √3 : √2 : √3
3. √2 : √3 : √1
4. none of these

(A). Let α be the angle between the forces P and Q.

Now from the given conditions, we have

R² = P² + Q² + 2PQ cosα ...(1)

and

(2R)² = P² + (2Q)² + 2P(2Q) cosα

⇒ 4R² = P² + 4Q² + 4PQ cosα ...(2)

and

(2R)² = P² + (−Q)² + 2P(−Q) cosα

⇒ 4R² = P² + Q² − 2PQ cosα ...(3)

Adding (1) and (3), we get 2P² + 2Q² − 5R² = 0

Eliminating α from (2) and (3), we get

P² + 2Q² − 4R² = 0

From (4) and (5), we have

^P2⁄₋₈ + ^Q2⁄₋₁₀ + ^R2⁄₋₈ = ^P2⁄₂ + ^Q2⁄₃ = ^R2⁄₂

So, P : Q : R = √2 : √3 : √2

Do Check: Determinant

Illustration 2: Forces M and N acting at a point O make an angle 150°. Their resultant acts at O, has magnitude 2 units and is perpendicular to M. Then, in the same unit, the magnitudes of M and N are

1. 2√3 , 4
2. √3, 2√2
3. 4, 3
4. 4, 5

(A). We have 2² = M² + N² + 2MN cos150° ...(1)

π/2 = M sin150° / (M + N cos150°) ... (since resultant is perpendicular to M)

and tan π/2 = M sin150° / (M + N cos150°) ⇒ M + N cos150° = 0

Solving (1) and (2), we get M = 2√3 and N = 4.

Illustration 3: If a body is in equilibrium under the action of three co-planar forces then

(A) they must act in a straight line

(B) they must meet in a point or must be parallel

(C) their horizontal and vertical components are equal 

(D) none of these 

Solution: (A) Force must meet in a point or they must be parallel.

Illustration 4: A beam whose centre of gravity divides it into two portions a and b, is placed inside a smooth horizontal sphere. If θ be its inclination to the horizon in the position of equilibrium and 2α be the angle subtended by beam at the centre of the sphere then

the angle subtended by beam at the centre of the sphere then

(A) tanθ = (b - a)/(b + a) tan α

(B) tanθ = (b - a)/(b + a) tan α

(C) tanθ = (b + a)/(b - a) tan α

(D) tanθ = 1/(b - a)(b + a)

Solution: (B). Applying m–n theorem in ΔABO, we get

(AG+GB) cot∠OGB = GB cot∠OAB - AG cot∠OBG

⇒ (a+b) cot(90°–θ) = b cot( π/2 – α ) – a cot( π/2 – α )

⇒ (a + b) tanθ = b tanα – a tanα

⇒ tanθ = (b - a)/(b + a) tan α

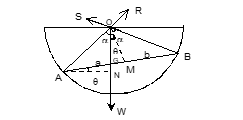
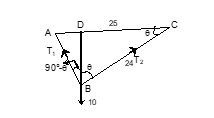
Illustration 5 : A body of mass 10kg is suspended by two strings 7 cm and 24 cm long, their other ends being fastened to the extremities of a rod of length 25 cm. If the rod be so held that the body hangs immediately below its middle point, then the tensions of the strings are

(A) 14/5, 48/5

(B) 4/5, 8/5

(C) 9/5, 18/5

(D) none of these

Solution: (A). Clearly, ΔABC is right angled at B. Also BD is

median and we know that

BD =DC ⇒∠DCB = ∠DBC = θ (say)

Here, sinθ = 7/25 or cosθ = 24/25

Applying Lami’s Theorem 10/sin 90° = T₂/sin(90° + θ) = T₁/sin(180° – θ)

⇒ T₁ = 10 sinθ = 14/5 and T₂ = 48/5

Exercise 1

(i) The maximum resultant of two forces is P and the minimum resultant is Q, the two forces are at right angles, the resultant is

(ii) The resultant R of two forces P and Q act at right angles to P. Then the angle between the forces is

(iii) A uniform rod AB, 17 m long whose mass is 125 kg rests with one end against a smooth vertical wall and the other end on a smooth horizontal floor, this end being tied by a chord 8 metres long, to a peg at a bottom of the wall, the tension of the chord is

Polygon of Forces

If any number of forces, acting on a particle, be represented, in magnitude and direction, by the sides of a polygon, taken in order, the forces will be in equilibrium.

Important deductions

• The resultant of two forces, acting at a point O in directions OA and OB and represented in magnitude by λ. OA and μ. OB is represented by (λ+μ). OC, where C is a point in AB such that λ.CA = μ.CB.

• The sum of the resolved parts of two forces in a given direction is equal to the resolved part of their resultant in the same direction.

• If the forces acting on a particle are in equilibrium, the algebraic sum of their resolved parts in two directions at right angles are separately zero.

• Conversely, if the sum of their resolved parts in two directions at right angles separately vanish, the forces are in equilibrium.

Parallel Forces

Forces whose lines of action are parallel are called parallel forces. Parallel forces are of two types:

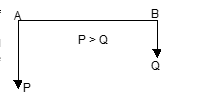
(i) Like parallel forces

If two forces acting at different points of a rigid body be such that their lines of action are in the same direction, we say that the forces are like parallel forces.

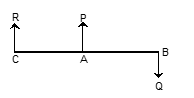
In the figure, two forces P and Q act at two different points A and B of a rigid body such that their lines of action are in the same direction and hence, they are called like parallel forces, where P > Q.

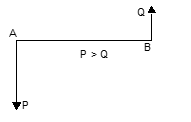
(ii) Unlike parallel forces:

If two forces acting at different points of a rigid body be such that their lines of action are in opposite directions, we say that the forces are unlike parallel forces.

In the figure, two forces P and Q act at two different points A and B of a rigid body such that the line of action of the force P is opposite to the line of action of the force Q and therefore the two given forces P and Q are called unlike parallel forces, where P > Q.

Notes:

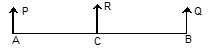
• The resultant of two like parallel forces P and Q acting at A and B is equivalent to a force P + Q acting in the same direction at C, a point in AB such that AC = Q × BC.

• If P > Q, then CA < BC, i.e. the resultant R = P + Q will act at a point nearer to the larger force and farther from the smaller one.

  P/BC=Q/AC=P+Q/AC+BC=R/AB i.e. each force P, Q, and R respectively is proportional to the distance between the other two.

• The resultant of two unlike parallel forces of magnitude P and Q (P > Q), acting at points A and B of a rigid body is a force of magnitude P − Q, parallel to them in the direction of the greater force P and acts at point C, which divides AB externally in the ratio Q : P, i.e. P/BC=Q/AC=R/AB

• In case of equal unlike force (P = Q), it is not possible to find a single force having the same effect as the combined effect of the two forces. Such a pair of forces constitutes a couple.

MOMENTS

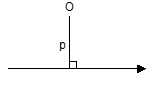
When a force is applied to a rigid body in such a way that every particle of the body moves through the same distance, the body is said to undergone have motion of translation. If, on the other hand, a force is applied to a body such that each particle of the body describes a circle with a fixed point of the body as centre, the body is said to undergo the motion of rotation. The moment of a force about that point is the measure of its turning effect about the point and is equal to the product of the force and perpendicular distance of its line of action from the point.

Vector Moment of a Force:

If F be a force acting at the point A and O be a fixed point in space, so that the position vector of A with respect to O is r.

The moment of F about O is given by:

M = r × F

The magnitude of M is:

|M| = |r| × |F| × sinθ = pF

where p is the perpendicular distance from O on the line of action of F.

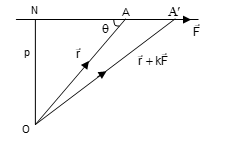
If we take a point A′ on the line of action of force F, the position vector of A′ is r + kF. The moment of F acting at A′ is:

(r + kF) × F = r × F

The moment is, thus, unaltered by sliding the force along its line of action.

Hence, the sum of the vector moments about a point O of forces P, Q, R, … acting at a point A is equal to the vector moment about O of their single resultant force:

P + Q + R + …

Positive and Negative Moments

• The moment of a force about a point measures the tendency of the force to cause rotation about that point. If the tendency of the force is to turn the lamina in anti-clockwise direction, the usual convention is to regard the moment as positive, and that in clockwise direction as negative.
• The algebraic sum of the moments of a set of forces about a given point is the sum of the moments of the forces, each moment having its proper sign prefixed to it.
• The algebraic sum of the moments of any two forces about any point in their plane is equal to the moment of their resultant about the same point.
• If any number of forces in one plane acting on a rigid body have a resultant, the algebraic sum of their moments about any point in their plane is equal to the moment of their resultant.
• The moment of a force about an axis is the product of the resolved part of the force in a direction perpendicular to the axis (the other component being the product of force parallel to the axis) and the shortest distance between the axis and the line of the force.

Couples

A system of two equal and unlike parallel forces, whose lines of action are not the same, is called a couple or a torque.

• Moment of Couple: The moment of a couple is the product of one of the forces forming the couple and the arm of the couple. The perpendicular distance between the lines of action of the forces is called the arm of the couple.
• The moment of the couple is regarded as positive or negative according as it has a tendency to turn the body in the anti-clockwise or clockwise direction.
• The algebraic sum of the moments of the two forces forming a couple about any point in their plane is constant, and is equal to the moment of the couple.
• Two couples acting in one plane upon a rigid body, whose moments are equal and opposite, balance one another.
• Any number of couples in the same plane acting on a rigid body are equivalent to a single couple, whose moment is equal to the algebraic sum of the moments of the couples.
• If three forces, acting upon a rigid body, are represented in magnitude, direction, and line of action by the sides of a triangle taken in order, they are equivalent to a couple whose moment is represented by twice the area of the triangle.

Illustration 6: P and Q are two like parallel forces acting at A and B respectively. If P is moved parallel to itself through a distance d on AB, then the resultant of P and Q moves through a distance:

1. Pd / (P + Q)
2. Pd / (P - Q)
3. pd / (P+Q)
4. none of these

Solution

Let the resultant of two parallel forces P and Q act at point C; then:

P/BC = Q/AC = R/AB

⇒

P/BC = Q/AC = (P + Q)/AB ...(1)

Now let P be moved parallel to itself from the point A to A′. The resultant in this case is also moved to a point C′. Then:

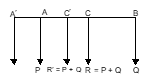
P/BC′ = Q/AC′ = R/A′B

From (1): BC = (P × AB) / (P + Q) ...(3)

From (2): BC′ = (P × AB) / (P + Q) ...(4)

Now:

CC′ = BC′ − BC = (P / (P + Q)) × (A′B − AB) = (P × AA′) / (P + Q)

= (P × d) / (P + Q), where AA′ = d (given).

Illustration 7: A heavy rod AB, 20 cm long rests horizontally on two pegs 10 cm apart. Loads of 10 kg and 1 kg are hung from A and B respectively. If the reactions at the pegs are equal, then the distance of the pegs from the middle point of the rod is:

1. 2/21 cm
2. 18/21 cm
3. 20/18 cm
4. 20/21 cm

Solution: (D)

Let the rod AB be placed on the pegs C and D.
AB = 20 cm; AC = BD = 5 cm.
Then CD = 10 cm.

Let W denote the weight of the rod acting at G, and suppose GC = x so that GD = 1 × x.

• Now suppose 10 kg weight is suspended from A. In this case, the rod will tilt about C so that there will be no reaction at D.
  Taking moment about C:

  W × x = 10 × 10 = 100 ...(1)

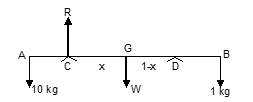
• Similarly, when 1 kg weight is suspended from B, we shall have:

  W × (1 − x) = 1 × 5 = 5 ...(2)

From (1) and (2), x = 20/21 cm.

Exercise 2: If the position of the resultant of two like parallel forces P and Q is unaltered, when the positions of P and Q are interchanged, then:

1. P = Q
2. P = 2Q
3. 2P = Q
4. none of these

3. Forces forming a couple are of magnitude 12N each and the arm of the couple is 8 m. The force of an equivalent couple whose arm is 6 m is of magnitude:
   1. 8N
   2. 16N
   3. 12N
   4. 4N
4. A rod can turn freely about one of its ends, which is fixed. At the other end a horizontal force equal to half the weight of the body is acting. In the position of equilibrium, the rod is inclined to the vertical at an angle:
   1. 30°
   2. 45°
   3. 60°
   4. None of these

Dynamics

Dynamics is the science of motion and the particle dynamics is one of the simplest branches of applied Mathematics. In the Mathematical model we employ rectangular axes (as a rigid frame of reference) and assign to each position of the particle set of three numbers say (x, y, z), the coordinates of the point. The set of all points which a particle occupies during its motion is called the path or the trajectory of the particle.

If the path is a straight line, the motion is said to be rectilinear. Otherwise, it is said to be curvilinear. The measure of the succession of points occupied by the particle during its motion is called time.

Speed of a moving point or particle is the rate at which the point or the particle is describing its path. In other words, speed is the distance covered by a particle in one unit of time. If s is the total distance moved in time t, then average speed is s / t.

At each instant, a particle occupies a certain position on its path. Let P and Q be the positions of the particle at instants t and t + Δt respectively. If O is a fixed point on the path and s and s + Δs are the distances of P and Q from O respectively, the distance traversed by the particle in time Δt is Δs. The average speed in this short interval of time is Δs / Δt. In the limit of Δt → 0, ds/dt is called the instantaneous speed (or simply speed) of the particle at the instant t.

The change of position of a particle, in a given interval of time, is called displacement of the particle in that interval. Displacement of a particle from P to Q is a vector quantity and is denoted by PQ.

The rate of displacement of a particle is called its velocity. Velocity is, thus, a vector quantity and its magnitude is same as the speed of the particle.

Let O be a fixed point on OA, the initial line. Let P and Q be the positions of a particle at time t and t + Δt respectively, so that PQ is the displacement of the particle during the time interval Δt.

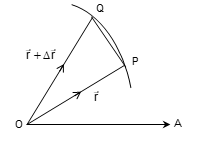
Let r = OP, r + Δr = OQ. Then PQ = Δr. Thus velocity v of the particle, at time t, is:

v = ds/dt

= speed of the particle at time t.

The acceleration a at P is given by:

a = lim(Δt→0) Δv / Δt = dv/dt

Acceleration and Retardation

a = d/dt (dr/dt) = d²r/dt²

For the rectilinear motion, r = xi, and v = dx/dt i, a = d²x/dt² i = dv/dt i = (dv/dx)(dx/dt) i = v (dv/dx) i

Negative acceleration (decrease in the magnitude of velocity) is known as retardation.

If a particle has two or more velocities simultaneously, it cannot move in two or more directions at the same time. It moves in a fixed direction with a fixed velocity. This fixed velocity is called the resultant velocity of the given two or more velocities. These two or more velocities are called the component velocities of the resultant velocity.

Parallelogram Law of Velocities

If a particle possesses two simultaneous velocities which are represented in magnitude and direction by two sides of a parallelogram drawn from a point, these velocities are equivalent to a velocity which is represented in magnitude and direction by the diagonal of the parallelogram passing through that point.

Let u and v be the velocity vectors of a particle at O and let α be the angle between them. Then, if V is the resultant velocity:

|V| = √(|u|² + |v|² + 2|u||v|cosα) ...(1)

If θ is the angle which the resultant velocity makes with the direction of velocity u, then:

tanθ = (|v|sinα) / (|u| + |v|cosα) ...(2)

• If u and v are perpendicular to each other, then α = π/2, |V| = √(|u|² + |v|²), and tanθ = |v| / |u|.
• If u and v are in the same direction, then α = 0 ⇒ |V| = |u| + |v| and tanθ = 0 ⇒ θ = 0.
• If u and v are in the opposite directions, then |V| = (|u| − |v|) and θ = 0.
• If |u| > |v|, then |V| = |u| − |v| and has the same direction as u.
• If |u| < |v|, then |V| = |v| − |u| and has the direction opposite to that of u.
• If u and v are of equal magnitude i.e., u = v, then |V| = 2|u|cos(α/2) and tanθ = (sinα) / (1 + cosα) = tan(α/2).

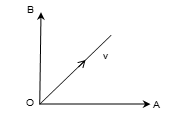
Let OA and OB be two perpendicular lines. If the velocity V of magnitude |V| at O is inclined at an angle φ with OA, then components u and v of V along OA and OB are:

u = |V|cosφ, v = |V|sinφ

Law of Motion

Relative to a basic frame of reference, the motion of a particle of mass m, subjected to a force F, is governed by the equation:

F = kma

where a is the acceleration of the particle at time t and k is a constant.

If F = 0, a = 0 ⇒ dv/dt = 0 ⇒ v is constant. Thus, under the influence of no force, a particle moves with constant velocity, i.e., it travels in a straight line with constant speed.

We choose the units of mass, time, and forces in such a way that k = 1. These units are called dynamical units and then the equation of motion becomes:

F = ma = m d²r/dt² = m dv/dt

Law of Action and Reaction

Two particles exert forces on each other which are equal and opposite and act along the line joining the two particles.

Rectilinear Motion

When a particle or a body moves in a straight line, the motion is said to be rectilinear motion.

Equations of Motion

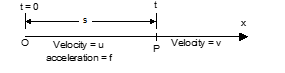
A particle moves along a straight line with initial velocity u and constant acceleration f from a fixed point. If v be the velocity acquired in time t and s be the distance travelled by the particle in time t. Then:

1. v = u + ft
2. s = ut + 1/2 ft²
3. v² = u² + 2fs

Remark:

• If the particle moves in a straight line with a retardation f, then we put −f in place of f.
• v = u − ft
• s = ut − 1/2 ft²
• v² = u² − 2fs

Above formulae are valid only if the acceleration is uniform throughout the motion.

Distance Travelled in a Particular Time

If a particle starts with initial velocity u m/sec and uniform acceleration f m/sec², the distance travelled in the nth second is given by:

Sₙ = u + (1/2)f[2n − (u(n − 1) + (1/2)f(n − 1)²] = u + (1/2)f(2n − 1)

Average Velocity

Suppose a particle moves in a straight line with initial velocity u m/sec and constant or uniform acceleration f m/sec². If v is the velocity of the particle at time t, then its average velocity during the interval of time t is given by:

(u + v) / 2 = u + (1/2) f t

Distance travelled in time t is:

s = ut + (1/2) f t²

Motion in a Straight Line Under Gravity

It was observed by Galileo that all bodies which are allowed to fall from a height at a given place in vacuum have the same constant acceleration. This acceleration is due to the gravitational attraction of the body by the Earth towards its centre. It is denoted by 'g' and is numerically equal to the force with which the earth attracts a unit mass towards its centre.

The value of g does not remain constant; it changes from place to place. It increases with the altitude of the place and has the greatest value at the poles and the least at the equator. But the variation in the values is nearly half percent. Therefore for all numerical calculations the value of g is taken as constant. In SI system the value of g is 9.8 m/sec².

Equations for Vertical Motion

Case I:

A particle is projected vertically downwards from a point O with velocity u and at time t, it is at a point P such that OP = h and v is its velocity at P. Then the equations describing its motion are:

v = u + gt ...(1) h = ut + (1/2) g t² ...(2) v² = u² + 2gh ...(3) hₙ = u + (1/2) g(2n − 1) ...(4)

Case II:

If the particle is falling down freely (u = 0), then:

v = gt ...(1) h = (1/2) g t² ...(2) v² = 2gh ...(3) hₙ = (1/2) g(2n − 1) ...(4)

Case III:

If the particle is projected vertically upward with a velocity u and at any time t, it is at a point P such that OP = h and velocity at P is v, then:

v = u − gt ...(1) h = ut − (1/2) g t² ...(2) v² = u² − 2gh ...(3) hₙ = u − (1/2) g(2n − 1) ...(4)

Greatest height attained (v = 0 in (3)):

h = u² / (2g) ...(5)

Additional Equations

Time to the greatest height (v = 0 in (1)):

t = u / g ...(6)

Time to a given height h:

t = (u ± √(u² − 2gh)) / g (from (2))

Notes:

• Time from any point on the path to the highest point is same as the time from the highest point to the given point when the body is returning.
• The particle at the same point passes with same magnitude of velocity whether going upward or coming downward.

Illustration 8: A car is moving at 30 m/s and a man rolls a ball across the floor of the car at right angles to the direction of motion of the car at 10 m/s. Then the resultant velocity of the ball is:

1. 10√10 m/s
2. 10 m/s
3. 2√10 m/s
4. None of these

Solution:

Let u = 30 m/s and v = 10 m/s.
Since the two velocities are at right angles, the resultant:

|V| = √(u² + v²) = √(30² + 10²) = √(900 + 100) = 10√10 m/s

If the resultant makes an angle φ with the direction of the car, then:

tanφ = 10 / 30 = 1 / 3 ⇒ φ = tan⁻¹(1 / 3)

Illustration 9: A body whose velocity is being constantly accelerated has at certain instant a velocity of 22 m/sec and in the following minute, it travels a distance of 10320 m. Find the acceleration:

1. 4 m/sec²
2. 5 m/sec²
3. 6 m/sec²
4. 3 m/sec²

Solution: s = ut + (1/2) f t² => f = 2(10320 − 1320) / 3600 = 5 m/sec²

Illustration 10: The velocity of a train increases from 15 km/hr to 60 km/hr while it moves through a distance of 1/8 km. If the acceleration is uniform, find its magnitude:

1. 26/25 m/sec²
2. 27/25 m/sec²
3. 24/25 m/sec²
4. 28/25 m/sec²

Solution:

u = 15 km/hr = 25/6 m/sec, v = 60 km/hr = 50/3 m/sec
s = 1/8 km = 125 m

v² = u² + 2fs => (50/3)² = (25/6)² + 2 × f × 125 => f = 24/25 m/sec²

Illustration 11: The height from which a body will fall if it dropped 75 m during the last second of the fall (g = 10 m/sec²) is:

1. 320 m
2. 110 m
3. 220 m
4. 300 m

Solution:

Let the body fall for t seconds. Distance covered in nth second = 1/2 g(2t − 1)

(1/2) × 10 × (2t − 1) = 75 => t = 8 sec

Thus, body falls for 8 seconds.

Let h be the height from which the body falls:

h = (1/2) g t² = (1/2) × 10 × (8)² = 320 meters

Hence, the body falls from a height of 320 meters.

Exercise 3

(i) The displacements of a particle moving along a straight line is related to time by the relation t = √s + 3, where s is in meters and t is in seconds. The displacement in meters of particle when its velocity is zero is given by:

1. 0
2. -2m
3. 2m
4. 1m

(ii) A body is moving in a straight line with uniform acceleration. It covers distances of 10 m and 12 m in the third and fourth second respectively. The initial velocity of the body will be:

1. 2 m/sec
2. 3 m/sec
3. 4 m/sec
4. 5 m/sec

(iii) A bullet moving at 100 m/sec is fired into a wood-block in which it penetrates 50 cm. If the same bullet moving with the same velocity were fired into a similar piece of wood but only 12.5 cm thick, then the velocity with it emerges is:

1. 500 m/sec
2. 500/√3 m/sec
3. 500√3 m/sec
4. None of these

RELATIVE VELOCITY

Definition:

When two points P and Q move in the same plane, the rate of change of position of P with respect to Q (i.e., as seen from Q) is defined as the relative velocity of P with respect to Q and it is denoted by v_PQ.

Let the two points P and Q move in the same plane with velocities v_P and v_Q, represented by the vectors PT and QR respectively.

From parallelogram PQRS, PS represents v_PQ in magnitude and direction. By the triangle law of velocities, we have:

ST = PT − PS i.e., v_PQ = v_P − v_Q or v_P + (−v_Q)

Hence the relative velocity of P with respect to Q is obtained by compounding with the actual velocity of P a velocity equal and opposite to that of Q.

Determination of Relative Velocity

If two points P and Q are moving with velocities u and v respectively along two straight lines intersecting at an angle α, then:

|v_PQ| = √(u² + v² − 2uv cos α) ...(1) tan θ = (v sin α) / (u − v cos α) ...(2)

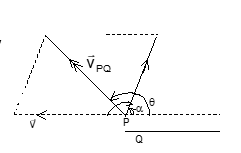
The relations (1) and (2) give the magnitude and direction of v_PQ.

Notes:

• • If the points P and Q be moving in the same direction with velocity u and v (u ≤ v) then v_PQ = u − v (in the direction of P).
  • If the points P and Q be moving in the opposite directions, then v_PQ = u + v (in the direction of P).
  • In case the two points P, Q are moving with velocities u, v at angles α, β with x-axis, and v_R be the velocity of P and relative to Q inclined at an angle β to the x-axis then:

v cos θ = u cos α − v cos β v sin θ = u sin α − v sin β

Illustration 12: To a man walking due east at the rate of 4 km/hr, the wind appears to blow from the North-East at 4√2 km/hr. Then the true velocity of the wind is:

1. 4 km/hr
2. 2 km/hr
3. 6 km/hr
4. None of these

Solution:

(A) u = 4, v = 4√2, α = 135°

u = velocity of observer
v = apparent velocity of wind
w = true velocity of wind

w = √(u² + v² + 2uv cos α) = √(4² + (4√2)² + 2(4)(4√2)(-1/√2)) = 4 km/hr

tan θ = (4√2 sin 135°) / (4 + 4√2 cos 135°) i.e., θ = π/2

Hence the wind is actually blowing from north at 4 km/hr.

Shortest Distance Between Two Points in Motion

The actual way in which the distance between two points, which are both moving, or the direction of one as seen from other at different instants, may be estimated by considering the actual motions of both points during the interval, or equally well, by assuming one to be at rest and making the other move with relative motion.

Thus the shortest distance between them can be obtained by taking the perpendicular distance of one of the points from the relative path of the second with respect to the first.

Exercise 4

(i) A train is travelling along a horizontal rail at the rate of 60 km/hr and rain is driven by the wind which is in the same direction as the motion of the train, so that it falls with a velocity 30 km/hr at an angle of 30° with the vertical. The apparent direction of the rain to a person travelling with the train is at:

1. 45° with the vertical
2. tan⁻¹(1/2) with the vertical
3. 60° with its true direction
4. Right angles to its true direction

(ii) To a man running at a speed of 20 km/hr, the rain drops appear to be falling at an angle of 30° with the vertical. If the raindrops are actually falling vertically downwards, their velocity is:

1. 10 km/hr
2. 10√3 km/hr
3. 20√3 km/hr
4. 40 km/hr

(iii) A man is running with a velocity of 6 miles per hour in a shower of rain which is falling vertically with a velocity of 12 miles per hour. If θ be the angle which the apparent direction of the rain makes with the vertical then tan θ =

1. 2
2. 1/3
3. 2/3
4. None of these

Projectile

If a body is thrown from a point into the air space inclined at an angle to the horizontal, it describes a curved path. The path described by the body, i.e., the projectile, is called its trajectory.

To completely consider the motion of a projectile, the size of the body, the resistance of air, and variation in the force of gravity with height are taken into account. With all these parameters, the problem of motion of a projectile is rather complex. We, therefore, simplify and idealize it by:

• Regard the body as a particle, ignoring the resistance offered by the air atmosphere.
• Taking the gravitational force as constant throughout the motion.
• The particle is called a projectile.
• The point from which the particle is projected is called the point of projection.
• The angle that its direction makes with the horizontal plane through the point of projection is called the angle of projection.
• The path which the particle describes is called its trajectory.
• The distance between the point of projection and the point where the path meets any horizontal plane drawn through the point of projection is called range on the plane.
• The time that elapses before it again meets the horizontal plane through the point of projection is called the time of flight.
• The initial velocity with which the projectile is projected is called the velocity of projection.
• The maximum height reached by a projectile during its motion is called greatest height.

Motion of a Projectile Under Gravity

Let the mass of the particle be m. Let the initial position of the particle at time t = 0 be taken as O. Take OX along the horizontal and OY along the vertical at O.

Let the particle be projected at O with velocity u making an angle α with the horizontal OX. Let P(x, y) be the position of the particle at time t. The only force acting on the particle during its flight is the force of gravitation mg acting along OY.

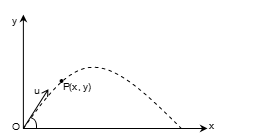
The components of the initial velocity along OX and OY respectively are u cos α, and u sin α. The equations of motion in the x-plane, along the horizontal and the vertical are:

The trajectory of the projectile is parabolic with vertex at:

(u² sin α cos α / g , u² sin² α / 2g)

It follows that the greatest height attained during the motion is:

H = u² sin² α / 2g

The maximum horizontal distance (range) traversed is:

R = u² sin 2α / g

• Velocity and direction of motion after time t are given by: v² = u² − 2ugt sin α + g²t²
  tan θ = (u sin α − gt) / (u cos α)
• Velocity and direction of motion at height h: v² = u² − 2gh
  tan θ = √(u² sin² α − 2gh) / (u cos α)
• Greatest height attained by a projectile: h = u² sin² α / 2g
• Time for the greatest height: t = (u sin α) / g
• Time of flight: T = 2u sin α / g

Answer to Exercises

Exercise 1

• (i) D
• (ii) B
• (iii) D
• (iv) A

Exercise 2

• (i) A
• (ii) B
• (iii) B

Exercise 3

• (i) A
• (ii) D
• (iii) C
• (iv) C
• (v) A

Exercise 4

• (i) D
• (ii) C
• (iii) B
• (iv) D

Formulae and Concepts at a Glance

1. Let OA and OB represent the forces P and Q, in magnitude and direction, acting at a point O and inclined to each other at an angle α = ∠AOB. Also OA = P, OB = Q.
2. Then the resultant R and its direction θ (shown in figure) will be given by:

   R = √(P² + Q² + 2PQ cos α) and

   tan θ = (Q sin α) / (P + Q cos α)

3. Lami’s Theorem: If three forces acting on a particle keep it in equilibrium, each is proportional to the sine of the angle between the other two.
4. The resultant of two forces, acting at a point O in directions OA and OB and represented in magnitude by λ. OA and μ. OB is represented by (λ+μ). OC, where C is a point in AB such that λ.CA = μ.CB.
5. The sum of the resolved parts of two forces in a given direction is equal to the resolved part of their resultant in the same direction.
6. If the forces acting on a particle are in equilibrium, the algebraic sum of their resolved parts in two directions at right angles are separately zero.
7. Conversely, if the sum of their resolved parts in two directions at right angles separately vanish, the forces are in equilibrium.

Solved Examples

1. Three forces P, Q, R are acting at a point in a plane. The angle between P and Q, Q and R are 150° and 120° respectively, then for equilibrium, forces P, Q, R are in the ratio:

1. 1 : 2 : 3
2. 1 : 2 : √3
3. 2 : 1 : 3
4. √3 : 2 : 1

Solution:

(D) Forces are as marked in the figure. By Lami's Theorem, we have:

P / sin 120° = Q / sin 90° = R / sin 150°

P / (√3/2) = Q / 1 = R / (1/2)

P / √3 = Q / 2 = R / 1

∴ P : Q : R = √3 : 2 : 1

2. Two unlike parallel forces P and Q act at points 5 m apart. If the resultant force is 9N and acts at a distance of 10/3 m from the greater force P, then:

1. P = 16N, Q = 7N
2. P = 15N, Q = 7N
3. P = 27N, Q = 18N
4. P = 18N, Q = 9N

Solution:

The resultant of P and Q acts at C. Therefore:

AC = (AB × Q) / (P − Q) = (10 × Q) / (P − Q) = 10 × (5/9)

Q = 18N, P = Q + 9 = 27N

3. Three like parallel forces P, Q, R act at the corner points of a triangle ABC. Their resultant passes through the circumcentre. Then:

1. P = Q = R
2. P = Q = 2R
3. P + Q + R = 0
4. None of these

Solution:

(C) Since the resultant passes through the circumcentre of ΔABC, the algebraic sum of the moments about it is zero. Hence:

P + Q + R = 0

4. If r and r' be the maximum ranges up and down the inclined plane respectively and R be the maximum range on horizontal plane, then r, R, r' are in:

1. A.P
2. G.P
3. H.P
4. None of these

Solution:

(C) Consider:

1/r + 1/r' = (4 / u²g) [1 + (sin β + 1 − sin β)] = 2 / u²g

∴ r, R, r' are in H.P.

5. An aeroplane A is flying at a level height towards North with a speed of 800 km/hr as observed from the ground. Its pilot observes that another plane B at the same level height is flying at 600 km/hr towards west. The velocity of the aeroplane B as observed from the ground is:

1. 1000 km/hr, tan⁻¹(3/4) west of north
2. 500 km/hr, tan⁻¹(3/4) west of north
3. 1000 km/hr, tan⁻¹(3/4) west of north
4. None of these

Solution:

(C) v_AB = √(v_NA² + v_WA² + 2(v_NA)(v_WA) cos α)

= √(800² + 600²) (α = π/2) = 1000 km/hr

tan θ = v_WA / v_NA = 3/4
θ = tan⁻¹(3/4) with the north.

6. A bullet fired into a target loses half its velocity after penetrating 3 cm. How much further will it penetrate?

1. 1 cm
2. 2 cm
3. 3 cm
4. 4 cm

Solution:

(A) v² = u² − 2fs ⇒ (u/2)² = u² − 2f × 3 ⇒ f = u² / 8

After penetrating 3 cm, initial velocity will become u/2.

So, v² = u² − 2fs ⇒ 0 = (u/2)² − 2 × (u² / 8) × s ⇒ s = 1 cm.

7. A train which is moving at the rate of 36 km/hr is brought to rest in 2 minutes with a uniform retardation. Find the retardation and also the distance that the train travels before coming to rest:

1. 500 meters
2. 600 meters
3. 400 meters
4. 700 meters

Solution:

(B) u = 36 km/hr = 10 m/sec, v = 0, u − at = 0 ⇒ a = u/t = 10 / 120 = 1/12 m/sec²

Now, v² = u² − 2fs ⇒ 0² = (10)² − 2 × (1/12) × s ⇒ s = 600 meters.

8. Find the distance described during the tenth second by a particle having initial velocity of 60 m/sec and moving with a retardation of 2 m/sec². Find the time in which it comes to rest:

1. 31 m, 20 sec
2. 41 m, 30 sec
3. 21 m, 20 sec
4. 51 m, 20 sec

Sol. (B). s_n = u - 1/2 f(2n - 1) = 60 - 1/2 × 2 × (2 × 10 - 1) = 60 - 19 = 41 meters

And v = u - ft = 60 - 2 × t ⇒ t = 30 seconds

9. Two equal forces at a point. If the square of the magnitude of their resultant is three times the product of their magnitudes, the angle between the forces is

• (A) 30°
• (B) 45°
• (C) 90°
• (D) 60°

Sol. (D). Let the angle between two equal forces each of magnitude P be α. Then, the resultant is 2P cos(α/2).

By hypothesis, we have √3P² = 2P cos(α/2) ⇒ cos(α/2) = 1/2 ⇒ α = 60°.

10. If R and R′ are the resultant of two forces P and Q (P > Q) according as they are like or unlike such that R : R′ = 25 : 7, then P : Q =

• (A) 2 : 1
• (B) 3 : 4
• (C) 4 : 3
• (D) 1 : 2

Sol. We have, P/Q + Q/P = R/P and P/Q - Q/P = R′/P

⇒ P² + Q² = R and P² - Q² = R′

⇒ (P² + Q²) / (P² - Q²) = R / R′ = 25 / 7

⇒ P² + Q² = (25/7)(P² - Q²)

⇒ P² + Q² = (25/7)P² - (25/7)Q²

⇒ Multiply through and solve: P/Q = 4/3.

ASSIGNMENT

1. The resultant of two forces 3P and 2P is R. If the first force is doubled, the resultant is also doubled. The angle between the forces if
   (A) π/3 (B) 2π/3 (C) π/6 (D) 5π/6
2. Forces 7, 5 and 3 acting on a particle are in equilibrium, the angle between the pair of forces 5 and 3 is
   (A) 120° (B) 90° (C) 60° (D) 30°
3. The direction of three forces 1N, 2N and 3N acting at a point are parallel to the sides of an equilateral triangle taken in order. The magnitude of their resultant is
   (A) √3/2 N (B) 3N (C) √3 N (D) 3/2 N
4. Two forces A and B such that A : B = 2 : 3. If their resultant R inclined at an angle 60° to A, then angle between R and B is
   (A) sin^-1(1/√2) (B) sin^-1(1/√3) (C) sin^-1(1/2) (D) sin^-1(1/3)
5. Two forces P and Q act at a point and are such that the direction of one is reversed, the resultant is turned through a right angle. Then
   (A) P = 2Q (B) 2P = Q (C) P = Q (D) none of these
6. Two forces acting on a particle are not on a line. If one is doubled and the other is increased by 40N, then the resultant remains unaltered in direction the later force is
   (A) 20 (B) 40 (C) 60 (D) 80
7. Forces P, Q and R acting along OA, OB and OC, where O is the centroid of the equilateral triangle ABC are in equilibrium. Then P : Q : R is
   (A) 1 : √2 : √2 (B) 1 : 1 : 1 (C) √2 : 1 : 2 (D) none of these
8. Two parallel forces not having the same line of action form a couple if they are
   (A) like and unlike (B) like and equal (C) unequal and unlike (D) equal and unlike

ANSWERS TO ASSIGNMENT

1. B

2. A

3. C

4. B

5. C

6. B

7. B

8. D