About Constructions – Class 9 Maths
The class-9 maths notes for the Chapter-Constructions chapter develops essential drawing and geometrical skills. Our class-9 maths notes help students understand the construction of bisectors, triangles, and angles using a compass and ruler. These notes simplify geometric drawing with precise steps and diagrams. The NCERT solutions for class 9 Maths offer accurate guidance to help students replicate each construction perfectly. Our Class 9 Maths tuition gives learners hands-on experience with compass-based activities. Tutors demonstrate each step live, ensuring that students master geometric accuracy and logical reasoning—skills vital for higher classes and exams.
To Construct the Bisector of a Line Segment
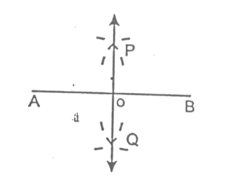
AB = 7.8 cm.
STEPS:
- Draw the line segment AB = 7.8 cm.
- With point A as centre and a suitable radius, more than half the length of AB, draw arcs on both the sides of AB.
- With point B as centre and with the same radius draw arcs on both the sides of AB. Let these arc cut at points P & Q as shown in the figure.
- Draw a line through the points P and Q. The line so obtained is the required perpendicular bisector of given line segment AB.
- (A) PQ bisects AB i.e., OA = OB.
- (B) PQ is perpendicular to AB i.e., ∠PAO = ∠POB = 90°.
Proof:
In ΔAPQ and ΔBPQ:
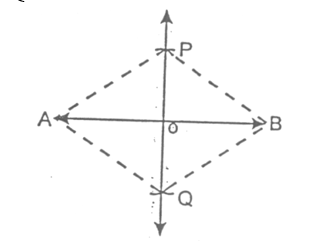
- AP = BP [By construction]
- AQ = BQ [By construction]
- PQ = PQ [Common]
- ∴ ΔAPQ ≅ ΔBPQ [By SSS]
- ∴ ∠APQ = ∠BPQ [By cpctc]
Now, in ΔAPO & ΔBPO:
- AP = BP [By construction]
- OP = OP [Common side]
- ∠APO = ∠BPO [Proved above]
- ∴ ΔAPO ≅ ΔBPO [By SAS]
And, ∠POA = ∠POB
= 180°/2 = 90° [∵ ∠POA + ∠POB = 180°]
∴ PQ is perpendicular bisector of AB.
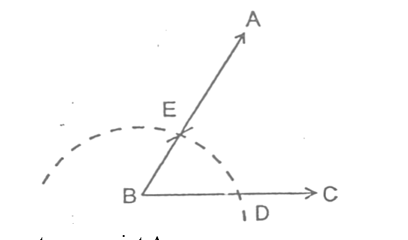
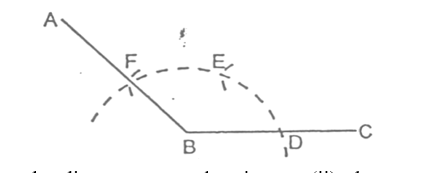
To Construct the bisector of a Given Angle
Let ∠ABC be the given angle to be bisected.
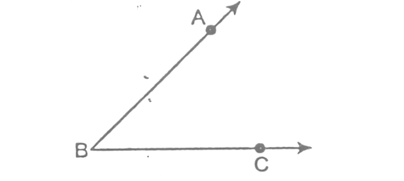
STEPS:
- With B as centre and a suitable radius, draw an arc which cuts ray BA at point D and ray BC at point E.
- Taking D and E as centres and with equal radii draw arcs which intersect each other at point F. In this step, each equal radius must be more than half the length DE.
- Join B and F and produce to get the ray BF.
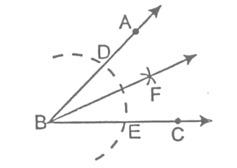
Proof:
Join DF and EF.
In ΔBDF and ΔBEF:
- BD = BE [Radii of the same arc]
- DF = EF [Radii of the equal arcs]
- BF = BF [Common]
- ∴ ΔBDF ≅ ΔBEF [By SSS]
- ∴ ∠DBF = ∠EBF [By cpctc]
i.e., ∠ABF = ∠CBF
∴ BF bisects ∠ABC. Hence Proved.
To Construct the Requires Angle
(a) To Construct the Required Angle of 60°:
STEPS:
- Draw a line BC of any suitable length.
- With B as centre and any suitable radius, draw an arc which cuts BC at point D.
- With D as centre and radius same, as taken in step (ii), draw one more arc which cuts previous arc at point E.
- Join BE and produce upto any point A.
Then, ∠ABC = 60°
(b) To Construct an Angle of 120°:
STEPS:
- Draw a line BC of any suitable length.
- Taking B as centre and with any suitable radius, draw an arc which cuts BC at point D.
- Taking D as centre, draw an arc of the same radius, as taken in step (ii), which cuts the first arc at point E.
- Taking E as centre and radius same, as taken in step (ii), draw one more arc which cuts the first arc at point F.
- Join BF and produce upto any suitable point A.
Then, ∠ABC = 120°
(c) To Construct an Angle of 30°:
STEPS:
- Construct angle ∠ABC = 60° by compass.
- Draw BD, the bisector of angle ∠ABC.
Then, ∠DBC = 30°
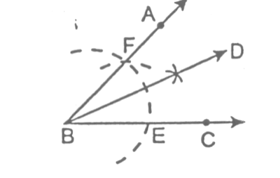
(d) To Construct an Angle of 90°:
STEPS:
- Construct angle ∠ABC = 120° by using compass.
- Draw PB, the bisector of angle ∠EBG.
Then, ∠PBC = 90°
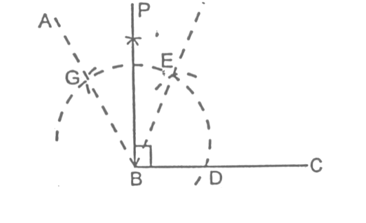
Alternative Method:
- Draw a line segment BC of any suitable length.
- Produce CB upto an arbitrary point O.
- Taking B as centre, draw an arc which cuts OC at points D and E.
- Taking D and E as centres and with equal radii draw arcs which cut each other at point P. (The radii in this step must be of length more than half of DE.)
- Join BP and produce.
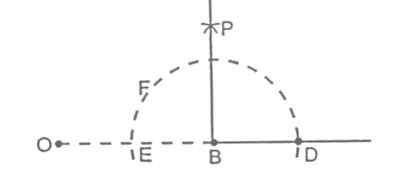

Then, ∠PBC = 90°
(e) To Construct an Angle of 45°:
STEPS:
- Draw ∠PBC = 90°
- Draw AB which bisects angle ∠PBC.
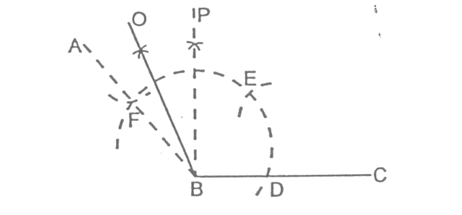
Then, ∠ABC = 45°
Alternative Method:
- Construct ∠ABC = 60°
- Draw BD, the bisector of angle ∠ABC.
- Draw BE, the bisector of angle ∠ABD.
Then, ∠EBC = 45°
(f) To Construct an Angle of 105°:
STEPS:
- Construct ∠ABC = 120° and ∠PBC = 90°
- Draw BO, the bisector of ∠ABP.
Then, ∠OBC = 105°
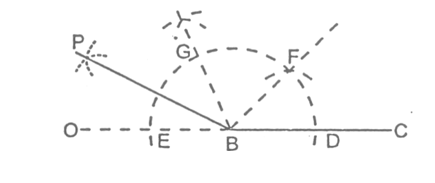
(g) To Construct an Angle of 150°:
STEPS:
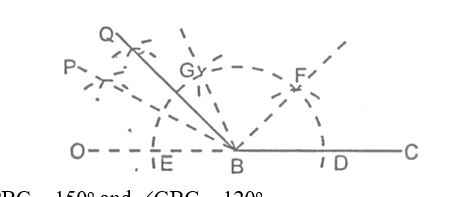
- Draw line segment BC of any suitable length. Produce CB upto any point O.
- With B as centre, draw an arc (with any suitable radius) which cuts OC at points D and E.
- With D as centre, draw an arc of the same radius, as taken in step 2, which cuts the first arc at point F.
- With F as centre, draw one more arc of the same radius, taken in step 2, which cuts the first arc at point G.
- Draw PB, the bisector of angle ∠EBG.
Now ∠FBD = ∠GBF = ∠EBG = 60°
Then, ∠PBC = 150°
(h) To Construct an Angle of 135°:
STEPS:
- Construct ∠PBC = 150° and ∠GBC = 120°
- Construct BQ, the bisector of angle ∠PBG.
Then, ∠QBC = 135°
To Construct a Triangles
Case (i) To construct an equilateral triangle when its one side is given.
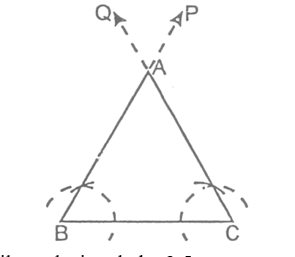
Sol. Given one side of the equilateral triangle be 2.5 cm.
STEPS:
- Draw the line segment BC = 2.5 cm.
- Through B, construct ray BP making angle 60° with BC. i.e. ∠PBC = 60°
- Through C, construct CQ making angle 60° with BC i.e., ∠QCB = 60°
- Let BP and CQ intersect each other at point A.
Then, ΔABC is the required equilateral triangle.
Proof:
Since, ∠ABC = ∠ACB = 60°
∴ ∠BAC = 180° – (60° + 60°) = 60°
∴ All the angles of the ΔABC drawn are equal.
∴ All the sides of the ΔABC drawn are equal.
∴ ΔABC is the required equilateral triangle. Hence Proved.
Alternate method:
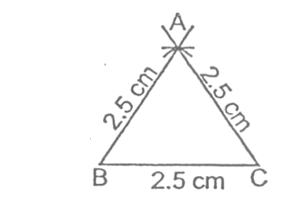
If one side is 2.5 cm, then each side of the required equilateral triangle is 2.5 cm.
- Draw BC = 2.5 cm
- With B as centre, draw an arc of radius 2.5 cm
- With C as centre, draw an arc of radius 2.5 cm
- Let the two arcs intersect each other at point A. Join AB and AC.
Then, ΔABC is the required equilateral triangle.
Case (ii) When the base of the triangle, one base angle and the sum of other two sides are given.

Sol. Given the base BC of the triangle ABC be 3 cm, one base angle ∠B = 60° and the sum of the other two sides be 8 cm i.e., AB + AC = 8 cm.
STEPS:
- Draw BC = 3 cm
- At point B, draw PB so that ∠PBC = 60°
- From BP, cut BD = 8 cm.
- Join D and C.
- Draw perpendicular bisector of CD, which meets BD at point A.
- Join A and C.
Thus, ΔABC is the required triangle.
Proof:
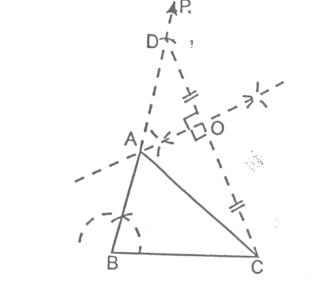
Since, OA is perpendicular bisector of CD
- ∴ OC = OD
- ∠AOC = ∠AOD = 90°
- Also, OA = OA [Common]
- ∴ ΔAOC ≅ ΔAOD [By SAS]
- ∴ AC = AD
∴ BD = BA + AD
= BA + AC
= Given sum of the other two sides
Thus, base BC and ∠B are drawn as given and BD = AC. Hence Proved.

Sol. Here, if we consider the required triangle to be ΔABC, as shown alongside. Clearly, AB = 3.8 cm, ∠B = 90° and BC + AC = 6 cm.
STEPS:
- Draw AB = 3.8 cm
- Through B, draw line BP so that ∠ABP = 90°
- From BP, cut BD = 6 cm
- Join A and D.
- Draw perpendicular bisector of AD, which meets BD at point C.
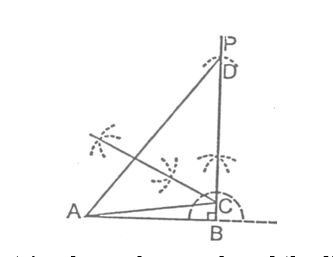
Thus, ΔABC is the required triangle.
Case (iii) When the base of the triangle, one base angle and the difference of the other two sides are given.
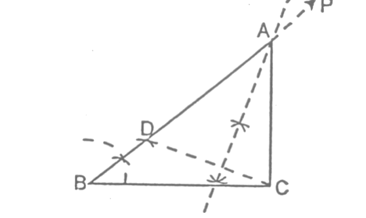
Sol. Given the base BC of the required triangle ABC be 8 cm i.e., BC = 8 cm, base angle ∠B = 60° and the difference between the lengths of other two sides AB and AC be 3 cm.
i.e., AB - AC = 3 cm or AC - AB = 3 cm.
(a) When AB - AC = 3 cm i.e., AB > AC:
STEPS:
- Draw BC = 8 cm
- Through point B, draw BP so that ∠PBC = 60°
- From BP cut BD = 3 cm.
- Join D and C.
- Draw perpendicular bisector of DC; which meets BP at point A.
- Join A and C.
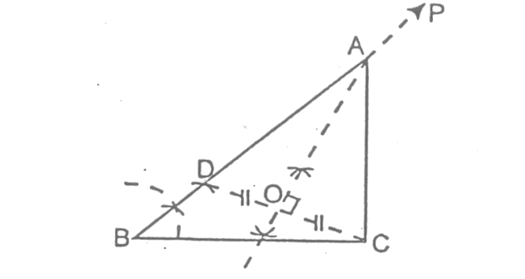
Thus, ΔABC is the required triangle.
Proof:
Since OA is perpendicular bisector of CD
- ∴ OD = OC
- ∠AOD = ∠AOC = 90°
- And, OA = OA [Common]
- ∴ ΔAOD ≅ ΔAOC [By SAS]
- ∴ AD = AC [By cpctc]
Now, BD = BA – AD
= BA – AD
= BA – AC
= Given difference of other two sides.
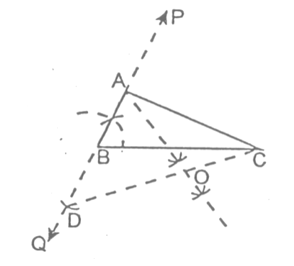
Thus, the base BC and ∠B are drawn as given and BD = BA – AC. Hence Proved.
(b) When AC - AB = 3 cm i.e, AB < AC:
STEPS:
- Draw BC = 8 cm
- Through B, draw line BP so that angle ∠PBC = 60°.
- Produce BP backward upto a suitable point Q.
- From BQ, cut BD = 3 cm.
- Join D and C.
- Draw perpendicular bisector of DC, which meets BP at point A.
- Join A and C.
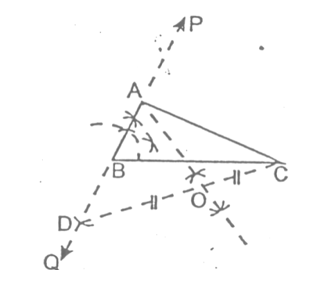
Thus, ΔABC is the required triangle.
Proof:
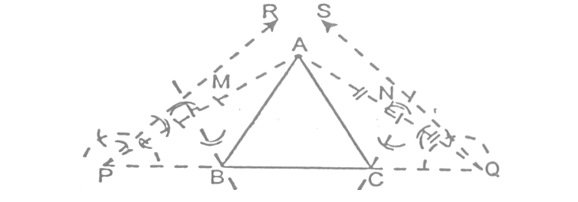
Since, OA is perpendicular bisector of CD
- ∴ OD = OC
- ∠AOD = ∠AOC = 90°
- And OA = OA [Common]
- ∴ ΔAOD ≅ ΔAOC [By SAS]
- ∴ AD = AC [By cpctc]
Now, BD = AD – AB
= AC – AB [∵ AD = AC]
= Given difference of other two sides.
Thus, the base BC and ∠B are drawn as given and BD = AC – AB. Hence Proved.
Case (iv) When the perimeter of the triangle and both the base angles are given:
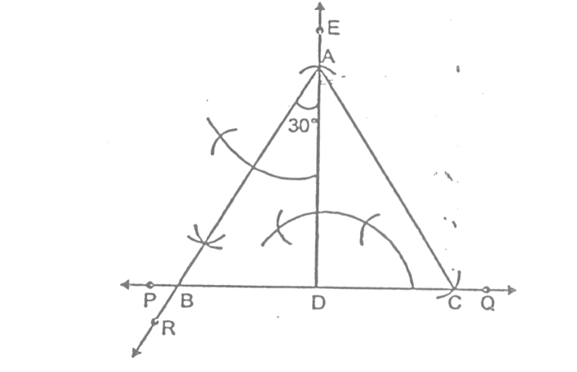
Sol. Given the perimeter of the triangle ABC be 12 cm i.e., AB + BC + CA = 12 cm and both the base angles be 45° and 60° i.e., ∠B = 45° and ∠C = 60°
STEPS:
- Draw a line segment PQ = 12 cm
- At P, construct line PR so that ∠RPO = 45° and at Q, construct a line QS so that ∠SQP = 60°.
- Draw bisector of angles ∠RPQ and ∠SQP which meet each other at point A.
- Draw perpendicular bisector of AP, which meets PQ at point B.
- Draw perpendicular bisector of AQ, which meets PQ at point C.
- Join AB and AC.
Thus, ΔABC is the required triangle.
Proof:
Since, MB is perpendicular bisector of AP
- ∴ ΔQNC ≅ ΔANC [By SAS]
- PB = AC
Similarly, NC is perpendicular bisector of AQ.
- ∴ ΔQNC ≅ ΔANC [By SAS]
- ∴ CQ = AC [By cpctc]
Now, PQ = PB + BC + CQ
= AB + BC + AC
= Given perimeter of the ΔABC drawn.
Also, ∠BPA = ∠BAP [As ΔPMB ≅ ΔAMB]
∴ ∠ABC = ∠BPA + ∠BAP
[Ext. angle of a triangle = sum of two interior opposite angles]
∠ABC = ∠BPA + ∠BAP = 2∠BPA = ∠RPB = ∠ACB [Given]
∠ACB = ∠CQA + ∠CQA
= 2∠CQA [∵ ΔQNC ≅ ΔANC ∴ ∠CQA = ∠CAQ]
= ∠SQC = Given base angle ∠ACB.
Thus, given perimeter = perimeter of ΔABC.
given one base angle = angle ABC
and, given other base angle = angle ACB.
Sol. Given In an equilateral ΔABC an altitude AD = 3.2 cm
Required to Construct an equilateral triangle ΔABC from the given data.
STEPS:
- Draw a line PQ and mark a point D on it.
- Construct a ray DE perpendicular to PQ.
- Cut off DA = 3.2 cm from DE.
- Construct ∠DAR = 30° = (1/2 × 60°). The ray AR intersects PQ at B.
- Cut off line segment DC = BD.
- Join A and C. We get the required ΔABC.
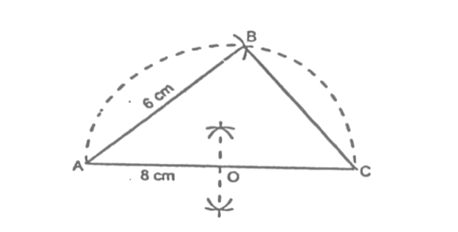
Sol. Given Hypotenuse AC of a ΔABC = 8 cm and one side AB = 6 cm.
Required To construct a right angled ΔABC from the given data.
STEPS:
- Draw a line segment AC = 8 cm.
- Mark the midpoint O of AC.
- With O as centre and radius OA, draw a semicircle on AC.
- With A as centre and radius equal to 6 cm, draw an arc, cutting the semicircle at B.
- Join A and B; B and C. We get the required right angled triangle ABC.
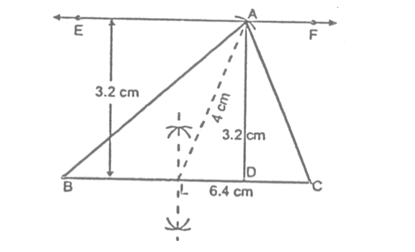
Sol. Given: One side BC = 6.4 cm, Altitude AD = 3.2 cm and the median AL = 4 cm.
Required: To construct a ΔABC from the given data.
STEPS:
- Draw BC = 6.4 cm
- Bisect BC at L.
- Draw EF ∥ BC at a distance 3.2 cm from BC.
- With L as centre and radius equal to 4 cm, draw an arc, cutting EF at A.
- Join A and B; A and C. We get the required triangle ABC.
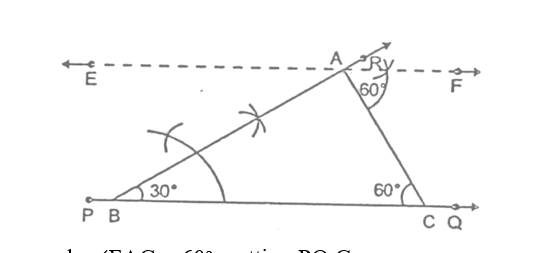
Sol. Given: ∠B = 30°, ∠C = 60°, length of perpendicular from vertex A to the base BC = 4.8 cm.
Required: To construct a ΔABC from the given data.
STEPS:
- Draw any ray line PQ.
- Take a point B on line PQ and construct ∠QBR = 30°
- Draw a line EF ∥ PQ at a distance of 4.8 cm from PQ, cutting BR at A.
- Construct an angle ∠FAC = 60°, cutting PQ at C.
- Join A and C. We get the required triangle ABC.
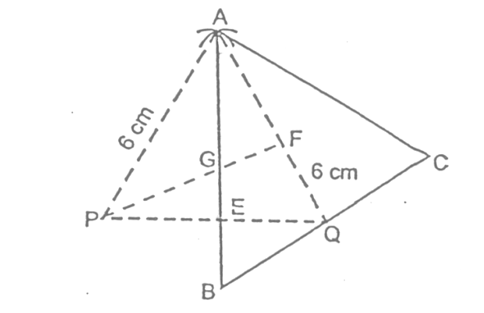
Sol. Given: Median AD = 6 cm, Median BE = 7 cm, Median CF = 6 cm.
Required: To construct a ΔABC from the given data.
STEPS:
- Construct a ΔAPQ with AP = 6 cm, PQ = 7 cm and AQ = 6 cm.
- Draw the medians AE and PF of ΔAPQ intersecting each other at G.
- Produce AE to B such that GE = EB
- Join B and Q and produce it to C, such that BQ = QC
- Join A and C. We get the required triangle ABC.
Key Concepts
- Points lying on the perpendicular bisector of the line segment joining the two points are equidistant from them.
- A triangle is unique if:
- Two sides and the included angle is given.
- Three sides are given.
- Two angles and the included side is given.
- In a right triangle, hypotenuse and one side is given.
- Perimeter of a triangle is equal to sum of its three sides.
- Altitude to a given line segment intersects the line at 90°.
- Median of a line segment bisects the given line segment.
- Perpendicular bisector of a line segment bisects the line segment at right angles.
EXERCISE
For each angle, given below, make a separate construction. Draw a ray BC and another ray BA so that the ∠ABC is equal to:
- 15°
- 22½°
- 75°
- 52½°
- 67½°
- 165°
- 135°
8. Construct an equilateral triangle with side:
- (i) 5 cm
- (ii) 5.4 cm
- (iii) 6.2 cm
9. Construct a triangle ABC, in which:
- (i) base AB = 5.4 cm, ∠B = 45° and AC + BC = 9 cm.
- (ii) base BC = 6 cm, ∠B = 60° and AB + AC = 9.6 cm.
- (iii) base AC = 5 cm, ∠C = 90° and AB + BC = 10.6 cm.
10. Construct a right triangle, with base = 4 cm and the sum of the other side and hypotenuse = 9.4 cm.
11. Construct a triangle ABC, in which:
- (i) BC = 4.8 cm, ∠B = 45° and AB – AC = 2.4 cm.
- (ii) BC = 4.8 cm, ∠B = 45° and AC – AB = 2.4 cm.
- (iii) AB = 5.3 cm, ∠A = 60° and AC – BC = 2 cm.
- (iv) AB = 5.3 cm, ∠A = 60° and BC – AC = 2 cm.
12. Construct a triangle ABC, with:
- (i) perimeter = 12 cm, ∠B = 45° and ∠C = 60°.
- (ii) perimeter = 11.6 cm, ∠B = 60° and ∠C = 90°
- (iii) perimeter = 11 cm, ∠A = 60° and ∠C = 45°.
- (iv) perimeter = 10 cm, ∠B = ∠C = 60°
13. Construct an equilateral triangle with perimeter 15.6 cm.
14. Without finding the length of each side of the equilateral triangle construct it. If its perimeter is 16 cm.
15. Construct an equilateral triangle whose altitude is 4.8 cm.
16. Construct a ΔPQR in which base QR = 4 cm, ∠R = 30° and PR – PQ = 1.1 cm.
17. Construct a ΔXYZ with perimeter 9.6 cm and base angles 30° and 60°.
18. Construct a ΔPQR in which PQ = 3.7 cm, QR = 3.6 cm and median PA = 3.1 cm.
19. Construct a ΔDEF, the lengths of whose medians are 6 cm, 7 cm and 8 cm.
20. Construct an equilateral triangle, one of whose altitudes measures 6.4 cm.