Linear equations in two variables

About Linear Equations in Two Variables – Class 9 Maths

The class-9 maths notes for the Chapter-Linear Equations in Two Variables chapter helps students understand how algebraic relationships are represented graphically. With our Class 9 maths notes, you can easily learn methods to plot equations and interpret graphs. The NCERT solutions for class 9 Maths provide step-by-step problem-solving strategies for each exercise question. Our Class 9 Maths tuition sessions use real-life examples to explain how two-variable equations work, making the concepts practical and engaging. Through guided practice, students learn substitution and elimination methods efficiently, building a strong foundation for future algebraic concepts.

Linear Equations in One Variable

An equation of the form ax + b = 0 where a and b are real numbers and 'x' is a variable, is called a linear equation in one variable.

Here 'a' is called coefficient of x and 'b' is called as a constant term. Examples: 3x + 5 = 0, 7x – 2 = 0 etc.

Linear Equations in Two Variable

An equation of the form ax + by + c = 0 or ax + by = c where a, b, c are real numbers, a ≠ 0, b ≠ 0 and x, y are variables is called a linear equation in two variables.

Any pair of values of x and y which satisfies the equation ax + by + c = 0, a ≠ 0, b ≠ 0 is called a solution of it.

Important Points:

• In the equation ax + by + c = 0, if a = 0, b ≠ 0 or a ≠ 0, b = 0 then the equation reduces to by = c or ax = c. i.e. we get equation in one variable.
• A linear equation in two variables has infinitely many solutions.

Example 1: Prove that x = 3, y = 2 is a solution of 3x - 2y = 5.

Solution: x = 3, y = 2 is a solution of 3x - 2y = 5, because L.H.S. = 3x - 2y = 3 × 3 - 2 × 2 = 9 - 4 = 5 = R.H.S.

i.e. x = 3, y = 2 satisfied the equation 3x - 2y = 5. ∴ it is solution of the given equation.

Example 2: Prove that x = 1, y = 1 as well as x = 2, y = 5 is a solution of 4x - y - 3 = 0.

Solution: Given eq. is 4x - y - 3 = 0 ....(i)

First we put x = 1, y = 1 in L.H.S. of eq...(i) Here L.H.S. = 4x - y - 3 = 4 × 1 - 1 - 3 = 4 - 4 = 0 = R.H.S.

Now we put x = 2, y = 5 in eq. (i) L.H.S. = 4x - y - 3 = 4 × 2 - 5 - 3 = 8 - 8 = 0 = R.H.S.

Since, x = 1, y = 1 and x = 2, y = 5 both pair satisfied in given equation therefore they are the solution of given equation.

Example 3: Solve the equation x/4 + 7 = 19 and verify the answer.

Solution: x/4 + 7 = 19 …(i)

⇒ x/4 = 19 - 7 ⇒ x/4 = 12 ⇒ x = 48

Putting x = 48 in equation (i) we get LHS, x/4 + 7 = 48/4 + 7 = 12 + 7 = 19 R.H.S.

Hence, L.H.S. = R.H.S

Graphical Solution of a Linear Equation

For Equations in One Variable:

In order to draw the graph of a linear equation in one variable we may follow the following algorithm.

Step I: Obtain the linear equation.

Step II: If the equation is of the form ax = b, a ≠ 0, then plot the point (b/a, 0) and one more point (b/a, α) when α is any real number. If the equation is of the form ay = b, a ≠ 0, then plot the point (0, b/a) and (β, b/a) where β is any real number.

Step III: Joint the points plotted in step II to obtain the required line.

Note: If eq. is in form ax = b then we get a line parallel to Y-axis and if eq. is in form ay = b then we get a line parallel to X-axis.

Example 4: Draw the graph of

(i) 2x + 5 = 0(ii) 3y - 15 = 0

Solution:

(i) Graph of 2x + 5 = 0

On simplifying it we get 2x = –5 ⇒ x = –5/2

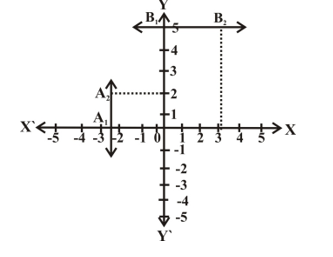
First we plot point A₁(-5/2, 0) & then we plot any other point A₂(-5/2, 2) on the graph paper, then we join these two points we get required line as shown in figure below.

(ii) Graph of 3y - 15 = 0

On simplifying it we get 3y = 15 ⇒ y = 15/3 = 5.

First we plot the point B₁(0, 5) & then we plot any other point B₂(3, 5) on the graph paper, then we join these two points we get required line m as shown in figure.

Note:

(A) A point which lies on the line is a solution of that equation. A point not lying on the line is not a solution of the equation.

(B) In order to draw the graph of a linear equation ax + by + c = 0 may follow the following algorithm.

Step I: Obtain the linear equation ax + by + c = 0.

Step II: Express y in terms of x i.e. y = -(ax + c)/b or x in terms of y i.e. x = -(by + c)/a.

Step III: Put any two or three values for x or y and calculate the corresponding values of y or x respectively from the expression obtained in Step II. Let we get points as (α₁, β₁), (α₂, β₂), (α₃, β₃).

Step IV: Plot the points (α₁, β₁), (α₂, β₂), (α₃, β₃) on graph paper.

Step V: Joint the points marked in step IV to obtain. The line obtained is the graph of the equation ax + by + c = 0.

Example 5: Draw the graph of the line x – 2y = 3, from the graph find the coordinate of the point when

(i) x = – 5 (ii) y = 0

Solution: Here given equation is x - 2y = 3.

Solving it for y we get 2y = x - 3 ⇒ y = (x - 3)/2

Let x = 0, then y = (0 - 3)/2 = -3/2

x = 3, then y = (3 - 3)/2 = 0

x = -2, then y = (-2 - 3)/2 = -5/2

Hence we get

x	0	3	-2
y	-3/2	0	-5/2

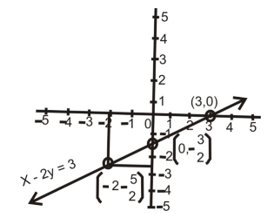
Clearly when x = -5 then y = -4 and when y = 0 then x = 3.

Example 6: Draw the graphs of the lines represented by the equations x + y = 4 and 2x - y = 2 in the same graph. Also find the coordinate of the point where the two lines intersect.

Solution: Given equations are x + y = 4 ......(i) & 2x - y = 2 ......(ii)

(i) We have y = 4 - x

x	0	2	4
y	4	2	0

(ii) We have y = 2x – 2

x	1	0	3
y	0	–2	4

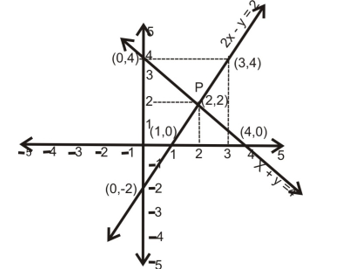
By drawing the lines on a graph paper, clearly we can say that P is the point of intersection where coordinates are x = 2, y = 2.

Different Forms of Line

Slope of a line

If a line makes an angle θ with positive direction of x-axis then tangent of this angle is called the slope of a line, it is denoted by m i.e. m = tan θ.

(i) Slope - intercept form is y = mx + c where m is the slope of line and c is intercept made by line with Y-axis.

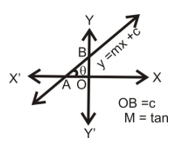
(ii) The equation of a line passing through origin is y = mx. Here c = 0 then the line passes always from origin.

(iii) Intercept form of line is x/a + y/b = 1 where a & b are intercepts on positive direction of x-axis and y-axis respectively made by line.

Solution of Linear Equation in One Variable

Let ax + b = 0 is one equation then ax + b = 0 ⇒ ax = -b ⇒ x = -b/a is a solution.

Example 7: Solve: x/2 = 3 + x/3

Solution: Given x/2 = 3 + x/3

⇒ x/2 - x/3 = 3 ⇒ (3x - 2x)/6 = 3 ⇒ x/6 = 3 ⇒ x = 18

Solution of Linear Equation in Two Variable

By Elimination of Making equal coefficient

Example 8: Solve the following equations

2x – 3y = 53x + 2y = 1

Solution: Given eq. are 2x – 3y = 5 .....(i) 3x + 2y = 1 ....(ii)

Multiplying eq. (i) by 3 and eq. (ii) by 2 we get 6x - 9y = 15 6x + 4y = 2

On subtraction: -9y - 4y = 15 - 2 ⇒ –13y = 13 ⇒ y = 13/(-13) ⇒ y = -1

Put the value of y in eq. (i) we get 2x – (3) × (–1) = 5 2x + 3 = 5 ⇒ 2x = 5 - 3 ⇒ 2x = 2 ⇒ x = 1

∴ x = 1, y = -1

Subsitution Method

Example 9: Solve x + 4y = 14 ....(i) 7x – 3y = 5 ...(ii)

Solution: From equation (i) x = 14 - 4y

Substitute the value of x in equation (ii) ⇒ 7(14 - 4y) - 3y = 5 ⇒ 98 - 28y - 3y = 5 ⇒ 98 - 31y = 5 ⇒ 93 = 31y ⇒ y = 93/31 ⇒ y = 3

Now substitute value of y in equation (ii) ⇒ 7x - 3(3) = 5 ⇒ 7x - 9 = 5 ⇒ 7x = 14 ⇒ x = 14/7 = 2

So, solution is x = 2 and y = 3.

Equations of Lines Parallel to the X-Axis and Y-Axis

On the x-axis, the y-coordinate of each point is 0. In fact, every point on the x-axis is of the form (x, 0). Equation of the x-axis is given by y = 0

On the y-axis, the x-coordinate of each point is 0. In fact, every point on the y-axis is of the form (0, y). Equation of the y-axis is given by x = 0

• y = 0 can be expressed as 0.x + 1.y = 0
• x = 0 can be expressed as 1.x + 0.y = 0

Example: What type of graph x + 4 = 0 and y – 4 = 0 will be?

Solution:

• x + 4 = 0 will be a graph parallel to y-axis.
• y – 4 = 0 will be a graph parallel to x-axis.

Linear Equations in Two Variable - Summary

Key Points:

• An equation of the form ax + by + c = 0 where a, b, c are real numbers, a ≠ 0, b ≠ 0 and x, y are variables is called a linear equation in two variables
• Any pair of values of x and y which satisfies the equation ax + by + c = 0, where a, b, c are non-zero real numbers, is called a solution of the equation.
• If a ≠ 0, c ≠ 0 and b = 0: The equation ax + by + c = 0 reduces to ax + c = 0 or x = -c/a. The graph is a straight line parallel to y-axis and passing through the point (-c/a, 0).
• If b ≠ 0, c ≠ 0 and a ≠ 0: The equation ax + by + c = 0 reduces to by + c = 0 or y = -c/b. The graph is a straight line parallel to x-axis and passing through the point (0, -c/b).
• If a ≠ 0, b ≠ 0, c = 0: The equation ax + by + c = 0 reduces to ax = 0 i.e. x = 0. The graph is y-axis itself
• If a = 0, b ≠ 0, c = 0: The equation ax + by + c = 0 reduces to by = 0 i.e. y = 0. The graph is x-axis itself
• If c = 0, the equation ax + by + c = 0 reduces to ax + by = 0. The graph is a line passing through origin.
• A linear equation in two variables has infinitely many solutions.
• Every point on the graph of a linear equation in two variables is a solution of the equation.

Geometric representation of ax + c = 0 as an equation:

• in one variable is x = -c/a
• in two variable is a.x + 0.y = -c

Pratice Problems - Let's Try

Questions:

Q1. Find two solutions for 3x + 6y = 15.

Q2. Represent the linear equation -2x + 3y - 6 in the form ax + by + c = 0 and determine the values of a, b and c.

Q3. Find the value of k if x = 2, y = 1 is a solution of the equation 2x + 3y = k

Q4. Express x in terms of y, it is being given that 7x - 3y = 15. Check without drawing graph, if the line given by this equation intersects the y-axis at y = -5.

Q5. Draw the graph of the line 3x + y = 6. Find the coordinate of the points at which this line intersects the axes.

Q6. Draw the graph of each of the following linear equation in two variables:

(i) x + y = 4

(ii) y = 3x

(iii) 2x + y = 3

Q7. For each of the graphs given in figure select the equation whose graph it is from choices given below:

(a) (i) x + y = 0 (ii) y = 2x (iii) y = x (iv) y = 2x + 1

(b) (i) x + y = 0 (ii) y = 2x (iii) y = 2x + 4 (iv) y = x - 4

Q8. The taxi fare in a city is as follows. For the first kilometer, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare Rs. y, write a linear equation for this information, and draw its graph.

Answers:

1. (3, 1) and (1, 2)
2. a = -2, b = 3, c = -6
3. k = 7
4. x = (15 + 3y)/7, y₁ = -5
5. x-axis at C(2, 0), y-axis at A(0, 6)
6. Table: x: 1, 2, 3 | y: 8, 13, 18

Illustrations

Q1. The following observed values of x and y are suppose to satisfy the equation y = ax + b. Find the values of a and b.

x	0	1	-1	2	-2
y	3	5	1	7	-1

Solution: Given equations is y = ax + b

Putting x = 1, y = 5 we get 5 = a(1) + b ⇒ 5 = a + b ...(i)

Putting x = -1, y = 1 we get 1 = -a + b ...(ii)

Adding (i) and (ii) ⇒ 5 + 1 = 2b ⇒ 6 = 2b ⇒ b = 6/2 ⇒ 3 = b

Putting the value of b in equation (i) we get ⇒ 5 = a + 3 ⇒ 5 – 3 = a ⇒ 2 = a

Q2. Find solutions of the form x = a, y = 0 and x = 0, y = b for equation 3x + 2y = 6 and 5x - 2y = 10. Does this pair has a common solution?

Solution: The given equations is 3x + 2y = 6

Since, the solution has a form x = a, y = 0 ⇒ 3a + 2(0) = 6 ⇒ 3a = 6 ⇒ a = 6/3 = 2 ∴ (2, 0) is a solution

Also, the solution of the form x = 0, y = b is required ⇒ 3(0) + 2(b) = 6 ⇒ 2b = 6 ⇒ b = 3

∴ (2, 0) and (0, 3) are the two solutions of the first equation

Second equation is 5x - 2y = 10

To get (a, 0) as a solution ⇒ 5(a) - 2(0) = 10 ⇒ 5a = 10 ⇒ a = 10/5 ⇒ a = 2 ∴ (2, 0) is the solution

To get (0, b) as a solution ⇒ 5(0) - 2(b) = 10 ⇒ -2b = 10 ⇒ b = –5 ∴ (0, -5) is the solution

So, (2, 0) and (0, -5) are the two solutions of second equation

(2, 0) is the common solution of both the equations

Q3. Give the equations of four lines passing through (4, 20). How many more such lines are there, and why?

Solution: Equations of four lines passing through (4, 20) are as follows:

• y = 5x or y - 5x = 0
• x + y = 24
• y - x = 16
• 2x - y = -12

In this way many such lines can be drawn because through a given point infinitely many lines can be drawn.

Q4. Find the coordinates of point satisfying equation 2x + 3y = 10, where abscissa and ordinate are equal.

Solution: Given equation 2x + 3y = 10

Let P(x, x) satisfies given equation [∵ x = y] ⇒ 2x + 3x = 10 or 5x = 10 ⇒ x = 2 ∴ y = 2

Coordinates of point satisfying given equation is (2, 2).

Q5. Express, y in terms of x, for equation 3x + 2y = 6. Find the coordinates of a point where 3x + 2y = 6 intersects x axis.

Solution: 2y = 6 - 3x or y = (6 - 3x)/2

Let given line intersects x axis at (x₁, 0) 3x₁ + 2(0) = 6 ⇒ 3x₁ = 6 ⇒ x₁ = 2

Hence given line intersects x-axis at x = 2.

Q6. The taxi fare in a city is as follows. For the first kilometer, the fare is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare Rs. y, write a linear equation for this information, and draw its graph.

Solution: Total distance covered = x km

Also we have fare for 1st km is Rs. 8 and for subsequent distance i.e., (x - 1) km is Rs. 5 per km.

Let the total fare charged = Rs. y

∴ By given condition, we have 8 × 1 + 5(x - 1) = y or 5x – 5 + 8 = y or 5x – y = -3 or y = 5x + 3

Required table is:

x	1	2	3
y	8	13	18

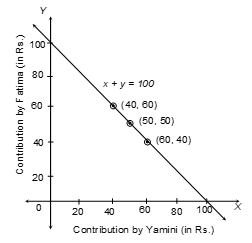
Q7. Yamini and Fatima, two students of class IX of a school, together contributed Rs. 100 towards the prime minister's Relief Fund to help the earthquake victims. Write a linear equation which this data satisfies. Draw the graph of the same.

Solution: Let Rs. x be contributed by Yamini And Rs. y be contributed by Fatima ∴ x + y = 100

Required table is:

x	40	60	50
y	60	40	50

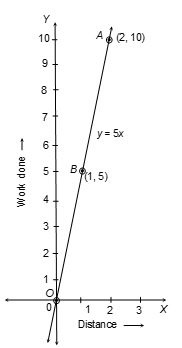
Q8. The work done by a body on application of a constant force is directly proportional to the distance travelled by the body. Express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Read from the graph the work done when the distance travelled by the body is (i) 2 units (ii) 0 units

Solution: Let the work done by a constant force be y = units and the distance travelled by the body be x = units

∴ By given condition, we have y = 5x [∵ 5 is the constant force]

Required table is:

x	0	1	2
y	0	5	10

(i) When distance travelled is 2 units work done is 10 units. [Point A]

(ii) When distance travelled is 0 units work done is also 0 units. [Point O]

Q9. In countries like USA and Canada temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius is: F = (9/5)C + 32

(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis

(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?

(iii) If the temperature is 95°F, what is the temperature in Celsius and if the temperature is 0°F, what is the temperature in Celsius?

(iv) Is there a temperature which is numerically the same in both Fahrenheit and Celsius?

Solution: (i) F = (9/5)C + 32

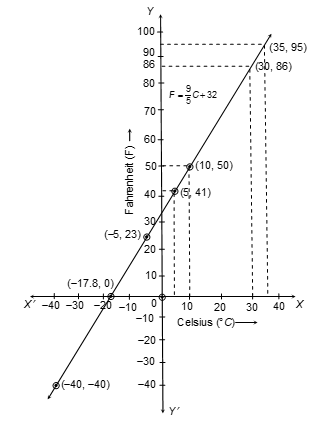
Required table is:

C	5	-5	10
F	41	23	50

The graph of the line F = (9/5)C + 32 is shown in figure

(ii) From the graph: C = 30 ⇒ F = 86

(iii) If F = 95 ⇒ C = 35 on reading the graph. and if F = 0 ⇒ C = -17.8 (approximately)

(iv) Let F = C = x

⇒ x = (9/5)x + 32 [∵ F = (9/5)C + 32] ⇒ x - (9/5)x = 32 ⇒ (4/5)x = -32 ⇒ x = (-32 × 5)/4 ⇒ x = -40°

At -40° both Fahrenheit and Celsius read the same reading.

Q10. Draw the graph of the line y = |x|.

Solution: The given equation y = |x|

By definition of Modulus, we have

y = |x| = { x if x ≥ 0 -x if x < 0 }

Required table is:

Table: y = x

x	0	2	4
y	0	2	4

Table: y = -x

x	0	-2	-4
y	0	2	4

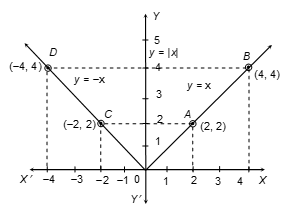
Q11. Solve the equation 2x + 1 = x – 3, and represent the solution(s) on

(i) the number line (in one variable)

(ii) the Cartesian plane (in two variable)

Solution: We solve 2x + 1 = x - 3, to get 2x - x = -3 - 1 i.e., x = -4

(i) The representation of the solution on the number line is shown in figure, where x = -4 is taken as an equation in one variable.

(ii) x = -4 can be written as x + 0.y = -4 which is a linear equation in the variables x and y. This is represented by a line. Graph AB is a line parallel to the y-axis and at a distance of 4 units to the left of it.

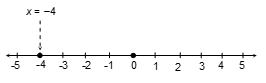
Exercise 1

Ques. The graph of which line is parallel to x-axis

(a) x = 2

(b) y = 2

(c) x + y = 2

(d) none of these

Ques. The graph of which line is parallel to y-axis

(a) x = 2

(b) y = 2

(c) x + y = 2

(d) none of these

Ques. The graph of which line lies in Ist and IIIrd quadrants

(a) 2x + y = 0

(b) x + y = 0

(c) x - y = 0

(d) none of these

Ques. The graph of which line lies in IInd and IVth quadrants.

(a) x + y = 0

(b) x - y = 0

(c) 2x - y = 2

(d) none of these

Ques. The graph of which line is equally inclined to both axes.

(a) 4x - y = 0

(b) 3x - y = 0

(c) 2x - y = 0

(d) x - y = 0

Ques. The graph of which line lies on x-axis

(a) 2x = 0

(b) 2y = 0

(c) 3x = 0 (d) none of these

Ques. The graph of which line lies on y-axis

(a) 2x = 0

(b) 2y = 0

(c) 3y = 0

(d) none of these

Ques. Which line is parallel to x + y = 2.

(a) 2x = 0

(b) y = x + 2

(c) 3x = 0

(d) x = y + 5

Ques. The graph of the line y = |x| lies in

(a) Ist and IIIrd quadrant

(b) Ist and IInd quadrant

(c) IInd and IVth quadrant

(d) none of these

Ques. Which of the line passes through origin (0, 0).

(a) 3x - 4y = 3

(b) y = 2x + 4

(c) y - 2x = 1

(d) y - x = 0

Ques. Which of the point lies on the line 2x + 5y = 13.

(a) (1, 1)

(b) (4, 1)

(c) (-1, 1)

(d) (0, 3)

Ques. Which of the lines is not parallel to other three lines.

(a) y = 2x + 3

(b) y = 2x + 3/2

(c) 3x - y = 0 (d) 2x - y = 0

Ques. If (p, 4) point lies on the line 3x + y = 10, then value of p is

(a) 5

(b) 1

(c) 3

(d) 2

Ques. If expressions 2x - 20 and 48 - 2x are equal then value of x is

(a) 17

(b) 15

(c) 16

(d) 20

Ques. If x = 1, y = 1 is a solution of equation 5x + ky = 11, then value of k is

(a) 1

(b) 11

(c) 6

(d) 5

Ques. A linear equation in two variables ax + by + c = 0, has

(a) one solution

(b) many solutions

(c) no solution

(d) none of these

Ques. Which one is a linear equation:

(a) x(x + 5) = -x(3 - x) + 7

(b) (x - 1)(x - 2) = 5

(c) x + 2/x = 1

(d) none of these

Ques. Which of the following line does not pass through origin (0, 0):

(a) x + y = 0

(b) x - y = 0

(c) x + 2y = 0

(d) y = x + 1

Ques. For each value of x, which of the following equation has same ordinate:

(a) 2y + 5 = 0

(b) 2x + 5 = 0

(c) 2x - 5 = 0

(d) 2x + 3y = 1

Ques. Which of the following is the alternative representation of the equation 2x + 9 = 0

(a) 3x = -9

(b) 0.x + 2y + 9 = 0

(c) 2x + 0.y = -9

(d) 2x + 0.y = 9

Ques. Which of the following equation is not linear equation?

(a) 2x + 3 = 7x - 2

(b) (2/3)x + 5 = 3x - 4

(c) x² + 3 = 5x - 3

(d) (x - 2)² = x² + 8

Ques. Solution of equation √3x - 2 = 2√3 + 4 is

(a) 2(√3 - 1)

(b) 2(1 - √3)

(c) 1 + √3

(d) 2(1 + √3)

Ques. The value of x which satisfy (2x + 6)/(3x + 5) = (4x + 7)/(6x + 5) is

(a) -1

(b) 1

(c) 2

(d) -2

Ques. Solution of (x - a)/(b + c) + (x - b)/(c + a) + (x - c)/(a + b) = 3 is

(a) a + b - c

(b) a - b + c

(c) -a + b + c

(d) a + b + c

Ques. A man is thrice as old as his son. After 14 years, the man will be twice as old as his son, then present age of this son.

(a) 42 years

(b) 14 years

(c) 12 years

(d) 36 years

Ques. One fourth of one third of one half of a number is 12, then number is

(a) 284

(b) 286

(c) 288

(d) 290

Ques. A linear equation in two variables has maximum

(a) only one solution

(b) two solution

(c) infinite solution

(d) None of these

Ques. Solution of the equation x - 2y = 2 is/are

(a) x = 4, y = 1

(b) x = 2, y = 0

(c) x = 6, y = 2

(d) All of these

Ques. The graph of line 5x + 3y = 4 cuts Y-axis at the point

(a) (0, 4/3)

(b) (0, 3/4)

(c) (4/5, 0)

(d) (5/4, 0)

Ques. If x = 1, y = 1 is a solution of equation 9ax + 12ay = 63 then, the value of a is

(a) -3

(b) 3

(c) 7

(d) 5

Answers to Exercise 1

1.	(b)	2.	(a)	3.	(c)	4.	(a)	5.	(d)
6.	(b)	7.	(a)	8.	(c)	9.	(b)	10.	(d)
11.	(b)	12.	(c)	13.	(d)	14.	(a)	15.	(c)
16.	(b)	17.	(a)	18.	(d)	19.	(a)	20.	(c)
21.	(c)	22.	(d)	23.	(b)	24.	(d)	25.	(b)
26.	(c)	27.	(c)	28.	(d)	29.	(a)	30.	(b)

Exercise 2

Ques. If x is the number of hours a labourer is on work and y is his wages in rupees, then y = 4x + 13. Draw the work-wages graph. From your graph find the wages of a labourer who puts in 6 hours of work.

Ques. If x/2 + x/3 - x/4 + x/5 = 47/6, find when y/2 + y/3 - y/4 + y/5 = 47x.

Ques. Verify which of the following are solutions of the equation x - 2y = 4 and which are not: (0, -2), (2, 0), (4, 0), (6, 1), (√2, 4√2), (3, -1/2)

Ques. Find the value of b if (-3, 4) is a solution of the equation 3x - 4y = b.

Ques. Express y in terms of x in the equation 5y - 3x - 10 = 0 Find the point where the line represented by the equation 5y - 3x = 10 cuts the y-axis.

Ques. Express x in terms of y in the equation 3x + 2y = 12 Find the point where the line represented by the equation 3x + 2y - 12 = 0 cuts the x-axis.

Ques. Give the geometrical representation of the equation y = 2 as an equation in (i) one variable (ii) two variables

Ques. Give the geometrical representation of the equation 2x + 7 = 0 as an equation in (i) one variable (ii) two variables

Ques. A man is driving his Esteem Car with a uniform speed of 90 km per hour. Draw the time distance graph. From graph, find the distance travelled by him in (i) 1/2 hour (ii) 2½ hours

Ques. Nidhi and Nisha together contributed Rs 300 towards P.M's Relief fund to help the Tsunami victims. Express the information in the form of a linear equation in two variables and draw the graph of this linear equation.

Ques. If (2x + 7)/(x + 2) = (4x + 3)/(2x - 7), find the value of x³ + x² + x + 1.

Ques. Determine whether x = 5, y = 4 is a solution of the equation x – 2y = –3

Ques. Solve the following linear equations in two variable.

1. 8x – 5y = 34, 3x – 2y = 13
2. 20x + 3y = 7, 8y – 15x = 5
3. 2x - 3y - 3 = 0, (2x/3) + 4y + (1/2) = 0

Answers to Exercise 2

1. Rs. 37
2. 600
3. (0, -2), (4, 0), (6, 1), (3, -1/2)
4. b = -25
5. y = (3/5)x + 2; (0, 2)
6. x = (-2/3)y + 4; (4, 0)
7. (i) 45 km (ii) 225 km
8. x + y = 300 where x and y are their contributions.
9. -104
10. Yes
11. x = 3, y = -2
12. x = 1/5, y = 1
13. x = 21/20, y = -3/10

Exercise 3

Ques. Draw the graph of 2x + 3y = 6 and use it to find the area of triangle formed by the line and co-ordinate axis.

Ques. Draw the graph of the lines 4x – y = 5 and 5y – 4x = 7 on the same graph paper and find the coordinates of their point of intersection.

Ques. Find two numbers such that five times the greater exceeds four times the lesser by 22 and three times the greater together with seven times the lesser is 32.

Ques. Draw the graph of x - y + 1 = 0 and 3x + 2y - 12 = 0 on the same graph. Calculate the area bounded by these lines & X-axis.

Ques. If p = 3x + 1, q = (1/3)(9x + 13) and p : q = 6 : 5 then find x.

Answers to Exercise 3

1. Area = 3 sq. units
2. x = 2, y = 3
3. 6, 2
4. 7.5 sq. units
5. -7