About Triangles – Class 9 Maths
The Triangles chapter is one of the most important parts of Class 9 geometry, helping students understand the properties, congruence, and inequalities of triangles. Our class-9 maths notes make this topic simple and engaging by explaining each concept through clear examples and diagrams. Students can easily learn about congruence criteria such as SSS, SAS, ASA, AAS, and RHS, which are essential for problem-solving and geometric reasoning. For complete conceptual clarity, our NCERT solutions for class 9 Maths provide detailed, step-by-step answers to every question from the textbook. These solutions help students understand how to apply congruence rules and prove geometric theorems efficiently. Each exercise is solved with accuracy, ensuring that learners build a strong foundation for higher classes where geometry becomes even more advanced.
To make learning more effective, our Class 9 Maths tuition focuses on interactive explanations, regular practice sessions, and personalized doubt-clearing. Tutors guide students through important theorems like the “Angle Sum Property of a Triangle,” “Inequalities in a Triangle,” and “Theorem on Proportionality.” Visual tools and real-life examples make geometry enjoyable, ensuring that even complex proofs feel easy and logical.
By combining well-structured class-9 maths notes, accurate NCERT solutions for class 9 Maths, and expert Class 9 Maths tuition, students can gain deep confidence in solving geometry-based problems. Regular practice and conceptual understanding of triangles not only improve board exam performance but also build a strong base for future mathematical learning, especially in coordinate geometry and trigonometry.
At Home-Tution.com, students receive quality resources and one-on-one guidance to master the Triangles chapter effectively. Our notes, solutions, and tuition methods are designed to make every learner excel in understanding geometry through clarity, practice, and precision.
1. Triangle Definition
If ABC is any triangle then:
- Sides: AB, BC & CA are three sides
- Angles: ∠A, ∠B and ∠C are three angles
2. Types of Triangles
(i) On the basis of sides:
(A) Scalene Triangle:
A triangle whose no two sides are equal is called a scalene triangle.
(B) Isosceles Triangle:
A triangle having two sides equal is called an isosceles triangle.
(C) Equilateral Triangle:
A triangle in which all sides are equal is called an equilateral triangle.
(ii) On the basis of angles:
(A) Right Triangle:
A triangle in which any one angle is right angle (=90°) is called right triangle.
(B) Acute Triangle:
A triangle in which all angles are acute (>90°) is called an acute triangle.
(C) Obtuse Triangle:
A triangle in which any one angle is obtuse (<90°) is called an obtuse triangle.
3. Congruent Figures
The figures are called congruent if they have same shape and same size. In other words, two figures are called congruent if they are having equal length, width and height.

(a) Congruent Triangles:
Two triangles are congruent if and only if one of them can be made to superimposed on the other, so to cover it exactly.
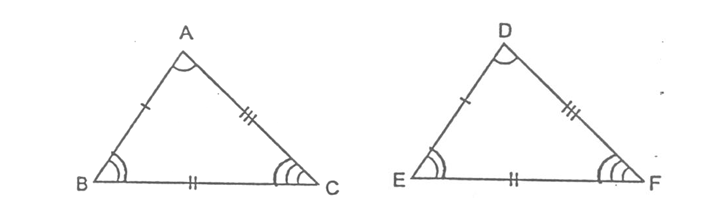
If two triangles ABC and DEF are congruent then there exist a one to one correspondence between their vertices and sides. i.e. we get following six equalities:
∠A = ∠D, ∠B = ∠E, ∠C = ∠F and AB = DE, BC = EF, AC = DF
Notation: If two ΔABC & ΔDEF are congruent under A ↔ D, B ↔ E, C ↔ F one to one correspondence then we write ΔABC ≅ ΔDEF
We cannot write as ΔABC ≅ ΔDFE of ΔABC ≅ ΔEDF or in other forms because ΔABC ≅ ΔDFE have following one-one correspondence A ↔ D, B ↔ F, C ↔ E.
Two triangles are congruent if and only if there exists a one-one correspondence between their vertices such that the corresponding sides and the corresponding angles of the two triangles are equal.
4. Sufficient Conditions for Congruence of Two Triangles
SAS Congruence Criterion (Side-Angle-Side):
Statement: Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of the other triangle.
Example 1:
Given: O is the mid-point of AB and CD.

To Prove:
- ΔAOC ≅ ΔBOD
- AC = BD
- AC || BD
Solution: In Δs AOC and BOD, we have
- AO = OB [∵ O is the mid-point of AB]
- ∠AOC = ∠BOD [Vertically opposite angles]
- CO = OD [∵ O is the mid-point of CD]
So, by SAS congruence criterion, we have ΔAOC ≅ ΔBOD
⇒ AC = BD and ∠CAO = ∠DBO [Corresponding parts of congruent triangles are equal]
Now, AC and BD are two lines intersected by a transversal AB such that ∠CAO = ∠DBO, i.e. alternate angles are equal. Therefore, AC || BD
ASA Congruence Criterion (Angle-Side-Angle):
Statement: Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
Given: Two Δs ABC and DEF such that ∠B = ∠E, ∠C = ∠F and BC = EF
To prove: ΔABC ≅ ΔDEF
Proof: There are three possibilities
Case I: When AB = DE:
In this case, we have AB = DE, ∠B = ∠E, and BC = EF
So, by SAS criterion of congruence, we have ΔABC ≅ ΔDEF
Case II: When BA < ED
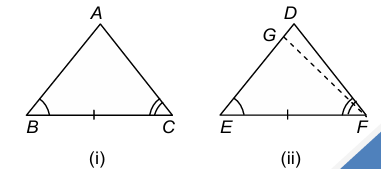
In this case take a point G on ED such that EG = BA. Join GF.
Now, in Δs ABC and GEF, we have:
- BA = GE [Assumed]
- ∠B = ∠E [Given]
- BC = EF [Given]
So, by SAS criterion of congruence, we have ΔABC ≅ ΔGEF
⇒ ∠ACB = ∠GFE [cpct]
But, ∠ACB = ∠DFE [Given]
∴ ∠GFE = ∠DFE
This is possible only when ray FG coincides with ray FD or G coincides with D. Therefore, BA must be equal to ED.
Thus, in Δs ABC and DEF, we have AB = DE [As proved above], ∠B = ∠E [Given], and BC = EF [Given]
So, by SAS criterion of congruence, we have ΔABC ≅ ΔDEF
Case III: when BA > ED
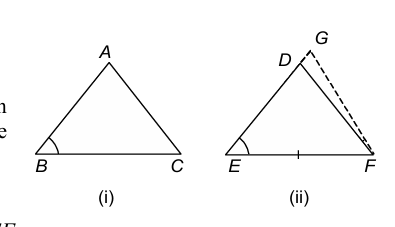
In this case take a point G on ED produced such that EG = BA. Join GF. Now, proceeding as in case II, we prove that ΔABC ≅ ΔDEF
Hence, in all the three cases, we have ΔABC ≅ ΔDEF
AAS Congruence Criterion (Angle-Angle-Side):
Statement: If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
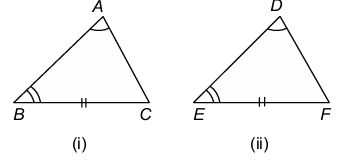
Given: Two Δs ABC and DEF such that ∠A = ∠D, ∠B = ∠E, BC = EF
To prove: ΔABC ≅ ΔDEF
Proof: We have, ∠A = ∠D, and ∠B = ∠E
- ⇒ ∠A + ∠B = ∠D + ∠E
- ⇒ 180° − ∠C = 180° − ∠F [Angle sum property]
- ⇒ ∠C = ∠F ...(i)
Thus, in Δs ABC and DEF, we have: ∠A = ∠D, ∠B = ∠E and ∠C = ∠F
Now, in ΔABC and ΔDEF, we have:
- ∠B = ∠E [Given]
- BC = EF [Given]
- ∠C = ∠F [From (i)]
So, by ASA criterion of congruence, ΔABC ≅ ΔDEF
SSS Congruence Criterion (Side-Side-Side):
Statement: Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle.
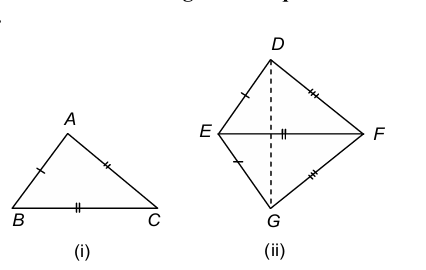
Given: Two Δs ABC and DEF such that AB = DE, BC = EF and AC = DF.
To prove: ΔABC ≅ ΔDEF
Construction: Suppose BC is the longest side. Draw EG such that ∠FEG = ∠ABC and EG = AB. Join GF and GD.
Proof: In Δs ABC and ΔGEF, we have:
- BC = EF [Given]
- AB = GE [By construction]
- ∠ABC = ∠FEG [By construction]
So, by SAS criterion of congruence, we have ΔABC ≅ ΔGEF
⇒ ∠A = ∠G and AC = GF [c.p.c.t.]
Now, AB = DE and AB = GE ⇒ DE = GE
Similarly, AC = DF and AC = GF ⇒ DF = GF
In ΔEGD, we have: DE = GE [From above]
⇒ ∠EDG = ∠EGD [Angles opp. to equal side]
In ΔFGD, we have: DF = GF [From above]
⇒ ∠FDG = ∠FGD [Angles opp. to equal side]
Adding the above two equations:
∠EDG + ∠FDG = ∠EGD + ∠FGD
∴ ∠D = ∠G
But, ∠G = ∠A [Proved above] ∴ ∠A = ∠D
Thus, in Δs ABC and DEF, we have:
- AB = DE [Given]
- ∠A = ∠D [From above]
- AC = DF [Given]
So, by SAS criterion of congruence, we have ΔABC ≅ ΔDEF
RHS Congruence Criterion (Right Angle-Hypotenuse-Side):
Statement: Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle.
Given: Two right angles ABC and DEF in which ∠B = ∠E = 90°, AC = DF, BC = EF
To prove: ΔABC ≅ ΔDEF
Construction: Produce DE to G so that EG = AB. Join GF
Proof: In Δs ABC and ΔGEF, we have:
- AB = GE [By construction]
- ∠ABC = ∠FEG [Both 90°]
- BC = EF [Given]
So, by SAS criterion of congruence, we have ΔABC ≅ ΔGEF
⇒ ∠A = ∠G ...(i) and AC = GF [cpct] ...(ii)
Now, AC = GF [From (ii)] and AC = DF [Given] ∴ DF = GF
⇒ ∠D = ∠G [Angles opposite to equal sides] ...(iii)
From (i) and (iii), we get ∠A = ∠D ...(iv)
Thus, in Δs ABC and DEF, we have:
- ∠A = ∠D [From (iv)]
- ∠B = ∠E [Both 90°]
- ⇒ ∠A + ∠B = ∠D + ∠E
- ⇒ 180° − ∠C = 180° − ∠F [Angle sum property]
- ⇒ ∠C = ∠F ...(v)
Now, in Δs ABC and DEF, we have:
- BC = EF [Given]
- ∠C = ∠F [From (v)]
- AC = DF
So, by SAS criterion of congruence, we have ΔABC ≅ ΔDEF
5. Important Theorems on Triangles
THEOREM 1:
Statement: Angles opposite to equal sides of an isosceles triangle are equal.
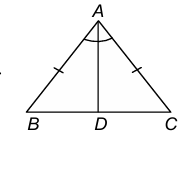
Given: An isosceles triangle ABC in which AB = AC.
To prove: ∠B = ∠C.
Construction: Draw the bisector of ∠A and let D be the point of intersection of this bisector of ∠A and BC.
Proof: In ΔBAD and ΔCAD
- AB = AC [Given]
- ∠BAD = ∠CAD [By construction]
- AD = AD [Common]
ΔBAD ≅ ΔCAD [By SAS Congruency]
∴ ∠ABD = ∠ACD [cpct]
∴ ∠B = ∠C
THEOREM 2:
Statement: If two angles of a triangle are equal, then sides opposite to them are also equal.
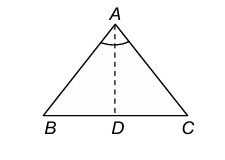
Given: Δ ABC in which ∠B = ∠C
To prove: AC = AB
Construction: Draw the bisector of ∠A and let it meet BC at D.
Proof: In Δs ABD and ACD, we have:
- ∠B = ∠C [Given]
- ∠BAD = ∠CAD [By construction]
- AD = AD [Common]
So, by SAS criterion of congruence, we have ΔABD ≅ ΔACD
⇒ AB = AC [cpct]
Hence, ΔABC is isosceles.
THEOREM 3:
Statement: The sum of any two sides of a triangle is greater than the third side.
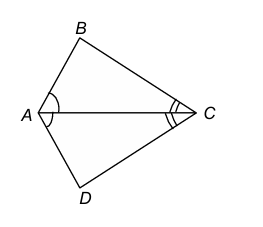
Given: Δ ABC
To prove: AB + AC > BC, AB + BC > AC and BC + AC > AB
Construction: Extend side BA to D such that AD = AC. Join CD
Proof: In ΔACD, we have:
- AC = AD [By construction]
- ⇒ ∠ADC = ∠ACD [Angles opp. to equal sides are equal]
- ⇒ ∠ACD = ∠ADC
∴ ∠BCA + ∠ACD > ∠ADC [∵ ∠BCA + ∠ACD > ∠ACD]
⇒ ∠BCD > ∠ADC
⇒ ∠BCD > ∠BDC [∵ ∠ADC = ∠BDC]
⇒ BD > BC [∵ Side opp. to greater angle is larger]
⇒ BA + AD > BC
⇒ BA + AC > BC [∵ AC = AD (By construction)]
⇒ AB + AC > BC
Thus, AB + AC > BC
Similarly, AB + BC > AC and BC + AC > AB
6. Some Inequality Relations in a Triangle
Inequality Relation 1:
Statement: If two sides of a triangle are unequal, the longer side has greater angle opposite to it.
Given: Δ ABC in which AC > AB
To prove: ∠ABC > ∠ACB
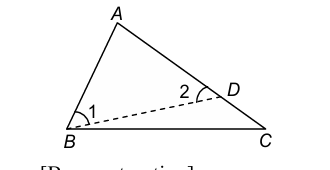
Construction: Mark a point D on AC such that AB = AD. Join BD.
Proof: In ΔABD, we have:
- AB = AD [By construction]
- ⇒ ∠1 = ∠2 [∵ Angles opp. to equal sides are equal] ...(i)
∠2 is the exterior angle of ΔBCD and an exterior angle is always greater than interior opposite angle. Therefore,
∠2 > ∠DCB
⇒ ∠2 > ∠ACB [∵ ∠ACB = ∠DCB] ...(ii)
From (i) and (ii), we have:
⇒ ∠1 > ∠ACB ...(iii)
∵ ∠ABC > ∠1 ...(iv)
From (iii) and (iv), we get ∠ABC > ∠ACB
Inequality Relation 2:
Statement: In a triangle the greater angle has the longer side opposite to it.
Given: Δ ABC in which ∠ABC > ∠ACB
To prove: AC > AB
Proof: In ΔABC, we have the following three possibilities:
- AC = AB
- AC < AB
- AC > AB

Case I: When AC = AB
If AC = AB ⇒ ∠ABC = ∠ACB [Angle opp. to equal sides are equal]
This is a contradiction, Since ∠ABC > ∠ACB [Given]
∴ AC ≠ AB
Case II: When AC < AB
if AC < AB ⇒ ∠ACB > ∠ABC [∵ Longer sides has the greater angle opposite to it]
This is also a contradiction
∴ We are left with the only possibility, AC > AB, which must be true
Hence, AC > AB
7. Solved Examples (Illustrations)
Example 1:
Question: Prove that ΔABC is isosceles if any one of the following holds:
- Altitude AD bisects BC
- Median AD is perpendicular to the base BC
Solution (i):
Let ΔABC be a triangle and let AD, be altitude from A to BC. Suppose D bisects BC i.e. BD = CD. We have to prove that the ΔABC is isosceles.
In ΔADB and ΔADC, we have:
- AD = AD [Common side]
- ∠ADB = ∠ADC [Each equal to 90°]
- BD = DC [Given]
So, by SAS criterion of congruence, we have ΔADB ≅ ΔADC
⇒ AB = AC [cpct]
Hence, ΔABC is isosceles.
Solution (ii):
Let ΔABC be a triangle such that the median AD perpendicular to the base BC.
In Δs ADB and ADC, we have:
- AD = AD [Common side]
- ∠ADB = ∠ADC [Both 90°]
- BD = DC [∵ AD is the median ∴ D is the mid-point of BC]
So, by SAS criterion of congruence, we have ΔADB ≅ ΔADC
⇒ AB = AC [cpct]
Hence, ΔABC is isosceles.
Example 2:
Question: In figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Solution:
We have, ∠PQT = ∠RQU and ∠TQS = ∠UQS
⇒ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS ...(i)
Thus, in triangles PQS and RQS, we have:
- PQ = RQ [Given]
- ∠PQS = ∠RQS [From (i)]
- QS = QS [Common side]
Therefore, by SAS congruence criterion, we have ΔPQS ≅ ΔRQS
⇒ ∠QPS = ∠QRS [cpct]
⇒ ∠QPT = ∠QRU ...(ii)
In Δs PQT and RQU we have:
- QP = QR [Given]
- ∠PQT = ∠RQU [Given]
- ∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we have ΔQPT ≅ ΔQRU
⇒ QT = QU [cpct]
Note: Multiple other solved examples are available in the original document pages 23-34. Due to space constraints, only key examples are shown here. Students should refer to the complete document for all 24 illustrated examples.
8. Let's Try - Practice Problems
Practice Questions:
1. Prove that measure of each angle of an equilateral triangle is 60°.
2. If D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD = ½AC.
3. In a right angled triangle, one acute angle is double the other. Prove that the hypotenuse is double the smallest side.
4. In figure, two sides AB and BC and the median AM of a ΔABC are respectively equal to sides DE and EF and the median DN of ΔDEF. Prove that ΔABC ≅ ΔDEF.
5. In figure, PQ = PR, show that PS > PQ.
6. In figure, T is a point on side QR of ΔPQR and S is a point such that RT = ST. Prove that PQ + PR > QS.
7. Suppose line segments AB and CD intersect at O in such a way that AO = OD and OB = OC. Prove that AC = BD but AC may not be parallel to BD.
9. Exercise - 1 (Multiple Choice Questions)
1. In the three altitudes of a Δ are equal then triangle is:
(a) isosceles
(b) equilateral
(c) right angled
(d) none
2. ABCD is a square and P, Q, R are points on AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°, then ∠QPR
(a) 45°
(b) 50°
(c) 60°
(d) LM
3. In a ΔXYZ, LM ║ YZ and bisectors YN and ZN of ∠Y & ∠Z respectively meet at N on LM then YL + ZM =
(a) YZ
(b) XY
(c) XZ
(d) LM
4. In a ΔPQR, PS is bisector of ∠P and ∠Q = 70° ∠R = 30°, then
(a) QS > PQ > PR
(b) QS < PQ < PR
(c) PQ > QS > SR
(d) PQ < QS < SR
5. If D is any point on the side BC of a ΔABC, then:
(a) AB + BC + CA > 2AD
(b) AB + BC + CA < 2AD
(c) AB + BC + CA > 3AD
(d) None
6. For given figure, which one is correct:
(a) ΔABC ≅ ΔDEF
(b) ΔABC ≅ ΔFED
(c) ΔABC ≅ ΔDFE
(d) ΔABC ≅ ΔEDF
7. In a right angled triangle. One acute angle is double the other then the hypotenuse is:
(a) Equal to smallest side
(b) Double the smallest side
(c) Triple the smallest side
(d) None of these
8. Measure of each angle of an equilateral triangle is
(a) 45°
(b) 60°
(c) 90°
(d) 30°
9. Each exterior angle of an equilateral triangle is
(a) 60°
(b) 90°
(c) 120°
(d) 150°
10. In ΔABC, if ∠A = ∠C then AB = _____.
(a) BC
(b) AC
(c) AB
(d) none of these
11. Perimeter of triangle is ______ sum of its altitudes.
(a) less than
(b) equal to
(c) more than
(d) none of these
12. The sum of any two sides of a triangle is ______ third side.
(a) more than
(b) equal to
(c) less than
(d) none of these
13. The sum of three altitudes of a triangle is _____ its perimeter
(a) more than
(b) equal to
(c) less than
(d) none of these
14. Difference of any two sides of a triangles is ______ third side.
(a) more than
(b) less than
(c) equal to
(d) none of these
15. In ΔABC if AB = AC then altitude BD _______ altitude CE.
(a) greater than
(b) equal to
(c) less than
(d) none of these
16. If the bisector of an angle of a triangle bisects the opposite side then the triangle is
(a) scalene
(b) equilateral
(c) isosceles
(d) right triangle
17. Sum of exterior angle (a + b + c + d + e) of a regular pentagon is
(a) 120°
(b) 180°
(c) 240°
(d) 360°
18. Longest side in right triangle is
(a) perpendicular
(b) base
(c) hypotenuse
(d) none of these
19. In figure AB = AC and DB = DC. Ratio of ∠ABD : ∠ACD is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) none of these
20. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Measures of ∠B and ∠C will be
(a) 60°, 30°
(b) 30°, 60°
(c) 45°, 45°
(d) none of these
Answer Key:
| Q. No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Answer | (b) | (a) | (d) | (b) | (a) | (c) | (b) | (b) | (c) | (a) |
| Q. No. | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| Answer | (c) | (a) | (c) | (b) | (b) | (c) | (d) | (c) | (c) | (c) |
10. Exercise - 2 (Subjective Questions)
Long Answer Type Questions:
1. Show that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle.
2. ABC is a triangle in which ∠B = 2∠C. D is a point on BC such that AD bisect ∠BAC and AB = CD. Prove that ∠BAC = 72°.
3. Show that the difference of any two sides of a triangle is less than the third side.
4. In figure, AD is a median of ΔABC. Prove that AB + AC > 2AD.
OR
Prove that any two sides of a triangle are together greater than twice the median drawn to the third side.
5. In ΔABC, the medians AD, BE and CF intersect at the point G. Show that 2(BE + CF) > 3BC.
6. On the arms PR and RQ of an ∠PRQ, points N and M are taken respectively such that ∠MPR = ∠NQR. If PR = QR, then prove that RM = RN.
7. In the figure, the line segment joining the mid-point M and N of opposite sides AB and DC of quadrilateral ABCD is perpendicular to both sides. Prove that the other sides of the quadrilateral are equal.
8. Prove that sum of the angles of a hexagon is 720°.
9. Prove that the sum of the three sides of a triangle is greater than the sum of its three medians.
10. In the ΔABC given below, BD bisects ∠B and is perpendicular to AC. If the lengths of the sides of the triangle are expressed in terms of x and y as shown, find the values of x and y.
11. In the figure, AB = AD prove that ∠BCD is a right angle.
12. If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
13. AD is median of ΔABC. Prove that AB + AC > 2AD.
14. O is any point in the interior of a triangle ABC. Prove that OB + OC < AB + AC.
15. In figure, ABC is a right angled triangle at B. ADEC and BCFG are squares. Prove that AF = BE.
16. In figure CD is the diameter perpendicular to the chord AB of a circle with centre O. Prove that:
(a) ∠CAO = ∠CBO
(b) ∠AOB = 2∠ACB
17. ABCD is a square and EF║BD. E and F are the mid-point of BC and DC respectively. Prove that:
(a) BE = DF
(b) AR bisects ∠BAD
18. In figure, ΔABC is an equilateral triangle PQ║AC and AC is produced to R such that CR = PQ. Prove that QR bisects PC.
19. In figure, the congruent parts of triangles have been indicated by line markings. Find the values of x & y.