Lines and angles

About Lines and Angles – Class 9 Maths

The class-9 maths notes for the Chapter-Lines and Angles chapter teaches students about different types of angles and relationships between lines. Our Class 9 maths notes explain key concepts like complementary, supplementary, and vertically opposite angles in an easy way. The NCERT solutions for class 9 Maths include detailed explanations of theorems and exercise solutions for thorough understanding. Our Class 9 Maths tuition provides real-time examples, diagrams, and visual aids to strengthen understanding. Regular practice and doubt-clearing sessions make mastering lines and angles effortless and enjoyable.

Line

A line has length but no width and no thickness.

Angle

An angle is the union of two non-collinear rays with a common initial point. The common initial point is called the 'vertex' of the angle and two rays are called the 'arms' of the angles.

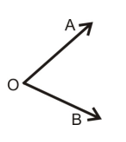
Remark:

Every angle has a measure and unit of measurement is degree.

• One right angle = 90°
• 1° = 60' (minutes)
• 1' = 60" (Seconds)

Angle addition axiom: If X is a point in the interior of ∠BAC, then μ∠BAC = μ∠BAX + μ∠XAC

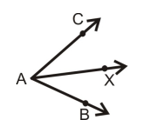
Types of Angles

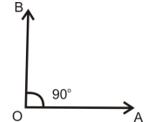
Right angles

An angle whose measure is 90° is called a right angle.

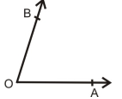
Acute angle

An angle whose measure is less than 90° is called an acute angle. 0° < ∠BOA < 90°

Obtuse angle

An angle whose measure is more than 90° but less than 180° is called an obtuse angle. 90° < ∠AOB < 180°

Straight angle

An angle whose measure is 180° is called a straight angle.

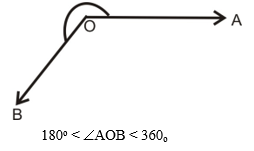
Reflex angle

An angle whose measure is more than 180° is called a reflex angle. 180° < ∠AOB < 360°

Complementary angles

Two angles, the sum of whose measures is 90° are called complementary angles. ∠AOC & ∠BOC are complementary as ∠AOC + ∠BOC = 90°

Supplementary angles

Two angles, the sum of whose measures is 180°, are called the supplementary angles. ∠AOC & ∠BOC are supplementary as their sum is 180°.

Angle Bisectors

A ray OX is said to be the bisector of ∠AOB, if X is a point in the interior of ∠AOB, and ∠AOX = ∠BOX.

DD

Adjacent angles

Two angles are called adjacent angles, if:

• they have the same vertex,
• they have a common arm,
• non common arms are on either side of the common arm.

∠AOX and ∠BOX are adjacent angles, OX is common arm, OA and OB are non common arms and lies on either side of OX.

Linear pair of angles

Two adjacent angles are said to form a linear pair of angles, if their non common arms are two opposite rays.

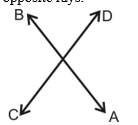
Vertically opposite angles

Two angles are called a pair of vertically opposite angles, if their arms form two pairs of opposite rays.

∠AOC & ∠BOD form a pair of vertically opposite angles. Also ∠AOD & ∠BOC form a pair of vertically opposite angles.

Angles made by a Transversial with two Parallel lines

Transversal

A line which intersects two or more given parallel lines at distinct points is called a transversal of the given lines.

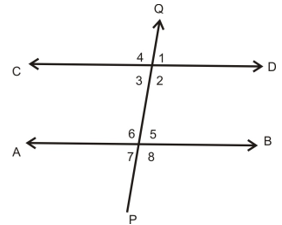
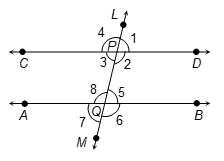
Corresponding angles

Two angles on the same side of transversal are known as the corresponding angles if both lie either above the two lines or below the two lines. In figure ∠1 & ∠5, ∠4 & ∠8, ∠2 & ∠6, ∠3 & ∠7 are the pairs of corresponding angles.

Alternate interior angles

∠3 & ∠5, ∠2 & ∠8, are the pairs of alternate interior angles.

Consecutive interior angles

The pair of interior angles on the same side of the transversal are called pairs of consecutive interior angles. In figure ∠2 & ∠5, ∠3 & ∠8, are the pair of consecutive interior angles.

Corresponding angles axiom

If a transversal intersects two parallel lines, then each pair of corresponding angles are equal. Conversely, if a transversal intersects two lines, making a pair of equal corresponding angles, then the lines are parallel.

Pairs of Angles

Axiom 1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180º.

When the sum of two adjacent angles is 180º, then they are called as linear pair of angles.

Axiom 2: If the sum of two adjacent angles is 180º, then the non-common arms of the angles form a line.

The two axioms above together is called the Linear Pair Axiom.

Theorem 1: If two lines intersect each other then the vertically opposite angles are equal.

Given: Two lines AB and CD intersect at a point O.

To prove:

• (i) ∠AOC = ∠DOB
• (ii) ∠BOC = ∠AOD

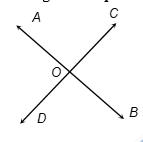
Proof: Since ray OD stands on line AB

∴ ∠AOD + ∠BOD = 180° …(i) [linear pair]

Again, ray OA stands on line CD

∴ ∠AOD + ∠AOC = 180° …(ii) [linear pair]

From equation (i) and (ii), we have

∠AOD + ∠BOD = ∠AOD + ∠AOC

⇒ ∠BOD = ∠AOC

Thus, ∠AOC = ∠DOB

Similarly we can prove that ∠BOC = ∠AOD

Example 1. If ∠BOC = 4y and ∠AOC = 6y + 30. What will be the value of y to make AOB a line?

Sol. ∠BOC + ∠AOC = 180º [Linear pair]

⇒ 4y + 6y + 30º = 180º

⇒ 10y = 180º – 30º

⇒ 10y = 150º

⇒ y = 15º

Axiom 3: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.

Axiom 4: If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.

Theorem 2: If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.

Theorem 3: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.

Theorem 4: If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.

Theorem 5: If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary then the two lines are parallel.

Theorem 6: Lines which are parallel to the same line are parallel to each other.

Example 2. In figure, 'P' is a transversal to lines 'm' and 'n'. ∠2 = 120° and ∠5 = 60°. Prove that m || n.

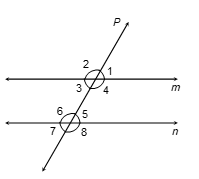
Sol. We have ∠1 + ∠2 = 180° [Linear pair axiom]

But, ∠2 = 120° [Given]

∴ ∠1 + 120° = 180°

⇒ ∠1 = 180° − 120° = 60°

Also ∠5 = 60° [Given]

∴ ∠1 = ∠5

But ∠1 and ∠5 are corresponding angles

Hence, m || n

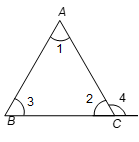
Theorem 7: Angles sum property of a triangle.

The sum of three angles of a triangle is 180°.

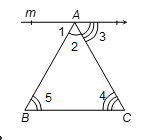
Given: A triangle ABC

To Prove: ∠2 + ∠5 + ∠4 = 180°

Construction: Through A, draw a line 'm' parallel to BC

Proof: Since m || BC and transversal AB intersects at A and B respectively, therefore we have

∠1 = ∠5 …(i) [alternate angles]

Similarly, m || BC and the transversal AC intersects them at A and C respectively.

So, ∠3 = ∠4 …(ii) [alternate angles]

Adding equation (i) and (ii), we have

∠1 + ∠3 = ∠5 + ∠4

Adding ∠2 to both sides, we have

∠1 + ∠2 + ∠3 = ∠5 + ∠4 + ∠2

But, ∠1 + ∠2 + ∠3 = 180° [Linear pair]

Hence, ∠2 + ∠5 + ∠4 = 180° [proved]

Theorem 8: Exterior angle theorem

If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.

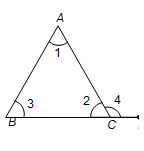
Given: A triangle ABC. D is a point on BC produced, forming exterior ∠ACE.

To prove: ∠ACD = ∠BAC + ∠ABC

Proof: In △ABC

We have ∠1 + ∠2 + ∠3 = 180° [Angle sum property] …(i)

Also ∠2 + ∠4 = 180° [linear pair] …(ii)

From (i) and (ii), we get

∠1 + ∠2 + ∠3 = ∠2 + ∠4

⇒ ∠1 + ∠3 = ∠4

Hence ∠4 = ∠1 + ∠3

or ∠ACD = ∠BAC + ∠ABC

Corollary 1: An exterior angle of a triangle is greater than either of the interior opposite angles.

Proof: Let ABC be a triangle whose side BC is produced to form exterior angle ∠4

Thus ∠1 + ∠3 = ∠4

⇒ ∠4 > ∠1 and ∠4 > ∠3

Example 3. In figure AC = BC and ∠ACP = 140º find x and y

Sol. In △ABC

∵ BC = AC [Given]

∴ ∠y = ∠ABC [Angles opposite to equal sides]

∴ 140º = y + y [Exterior angle property]

or y = 70º

∴ ∠ACB = 180º – 140º = 40º [Linear pair]

∴ x = y + ∠ACB [Exterior angle property]

∴ x = 70º + 40º = 110º

Lines and Angles - Summary

✓ If a ray stands on a line then the sum of two adjacent angles so formed is 180°.

✓ If two lines intersect each other, then the vertically opposite angles are equal.

✓ Acute angle measures between 0° and 90°.

✓ Right angle is exactly equal to 90°.

✓ Obtuse angle measures between 90° and 180°.

✓ Straight angle is exactly equal to 180°.

✓ Reflex angle measures between 180° and 360°.

✓ Complete angle is exactly equal to 360°.

✓ Two angles whose sum is 90° are called complementary angles.

✓ Two angles whose sum is 180° are called supplementary angles.

✓ Part of a line with two end points is called a line segment.

✓ Part of a line with one end point is called a ray.

✓ Three or more points lying on a line are called collinear points.

✓ An angle is formed when two rays are drawn in different directions from a common initial point.

✓ If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.

✓ If a transversal intersects two lines such that a pair of corresponding angles is equal, then the lines are parallel to each other.

✓ If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.

✓ If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.

✓ If a transversal intersects two parallel lines, then each pair of interior angles on the same side of transversal is supplementary.

✓ If a transversal intersects two lines such that a pair of interior angles on the same side of transversal is supplementary, then the two lines are parallel.

✓ Interior angles on the same side of transversal are called co-interior angles.

✓ Lines which are parallel to the same line are parallel to each other.

✓ If a side of a triangle is produced, then the exterior angle so formed is equal to sum of two interior opposite angles.

✓ The sum of angles of a triangle is 180°.

Questions:

Ques. In the figure, AB and CD are two intersecting lines. OP and OQ are respectively bisectors of ∠BOD and ∠AOC. Prove that OP and OQ are opposite rays.

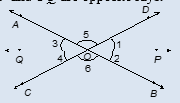
Ques. In the figure, three lines p, q and r are concurrent at O. If a = 50° and b = 90°, find c, d, e and f.

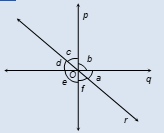
Ques. In the figure lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all angles.

Ques. Two supplementary angles are in ratio 4 : 5, find the angles.

Ques. If an angle differs from its complement by 10°, find the angle.

Answers:

2. c = 40°, d = 50°, e = 90°, f = 40°
3. ∠POR = 75°, ∠ROQ = 105°, ∠POS = 105°, ∠SOQ = 75°
4. 80° & 100°
5. 50°

Detailed Solutions

Q1. In the figure, AB and CD are two intersecting lines. OP and OQ are respectively bisectors of ∠BOD and ∠AOC. Prove that OP and OQ are opposite rays.

Sol. ∵ OP is the bisector of ∠BOD

∴ ∠1 = ∠2 …(i)

∵ OQ is the bisector of ∠AOC

∴ ∠3 = ∠4 …(ii)

∵ Lines AB and CD intersect at O

∴ ∠5 = ∠6 [vertically opp. ∠s] …(iii)

By adding (i), (ii) and (iii), we have

∠1 + ∠5 + ∠3 = ∠2 + ∠6 + ∠4 …(iv)

Now, ∠1 + ∠5 + ∠3 + ∠2 + ∠6 + ∠4 = 360° [∵ Sum of ∠s at a point = 360°]

⇒ (∠1 + ∠5 + ∠3) + (∠1 + ∠5 + ∠3) = 360° [Using (iv)]

⇒ 2(∠1 + ∠5 + ∠3) = 180°

⇒ ∠1 + ∠5 + ∠3 = 180°

⇒ ∠POQ = 180°

Hence, OP and OQ are opposite rays.

Q2. In the figure, three lines p, q and r are concurrent at O. If a = 50° and b = 90°, find c, d, e and f.

Sol. Using linear pair axiom, we have

a + b + c = 180°

⇒ 50° + 90° + c = 180° [a = 50°, b = 90°]

⇒ c = 40°

We have:

• a = d = 50° [Vertically opposite angles]
• b = e = 90° [Vertically opposite angles]
• c = f = 40° [Vertically opposite angles]

Hence, the angles c, d, e and f are of 40°, 50°, 90° and 40° respectively.

Q3. In the figure lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all angles.

Sol. ∠POR + ∠ROQ = 180° (linear pair of angles)

∠POR : ∠ROQ = 5 : 7 (given)

∴ ∠POR = (5/12) × 180° = 75°

Similarly, ∠ROQ = (7/12) × 180° = 105°

Now, ∠POS = ∠ROQ = 105° [vertically opposite ∠s]

and, ∠SOQ = ∠POR = 75° [vertically opposites]

Q4. Two supplementary angles are in ratio 4 : 5, find the angles.

Sol. Let angles are 4x & 5x.

∵ Angles are supplementary

∴ 4x + 5x = 180° ⇒ 9x = 180°

⇒ x = 180°/9 = 20°

∴ Angles are 4 × 20°, 5 × 20° ⇒ 80° & 100°

Q5. If an angle differs from its complement by 10°, find the angle.

Sol. Let angle is x° then its complement is 90° – x°.

Now given x° – (90° – x°) = 10°

⇒ x° - 90° + x° = 10°

⇒ 2x° = 10° + 90° = 100°

⇒ x° = 100°/2 = 50°

∴ Required angle is 50°.

Illustrations

Q1. In the figure, 'm' and 'n' are two plane mirrors parallel to each other. Prove that incident ray CA is parallel to reflected ray BD.

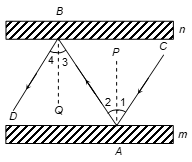
Sol.

Given: m || n and the incident ray CA at A on the first mirror 'm' is reflected in the direction BD from the second mirror 'n'.

To Prove: CA || BD

Construction: Draw perpendiculars (normal) AP and BQ at A and B respectively of the two plane mirrors.

Proof: CA is the incident ray and AB is the reflected ray.

As Angle of incidence = Angle of reflection

∴ ∠1 = ∠2 ... (i)

Again, AB is the incident ray and BD is the reflected ray.

∴ ∠3 = ∠4 ... (ii)

∵ AP ⊥ m and BQ ⊥ n [By construction]

and m || n [Given]

∴ AP || BQ [⊥ on the parallel basis are parallel to each other]

∴ AP || BQ and AB intersects them

∴ ∠2 = ∠3 [alternate angles] ... (iii)

From (i), (ii) and (iii), we get

∠1 = ∠4 ... (iv)

Adding (iii) and (iv), we get ∠1 + ∠2 = ∠3 + ∠4

⇒ ∠CAB = ∠ABD

But these are alternate angles.

Hence, CA || BD

Q2. Prove that bisector GM and HL of alternate angles AGH and DHG respectively are parallel to each other if AB || CD.

Sol. Since lines AB || CD and the transversal EF intersects them at G and H respectively

∴ ∠AGH = ∠DHG (alternate interior angles).

⇒ (1/2)∠AGH = (1/2)∠DHG

Also GM and LH are bisectors of angles ∠AGH and ∠DHG

Therefore, ∠MGH = ∠LHG

But, ∠MGH and ∠LHG are a pair of alternate angles formed when the transversal GH intersects the two lines GM and HL at G and H respectively.

Hence GM || HL.

Q3. In the figure, AB || CD. Find the value of x.

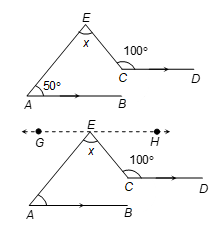
Sol.

Construction: Through E draw a line GEH || AB || CD

Proof: GE || AB and EA is a transversal.

∴ ∠GEA = ∠EAB = 50° [alternate interior ∠s]

Again, EH || CD and EC is a transversal.

∴ ∠HEC + ∠ECD = 180° [Consecutive interior ∠s]

⇒ ∠HEC + 100° = 180° ⇒ ∠HEC = 80°

Now, GEH is a straight line.

∴ ∠GEA + ∠AEC + ∠HEC = 180° [straight angle]

⇒ 50° + x + 80° = 180° ⇒ x = 50°.

Hence, x = 50°.

Q4. In the given figure, AB || CD. Find the value of x.

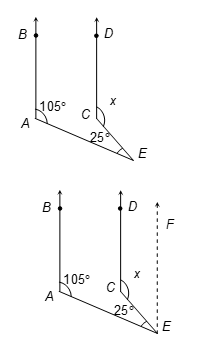
Sol.

Construction: From E, draw EF || AB || CD.

Proof: EF || CD and CE is the transversal.

∴ ∠DCE + ∠CEF = 180° [Consecutive Int. ∠s]

⇒ x + ∠CEF = 180°

⇒ ∠CEF = (180° − x) …(i)

Again, EF || AB and AE is the transversal.

∴ ∠BAE + ∠AEF = 180° [Consecutive interior ∠s]

⇒ 105° + ∠AEC + ∠CEF = 180°

⇒ 105° + 25° + (180° − x) = 180° ⇒ x = 130°. [from (i)]

Hence, x = 130°

Exercise 1 - Multiple Choice Questions

Ques. If two lines intersected by a transversal, then each pair of corresponding angles so formed is:

(a) Equal

(b) Complementary

(c) Supplementary

(d) None of these

Ques. Two parallel lines have:

(a) a common point

(b) two common point

(c) no any common point

(d) infinite common points

Ques. An angle is 14° more than its complementary angle then angle is:

(a) 38°

(b) 52°

(c) 50°

(d) none of these

Ques. The angle between the bisectors of two adjacent supplementary angles is:

(a) acute angle

(b) right angle

(c) obtuse angle

(d) none of these

Ques. If one angle of triangle is equal to the sum of the other two then triangle is:

(a) acute a triangle

(b) obtuse triangle

(c) right triangle

(d) none

Ques. X lines in the interior of ∠BAC. If ∠BAC = 70° and ∠BAX = 42° then ∠XAC =

(a) 28°

(b) 29°

(c) 27°

(d) 30°

Ques. If the supplement of an angle is three times its complement, then angle is:

(a) 40°

(b) 35°

(c) 50°

(d) 45°

Ques. Two angles whose measures are a & b are such that 2a - 3b = 60° then 4a/5b = ? If they form a linear pair:

(a) 0

(b) 8/5

(c) 1/2

(d) 2/3

Ques. Which one of the following statements is not false:

(a) if two angles forming a linear pair, then each of these angles is of measure 90°

(b) angles forming a linear pair can both be acute angles

(c) one of the angles forming a linear pair can be obtuse angle

(d) bisectors of the adjacent angles form a right angle

Ques. Which one of the following is correct:

(a) If two parallel lines are intersected by a transversal, then alternate angles are equal

(b) If two parallel lines are intersected by a transversal then sum of the interior angles on the same side of transversal is 180°

(c) If two parallel lines intersected by a transversal then corresponding angles are equal

(d) All of these

Answers to Exercise 1

1.	(d)	2.	(c)	3.	(b)	4.	(b)	5.	(c)
6.	(a)	7.	(d)	8.	(b)	9.	(c)	10.	(d)

Exercise 2

Ques. The supplement of an angle is one third of itself. Determine the angle and its supplement.

Ques. Two complementary angles are such that two times the measure of one is equal to three times measure of the other. Find the measure of the large angle.

Ques. Find the complement of each of the following angles.

(a) 36°40' (b) 42°25'36"

Ques. Write the supplementary angles of the following angles.

(a) 54°28' (b) 98°35'20"

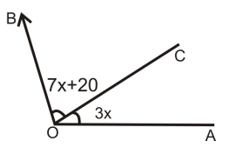
Ques. In figure, if ∠BOC = 7x + 20° and ∠COA = 3x, then find the value of x for which AOB becomes a straight line.

Ques. In figure, if x + y = w + z then prove that AOB is a straight line.

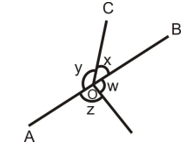
Ques. If the bisectors of two adjacent angles form a right angle prove that their non common angles are in the same straight line.

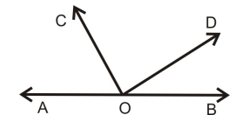
Ques. In figure, find ∠COD when ∠AOC + ∠BOD = 100°.

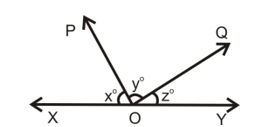
Ques. In figure x : y : z = 5 : 4 : 6. if XOY is a straight line find the values of x, y and z.

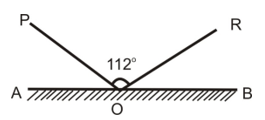
Ques. In the given figure, AB is a mirror, PO is the incident ray and OR, the reflected ray. If ∠POR = 112° find ∠POA.

Ques. In figure, if AB║ CD ║EF and y : x = 3 : 7 find x

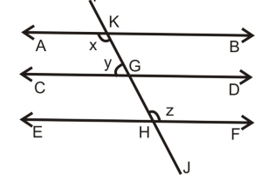
Ques. In figure if AB║CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.

Ques. △ABC is an isosceles triangle in which ∠B = ∠C and L & M are points on AB & AC respectively such that LM║BC. If ∠A = 50° find ∠LMC.

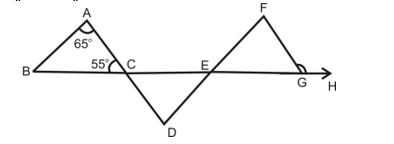
Ques. In figure if AB║ DF, AD║FG, ∠BAC = 65°, ∠ACB = 55°. Find ∠FGH

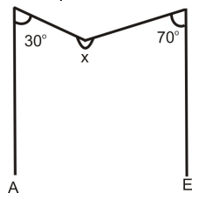
Ques. In figure, AB║ED and ∠ABC = 30°, ∠EDC = 70° then find x°.

Answers to Exercise 2

• 135^o, 45^o
• 54^o
• (a) 53^o20’ (b) 47^o34’ 24”
• (a) 125^o32’ (b) 81^o24’ 40”
• 16^o
• 80^o
• 60^o,48^o,72^o
• 34
• 126^o
• 126^o,36^o,54^o
• 115^o
• 125^o
• 260^o