Coordinate Geometry

About Coordinate Geometry – Class 9 Maths

Class 9 maths notes Coordinate Geometry introduces the exciting concept of locating points in a plane using ordered pairs. Our Class 9 maths notes make it easy to grasp the Cartesian system, plotting points, and understanding coordinates. The NCERT solutions for class 9 Maths explain every exercise clearly, ensuring students can easily calculate distances, midpoints, and section formulas.

Our Class 9 Maths tuition provides hands-on practice through graph-based learning. Tutors help students interpret diagrams, solve coordinate problems, and prepare for exams efficiently. With detailed explanations and visual aids, learning Coordinate Geometry becomes simple and interesting.

Co-ordinate System

In two dimensional coordinate geometry, we use generally two types of co-ordinate system.

1. Cartesian or Rectangular co-ordinate system.
2. Polar co-ordinate system.

In cartesian co-ordinate system we represent any point by ordered pair (x,y) where x and y are called X and Y co-ordinate of that point respectively.

In polar co-ordinate system we represent any point by ordered pair (r, θ) where 'r' is called radius vector and 'θ' is called vectorial angle of that point.

Ordered Pair

A pair of real numbers p and q listed in a specific order with 'p' at the first place and 'q' at the second place is called an ordered pair and written as (p, q). This ordered pair is also known as coordinates of a point in space.

(p, q) and (q, p) represent two different points.

Coordinate Axes

Draw two straight lines XOX' and YOY' intersecting at right angles at the point O. These lines are called coordinate axes or axes of reference.

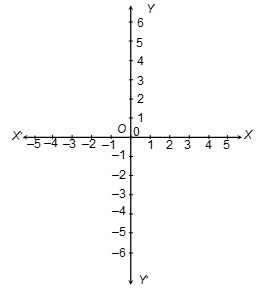
• The horizontal line XOX' is called x-axis.
• The vertical line YOY' is called y-axis.
• The point O is called the origin.
• OX represents positive x-axis.
• OX' represents negative x-axis.
• OY represents positive y-axis.
• OY' represents negative y-axis.

Any convenient unit of length is selected and mark equal distances on both axes taking the origin as zero.

Quadrants

The coordinate axes XOX' and YOY' divide the plane of paper into 4 regions. XOY, YOX', X'OY', Y'OX. These four regions are called the first, the second, the third and the fourth quadrant respectively.

• The distance measured along x-axis is called x-coordinate or abscissa.
• The distance measured along y-axis is called y-coordinate or ordinate.
• While representing the coordinates of a point, x-coordinate should be written first and y-coordinate should be written second. The P(x, y) represents the coordinates of a point P in a plane.

Convention of Signs

As discussed earlier that regions XOY, X'OY, X'OY' and XOY' are known as the first, second, third and fourth quadrants respectively. The ray OX is taken as positive X-axis, OX' as negative X-axis, OY as positive Y-axis and OY' as negative Y-axis. Thus we have,

Quadrant	X value	Y value	Designation
In first quadrant	X > 0,	Y > 0	(Positive quadrant)
In second quadrant	X < 0,	Y > 0
In third quadrant	X < 0,	Y < 0	(Negative quadrant)
In fourth quadrant	X > 0,	Y < 0

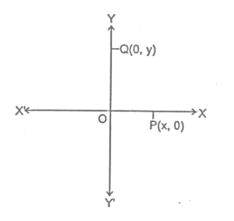
Points of Axis

In point P lies on X-axis then clearly its distance from X-axis will be zero, therefore we can say that its coordinate will be zero. In general, if any point lies on X-axis then its y-coordinate will be zero. Similarly if any point Q lies on Y-axis, then its distance from Y-axis will be zero therefore we can say its x-coordinate will be zero. In general, if any point lies on Y-axis then its x-coordinate will be zero.

Plotting of Points

In order to plot the points in a plane, we may use the following algorithm.

Step I: Draw two mutually perpendicular lines on the graph paper, one horizontal and other vertical.

Step II: Mark their intersection point as O (origin).

Step III: Choose a suitable scale on X-axis and Y-axis and mark the points on both the axis.

Step IV: Obtain the coordinates of the point which is to be plotted. Let the point be P(a,b). To plot this point start from the origin and |a| units move along OX, OX' according as 'a' is positive or negative respectively. Suppose we arrive at point M. From point M move vertically upward or downward |b| through units according as 'b' is positive or negative. The point where we arrive finally is the required point P(a,b).

Ques 1. Plot the point (3, 4) on a graph paper.

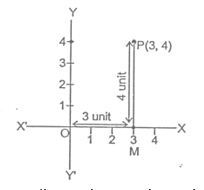
Sol. Let X'OX and Y'OY be the coordinate axis. Here given point is P(3,4), first we move 3 units along OX as 3 is positive then we arrive a point M. Now from M we move vertically upward as 4 is positive. Then we arrive at P(3,4).

Ques 2. Write the quadrants for the following points.

(i) A(3, 4)

(ii) B(-2, 3)

(iii) C(-5, -2)

(iv) D(4, -3)

(v) E(-5, -5)

Sol.

(i) Here both coordinates are positive therefore point A lies in I^st quadrant.

(ii) Here x is negative and y is positive therefore point B lies in II^nd quadrant.

(iii) Here both coordinates are negative therefore point C lines in III^rd quadrant.

(iv) Here x is positive and y is negative therefore point D lies in IV^th quadrant.

(v) Point E lies in III quadrant.

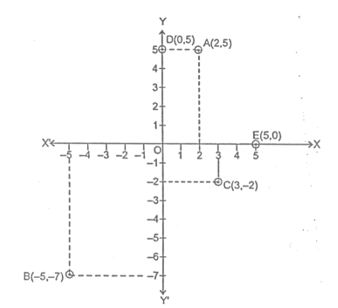
Ques 3. Plot the following points on the graph paper.

(i) A(2, 5)

(ii) B(-5, -7)

(iii) C(3, -2)

(iv) D(0, 5)

(v) E(5, 0)

Sol.

Let XOX' and YOY' be the coordinate axis. Then the given points may be plotted as given below:

Distance Between Two Points

If there are two points A (x₁, y₁) and B (x₂, y₂) on the XY plane, the distance between them is given by:

AB = d = √[(x₂ - x₁)² + (y₂ - y₁)²]

Ques 4. Find the distance between

(i) (5,3) and (3,2)

(ii) (-1,4) and (2,-3)

(iii) (a,b) and (-b,a)

Sol.

Let d₁, d₂, d₃ be the required distances. By using the formula, we have

(i) d₁ = √[(5-3)² + (3-2)²] = √[2² + 1²] = √5

(ii) d₂ = √[(-1-2)² + {4-(-3)}²] = √[(-3)² + 7²] = √58

(iii) d₃ = √[{a+(-b)}² + (b-a)²] = √[(a+b)² + (a-b)²] = √[2a² + 2b²]

Graph of Linear Equation ax + by + c₁ = 0

1. Arrange the terms to find the value of y in terms of x
   i.e. y = mx + c form
   where m = -a/b and c = -c₁/a
2. Assume three integer values of x, and get the corresponding values of y.
3. Prepare a table for the ordered pairs (x, y).
4. Plot these points on a graph paper by considering suitable scale.
5. Join these points to obtain the graph of the line ax + by + c₁ = 0.

Ex. Draw the graph of the line y = mx + c. Sol.

y = mx + c

∴ Required table is

x	0	-c/m	c/m
y	c	0	2c

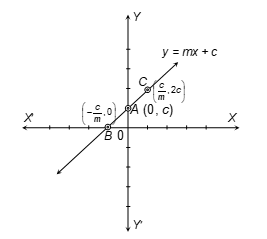
The graph of the line changes if the signs of m and c differ.

Here m (the coefficient of x) in the equation y = mx + c is known as slope of the line.

c is known as intercept on y-axis i.e., OA = c.

Questions

Ques 1. In which quadrant do the given points lie?

(i) (3, −5)

(ii) (−4, 6)

(iii) (−3, –1)

(iv) (2, 5)

Ques 2. Which of the given points lie on x or y axis: (–3, 4), (0, 8), (2, –3) (–6, 0)?

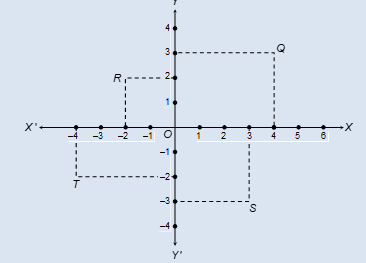
(i) The abscissa and ordinate of point Q are _____ and _____ respectively.

(ii) The y coordinate and x coordinate of point T are _____ and _____ respectively.

(iii) The coordinates of point S are (_____, _____).

(iv) (–2, 2) are coordinates of point _____.

Ques 3. Plot the points O (0, 0), A (16, 0), B (16, 12) on graph paper. Join OB, OA and BA. Name the figure and find its area.

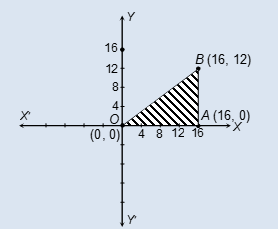
Ques 4. Plot the points O (0, 0), A (16, 0), B (16, 12) on graph paper. Join OB, OA and BA. Name the figure and find its area.

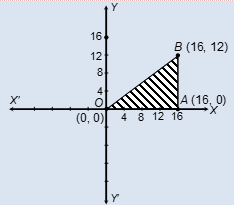
Ques 5. Draw the graph of y = 3x + 6. Use the graph to find (i) the slope (ii) intercept on y-axis (iii) the area between the line and axes.

Answers

1. (i) IV quadrant, (ii) II quadrant, (iii) III quadrant, (iv) I quadrant;

2. (0, 8) on y-axis; (–6, 0) x-axis;

3. (i) 4 and 3, (ii) – 2 and – 4, (iii) (3, – 3), (iv) R;

4. 96 square units;

5. Slope = 3, Intercept on y-axis = OA = 6 units, Area = 6 square units

Detailed Answers

Ques 1. In which quadrant do the given points lie?

(i) (3, −5)

(ii) (−4, 6)

(iii) (−3, –1)

(iv) (2, 5)

Sol.

(i) Points of the type (+, –) lie in the IV quadrant.
∴ Point (3, –5) lies in IV quadrant.

(ii) Points of the type (–, +) lie in the II quadrant.
∴ Point (–4, 6) lies in II quadrant.

(iii) Points of the type (–, –) lies in III quadrant.
∴ Point (–3, –1) lies in III quadrant.

(iv) Points of the type (+, +) lies in I quadrant.
∴ Point (2, 5) lies in I quadrant.

Ques 2. Which of the given points lie on x or y axis: (–3, 4), (0, 8), (2, –3) (–6, 0)?

Sol.

(0, 8) lies on y-axis and (–6, 0) lies on x-axis.

Ques 3. See the figure below and fill in the blanks:

(i) The abscissa and ordinate of point Q are _____ and _____ respectively.

(ii) The y coordinate and x coordinate of point T are _____ and _____ respectively.

(iii) The coordinates of point S are (_____, _____).

(iv) (–2, 2) are coordinates of point _____.

Sol.

(i) 4 and 3

(ii) – 2 and – 4

(iii) (3, – 3)

(iv) R

Ques 4. Plot the points O (0, 0), A (16, 0), B (16, 12) on graph paper. Join OB, OA and BA. Name the figure and find its area.

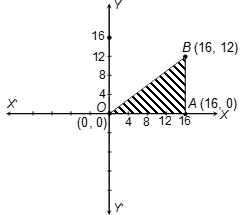
Sol.

The coordinates of O → (0, 0); A → (16, 0); B → (16, 12).

On plotting these points on the same pair of axes we get a right angle triangle OAB.

OA = 16 – 0 = 16, AB = 12 – 0 = 12

Area of right △ OAB = 1/2 × OA × AB

= 1/2 × 16 × 12

= 96 square units

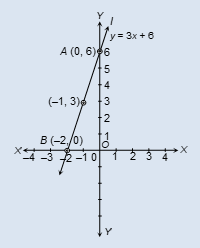
Ques 5. Draw the graph of y = 3x + 6. Use the graph to find

(i) the slope

(ii) intercept on y-axis

(iii) the area between the line and axes.

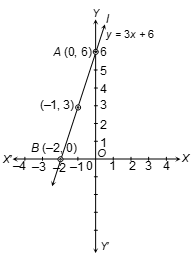
Sol.

Take y = 3x + 6 as given equation

Let x = 0 ⇒ y = 3×0 + 6 = 6

Let x = -1 ⇒ y = 3×-1+ 6 = 3

Let x = -2 ⇒ y = 3×-2 + 6 = 0

Table for y = 3x + 6

x	0	–1	–2
y	6	3	0

Plot these points on the same pair of axes and join them. The line l represents the equation y = 3x + 6.

Comparing it with y = mx + c

(i) Slope = 3

(ii) Intercept on y-axis = OA = 6 units

(iii) Area = 1/2 × OA × OB = |1/2 × 6 × −2| = 6 square units.

Illustrations

Ques 1. If the perpendicular distance of a point P from the x-axis is 3 units along the negative direction of the y-axis, write the ordinate of P.

Sol.

Ordinate = – 3

Ques 2. Write down the coordinates of the following points A, B, C and D marked on the graph as shown in figure.

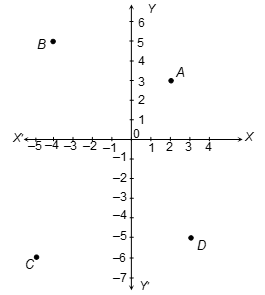
Sol.

The distance of A from y-axis is 2 units and that of from x-axis is 3 units. As A lies in the first quadrant, hence, its coordinates are (2, 3).

Point B lies in the second quadrant and its distance from y and x-axes are 4 and 5 units respectively. Hence, its coordinates are (–4, 5).

Point C lies in the third quadrant and its distances from y and x-axis are 5 and 6 units respectively. Hence, its coordinates are (–5, –6).

Point D lies in the fourth quadrant. The distance of D from y-axis is 3 unit and from x-axis is 5 units. Hence, the coordinates of D are (3, –5):

Ques 3. How will you describe the position of a flower vase in a room to another person?

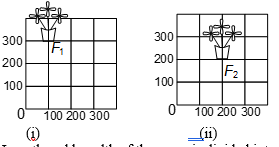
Sol.

Length and breadth of the room is divided into equal parts of 100 cm, each.

The position of flower vase in figure (i) is read as F₁ (100, 300) and in figure (ii) is read as F₂ (200, 200) with respect to the origin O.

Ques 4. Plot the points (–2, 0), (2, 0), (2, 2), (0, 4), (–2, 2) given in order. What figure do you get?

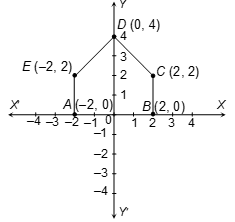
Sol.

Plot the points A (–2, 0), B (2, 0), C (2, 2), D (0, 4), E (–2, 2)

On joining these in order, we get a Pentagon ABCDE.

Ques 5. Draw the graph of the line function, the table of which is given below:

x	–4	–2	–1	0	1	2	5
y	7	p	4	q	2	r	–2

(i) Write down the linear relation between x and y.

(ii) Find the missing numbers p, q and r.

(iii) Find the slope of the above line.

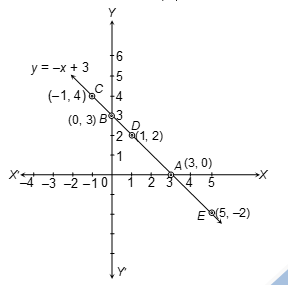
Sol.

Let linear relation between x and y is y = mx + c ...(i)

Point C(–1, 4) lies on (i), so

4 = –m + c ...(ii)

Also point D(1, 2) lies on equation (i), so

2 = m + c ...(iii)

Solving equation (ii) and (iii), we have

m = –1, c = 3

Putting the value of m and c in equation (i), we get

y = -x + 3

which is the required equation of line.

(ii) Substituting the value of x in y = –x + 3 to get corresponding value of y.

Substituting x = –2 ⇒ y = –1 × –2 + 3 = 2 + 3 = 5 ⇒ p = 5

Substituting x = 0 ⇒ y = –1 × 0 + 3 = 3 ⇒ q = 3

Substituting x = 2 ⇒ y = –1 × 2 + 3 = –2 + 3 = 1 ⇒ r = 1

∴ (p = 5, q = 3, r = 1)

(iii) Now, equation of line is y = -x + 3

Comparing with y = mx + c, we have m = -1

So, slope is –1.

Ques 6. Determine the slope and y-intercept of the line 2x + 3y + 7 = 0.

Sol.

The given line is 2x + 3y + 7 = 0

⇒ 3y = -2x - 7

⇒ y = -2/3 x - 7/3

Comparing with y = mx + c, we get

Slope = m = -2/3, y-intercept = c = -7/3.

Ques 7. Draw the graph of line y = x + c when

(i) c = – 1,

(ii) c = 0,

(iii) c = 1,

(iv) c = 2,

(v) c = 3 on the same graph.

What conclusion can you draw?

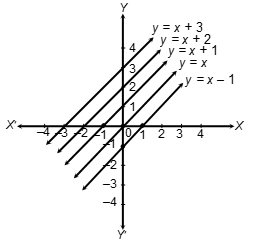
Sol.

Consider the equation y = x −1; y = x; y = x +1; y = x + 2; y = x + 3

For y = x −1

x	0	1
y	–1	0

For y = x

x	0	1
y	0	1

For y = x +1

x	0	1
y	1	2

For y = x + 2

x	0	1
y	2	3

For y = x + 3

x	0	–1
y	3	2

Ques 8. How does the graph of y = mx, depends on the value of m.

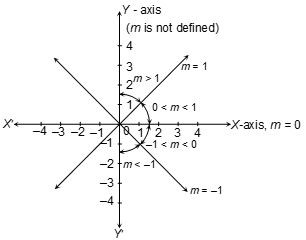
Sol.

For the graph of y = mx, the expected region, in which the graph lies, depending the value of m as:

• X-axis, m = 0
• Y-axis (m is not defined)
• m = 1
• m > 1
• 0 < m < 1
• -1 < m < 0
• m < -1
• m = -1

Ques 9. Draw the graph of the line y = mx when (i) m = 1, (ii) m = 2, (iii) m = 3, (iv) m = – 1, (v) m = – 2, (vi) m = – 3.

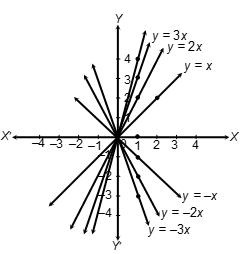
Sol.

Consider the equation of the line y = x

x	0	1
y	0	1

For y = 2x

x	0	1
y	0	2

For y = 3x

x	0	1
y	0	3

For y = 4x

x	0	1
y	0	4

For y = −x

x	0	1
y	0	–1

For y = −2x

x	0	1
y	0	–2

For y = −3x

x	0	1
y	0	–3

Ques 10. How does sign of m and c affect the positioning of the graph y = mx + c.

Sol.

For graph of y = mx + c the expected graph lines are as follow:

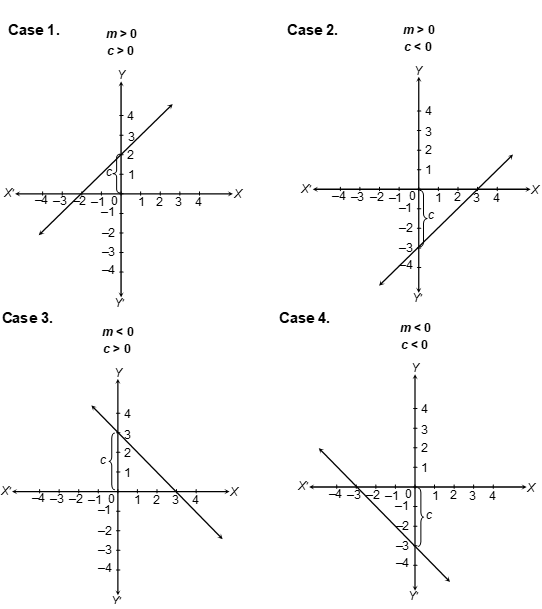
Exercise 1

Ques 1. Which point lies on x-axis

(a) (3, 2)

(b) (−3, 2)

(c) (2, 0)

(d) (−1, −2)

Ques 2. Which point lies on y-axis

(a) (1, 3)

(b) (0, 3)

(c) (5, 2)

(d) (−2, −3)

Ques 3. Which point lies above x-axis

(a) (−1, 2)

(b) (2, 0)

(c) (−1, −5)

(d) (0, −3)

Ques 4. Which point lies to the left of y-axis

(a) (2, 0) (b)

(−3, −4)

(c) (4, −2)

(d) (2, 7)

Ques 5. Which point lies to the right of y-axis

(a) (0, 3)

(b) (−2, −1)

(c) (2, 5)

(d) (−3, 2)

Ques 6. Which of the line is parallel to y = x − 2

(a) y = 2x + 1

(b) 2y = 2x − 6

(c) 2y = x + 7

(d) y = 3x + 1

Ques 7. Which point lies in IV quadrant

(a) (−2, −3)

(b) (1, −4)

(c) (−2, 3)

(d) (0, 1)

Ques 8. Which point lies in III quadrant

(a) (0, 3)

(b) (2, 0)

(c) (7, 2)

(d) (−2, −3)

Ques 9. Which graph is parallel to x-axis

(a) y = x + 1

(b) y = 2

(c) x = 3

(d) x = 2y

Ques 10. Which graph is equally inclined to both the axes

(a) x = 1/2 y

(b) x = 2 y

(c) 2y = x

(d) 2y = 2x

Ques 11. The abscissa of a point is distance of the point from:

(a) X-axis

(b) Y-axis

(c) Origin

(d) None of these

Ques 12. The y co-ordinate of a point is distance of that point from:

(a) X-axis

(b) Y-axis

(c) Origin

(d) None of these

Ques 13. If both co-ordinates of any point are negative then that point will lie in:

(a) First quadrant

(b) Second quadrant

(c) Thirst quadrant

(d) Fourth quadrant

Ques 14. If the abscissa of any point is zero then that point will lie:

(a) on X-axis

(b) on Y-axis

(c) at origin

(d) None of these

Ques 15. The co-ordinates of one end point of a diameter of a circle are (4, -1) and coordinates of the centre of the circle are (1, -3) then coordinates of the other end of the diameter are:

(a) (2,5)

(b) (-2,-5)

(c) (3,2)

(d) (-3,-2)

Ques 16. The point (-2,-1), (1,0), (4,3) and (1,2) are the vertices of a:

(a) Rectangle

(b) Parallelogram

(c) Square

(d) Rhombus

Ques 17. The distance of the point (3, 5) from X- axis is:

(a) √34

(b) 3

(c) 5

(d) None of these

Page 3.21

Answers to Exercise 1

1.	(c)	2.	(b)	3.	(a)	4.	(b)	5.	(c)
6.	(b)	7.	(b)	8.	(d)	9.	(b)	10.	(d)
11.	(b)	12.	(a)	13.	(c)	14.	(b)	15.	(b)
16.	(b)	17.	(c)

Exercise 2

Ques 1. Plot the points in the plane if its co-ordinates are given as A (5,0), B(0,3) C(7,2), D(-4,3), E(-3,-2) and F(3,-2).

Ques 2. In which quadrant do the following points lie A(2,3), B(-2,3), C(-3,-5), D(3, -1). Explain with reasons.

Ques 3. Plot the following pairs of numbers as points in the Cartesian plane.

x	–3	–2	8	4	0
y	5	0	3	8	-2

Ques 4. With rectangular axes, plot the points O(0,0), A(4,0) and C(0,6). Find the coordinates of the fourth points B such the OABC forms a rectangle.

Ques 5. Plot the points P(-3,1) and Q(2,1) in rectangular coordinate system and find all possible coordinates of other two vertices of a square having P and Q as two adjacent vertices".

Ques 6. Find the value of x, if the distance between the points (x, -1) and (3,2) is 5.

Ques 7. The base AB two equilateral triangles ABC and ABC' with side 2a, lies along the x-axis such that the mid-point of AB is at origin. Find the coordinates of the vertices C and C' of the triangles.

Ques 8. Name the quadrants in which following points lie

(a) (−2, −3)

(b) (3, – 2)

Ques 9. Determine slope and y-intercept of the graph x − √3y = 2√3.

Ques 10. Draw the graph of the equation y = 2x + 3

Ques 11. Draw the graph of y = 4x. From the graph find the value of y when x = −2

Ques 12. Draw the graph of the equation 3x + 6y = 12. Find the coordinates of the point where the graph cuts the y – axis.

Ques 13. Draw the graph of x + 10 = 0. What type of graph is it?

Ques 14. The points (−2, 5) and (3, −5) are plotted in xy plane. Find the slope and y intercept of the line joining the points.

Ques 15. Draw the graph of (i) y = −x, (ii) y = −x + 1, (iii) y = −x + 2 on the same axes.

Ques 16. Draw the graph of (i) y = 2x, (ii) y = 2x + 1, (iii) y = 2x + 3 on the same axes.

Ques 17. Draw the graph of (i) y = 2x, (ii) y = 3x, (iii) y = 4x on the same axes.

Answers to Exercise 2

Question	Answer
2.	A- Ist quadrant, B - IInd quadrant, C IIIrd quadrant, D - IVth quadrant
4.	(4, 6)
5.	(–3, 6), (2, 6) & (–3, –4), (2, –4)
6.	7 or -1
7.	C(0, √3 a), C'(0, − √3 a)
11.	(a) III Quadrant (b) IV Quadrant
12.	Slope = 1/√3, y – intercept = – 2
13.	y = −8
14.	(0, 2)
17.	slope = – 2, y – intercept = 1