The Fundamental Nature of Momentum and Its Physical Significance
Momentum represents one of the most fundamental quantities in physics, embodying the very essence of motion itself. When we define momentum as the product of mass and velocity (P = mv), we're capturing something profound about how objects interact with the world around them. A massive truck moving slowly can have the same momentum as a small car moving rapidly, demonstrating that momentum depends equally on how much matter is moving and how fast it's moving. This concept becomes particularly important when we consider that momentum is a vector quantity, meaning it has both magnitude and direction. The vectorial nature of momentum is crucial in understanding collision dynamics, where the direction of motion after impact depends not just on the speeds involved, but on the precise directional components of the momenta before collision. In the SI system, momentum is measured in kg-m/s, which elegantly combines the fundamental units of mass and velocity, while its dimensional analysis as MLT⁻¹ reveals its deep connection to the basic quantities of mechanics.
Centre of Mass: The Mathematical Heart of Systematic Motion
The concept of centre of mass provides a powerful mathematical tool for simplifying complex multi-body systems into manageable calculations. When we define the centre of mass as the point where the entire mass of a system can be considered concentrated, we're essentially creating a representative point that captures the average position of all the mass in the system, weighted by the actual mass distribution. For a system of discrete particles, the centre of mass coordinates are calculated using xcm = (Σmixi)/Σmi, which represents a mass-weighted average of all particle positions. This mathematical formulation becomes particularly elegant when extended to continuous mass distributions, where we replace discrete sums with integrals over infinitesimal mass elements. The physical significance of the centre of mass becomes apparent when we realize that external forces act on the system as if all the mass were concentrated at this single point. This principle dramatically simplifies the analysis of complex systems, allowing us to treat a spinning, tumbling object as a single particle located at its centre of mass when analyzing its translational motion.
The Profound Implications of Momentum Conservation
The principle of conservation of momentum stands as one of the most fundamental laws in physics, stemming directly from Newton's third law and the symmetry properties of space and time. When no external forces act on a system, the total momentum remains constant, which mathematically translates to Σpi(initial) = Σpi(final). This conservation principle has far-reaching implications that extend beyond simple collision problems. In rocket propulsion, for instance, the conservation of momentum explains how spacecraft can accelerate in the vacuum of space by expelling mass in the opposite direction to their desired motion. The rocket equation, vf - vi = -vrel ln(Mf/M0), emerges directly from momentum conservation and reveals the logarithmic relationship between mass ratio and velocity change. This same principle governs phenomena ranging from the recoil of firearms to the motion of astronomical bodies. When we observe the conservation of momentum in action, we're witnessing a fundamental symmetry of nature – the idea that the laws of physics remain unchanged regardless of our location in space, a principle known as translational symmetry.
Impulse and the Time-Dependent Nature of Force
The concept of impulse bridges the gap between force and momentum, revealing how forces acting over time intervals produce changes in motion. Defined as J = F·Δt = Δp, impulse represents the cumulative effect of a force acting over a specific time period. This relationship, known as the impulse-momentum theorem, provides crucial insights into collision dynamics and explains why airbags in automobiles are so effective at reducing injury. By extending the time over which a collision occurs, airbags reduce the average force experienced by passengers while maintaining the same total impulse. The mathematical formulation of impulse as the integral of force over time, J = ∫F dt, reveals that even if we don't know the exact force function during a collision, we can still determine the momentum change by calculating the area under the force-time curve. This principle finds applications in sports, where follow-through techniques increase the time of contact and thus the impulse delivered to balls or projectiles.
Collision Dynamics and Energy Considerations
Collisions represent perhaps the most dramatic demonstrations of momentum conservation, where the interplay between momentum and energy conservation creates a rich variety of physical phenomena. In elastic collisions, both momentum and kinetic energy are conserved, leading to specific mathematical relationships for the final velocities: v1 = [(m1-m2)u1 + 2m2u2]/(m1+m2) and v2 = [(m2-m1)u2 + 2m1u1]/(m1+m2). These equations reveal fascinating special cases, such as the complete velocity exchange that occurs when two objects of equal mass collide elastically. The coefficient of restitution, e = (relative velocity of separation)/(relative velocity of approach), provides a measure of how "bouncy" a collision is, ranging from e = 1 for perfectly elastic collisions to e = 0 for perfectly inelastic collisions where objects stick together. The loss of kinetic energy in inelastic collisions, given by ΔKE = ½(m1m2)/(m1+m2)²(1-e²), demonstrates how mechanical energy can be converted to other forms like heat, sound, and deformation energy while momentum remains conserved. This interplay between momentum conservation and energy transformation underlies many practical applications, from the design of crumple zones in vehicles to the analysis of particle interactions in high-energy physics experiments.
1. Momentum
Definition: Momentum is the quantity of motion contained in a body, measured by the product of mass and velocity.
Formula: P = m·v
- Units: kg-m/s (SI), gram-cm/s (CGS)
- Dimensions: MLT⁻¹
2. Centre of Mass
Definition: The point where the entire mass of a body can be considered concentrated, behaving similarly to external forces as the whole body would.
For discrete particles:
- xcm = (m₁x₁ + m₂x₂ + ... + mₙxₙ)/(m₁ + m₂ + ... + mₙ)
- Similar expressions for ycm and zcm
Key principle: In a uniform gravitational field, centre of mass and centre of gravity coincide.
3. Motion of Centre of Mass
Velocity of centre of mass: vcm = (m₁v₁ + m₂v₂ + ... + mₙvₙ)/(m₁ + m₂ + ... + mₙ)
Acceleration of centre of mass: acm = ΣFext/M
Important note: In the absence of external forces, the centre of mass either remains at rest or moves with uniform velocity.
4. Conservation of Linear Momentum
Principle: When no external force acts on a system, the total momentum remains constant.
Mathematical expression: If ΣFext = 0, then P₁ + P₂ + ... + Pₙ = constant
Applications:
- Gun-bullet recoil problems
- Collision analysis
- Rocket propulsion
5. Impulse
Definition: The product of net force and time interval over which it acts.
Formula: J = F·Δt = Δp (change in momentum)
Impulse-momentum theorem: The change in momentum equals the impulse delivered.
6. Rocket Equation
For a rocket in space with no external forces: Tsiolkovsky equation: vf - vi = -vrel ln(Mf/M₀)
Where:
- vrel = exhaust velocity relative to rocket
- M₀ = initial mass
- Mf = final mass
7. Collisions
Types of Collisions:
A. Elastic Collisions (e = 1):
- Both momentum and kinetic energy are conserved
- Velocities after collision:
- v₁ = [(m₁-m₂)u₁ + 2m₂u₂]/(m₁+m₂)
- v₂ = [(m₂-m₁)u₂ + 2m₁u₁]/(m₁+m₂)
B. Inelastic Collisions (e < 1):
- Only momentum is conserved
- Kinetic energy is not conserved
C. Perfectly Inelastic Collisions (e = 0):
- Objects stick together after collision
- v₁ = v₂ = (m₁u₁ + m₂u₂)/(m₁ + m₂)
Coefficient of Restitution:
e = (relative velocity of separation)/(relative velocity of approach) e = (v₂ - v₁)/(u₁ - u₂)
8. Special Cases in Elastic Collisions
-
Equal masses (m₁ = m₂): Velocities exchange
- Target at rest (u₂ = 0):
- Light projectile, heavy target: v₁ ≈ -u₁, v₂ ≈ 0
- Heavy projectile, light target: v₁ ≈ u₁, v₂ ≈ 2u₁
9. Two-Dimensional Collisions
For oblique collisions:
- Apply conservation of momentum in both x and y directions
- Use energy conservation for elastic collisions
- Consider coefficient of restitution along the line of impact
10. Key Formulas Summary
-
Momentum: P = mv
- Centre of mass velocity: vcm = (Σmᵢvᵢ)/Σmᵢ
- Conservation of momentum: Σpᵢnitial = Σpfinal
- Impulse: J = FΔt = Δp
- Coefficient of restitution: e = (separation velocity)/(approach velocity)
- Loss in kinetic energy: ΔKE = ½(m₁m₂)/(m₁+m₂)²(1-e²)
11. Important Applications
- Ballistic pendulum
- Rocket propulsion
- Recoil problems
- Nuclear reactions
- Sports (collision of balls)
- Traffic accident analysis
Momentum & Center of Mass
Understand the fundamental concepts, definitions, and mathematical formulations that form the foundation of momentum physics.
Conservation Laws
Master the principle of momentum conservation with detailed derivations, examples, and real-world applications.
Impulse & Collisions
Learn about impulse-momentum theorem, elastic and inelastic collisions, and coefficient of restitution with solved examples.
Advanced Applications
Explore rocket propulsion, two-dimensional collisions, and complex problem-solving techniques for competitive exams.
Momentum and Centre of Mass
Momentum
It is defined as the quantity of motion contained in a body and is measured by the product of mass and velocity.
Momentum P = m·v
The unit of momentum is kg·m/s in SI System and gram cm/s in CGS system.
Its dimension is MLT-1.
Centre of Mass
The centre of mass of an object is defined as the point where whole mass of the body may be supposed to be concentrated and the point mass behaves similarly to an external force as the whole body would have behaved.
If the system is considered to be composed of tiny masses m₁, m₂ and so on, at co-ordinates (x₁, y₁, z₁), (x₂, y₂, z₂) and so on, then the co-ordinates of the centre of mass are given by:
xcm = ∑ ximi / ∑ mi, ycm = ∑ yimi / ∑ mi, zcm = ∑ zimi / ∑ mi
Where the sums extend over all masses composing the object. In a uniform gravitational field, the centre of mass and the centre of gravity coincide.
The position vector rcm of the centre of mass can be expressed in terms of the position vector r1, r2, ... of the particles as
rcm = (m₁r1 + m₂r2 + ⋯ ) / (m₁ + m₂ + ⋯ ) = ∑ miri / ∑ mi
In statistical language the centre of mass is a mass-weighted average of the particles.
Centre of Mass of a body having continuous distribution of mass
If the bodies given are not discrete and their distances are not specific, the centre of mass can be found out by taking an infinitely small part of mass dm at a distance x and y from the origin of
the chosen co-ordinate system.
Xcm = ∫ x dm/ ∫ dm ; Ycm = ∫ y dm / ∫ dm ; Zcm = ∫ z dm/ ∫ dm
In vector form 𝔩cm = ∫ 𝔩 dm/ ∫ dm
They are as follows
- Semi-circular Disc at 4/3\pi R from the straight edge.
- Hemispherical Shell at R/2 from the plane surface.
- Solid Hemisphere at 3/8 R from the plane surface. (Where R is the radius)
- Solid cone at h/4 from the plane surface. (where h is the height of the cone)
- Solid Hollow cone h/3 from the plane surface.
Motion of the Centre of Mass of a System of Particles
Position vector of the centre of mass of a system of particle is given by
Rcm = m1r1 + m2r2 + .......... + mnrn / m1 + m2 + .................. + mn
Differentiating both sides with respect to time, we obtain
dRcm / dt = m1 dr1/dt + m2 dr2/dt + .......... + mn drn/dt / m1 + m2 + m3 + ....... + mn
∴ The velocity of the center of mass of the system is given by
vcm = m1v1 + m2v2 + .......... + mnvn / m1 + m2 + .................. + mn
Differentiating both sides with respect to time, we obtain
dvcm/dt = m1 dv1/dt + m2 dv2/dt + .......... + mn dvn/dt / m1 + m2 + .......... + mn
∴ Acceleration of the c.m. of a system of particles.
⇒ acm = F1 + F2 + .......... + Fn / M = ΣFext / M ⇒ac.m. = ΣFext / M
If ΣFext = 0, acm = 0
NOTE: Hence in absence of any external force centre of mass of a system of particles is either at rest or in uniform motion on a straight line.
Conservation of Linear Momentum of the System of Particles
Since m₁ d⃗v₁/dt + m₂ dv₂/dt + ………… + mₙ d⃗vₙ/dt = M⃗acm
⇒ d/dt (m₁v₁ + m₂v₂ + ……… + mₙvₙ) = Σ⃗Fext
⇒ d/dt (⃗p₁ + ⃗p₂ + ……… + ⃗pₙ) = Σ⃗Fext
Where ⃗p₁, ⃗p₂, ……… and ⃗pₙ are the linear momenta of the particles?
If Σ⃗ Fext = 0
⃗p₁ + ⃗p₂ + ……… + ⃗pₙ = Constant.
Hence, in absence of any external force total momentum of a system of particles remain constant.
Impulse
The impulse of the net force, denoted by ̅J, is defined to be the product of the net force and the time interval under consideration.
̅J = ∑̅F (t2 - t1) = ∑̅F Δt (Assuming constant net force)
To see what impulse is good for, let's go back to Newton's second law as stated in terms of momentum i.e.
∑̅F = d̅P / dt
If the net force ∑̅F is constant, then d̅P/dt is also constant.
In that case, d̅P/dt is equal to the total change in momentum (̅P2 – ̅P1) during the time interval (t2 – t1), divided by the interval
∑̅F = ̅P2 – ̅P1 / t2 – t1
∴ ∑̅F (t2 – t1) = ̅P2 – ̅P1
∴ ̅J = ̅P2 – ̅P1
The change in momentum of a body during a time interval equal to the impulse of the net force that acts on the body during that interval in the direction of the change in momentum.
∑F = dP
dt
∴ t2∫t1 ∑Fdt = t2∫t1dP dt = P2∫P1 dp = P2 − P1.
The integral on the left is defined to the impulse J of the net force ∑F during this interval.
J = t2∫t1 ∑Fdt
We can define an average net force Fav such that even when ∑F is not constant, the impulse J is given by
J = ∑Fav (t2 − t1).
∑Fav
is called the impulsive force, which is very great force acting for a very small interval of time.
Rocket Equation
In distant space Fext = 0 and of dvdt is in positive direction, the direction of vrel is negative. Now M dvdt = − vrel dMdt
⇒dv = − vrel dMM
If the original mass of the rocket at t = 0 was M0 and mass of the fuel burned is m, then.
∫vfvi dv = − vrel ∫M0 − mM0dMM ⇒ vf − vi = − vrel ln M0 − mM0
Mf = M0 e− vf / vrel where Mf = M0 − m
Collisions
When bodies interact strongly for a very short time, with or without coming in actual contact, collision is said to take place.
When two bodies like a car and a truck or a cricket ball and a bat, or even two subatomic particle like a proton and a neutron collide, something very different happens as compared to, say a body that’s falling freely under gravity. In both cases, there are forces that act on the bodies (or particles) but the effects are different.
For body falling freely under gravity, the weight of the body causes it to accelerate and the velocity (if it’s falling down) and the momentum increases gradually.
On the other hand, in a collision, the change in velocity isn’t gradual, it’s sudden (abrupt). Since, a finite change in velocity occurs in a very small time interval during which the bodies come in contact. The forces of action and reaction between the colliding bodies is extremely large so much so that all other forces (except some contact forces) acting on these colliding bodies during this time interval can be neglected in comparison.
Thus, in the study of collisions, we’re going to study the effect of these forces of collisions acting between these bodies (or, particles).
(a) Since the forces of collision between two bodies (or particles) are internal forces to the system consisting of two bodies, and all other forces are to be neglected, the net linear momentum of the system remains conserved during the collision. So is the net angular momentum of the system.
(b) The other law that we can use to predict the effect of collisions is what is known as Newton’s Experimental Law of collisions: when two bodies collide, the relative velocity of separation of the two bodies, perpendicular to the surface of contact, is proportional to relative velocity of approach of the two bodies (also perpendicular to the surface of contact). The constant of proportionality (represented by e) depends only on the material of the bodies and is known as the coefficient of restitution.
If two bodies move with velocity u1 and u2 to change the velocity to v1 and v2 after collision. Then the coefficient of restitution
Coefficient of Restitution – Formula
− e = v2 − v1 /u2 − u1
or e = v2 − v1 /v1 − v2 = relative velocity of separation / relative velocity of approach
Collisions: Elastic & Inelastic collisions
Collisions can, in general, be classified as elastic or inelastic collisions.
In an elastic collision, the coefficient of restitution, e = 1 and in it the momentum as well as the kinetic energy of the system of colliding bodies remains conserved.
In inelastic collisions, e < 1. In this type of collision, only momentum remains conserved. The kinetic energy doesn’t remain conserved.
For a perfectly inelastic collision, e = 0. Here the momentum remains conserved but kinetic energy doesn’t. the colliding bodies stick together.
For normal bodies, 0 < e < 1
Velocities of Colliding Bodies after Collision
Let there be two bodies with mass m1 and m2 moving with velocity u1 and u2. They collide at an instant and acquire velocity v1 and v2 after collision. Let the coefficient of restitution of the colliding bodies be e. Then, applying Newton’s experimental law and the law of conservation of momentum we can find the value of velocities v1 and v2.
Conserving momentum of the colliding bodies before and after the collision
m1u1 + m2u2 = m1v1 + m2v2… (i)
Applying Newton’s experimental law
We have v2 − v1 / u2 − u1 = −e
v2 = v1 − e (u2 − u1) … (ii)
Putting (ii) in (i) we obtain
m1u1 + m2u2 = m1v1 + m2{ v1 − e (u2 − u1) }
v1 = u1 (m1 − e m2) / m1 + m2 + u2 m2(1 + e) / m1 + m2… (iii)
From (ii)
v2 = v1 − e (u2 − u1)
v2 = u1 m1(1 + e) / m1 + m2 + u2 (m2 − m1e) / m1 + m2 (4)
When the collision is elastic; e = 1
Finally,
v1 = m1 − m2 / m1 + m2 u1 + 2m2m1 + m2u2v2 = 2m1m1 + m2u1 + m2 − m1m1 + m2u2
(i) If m1 = m2
v1 = u2andv2 = u1
When the two bodies of equal mass collide head on elastically, their velocities are mutually exchanged.
(ii) If m1 = m2 and u2 = 0, then
v1 = 0, v2 = u1
(iii) If target particle is massive;m2 »» m1andu2 = 0
v1 = −u1and v2 = 0
The light particle recoils with same speed while the heavy target remains practically at rest.
If u2 ≠ 0, then v1 ≈ −u1 + 2u2and v2 ≈ u2
v1 = u1 and v2 = 2u1 − u2
If the target is initially at rest, u2 = 0
v1 = u1 and v2 = 2u1
The motion of heavy particle is unaffected, while the light target moves apart at a speed twice that of the particle.
v1 = v2 = u1 m1/m1 + m2 + u2 m2/m1 + m2
= u1 m1 + u2 m2/m1 + m2
Elastic Collision between particles in two Dimensions
Consider a particle A projectile that approaches another particle B (target) with initial velocity u. After the collision, the final velocities are vA and vB respectively w.r.t. the initial direction of u (taken as the x-axis here).
We can write,
m1u = m1 vA cos α + m2 vB cos β
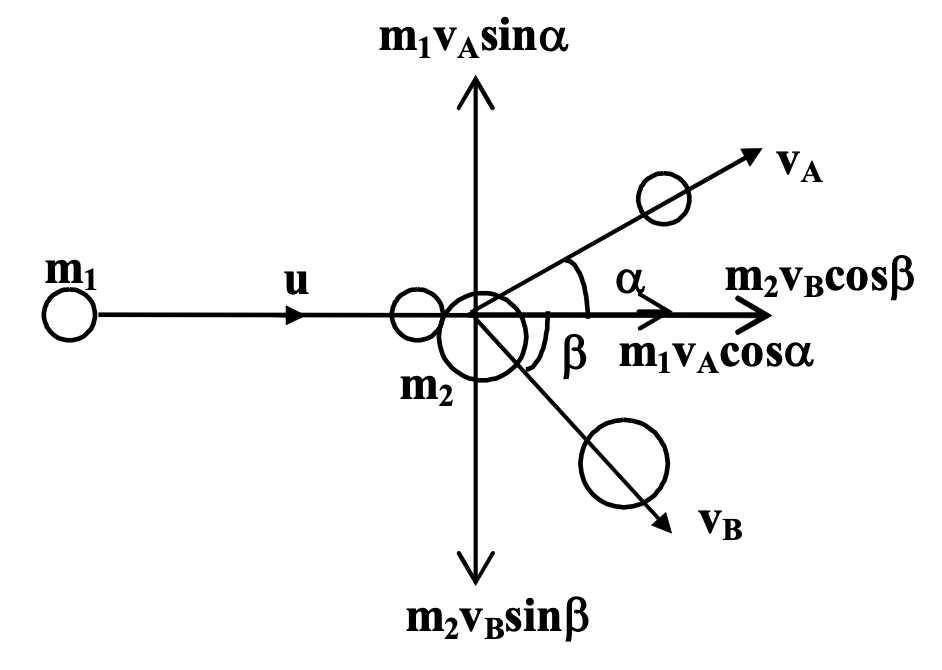
Elastic Collision Equations
0 = m1 vA sin α − m2 vB sin β . . . (1) (conservation of momentum)
since the collision is elastic, the total energy is conserved,
12 m1u12 = 12 m1vA2 + 12 m2vB2 . . . (2)
These three equations are sufficient to determine the unknowns, provided one of the angle say α is known.
Frequently Asked Questions
The fundamental necessary condition for momentum conservation is that the system must be isolated from external forces, meaning no net external force acts on the system. This isolation requirement is crucial because any external force would change the system's total momentum according to Newton's second law (F_external = dp_total/dt). When F_external = 0, the total momentum remains constant over time.
In practice, perfect isolation is impossible to achieve, but momentum conservation provides excellent approximations when external forces are negligible compared to internal interaction forces. For example, during a collision between two cars, the gravitational forces from Earth act on both vehicles, but these external forces are typically much smaller than the collision forces and act for such a brief time that their effect on the collision dynamics is negligible. Similarly, air resistance might affect the motion of colliding objects, but for short-duration, high-force interactions, this external force often has minimal impact on momentum conservation calculations.
The isolation condition also requires careful definition of system boundaries. Engineers and physicists must thoughtfully choose which objects to include in their system analysis. In analyzing a rocket launch, if the system includes only the rocket, then the expelled exhaust represents an external force, and momentum isn't conserved for the rocket alone. However, if the system includes both the rocket and the exhaust gases, then momentum is conserved for the entire system. Understanding how to properly define system boundaries while ensuring adequate isolation from external forces is essential for successfully applying momentum conservation principles in real-world problem-solving scenarios.
The apparent contradiction between momentum conservation and energy "non-conservation" in collisions stems from a misunderstanding of what conservation means for each quantity. Energy is actually always conserved in collisions—it simply transforms from kinetic energy into other forms like heat, sound, elastic potential energy, and electromagnetic radiation. Momentum, however, has no alternative forms in classical mechanics, making its conservation more straightforward and absolute.
During most real-world collisions, kinetic energy transforms into thermal energy through friction and plastic deformation, acoustic energy through sound waves, and sometimes electromagnetic energy through sparks or light emission. These energy conversions are often irreversible, meaning the thermal and acoustic energy cannot spontaneously convert back into organized kinetic motion. This irreversibility makes it appear that mechanical energy is "lost," but the total energy including all forms remains constant.
Momentum conservation is more fundamental because it emerges from the basic symmetries of space and time, while kinetic energy conservation depends on the specific interaction mechanisms between objects. In elastic collisions between hard objects like billiard balls, both momentum and kinetic energy are conserved because minimal energy converts to other forms. However, in inelastic collisions involving soft materials, significant energy transformation occurs while momentum conservation remains unaffected. This difference makes momentum conservation a more universally applicable analytical tool, since it holds regardless of material properties, collision speeds, or energy dissipation mechanisms. Understanding this distinction helps engineers and scientists choose appropriate analytical approaches for different types of collision problems and system interactions.
Inelastic collisions provide excellent examples of momentum conservation principles because they involve significant energy dissipation while maintaining perfect momentum conservation. During an inelastic collision, objects deform, heat up, and may even stick together, yet the total momentum before and after collision remains identical. This conservation occurs because the collision forces between objects are internal to the system, and internal forces cannot change the total momentum of an isolated system.
The mathematical analysis of inelastic collisions demonstrates momentum conservation clearly. For two objects with initial momenta p₁ᵢ and p₂ᵢ that undergo a perfectly inelastic collision (sticking together), the final momentum equals the vector sum: p_final = p₁ᵢ + p₂ᵢ. The final velocity of the combined object is v_final = (m₁v₁ᵢ + m₂v₂ᵢ)/(m₁ + m₂), where the masses and initial velocities determine the outcome entirely through momentum conservation.
Real-world examples include car crashes where vehicles crumple and stick together, ballistic pendulum experiments used to measure projectile velocities, and industrial processes like riveting or welding. In each case, substantial kinetic energy converts to heat, sound, and deformation energy, but momentum conservation allows engineers to predict final velocities and analyze impact forces. This principle enables crash investigators to reconstruct accidents, helps engineers design safer vehicles, and guides the development of impact-absorbing materials. The reliability of momentum conservation in inelastic collisions makes it an invaluable tool for forensic analysis, safety engineering, and industrial process design where energy dissipation is significant but predictable outcomes are required.
The conservation of momentum during kinetic energy loss highlights a fundamental distinction between these two quantities: momentum conservation is absolute in isolated systems, while kinetic energy conservation depends on the nature of interactions. Momentum is conserved because it reflects the fundamental symmetry of space, making its conservation a consequence of the basic structure of spacetime rather than the specific details of how objects interact.
Kinetic energy can be converted into other forms during collisions—heat, sound, elastic potential energy in deformed materials, or even light and electromagnetic radiation. These energy transformations don't violate conservation of energy; they simply redistribute energy among different forms. However, momentum has no alternative forms—it can only be transferred between objects or stored in field configurations, but the total momentum of an isolated system cannot change or disappear.
Consider a perfectly inelastic collision where two clay balls stick together upon impact. The final combined object moves slower than either initial object, representing a significant loss of kinetic energy converted to heat and permanent deformation. However, the vector sum of initial momenta exactly equals the final momentum of the combined system. This occurs because momentum transfer depends only on the forces between objects, and Newton's third law guarantees that internal forces cannot change total system momentum. The energy loss reflects the irreversible nature of the deformation and heating processes, while momentum conservation reflects the deeper symmetry principles that govern all physical interactions. This distinction makes momentum conservation a more reliable analytical tool for analyzing collisions and interactions where energy dissipation cannot be avoided or easily quantified.
In mass-spring systems, momentum conservation applies when considering the complete system including all interacting components, though it may not be immediately obvious due to the oscillatory nature of spring motion. When a mass is attached to a spring and set into motion, the total momentum of the mass-spring system oscillates between the mass and the spring itself. As the mass compresses the spring, momentum transfers from the mass to the spring material, and as the spring extends, momentum transfers back to the mass.
During compression, the spring experiences internal stress waves that carry momentum through the material. While we often treat springs as massless in simplified analyses, real springs have distributed mass that participates in momentum conservation. The center of mass of the entire mass-spring system moves according to momentum conservation principles, even though individual components within the system may have complex oscillatory motion. This becomes particularly important in precision engineering applications where spring mass cannot be neglected.
More subtle examples include systems with changing mass, such as rockets burning fuel or vehicles loading and unloading cargo. In these cases, momentum conservation requires careful consideration of what constitutes the system. For a rocket, if the system includes both the rocket and expelled exhaust, momentum is conserved, but if we consider only the rocket, momentum appears to change due to mass ejection. Similarly, in biological systems like bird flight or fish swimming, momentum conservation governs propulsion mechanisms where organisms push against fluid masses to generate forward motion. Understanding these non-obvious applications requires expanding our perspective to include all relevant momentum-carrying components in the system definition.
Angular momentum conservation emerges from the rotational symmetry of space, making it a fundamental principle that applies across diverse physical systems. Just as linear momentum conservation stems from spatial translation symmetry, angular momentum conservation results from the fact that physical laws remain unchanged under spatial rotation. This deep connection means that any isolated system free from external torques will conserve its total angular momentum.
In planetary systems, angular momentum conservation explains why planets maintain stable orbits and why planetary formation leads to flattened disk structures. As a rotating cloud of gas and dust collapses under gravity, conservation of angular momentum requires that the cloud spin faster as it contracts, eventually forming a disk-like structure. This same principle governs the behavior of figure skaters who spin faster when they pull their arms closer to their body, and it explains why hurricanes maintain their rotational structure as they move across ocean surfaces.
Angular momentum conservation also applies in quantum mechanical systems, where it governs electron orbital structures in atoms and determines selection rules for photon emission and absorption. In engineering applications, this principle guides the design of gyroscopes used in navigation systems, flywheels for energy storage, and reaction wheels for spacecraft attitude control. The conservation principle works because angular momentum L = r × p (where r is position vector and p is momentum) depends on both the distance from the rotation axis and the linear momentum, allowing energy-efficient control of rotational motion through mass distribution changes rather than requiring external torques.
Momentum conservation in magnetic fields presents fascinating complexities because magnetic forces can change particle trajectories without doing work on the particles. When a charged particle moves through a magnetic field, it experiences a Lorentz force F = q(v × B), where q is the particle's charge, v is its velocity, and B is the magnetic field. This force is always perpendicular to both the velocity and magnetic field, causing the particle to follow a curved path while maintaining constant speed.
For an isolated charged particle in a uniform magnetic field, the momentum magnitude remains constant, but its direction continuously changes. However, when considering the complete system including the magnetic field source, total momentum is conserved. The apparent momentum change of the charged particle is balanced by an opposite momentum change in the current-carrying conductors that generate the magnetic field. This principle underlies the operation of electric motors and generators, where momentum transfer between charged particles and current-carrying conductors produces mechanical motion.
In more complex scenarios involving multiple charged particles, momentum conservation requires careful consideration of electromagnetic field contributions. The total momentum of the system includes both mechanical momentum of particles and electromagnetic field momentum density (1/μ₀)(E × B), where E is the electric field and μ₀ is the permeability of free space. Particle accelerators exemplify this principle in practice—while individual particles gain enormous momentum as they're accelerated by electric fields and guided by magnetic fields, the total momentum of the particle-accelerator system remains conserved when accounting for the momentum stored in the electromagnetic fields and the mechanical reaction forces on the accelerator structure.
The decision to apply momentum conservation should be based on three key criteria: system isolation, problem objectives, and available information. First, assess whether the system can reasonably be considered isolated from external forces. If external forces are absent or negligible compared to internal interaction forces, momentum conservation becomes a powerful analytical tool. This often applies to collision problems, explosion analysis, and short-duration interactions where external forces like gravity or air resistance have minimal impact.
Second, consider your analytical objectives. Momentum conservation is particularly valuable when you need to relate initial and final states without detailed knowledge of the interaction process. If you're trying to determine post-collision velocities from pre-collision conditions, or vice versa, momentum conservation provides direct relationships. However, if you need to understand forces during the interaction or energy transformations, momentum conservation alone may be insufficient, requiring supplementary analysis methods.
Third, evaluate the available information and unknowns in your problem. Momentum conservation works best when you have sufficient information about masses and velocities to set up the conservation equations. For problems involving multiple unknowns, you might need to combine momentum conservation with other principles like energy conservation or kinematic relationships. In complex engineering systems, momentum conservation often serves as a starting point for analysis, providing overall constraints that guide more detailed calculations. The key is recognizing that momentum conservation offers a global perspective on system behavior, making it most valuable when you need to understand overall system changes rather than detailed local interactions.
Momentum conservation and energy conservation serve different analytical purposes, with momentum conservation often being more useful because it's more broadly applicable and easier to apply in many practical situations. Momentum is always conserved in isolated systems, regardless of whether the interactions are elastic or inelastic, while mechanical energy conservation only holds when no energy is dissipated through heat, sound, deformation, or other non-mechanical forms.
In many real-world scenarios, energy dissipation is unavoidable. Car crashes, for instance, involve significant energy conversion to heat, sound, and permanent deformation of materials. During these inelastic collisions, kinetic energy decreases substantially, making energy conservation approaches inappropriate for analyzing the collision dynamics. However, momentum conservation remains valid throughout these interactions, allowing investigators to determine pre-collision velocities and impact forces even when substantial energy is lost.
Additionally, momentum conservation calculations are often more straightforward because momentum is a vector quantity that follows simple addition rules, while energy calculations frequently require tracking multiple forms of energy transformation. In complex systems involving multiple objects and interactions, momentum conservation provides a direct relationship between initial and final states without requiring detailed knowledge of intermediate energy conversion processes. This practical advantage makes momentum conservation the preferred analytical tool for many engineering applications, forensic investigations, and physics problem-solving scenarios where energy dissipation cannot be ignored or is difficult to quantify accurately.
The conservation of momentum emerges from one of the most fundamental symmetries in nature: the homogeneity of space. This profound connection was established through Noether's theorem, which demonstrates that every continuous symmetry in physics corresponds to a conservation law. Specifically, because the laws of physics remain unchanged regardless of where you conduct an experiment in empty space, momentum must be conserved.
At its core, momentum conservation stems from Newton's third law of motion, which states that every action has an equal and opposite reaction. When two objects interact, the forces they exert on each other are equal in magnitude but opposite in direction. Since force equals the rate of change of momentum (F = dp/dt), the total change in momentum for the system is zero. This fundamental principle applies whether we're examining colliding billiard balls, exploding fireworks, or galaxies interacting across vast cosmic distances.
The mathematical foundation rests on the fact that in an isolated system one free from external forces the total momentum remains constant over time. This isn't merely an approximation or convenient assumption; it's a fundamental law that has never been observed to fail in any physical system. From subatomic particle interactions in accelerators to the motion of planets in our solar system, momentum conservation provides the bedrock for understanding how objects interact and move through space.
While momentum conservation can be derived from Newton's second and third laws, it represents a more fundamental principle that transcends the specific framework of Newtonian mechanics. This independence becomes apparent when examining quantum mechanics and relativistic physics, where Newton's laws require modification, but momentum conservation remains valid in its properly generalized forms.
In quantum mechanics, the classical concept of a definite trajectory breaks down, replaced by probability distributions and wave functions. However, momentum conservation continues to hold, though it must be understood in terms of expectation values and quantum operators rather than classical deterministic motion. Similarly, in special relativity, Newton's second law F = ma becomes invalid at high speeds, replaced by F = dp/dt where p = γmv (with γ being the Lorentz factor). Yet momentum conservation remains intact, demonstrating its independence from the specific formulation of Newton's laws.
The deeper independence stems from Noether's theorem, which shows that momentum conservation emerges from the symmetry of space translation rather than from specific force laws. This means that any physical theory respecting spatial homogeneity must incorporate momentum conservation, regardless of how forces are described. Even in general relativity, where spacetime itself becomes dynamic, momentum conservation generalizes to the conservation of the stress-energy tensor. This fundamental independence explains why momentum conservation serves as a guiding principle in developing new physical theories—it's not just a consequence of particular force laws but a requirement imposed by the basic symmetries of space and time.
The principle of conservation of linear momentum specifically addresses momentum in straight-line motion, distinguishing it from angular momentum, which involves rotational motion. Linear momentum is a vector quantity defined as p = mv, where m is mass and v is velocity vector. The principle states that in any isolated system, the total linear momentum remains constant regardless of internal interactions between system components.
Linear momentum conservation applies to one-dimensional problems like head-on collisions, two-dimensional scenarios like billiard ball interactions, and three-dimensional cases like particle physics experiments. The vector nature of linear momentum means that conservation must hold independently in each spatial dimension. If we establish coordinate axes x, y, and z, then momentum is conserved separately along each axis: Σpₓ = constant, Σpᵧ = constant, and Σpᵧ = constant.
This principle proves invaluable in analyzing complex systems where multiple objects interact simultaneously. For example, in a multi-car accident, investigators can use linear momentum conservation to determine pre-collision velocities even when the collision involves multiple vehicles moving in different directions. The principle also guides the design of particle accelerators, where precise momentum conservation calculations enable physicists to predict particle behavior after high-energy collisions. In engineering applications, linear momentum conservation helps optimize designs for everything from shock absorbers to spacecraft attitude control systems. The principle's mathematical precision allows engineers to calculate exact outcomes without modeling the complex internal forces that occur during interactions, significantly simplifying analysis of otherwise intractable problems.
The mathematical proof of momentum conservation begins with Newton's second and third laws, demonstrating that this conservation emerges naturally from more fundamental principles. Consider two objects interacting with each other in an isolated system. Newton's second law states that F = dp/dt, where F is force, p is momentum, and t is time. For object 1, we have F₁ = dp₁/dt, and for object 2, F₂ = dp₂/dt.
Newton's third law tells us that F₁ = -F₂, meaning the forces are equal in magnitude but opposite in direction. Substituting this into our momentum equations gives us dp₁/dt = -dp₂/dt, which can be rearranged as dp₁/dt + dp₂/dt = 0. This simplifies to d(p₁ + p₂)/dt = 0, indicating that the total momentum (p₁ + p₂) has zero rate of change with time.
Since the derivative of the total momentum with respect to time equals zero, the total momentum must be constant. This mathematical relationship can be extended to any number of objects: d(Σpᵢ)/dt = 0, where the summation includes all objects in the isolated system. The proof demonstrates that momentum conservation isn't an additional assumption but rather an inevitable consequence of Newton's laws. This mathematical foundation allows physicists and engineers to solve complex problems by focusing on initial and final states rather than tracking detailed force interactions throughout the process. The mathematical elegance of this proof also reveals why momentum conservation holds at quantum mechanical scales, where it emerges from the mathematical structure of quantum field theory.
The terms "law" and "principle" are often used interchangeably when referring to momentum conservation, but the dual terminology reflects both its empirical validation and its theoretical foundation. As a "law," momentum conservation represents an observed regularity in nature that has been verified countless times through experimentation and observation. Every controlled collision, explosion, and interaction ever studied has confirmed that momentum is conserved in isolated systems, establishing it as a reliable empirical law.
As a "principle," momentum conservation represents a fundamental organizing concept that guides theoretical physics and practical problem-solving approaches. Principles in physics often reflect deeper symmetries or fundamental assumptions about the nature of reality. Momentum conservation emerges from the principle that space is homogeneous—that the laws of physics are the same everywhere. This principled foundation means that momentum conservation isn't just an observed pattern but a logical consequence of how space and time are structured.
The terminology also reflects historical development in physics understanding. Early formulations were based primarily on empirical observations of collisions and mechanical systems, leading to its characterization as a law. However, as theoretical physics developed, particularly with the work of Emmy Noether in the early 20th century, the deeper connection between symmetries and conservation laws became clear, emphasizing its role as a fundamental principle. Modern physics education often uses both terms to emphasize that momentum conservation is simultaneously a well-tested empirical law and a fundamental theoretical principle that provides insight into the basic structure of physical reality.
The applications of momentum conservation span virtually every field of science and engineering, making it one of the most practically useful physics principles. In aerospace engineering, momentum conservation enables precise spacecraft navigation and orbital mechanics calculations. Mission planners use these principles to design gravity-assisted trajectories that allow spacecraft to reach distant planets using minimal fuel. The Voyager probes, for instance, used momentum conservation during planetary flybys to gain speed and change direction, allowing them to visit multiple planets in a single mission.
In manufacturing and industrial applications, momentum conservation principles guide the design of machinery ranging from hammers and pile drivers to precision instruments. Quality control processes often rely on momentum conservation analysis for example, testing the integrity of materials by analyzing how momentum transfers during impact testing. The automotive industry extensively uses these principles in crash testing, airbag deployment timing, and vehicle stability control systems. Modern anti-lock braking systems and electronic stability programs operate by managing momentum transfer between the vehicle and the road surface.
Medical applications include analyzing biomechanical systems, from joint replacement design to understanding injury mechanisms in sports medicine. Cardiovascular specialists use momentum conservation principles to understand blood flow dynamics and design artificial heart valves. In ballistics and forensic science, momentum conservation helps investigators determine projectile trajectories, impact forces, and weapon characteristics from crime scene evidence. Even in emerging technologies like magnetic levitation trains and advanced propulsion systems, momentum conservation principles guide design decisions and performance optimization strategies.
The law of conservation of momentum states that the total momentum of an isolated system remains constant over time, regardless of the interactions occurring within that system. Momentum itself is defined as the product of an object's mass and velocity (p = mv), representing the quantity of motion an object possesses. This law means that momentum can be transferred between objects during interactions, but the total amount of momentum in the system never changes.
To understand this concept intuitively, imagine two ice skaters pushing off each other. Initially, both skaters are at rest, so the total momentum of the system is zero. When they push apart, they move in opposite directions, but because momentum is a vector quantity (having both magnitude and direction), their momenta cancel each other out, maintaining the total momentum at zero. If one skater is heavier than the other, the lighter skater will move faster after the interaction, but the mathematical product of mass and velocity will be equal and opposite for both skaters.
The practical implications of this law extend far beyond simple examples. In crash investigations, forensic experts use momentum conservation to reconstruct accident scenarios, determining vehicle speeds and impact angles from the final positions of wreckage. Manufacturing processes rely on momentum conservation principles in everything from ball bearing production to precision machining operations. The law also governs more complex scenarios like fluid dynamics, where momentum conservation helps engineers design more efficient aircraft wings, ship hulls, and pipeline systems. Understanding momentum conservation provides a powerful analytical tool for predicting system behavior without needing to track every individual force and interaction.
Momentum conservation applies universally because it reflects a fundamental symmetry of space itself, transcending the specific details of how objects interact. This universality stems from the principle that the laws of physics are invariant under spatial translation—meaning physical laws work the same way whether you're in New York, Tokyo, or the Andromeda Galaxy. This spatial homogeneity directly leads to momentum conservation through Noether's theorem, establishing it as a consequence of the basic structure of spacetime rather than a specific property of particular materials or forces.
The universal nature of momentum conservation has been verified across an extraordinary range of scales and conditions. In particle physics, momentum conservation governs interactions between quarks and leptons in particle accelerators, where energies reach levels never encountered in everyday life. At the astronomical scale, momentum conservation explains how binary star systems orbit each other and how galaxy collisions unfold over millions of years. Even in quantum mechanics, where other classical concepts break down, momentum conservation remains inviolate, though it must be understood in terms of probability distributions rather than definite trajectories.
This universality makes momentum conservation an invaluable tool for understanding complex systems where detailed force calculations would be impossible. Engineers designing spacecraft trajectories, physicists analyzing particle decay processes, and biologists studying cellular interactions all rely on momentum conservation principles. The law's universal applicability means that once you understand how momentum conservation works in simple systems, you can apply the same principles to predict outcomes in vastly more complex scenarios, from industrial machinery to astrophysical phenomena.
Conservation of momentum manifests in countless real-world scenarios, making it one of the most practically relevant physics principles. In automotive safety, this principle explains why crumple zones and airbags are so effective. During a collision, the total momentum of the vehicles must be conserved, but by extending the collision time through controlled deformation, the forces experienced by passengers are dramatically reduced, potentially saving lives.
Rocket propulsion represents perhaps the most spectacular application of momentum conservation. As rockets burn fuel and expel exhaust gases at high velocity in one direction, the rocket gains momentum in the opposite direction. This principle enables spacecraft to navigate the vacuum of space where there's nothing to "push against." The Saturn V rocket that carried astronauts to the Moon relied entirely on this fundamental principle, ejecting approximately 15 tons of exhaust per second to generate the massive thrust needed for lunar missions.
In sports, momentum conservation explains phenomena that athletes intuitively understand. When a baseball pitcher throws a fastball, both the ball and the pitcher experience momentum changes, though the pitcher's much larger mass makes the effect barely noticeable. However, in ice hockey, players routinely use momentum conservation strategically—a player can pass a puck and simultaneously propel themselves backward, or two players can collide and share their combined momentum based on their masses and initial velocities. Understanding these principles helps athletes optimize their performance and coaches develop more effective strategies.