Work
It is defined as dot product of force and displacement:
W = F ⋅ s = F.s.cosθ
Where F is force acting on a point and s is displacement of the point of application of force. θ is angle between force and displacement. In case of a particle, work is said to be done when there is a change in its kinetic energy.
If w = 0, then F = 0 or S = 0 or θ = 90°.
If force is variable, then total work done by force is:
W = ∫ F ⋅ dx
Illustration 1: A block of ice is drawn through a distance 500 cm along a smooth horizontal surface. The pull in the rope is 100 dyne and the angle between the rope and ground is 30°. Find the work done.
Solution:
Work done = component of the force parallel to the displacement × displacement
W = F cos θ × s = 100 × cos 30° × 500 = 43,300 erg.
Since displacement depends on reference frame, hence work also depends on the reference frame.
Illustration 2: A block of mass 2 kg is lying on a flat car, which is accelerating with constant acceleration of 1 m/s². Find the work done by friction on the block in 10m journey of car:
a. with respect to driver of car
b. with respect to a ground observer
Solution:
(a) With respect to driver, displacement of block is zero. Work done by friction force on block is zero.
(b) With respect to ground observer, displacement is 10m and force of friction fs = ma = 2 ×
1 = 2N
Therefore, Work done by friction = 2 × 10 = 20J
Work done by a force can be positive or negative depending on whether the displacement takes place in the direction of the force or against it.
Power
The rate at which work is done (by an agent) is known as power.
Power, P = dW/dt = F ⋅ dx/dt = F ⋅ v
This is instantaneous power. For average power:
Pav = Total work done / Time taken
Illustration 3: An engine of mass 20 tons pulls a train of 20 wagons, each of mass 20 tons with constant velocity of 72 km/hr on a level track. If the coefficient of kinetic friction is μk = 0.01, find the power developed by the engine.
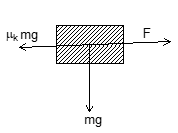
Solution:
Total forward force F = frictional force = μkmg (including engine)
Net power developed = F.v = μk(mg)v
= 0.01 x (420 x 103) x 10x 72 x 103/3600
= 0.01 x 420 x 104 x 20
Calculations yield power = 420 kW.
Energy
Energy is the capacity (of a body or agent) to do work. We focus on mechanical energy: kinetic and potential.
Kinetic Energy
K.E. = (1/2)mv²
Since velocity is reference frame dependent hence, K.E. is also reference frame dependent for example, a man sitting in a moving train holds a ball in his hand. Then kinetic energy of the ball with respect to that man is zero and with respect to observer situated on ground, it 1/2mv02. Where this m is mass of ball and v0 is speed of train.
Conservative and Non-Conservative Force
- Conservative Force: Work done in closed loop is zero (e.g., gravity, electrostatics).
- Non-Conservative Force: Work done in closed loop is not zero (e.g., friction).
Potential Energy
Potential energy is energy due to position or strain. It is reference frame dependent. Potential energy function can only be defined for conservative force field, e.g., for uniform gravity, PE = mgh.
- For gravitational force, PE = mgh
- For spring: PE = ½ kx²
Units and Dimensions
| Quantity | Work/Energy | Power |
|---|---|---|
| Dimension | ML2T-2 | ML2T-3 |
| MKS | Joule | Watt |
| FPS | ft-Poundal | ft-poundal/sec |
| CGS | erg | erg/sec |
| Practical (Other) | kWh, eV, cal | HP, KW, MW |
- 1 Joule = 1 Newton x 1 m = 105 dyne x 102 cm = 107 erg
- 1 watt = 1 Joule/ sec = 107 erg/sec.
- 1 ft. poundal = 1 poundal x 1 ft = 13825 dyne x 30.48 cm = 4.214 x 105 erg
- 1kg-m = 1kg- wt x 1 m
= "g" Newton x 1m = "g" Joule = 9.8 Joule - 1ft-lb = "g" poundal x 1 ft
32.2 poundal x 1ft
32.2 ft-poundal - 1 kwh = 103 watt x 1 hr = 103 watt x 3600 sec
= 3.6 x 106 Joule - 1HP = 550 ft. lb/sec (by definition)
= 32.2 x 550 x 4.214 x 105 erg/sec. = 746 x 107 erg/sec.
= 746 watt. - 1 MW = 106 watt.
- 1 cal = 1 calorie = 4.2 Joule
- 1eV = "e" Joule = 1.6 x 10-19 Joule
- (e = magnitude of charge on the electron in colombs)
Formulae and Concepts at a Glance
- Work: W = F.s = Fscosθ
- Work (vector): Fxx + Fyy + Fzz
- Gravitational PE = mgh
- Kinetic Energy = (1/2)mv²
- Spring: F = Kx, PE = (1/2)Kx²
- Power = work/time = energy/time
Solved Problems
Problem 1: A block of mass 10 kg accelerates uniformly from rest to a speed of 2m/s in 20 seconds. The average power in time interval 0 to 20 seconds is:
(A) 10W
(B) 1W
(C) 20W
(D) 2W
Solution: Average power = Net work done / Time taken
Net work done = Final KE = ½ × 10 × 2² = 20J; Pav = 20/20 = 1W
Answer: (B)
Problem 2: An electric motor creates a tension of 4500N in a hoisting cable and reels it at the rate of 2 m/s. What is the power of electric motor?
(A) 15KW
(B) 9KW
(C) 225W
(D) 9000HP
Solution: Power developed = F.v = 4500 × 2 = 9000W = 9KW
Answer: (B)
Problem 3: A pumping machine pumps a liquid at a rate of 60 cc per minute at a pressure of 1.5 atmosphere. The power of the machine is:
(A) 9 watts
(B) 6 watts
(C) 9 KW
(D) None of these
Solution: Power = Pressure × (dV/dt). Calculation yields Power = 9W.
Answer: (A)
Problem 4: A block of mass m moving with a velocity v0 on a smooth horizontal floor collides with a light spring of stiffness k that is fixed (horizontally with a vertical wall). If the maximum force imparted by the spring on the block is F, then:
(A) F ∝ m
(B) F ∝ k
(C) F ∝ v0
(D) All the above
Solution: By energy conservation: Fmax ∝ √k, ∝ √m, ∝ v₀.
Answer: (D)
Problem 5: A particle moves with a velocity (5i – 3j + 6k) m/s under influence of a force (10i + 10j + 20k)N. Find the instantaneous power.
(A) 200 J/s
(B) 40 J/s
(C) 140 J/s
(D) 170 J/s
Solution: Power = F ⋅ v = (5 × 10) + (–3 × 10) + (6 × 20) = 50 – 30 + 120 = 140 J/s
Answer: (C)
Assignment Problems
Ques. A body of mass 4kg and momentum 2Ns has kinetic energy equal to
(A) 3J
(B) 5J
(C) 0.5J
(D) 8J
Ques. A body moves a distance of 10m along a straight line under a force of 5N. If work done is 25J, what is the angle between force and direction of motion?
(A) 30°
(B) 45°
(C) 60°
(D) 75°
Ques. The relation between displacement x and time t for a mass 2kg moving under a force is x = 3t³ (x in meters, t in seconds). Work done in 1st 2 seconds is
(A) 1.6J
(B) 16J
(C) 160J
(D) 1600J
Ques. Newton-metre is unit of
(A) Force
(B) Work
(C) Moment of force
(D) Both (B) and (C)
Ques. 10kg rests on frictionless table. Energy needed to accelerate from rest to 5m/s:
(A) 125J
(B) 150J
(C) 175J
(D) 200J
Ques. Potential energy of spring stretched by distance S is 10J. Work needed to stretch additional S is
(A) 30J
(B) 40J
(C) 10J
(D) 20J
Ques. Body moves under machine delivering constant power. Distance moved in time t is proportional to
(A) t1/2
(B) t3/4
(C) t3/2
(D) t2
Ques. Long spring is stretched by 2cm, its PE is V. If spring is stretched by 10cm, PE stored is
(A) 25V
(B) 5V
(C) 5V
(D) 25V
Ques. 1kg stone is tied to end of string 1m. Whirled in vertical circle. Velocity at bottom just sufficient to take to top. What is tension at top (g = 10m/s²)?
(A) Zero
(B) 1N
(C) 10N
(D) 10N
Ques. If KE of body becomes four times initial value, new momentum increases by
(A) 50%
(B) 100%
(C) 125%
(D) 150%
Ques. Bullet in motion hits and embeds in block on frictionless table. What is conserved?
(A) Momentum and KE
(B) KE alone
(C) Neither
(D) Momentum alone
Ques. Bullet of mass m hits target of mass M hanging by string and gets embedded. If block rises to height h, velocity of bullet before collision is:
(A) v = √2gh
(B) v = 2gh[1 + (m/M)]
(C) v = 2gh[1 + (M/m)]
(D) v = 2gh[1 – (m/M)]
Ques. Light and heavy body have equal momentum. Which has greater KE?
(A) Light body
(B) Both have equal KE
(C) Heavy body
(D) Data incomplete
Ques. Particle moving at 5m/s has energy 125J. Its mass is
(A) 10kg
(B) 4kg
(C) 6kg
(D) 25kg
Ques. Mass 2kg projected vertically upwards with speed 3m/s. Maximum gravitational PE is
(A) 18J
(B) 4.5J
(C) 9J
(D) 2.25J
Answers to Assignment
- 0.5J
- 60°
- 16J
- Both (B) and (C)
- 125J
- 30J
- t3/2
- 25V
- Zero
- 100%
- Momentum alone
- v = 2gh[(1 + M/m)]
- The light body
- 10kg
- 9J
Frequently Asked Questions
Work is the energy transferred when a force causes a displacement. For a constant force making an angle θ with displacement d:
W = F · d · cos(θ)
- SI unit: joule (J) = N·m
- Positive work adds energy to the object; negative work removes it.
The net work done on a particle equals the change in its kinetic energy:
Wnet = ΔK = ½ m(vf2 − vi2)
It’s a powerful tool to relate forces/displacements to speeds without tracking time.
- Kinetic Energy (K): energy of motion:
K = ½ m v². - Gravitational Potential Energy (Ug): energy due to height:
U = m g h(near Earth’s surface). - Elastic Potential Energy: for a spring:
U = ½ k x².
Total mechanical energy: E = K + ΣU.
If only conservative forces (like gravity or ideal springs) do work, then
Ki + Ui = Kf + Uf
Non-conservative forces (e.g., friction, air drag) change mechanical energy; the “lost” energy goes to thermal or other forms.
Power is the rate of doing work or transferring energy.
P = dW/dt and for a constant force/velocity along the motion: P = F · v
- SI unit: watt (W) = J/s
- Average power over time Δt:
Pavg = ΔW / Δt
- Work, Energy: joule (J)
- Power: watt (W)
- Positive work/energy: adds mechanical energy; negative: removes it.
- Angles matter: if force is perpendicular to motion (θ = 90°),
W = 0.