Rotational Mechanics

Rigid Body

Rigid Body: A body which cannot be deformed by application of any large force. Practically there is no body which behaves like a rigid body. But each body which we will consider in this chapter is assumed to be a rigid body.

Translation and Rotation of a Rigid Body

Translation of a rigid body

If each particle of the body has equal displacement in same time interval, the motion of the particle will be pure translational.

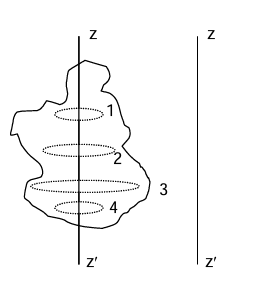
Rotation of a Rigid body

If each particle of a rigid body is moving in a circle, the planes of all circles are parallel to each other, time taken by each particle for one complete revolution is same and centres of each circle are lying on a straight line. The motion is rotation about the straight line and this line is called the axis of rotation.

Sometimes axis passes through the body and some times does not pass through the body.

Kinematics

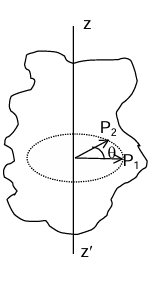
Angular Displacement (θ)

θ = angular displacement. If θ is measured in anticlockwise direction the direction of angular displacement will be towards the observer and perpendicular to the plane of circle and if θ is measured in clockwise direction is going away from the observer and ⊥ to the plane of circles.

Also Read: Kinematics Notes

Angular Velocity (ω)

ω_av = Δθ/Δt = (θ₂ - θ₁)/(t₂ - t₁) ω = Limit_Δt→0 (Δθ/Δt) = dθ/dt = instantaneous angular velocity

Angular Acceleration (α)

α = dω/dt = angular acceleration = d²θ/dt²

Equations of Motion (When α = constant)

ω = dθ/dt Integrating both sides: ∫dω = ∫α dt ω - ω₀ = αt ω = ω₀ + αt ... (i)

∫dθ = ∫ω dt = ∫(ω₀ + αt)dt θ - θ₀

= ω₀t + ½αt² θ = θ₀ + ω₀t + ½αt² ... (ii)

α = dω/dt

= (dω/dθ) × (dθ/dt)

= ω(dω/dθ) ∫α dθ

= ∫ω dω α(θ - θ₀)

= ½(ω² - ω₀²) ω² = ω₀² + 2α(θ - θ₀) ... (iii)

Also Check: Simple Harmonic Motion Notes

Example: A disc starts rotating with constant angular acceleration of π radians/s² about a fixed axis perpendicular shift its plane and through its centre.

Find (a) the angular velocity of the disc after 4 sec. (b) the angular displacement of the disc after 4 sec and (c) number of turns accomplished by the disc in 4 sec.

Solution: Here α = π rad/sec² ω₀ = 0 t = 4 sec (a) ω(4 sec) = 0 + (π rad/sec²) × 4 sec = 4π rad/sec. (b) θ(4 sec) = 0 + ½(π rad/sec²) × (16 sec²) = 8π radian. (c) Let the number of turns be n n × 2π rad = 8π rad ∴ n = 4

Relation between Linear and Rotational Motion

The linear distance along the tangent = s = rθ

Linear speed in tangential direction = v

= Limit_Δt→0 (Δs/Δt) = Limit_Δt→0 (rΔθ/Δt) = r(dθ/dt) = rω Linear acceleration = a = dv/dt = r(dω/dt) = rα

Torque of a Force

Torque about a point about an axis

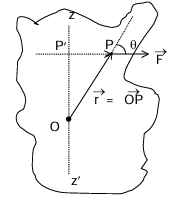
Let us consider any point 'O' on the axis of rotation and other point P on the line of action of force.

Must Read: Heat and Thermodynamics Notes

Torque about point 'O' = r⃗₀ × F⃗

Torque about axis of rotation zz' = τ⃗₀ · n̂

where n̂ = unit vector along the axis. τ₀ = rF sin θ = r⊥ sin θ F = r⊥F

Where r⊥ = OP = distance of the line of action of F⃗ from point 'O' If there are more than one force: τ⃗ = r⃗₁ × F⃗₁ + r⃗₂ × F⃗₂ + ... = Σ τ⃗ₑₓₜ

Example: A particle of mass m is dropped at point A, find the torque about O.

Solution: τ⃗ = r⃗ × F⃗ τ = rF sin θ n̂ = (r sin θ) F n̂ = bmg The direction of torque is directed inward the paper or in other words, rotation about O is clockwise.

Example: A particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.

Solution: At the highest point it has only horizontal velocity vₓ = v cos θ Length of the perpendicular to the horizontal velocity from 'O' is the maximum height, where H_max = (v² sin² θ)/(2g) Angular momentum L = mv cos θ × (v² sin² θ)/(2g) = (mv³ sin² θ cos θ)/(2g)

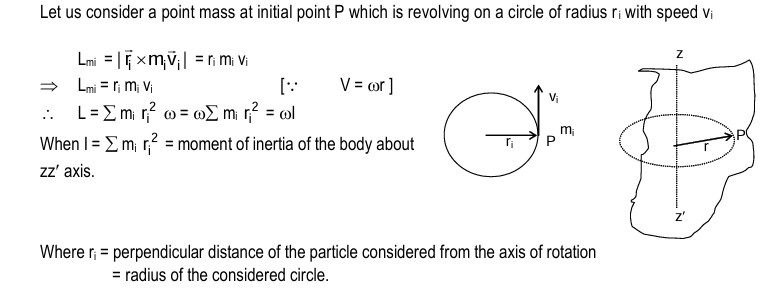
Angular Momentum

Angular momentum of a particle about a point and about an axis

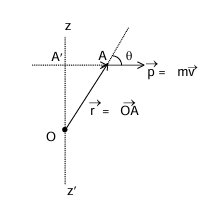
Angular momentum of a rigid body about an axis

Conservation of angular momentum

Angular Impulse

Kinetic Energy of a Rigid Body

Kinetic energy of a rigid body rotating about a given axis

Kinetic energy of a particle of mass mᵢ moving on a circle of radius rᵢ with tangential speed vᵢ is Kᵢ = ½mᵢvᵢ²

Kinetic energy of the body k = Σkᵢ = ½Σmᵢvᵢ²

= ½Σmᵢω²rᵢ²

= ½ω²Σmᵢrᵢ²

= ½Iω²

Where I = Σmᵢrᵢ²

Where rᵢ = ⊥ distance of the particle from the axis of rotation = radius of the considered circle.

Power delivered and work done by a torque

P = dk/dt = d/dt[½Iω²]

= Iω(dω/dt)

= Iωα [I = constant]

P = τω

Calculation of Moment of Inertia

I = Σmᵢrᵢ², for a discrete system of particles and

I = ∫x²dm for a continuous system of particles,

where x = ⊥ distance of elemental mass dm from the axis of rotation.

Physical significance of moment of inertia

Moment of inertia plays same role in rotational motion as mass plays in translational motion. It is the property of the body by which body opposes any change in its state of rotational motion.

Radius of gyration

K = √(I/m) If a particle of same mass is placed at a distance equal to radius of gyration from the axis of rotation the particle will have same moment of inertia as the rigid body has.

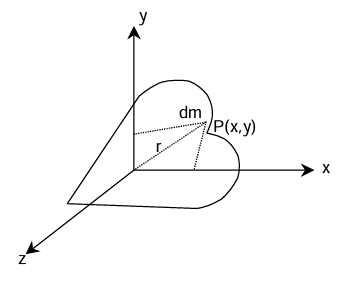
Perpendicular axis theorem

This theorem is applicable for only plane body (not for 3D block). Iₓ = ∫y²dm Iᵧ = ∫x²dm Iₓ + Iᵧ = ∫(x² + y²)dm = ∫r²dm = I_z When x-y plane is along the plane of the body and z axis is perpendicular to it.

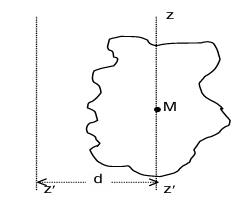
Parallel axis theorem

I = I_CM + md² when m = total mass of the body d = perpendicular distance between the axes I_cm = M.I. about axis passing through centre of mass.

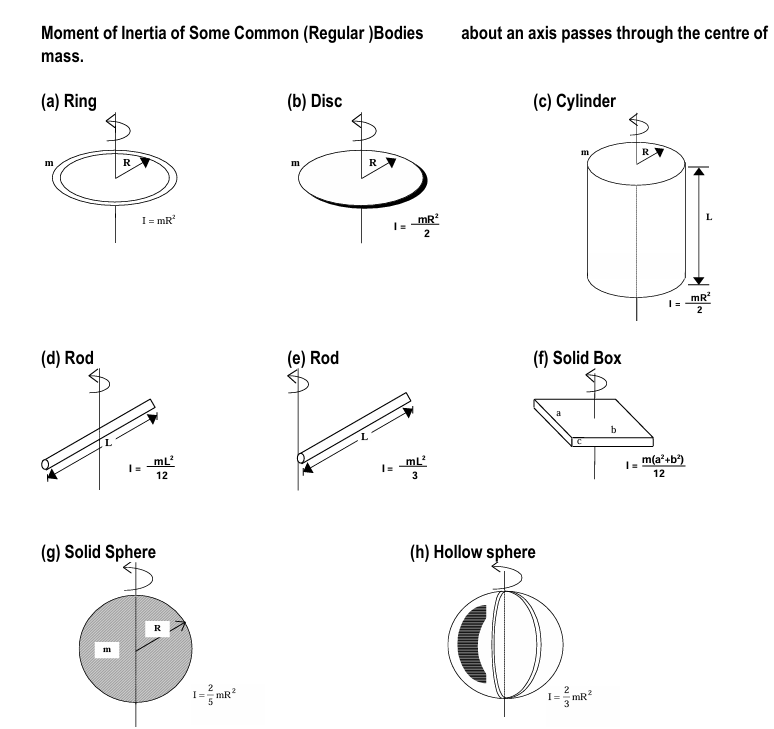
Moment of Inertia of Common Bodies

Object	Moment of Inertia
Ring (about center, perpendicular to plane)	I = mR²
Disc (about center, perpendicular to plane)	I = ½mR²
Cylinder (about axis)	I = ½mR²
Rod (about center, perpendicular)	I = (1/12)mL²
Rod (about end, perpendicular)	I = (1/3)mL²
Solid Box (about center)	I = (1/12)m(a² + b²)
Solid Sphere (about diameter)	I = (2/5)mR²
Hollow Sphere (about diameter)	I = (2/3)mR²

Exercise 1: i) The motor of an engine is rotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assuming constant angular deceleration, calculate the number of revolutions made by it before coming to rest.

ii) Find the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.

More Resources for Class 11 NCERT

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Maths
• NCERT Solutions for Class 11 Biology

Combined Motion (Rotation & Translation)

In this type of motion axis of rotation is not stationary. If a body rotates about an axis with angular frequency ω then with respect to the axis of rotation linear velocity of any particle in the body at a distance r from the axis of rotation is equal to v⃗ = ω⃗ × r⃗ If the axis of rotation also moves with velocity v⃗₀ then net velocity of the particle relative to stationary frame will be v⃗ = v⃗₀ + ω⃗ × r⃗

Example: A cylindrical drum, pushed along by a board rolls forward on the ground. There is no slipping at any contact. Find the distance moved by the man who is pushing the board, when axis of the cylinder covers a distance L.

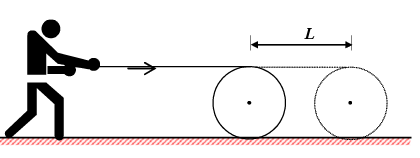
Solution: Let v₀ be the linear speed of the axis of the cylinder and ω be its angular speed about the axis.

As it does not slip on the ground hence ω = v₀/R.

Where R is the radius of the cylinder.

Speed of the topmost point is v = v₀ + ωR = 2v₀

Since time taken by the axis to move a distance L is equal to t = L/v₀.

In the same interval of time distance moved by the topmost point is S = 2v₀ × L/v₀ = 2L

As there is no slipping between any point of contact hence distance moved by the man is 2L.

Exercise 2: i) A uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate (a) the angular momentum of the rod about the axis of rotation. (b) the speed of the centre of the rod and (c) its kinetic energy. (ii) A cylinder rolls on a horizontal plane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?

Angular Momentum of a Body with Both Translational and Rotational Motion

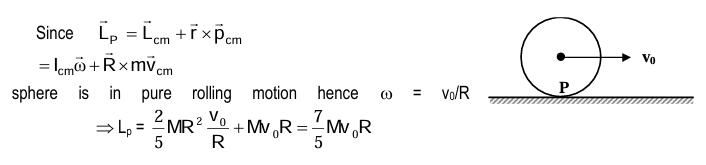
Example: A sphere rolls without slipping on a rough surface with centre of mass having constant speed v₀. If mass of the sphere is m and its radius be R, then find the angular momentum of the sphere about the point of contact.Solution: image

Solutions: 

Kinetic Energy Of A Rolling Body

Kinetic energy of a rolling body is given by

K = ½I_cmω² + ½Mv²_cm

= ½I_cmω² + ½MR²ω²

= ½(I_cm + MR²)ω²

Role Of Friction In Rolling Motion

• If a body rolls without slipping such that velocity of its centre of mass does not change then no frictional force acts on the body.
• However, If a force acts on the body, which changes the velocity of its centre of mass or its angular velocity about the centre then there is a tendency of the body to slide at the point of contact and hence frictional force acts on the body to oppose this tendency.

Formulae and Concepts at a Glance

1. I = Σm_ir_i² = MK²

2. K = √(Σr_i²/n)

3. According to theorem of parallel axes, I_AB = I_C + Mh²

4. According to theorem of perpendicular axes I_z = I_x + I_y

5. For a uniform circular ring, moment of inertia about an axis passing through the centre and perpendicular to the plane of the ring, I = MR²

6. For a uniform circular disc, I = ½MR²

7. For a thin uniform rod, I = (1/12)ML²

8. Moment of inertia of a hollow cylinder about its axis = MR²

9. Moment of inertia of a solid cylinder about its axis = ½MR²

10. Moment of inertia of a hollow sphere about its diameter = (2/3)MR²

11. Moment of inertia of a solid sphere about its diameter = (2/5)MR²

12. K.E. of rotation = ½Iω²

13. K.E. of translation = ½mv²

14. Total K.E. = ½Iω² + ½mv²

15. Angular momentum = Iω

16. Torque τ = Iα

17. Relation between torque and angular momentum τ = dL/dt

18. Power of a torque P = τω

19. Acceleration of a point mass tied to the string wound on a cylinder a = g/(1 + I/mR²)

20. Tension in the string, T = mg/(1 + mR²/I)

21. Acceleration of a body rolling down a rough inclined plane of inclination θ is a = mg sin θ/(m + I/r²)

22. Coefficient of friction for rolling of solid cylinder without slipping down the rough inclined plane is μ = (1/3)tan θ

Solved Problems

Problem 1: A rod of length 1m and mass ½ Kg rotates at an angular speed of 6 rad/s about one of its ends. The kinetic energy of the rod is

(A) 4J

(B) 3J

(C) 2.5J

(D) 1.5J