Simple Harmonic Motion

If a motion repeats itself in equal intervals of time, it is said to be periodic motion. The displacement of a particle in such motion can always be expressed in terms of sines and cosines therefore periodic motion is often called harmonic motion.

Examples:

• Rotation of earth about its axis
• Revolution of moon around the earth
• Vibration of spring

OSCILLATORY MOTION

When a particle executes to and fro motion about some fixed point, its motion said to be oscillatory or vibratory.

Examples of oscillatory motion:

• The motion of the bob of a pendulum
• Mass attached to a spring
• Violin strings
• Atoms in a solid lattice
• Air molecules as a sound wave passes by

Solution of the Equation of SHM

The necessary and sufficient condition for a motion to be simple harmonic is that the net restoring force (or torque) must be linear i.e.

F = ma = -kx (Where k is a constant)

⇒ a = d²x/dt² = -(k/m)x

where x is the instantaneous displacement. Multiplying both sides by dx/dt and integrating with respect to t,

We get

(1/2)(dx/dt)² = -(k/2m)x² + C ... (i)

Where C is a constant of integration. Now when x is maximum dx/dt will be zero. The maximum displacement x_max of the particle from the mean position is called amplitude and is represented by A, then the value of C comes out to be

C = (kA²)/(2m)

Hence

(1/2)(dx/dt)² = (k/2m)(A² - x²)

Putting k/m = ω² we get

dx/dt = ω√(A² - x²) ... (ii)

This equation gives the velocity of the particle in S.H.M. again

dx/√(A² - x²) = ωdt ... (iii)

Integrating this equation with respect to t. we get

sin⁻¹(x/A) = ωt + φ

Where φ is another constant of integration which depends on initial conditions.

Thus

x = A sin (ωt + φ) ... (iv)

With the change of time t, sin (ωt + φ) varies between 1 and –1 and corresponding displacement x varies between A and –A. Thus the range of vibration is 2A. The term (ωt + φ) represents total phase of the particle at any instant t,

Here ω is called as angular velocity the rate of change of phase angle of the particle with time and φ is called phase constant or initial phase, its value depends upon initial conditions. If the time is recorded from the instant when x is zero and is increasing then according to equation (iv) φ must be equal to zero.

Now the periodic time or time required to complete one vibration or the time to increase the phase angle of the particle by 2π is given by

T = 2π/ω = 2π√(m/k) ... (v)

T is called the time period of oscillation.

The frequency f, the number of complete vibration per second is given by

f = 1/T = (1/2π)√(k/m) ... (vi)

If we put π/2 + φ in place of φ then

x = A cos (ωt + φ) ... (vii)

Thus S.H.M. may also be represented by a cosine function but initial phase is different in two cases.

Projection of Uniform Circular Motion on a Diameter

Let at t = 0 the particle is at the point A and after time t it is at B. The foot of the perpendicular from the point on the diameter oscillates about O which is S.H.M. in nature.

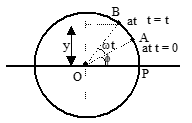
A circle with center O, point A at t=0, point B at t=t, with projection P on diameter showing oscillatory motion

The displacement of the projection from centre is given by

y = R sin(ωt + φ)

The maximum displacement of the projection from the centre is called amplitude. If amplitude is denoted by A, then R = A.

⇒ y = A sin(ωt + φ) ... (ii)

Problem 1 : A small particle is kept on a smooth concave glass of radius of curvature R placed on a horizontal table. Show that if the particle is displaced from the mean position and left, it executes simple harmonic motion, and find its period. (displacement being very small compared to R.).

Solution: O is the centre of curvature of the glass. The equilibrium position of the particle is at A with OA as the vertical. If displaced, it will oscillate to and fro about the equilibrium position.

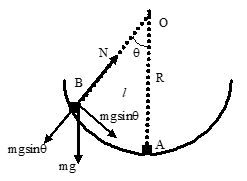
Concave surface with center O, particle at position B displaced by angle θ from equilibrium position A, showing forces mg and N

Let B be the position of the particle at any time, so that AB = x and ∠BOA = θ. The forces acting on the particle will be:

(a) its weight mg acting vertically downwards

(b) the normal reaction N along BO

Resolving the weight mg into components along the normal to the surface and perpendicular to it, the component mg sinθ directed towards the mean position provides the restoring force.

∴ Restoring force = F = mg sinθ

∴ Acceleration = a = -g sinθ (-ve sign to indicate that acceleration is opposite in direction to the displacement).

= -g θ (∵ θ = x/R is very small) = -g(x/R)

∴ The motion of the particle is a S.H.M..

∴ Acceleration = -ω²x = -(g/R)x

ω² = g/R

ω = √(g/R)

Period oscillation = T = 2π/ω = 2π√(R/g)

Note: This is equivalent to a simple pendulum of length = R

Since this method is made use of to determine the radius of curvature of the surface, this is called 'dynamical spherometer'.

Characterstics of SHM

Displacement (x):

If time is measured from the equilibrium position, displacement x from equilibrium point at any instant of time t is given by x = A sinωt

Velocity (v):

v = dx/dt = d/dt(A sinωt) = Aω cosωt

or

v = Aω√(1 - sin²ωt) = ω√(A² - x²)

(i) Velocity is minimum at extreme positions and is zero.

at x = ±A, v = v_min = zero.

(ii) Velocity is maximum at the equilibrium position and is Aω.

at x = 0, v = v_max = Aω

(iii) Direction of velocity is either towards or away from the equilibrium position.

Acceleration (a):

a = dv/dt = d²x/dt² = -ω²A sinωt = -ω²x

(i) The minimum value of acceleration is zero and it occurs at equilibrium, a_min = 0.

(ii) The maximum value of acceleration is ω²A and it occurs at extreme positions, a_max = ω²A

(iii) Acceleration is always directed towards the equilibrium position and so is always opposite to displacement.

Energy of a body in SHM

In general the total energy of a harmonic oscillator consists of two parts, potential energy (P.E) and Kinetic Energy (K.E.), the former being due to its displacement from the mean position and later due to its velocity. Since the position and velocity of the harmonic oscillator are continuously changing, P.E. and K.E. also change but their sum i.e., the total energy (T.E) must have the same value at all times.

Potential Energy

The linear restoring force acting on the harmonic oscillator is given by

F = m(d²x/dt²) = -kx

Now if the oscillator is displaced through a further displacement dx against the force, work done in displacing the particle is given by

dW = kx dx

Hence the total work done in displacing the particle from mean position (x = 0) to (x = x) is given by

W = ∫₀ˣ kx dx = (1/2)kx²

As P.E. at the mean position is taken zero, the above equation gives the values of P.E. of harmonic oscillator at a displacement x from the mean position i.e.,

U = (1/2)kx² = (1/2)mω²x² ... (1)

This shows the P.E. is proportional to the square of the displacement and graph showing the variation of potential energy with the displacement will be a parabola given by continuous line in the figure. P.E. is maximum at maximum displacement and is given by

U_max = (1/2)mω²A²

Kinetic Energy

Velocity of harmonic oscillator is given by equation as

V = dx/dt = ω√(A² - x²)

Hence Kinetic energy T of the oscillator is given by

T = (1/2)mv² = (1/2)mω²(A² - x²) ... (2)

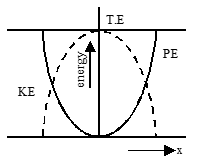
Shows parabolic curves for KE, PE, and constant line for Total Energy vs displacement

The kinetic energy is maximum when x = 0. Thus

T_max = (1/2)mω²A²

Now total energy E of the oscillator for displacement x is given by

E = P.E. + K.E. = (1/2)mω²x² + (1/2)mω²(A² - x²) = (1/2)mω²A² ... (3)

Thus total energy is independent to the displacement, it remains constant throughout the motion of the oscillator. It is being represented by a straight line parallel to displacement axis in figure. Also the total energy is equal to maximum value of either P.E. or K.E.

Average Value of PE and KE

By equation (1) P.E. at distance x is given by

U = (1/2)mω²x² = (1/2)mω²A² sin²(ωt)

The average value of P.E. for complete vibration is given by

U_average = (1/T)∫₀ᵀ U dt = (1/T)∫₀ᵀ (1/2)mω²A² sin²(ωt) dt

= (mω²A²/4T)∫₀ᵀ 2sin²(ωt) dt = (1/4)mω²A²

because the average value of sine or of cosine function for the complete cycle is equal to zero.

Now K.E. at x is given by

T = (1/2)m(dx/dt)² = (1/2)m(d/dt[A sin(ωt)])² = (1/2)mω²A² cos²(ωt)

The average value of K.E. for complete cycle

T_average = (1/T)∫₀ᵀ (1/2)mω²A² cos²(ωt) dt = (mω²A²/4T)∫₀ᵀ{1 + cos2(ωt)} dt = (mω²A²/4T) · T = (1/4)mω²A²

Thus average values of K.E. and P.E. of harmonic oscillator are equal and each to half of the total energy

Problem: If a SHM is represented by the equation x = 10 sin [ωt + π/6] in S. I. Units Determine its amplitude, time period and maximum velocity?

Solution: Comparing the above equation with x = A sin (ωt + φ₀), we get,

• A = 10 m
• ω = ω s⁻¹ and φ₀ = π/6
• ∴ T = 2π/ω
• ∴ T = 2s
• v_max = ωA = 10ω m/s.

Problem: A particle executes S.H.M.

(a) What fraction of total energy is kinetic and what friction is potential when displacement is one half of the amplitude.

(b) At what displacement the kinetic and potential energies are equal.

Solution: We know that

E_total = (1/2)mω²A²
K.E. = (1/2)mω²(A² – x²) and U = (1/2)mω²x²

(a) when x = A/2

K.E. = (1/2)mω²(A² - A²/4) = (3/4) · (1/2)mω²A² ⇒ K.E./E_total = 3/4

At x = A/2, U = (1/2)mω² · A²/4 ⇒ P.E./E_total = 1/4

(b) Since K = U

(1/2)mω²(A² – x²) = (1/2)mω²x²
or 2x² = A² or x = A/√2 = 0.707A

Simple Pendulum

A heavy small mass (bob) suspended by a light, long and inextensible string forms simple pendulum.

Length of the simple pendulum is the distance between the point of suspension and the centre of mass of the suspended mass.

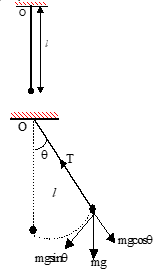
Showing bob suspended from point O, displaced by angle θ, with forces T and mg acting on it

Consider the bob when string deflects through a small angle θ.

Force acting on the bob are tension T in the string and weight mg of the bob. Torque on the bob about point O is

τ = mgl sinθ + T·0 = mgl sinθ ≈ mglθ as θ is very small ... (1)

M.I. of the bob about the point O is

I = ml²

Hence

τ = ml² d²θ/dt² ... (2)

As torque and θ are oppositely directed hence from (1) and (2), we get

ml² d²θ/dt² = -mglθ

d²θ/dt² = -(g/l)θ

Comparing with the equation d²x/dt² = -ω²x, we get

ω = √(g/l)

Since T = 2π/ω

∴ T = 2π√(l/g)

Note: If simple pendulum is made to oscillate in non inertial frame of reference. Then torque due to pseudo force must be taken in account.

Exercise 2:

Ques 1. Which is wrong

• A particle executes SHM between X=-A and X = +A the time take for it to go from 0 to A/2 is T₁ and to go from A/2 to A is T₂ then, T₁ < T₂
• in a SHM, X = 3sin 3πt/4 + 4cos3πt/4, x is in metres, then amplitude of the motion is 5m.
• Graph between restoring force and displacement in SHM is linear through origin
• A particle executes SHM with amplitude 0.1M, the distance from the mean position whose the ice and PE be comes equal is 0.05√2 sec

Ques 2. The bob of a simple pendulum is a hollow sphere filled with a liquid. As the pendulum oscillates the liquid drips through a hole at the bottom of the bob. How will the time period vary as the liquid drips?

Ques 3. When two mutually perpendicular SHM of same amplitude and same frequency are super imposed then the resultant curried path is called Lissajous Figures. What will be shape of Lissajous figures when.....

• Phase difference between two SHM are 0, π/4, π/2, 3π/4, π
• In above if amplitude are not equal, then shapes will be.
• In above if frequency ratio is not exactly equal to one. Than shapes will be.
• When ratio of frequencies is 2, then shapes will be.

Physical Pendulum

Any rigid body suspended from a fixed support constitutes a physical pendulum.

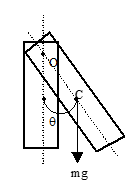
Rigid body suspended from point O, with center of mass C at distance l, displaced by angle θ

Consider the situation when the body is displaced through a small angle θ. Torque on the body about o is given by

τ = mgl sinθ ... (1)

where l = distance between point of suspension and centre of mass of the body.

If I be the M.I. of the body about O.

then τ = I d²θ/dt² ... (2)

From (1) and (2), we get

I d²θ/dt² = -mgl sinθ ⇒ d²θ/dt² = -(mgl/I)θ since θ is very small.

Comparing with the equation d²θ/dt² = -ω²θ, we get

ω = √(mgl/I)

Since T = 2π/ω

⇒ T = 2π√(I/mgl)

Equivalent Simple Pendulum

A simple pendulum whose time period is same as that of a physical pendulum is called the equivalent simple pendulum of the given physical pendulum.

Then

T = 2π√(l/g) = 2π√(I/mgd) ⇒ l = I/md

This is called the length of equivalent simple pendulum.

Oscillation of Spring

A point mass suspended from a massless spring constitutes a linear harmonic spring pendulum. But in reality neither point mass nor massless spring exists.

Restoring force in spring pendulum due to elasticity of spring.

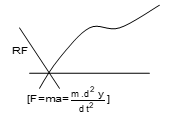
Shows relationship between restoring force RF and displacement

RF = ky – ky² + cy³

For small displacement RF = -ky

K = spring constant.

m(d²y/dt²) = -ky
d²y/dt² = -(k/m)y = -ω²y

Time period

T = 2π√(m/k)

∴ T is independent of gravity (Clocks based on spring pendulum)

Exercise 3:

Ques 1. Choose the wrong statement

• A simple pendulum of length (l) is suspended from root of a train which moves in a horizontal direction with an acceleration a then the time period (T) is 2π√(l/√(a² + g²))
• If spring is extended to length (l), then according to hookes law. F = kl
• A simple pendulum of length L has period T on earth and Ts in a satellite then Ts > T.

Ques 2. Why is the physical pendulum more accurate then a simple pendulum?

Solved Problems

Question: A particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillations is

(A) 3T/8

(B) 5T/8

(C) 5T/12

(D) 7T/12

Solution:

Time to complete 1/4 th of the oscillations of T/4 s.

Time to complete 1/8 th vibration means when the vibrating particle reaches from the extreme position to the half the amplitude

⇒ y = A/2 = A sin(ωt + π/2) = A cosωt ⇒ t = T/6 s

∴ Total time required = T/4 + T/6 = 5T/12

Answer: (C)

Question: The motion of a particle varies with time according to the relation y = a (sinωt + cosωt)

(A) the motion of oscillatory but not SHM.

(B) the motion is SHM with amplitude a.

(C) the motion is SHM with amplitude a√2.

(D) the motion is SHM with amplitude 2a.

Solution:

y = a (sinωt + cosωt)

= a√2 [(1/√2)sinωt + (1/√2)cosωt]

= a√2 sin(ωt + π/4)

∴ The motion is S.H.M. in nature and has an amplitude a√2.

Answer: (C)

Question: The displacement of a particle executing SHM is given by y = 0.25sin200t cm. The maximum speed of the particle is

(A) 200 cm/sec

(B) 100 cm/sec

(C) 50 cm/sec

(D) 5.25 cm/sec

Solution:

In the given question y = 0.25sin200t

Speed v = dy/dt = 0.25×200 cos200t

∴ maximum speed = 0.25×200 = 50 cm/s

Answer: (C)

Question: A mass suspended from a massless spring stretches it by a distance y. If pulled slightly more and let go, it will oscillate with a time period T where

(A) T = 2π√(y/g)

(B) T = 2π√(y/mg)

(C) T = 2π√(g/y)

(D) T = π√(y/g)

Solution:

The restoring force is going by ky = mg

or k/m = g/y

∴ T = 2π√(m/k) = 2π√(y/g)

Answer: (A)

Question: A particle is vibrating in SHM with an amplitude of 4 cm. At what displacement from the equilibrium position is its energy half potential and half kinetic

(A) 1cm

(B) 2 cm

(C) 2√2 cm

(D) 2√2 cm

Solution:

According to the question given

(1/2)mω²y² = (1/2)mω²(a² - y²)

or 2y² = a²

or y = a/√2 = 4/√2 = 2√2 cm

Answer: (D)

Assignment

Ques 1. A particle executes S.H.M. Then the graph of velocity as a function of displacement is

• a straight line
• a circle
• an ellipse
• a hyperbola

Ques 2. A pendulum is undergoing SHM. The velocity of the bob in the mean position v. if now its amplitude is doubled, keeping the length same, its velocity in the mean position will be

• v/2
• v
• 2v
• 4v

Ques 3. A particle executes S.H.M. along a straight line so that its period is 12 sec. The time it takes in traversing a distance equal to half its amplitude from its equilibrium is

• 6 sec
• 4sec
• 2 sec
• 1 sec

Ques 4. The time period of a particle undergoing S.H.M. is 16 sec. it starts motion from the mean position. After 2 sec, its velocity is 0.4 m/s. The amplitude is

• 1.44 m
• 0.72 m
• 2.88 m
• 0.36

Ques 5. A tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period

• 42 minutes
• 1 day
• 1 hours
• 84.6 minutes

Ques 6. The maximum speed of a particle executing S.H.M. is 1 m/s and maximum acceleration is 1.57 m/s². Its time period is

• 4 sec
• 2 sec
• 1.57 sec
• 1/1.57 sec

Ques 7. The velocity-time diagram of a harmonic oscillator is shown in figure. The frequency of oscillation is

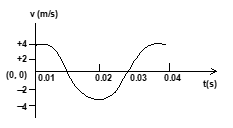
• 25 Hz
• 12.25 Hz
• 50 Hz
• 33.3 Hz

Ques 8. Starting from y = A sinωt or y = A cosωt

• acceleration lags the displacement by a phase π/4.
• acceleration lags the displacement by a phase π/2.
• acceleration leads the displacement by a phase π/2.
• acceleration leads the displacement by a phase π.

Ques 9. In the above question, acceleration

• lags the velocity by a phase π/4.
• leads the velocity by a phase π/2.
• leads the velocity by a phase π.
• leads the displacement by a phase π.

Ques 10. The time taken by a particle executing SHM of periodic T to move from the mean position to half the maximum displacement is

• T/3
• T/4
• T/8
• T/12

Ques 11. A particle moves such that its acceleration 'a' is given by a = -bx where x is the displacement from equilibrium position and b is constant. The period of oscillation is

• 2π/√b
• 2π/√b
• 2π√b
• 2π√b

Ques 12. The bob of a simple pendulum of length L is released at time t =0 from a position of small angular displacement. Its linear displacement at time t is given by

• x = a sin²√(g/L)t
• x = a cos²√(L/g)t
• x = a sin√(L/g)t
• x = a cos√(L/g)t

Ques 13. The acceleration d²x/dt² of a particle varies with displacement x as d²x/dt² = -Kx where K is a constant of the motion. The time period T of the motion is equal to

• 2π√K
• 2π√K
• 2π/√K
• 2π/√K

Ques 14. Which one of the following equations does not represent SHM? x = displacement and t = time. Parameters a, b and c are the constants of motion

• x = a sinbt
• x = cosbt + c
• x = asinbt + c cosbt
• x = a secbt + c cosecbt.

Ques 15. Two identical blocks P and Q have mass m each. They are attached to two identical springs initially in stretched. How the left spring (along with P) is compressed by A/2 and the right spring (along with Q) is compressed by A. Both the blocks are referred simultaneously. They collide perfectly in elastically. Initially time period of both the block was T. Choose correct option for time period, amplitude, energy of combined mass.

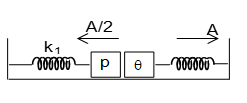
• √2T, 3A/4, kA²/16
• T, A/4, kA²/16
• T, 3A/4, kA²/16
• √2T, 3A/4, kA²/4

Answers to Assignment

1. C

2. C

3. D

4. A

5. D

6. A

7. A

8. D

9. B, D

10. D

11. B

12. C

13. C

14. D

15. B