Gravitation

NEWTON'S LAW OF GRAVITATION

After studying the observations of previous astronomers and making his own studies, Newton came to the conclusion that: Newton's Universal Law of Gravitation "Every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them".

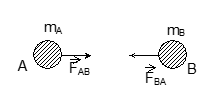
Diagram: Two particles A and B attracting each other

[Two masses m_A and m_B separated by distance d_AB with force vectors F_AB and F_BA]

Consider two particles A and B of masses m_A and m_B, attracting each other with forces F_AB (force on A due to B) and F_BA (force on B due to A) respectively.

Mathematical Expression

F = G × (m₁m₂)/d²

Where:
• F = magnitude of the attractive force
• G = Universal gravitational constant
• m₁, m₂ = masses of the two particles
• d = distance between them

Universal Gravitational Constant

• Value of G: G = 6.6726 × 10^-11 N⋅m²/kg²
• Dimensions of G: [M^-1L³T^-2]
• First measured by: Cavendish (1798)

Properties of Gravitational Forces

• Gravitational forces are like ordinary forces, except that they act at a distance
• Gravitational forces obey the superposition principle
• They are always attractive in nature
• They are central forces (act along the line joining the centers)

Superposition Principle

The net gravitational force on a particle A due to particles P₁, P₂, ……, P_n is given by:

F_net = F₁ + F₂ + F₃ + ... + F_n (vector sum)

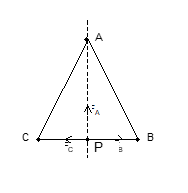
Illustration: Three Identical Particles

Problem: Three identical particles each of mass m are placed at three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at:

(a) the mid-point of a side

(b) at the centre of the triangle

Solution:

Using principle of superposition, the force on the particle due to charged particles placed at the corner of the triangle.

(a) When the particle is placed at the mid point of a side (at P):

The forces from the two adjacent corners have equal magnitudes and their components perpendicular to the side cancel each other.

Net Force = Gm²/a² × (√3/2) towards the third vertex

(b) At the centre of the triangle:

The net force on the particle at P due to particles placed at corners A, B and C will be zero due to symmetry.

F_net = 0

GRAVITATIONAL FIELD AND INTENSITY

Gravitational Field: The region of space where the gravitational force of a particle A acts on any other particle is known as the gravitational field of the particle A.

Gravitational Field Intensity

The intensity of gravitational field at a point (P) is given by the force per unit mass on a test particle kept at the point P:

I = F⃗/m₀

Where:
• I = Gravitational field intensity
• F⃗ = Gravitational force acting on mass m₀ at P
• m₀ = Test mass

Field Intensity Due to Point Mass

The gravitational field at P of a particle of mass m kept at the origin O is given by:

I⃗ = -Gm/r² × r̂

Where:
• r⃗ = position vector of point P with respect to source O
• r̂ = unit vector along radial direction

Unit: N/kg or m/s²

Dimensions: [M⁰LT⁻²]

Superposition for Field Intensity

The gravitational field intensity at point P due to multiple sources:

I_P = I₁ + I₂ + I₃ + ... (vector sum)

Important Note: The gravitational field at point P depends only upon the sources and does not depend on the test mass m₀ used to measure the field at P.

GRAVITATIONAL FIELD POTENTIAL AND POTENTIAL ENERGY

Conservative Force: The gravitational force is a conservative force and accordingly the force field is a conservative force field.

Conservative Nature of Gravitational Force

For a conservative force field:

∮ F⃗ · dl⃗ = 0 (for a closed path)

Mathematical Proof

Let's show it for a single particle:

F⃗ = -Gmm₀/r³ × r⃗ ...(1)

= -Gmm₀/r² × r̂ ...(2)

Where r⃗ is the radius vector of the point P(x, y, z), the position of a particle of mass m₀, the source being a particle of mass m at O.

F⃗ · dl⃗ = -Gmm₀/r³ × (xdx + ydy + zdz) ...(3)

Since r² = x² + y² + z², we have:

2r dr = 2xdx + 2ydy + 2z dz ...(4)

Therefore:

F⃗ · dl⃗ = -Gmm₀/r² dr = +Gmm₀ d(1/r) ...(5)

Key Result: The work done by the gravitational force in moving a particle from P to Q does not depend on the path, only on the distance of the initial and final points from the sources.

Gravitational Potential Energy

As we know potential energy is negative of the work done by conservative force:

Gravitational Potential Energy = -∫ F⃗ · dl⃗

Definition: It is defined as the gravitational potential energy per unit mass at a point.

V = U/m = -GM/r
Where:
• V = Gravitational potential
• U = Gravitational potential energy
• m = mass of the object
• M = source mass
• r = distance from source

Relation Between Field and Potential

I⃗ = -∇V = -dV/dr × r̂

Exercise 1:

1. (i) Force of gravity acts on all bodies in proportion to their masses, why doesn't a heavy body fall correspondingly faster than light body?
2. (ii) What is the significance of the negative sign in gravitational potential energy?

Illustration: Gravitational Potential Problem

Problem: At a point above the surface of earth, the gravitational potential is -5.12 × 10⁷ J/kg and the acceleration due to gravity is 6.4 m/s². Assuming the mean radius of the earth to be 6400 km, calculate the height of this point above the earth's surface.

Solution:

Let r be the distance of the given point from the centre of the earth. Then:

Gravitational potential = -GM/r = -5.12 × 10⁷ ...(i)

Acceleration due to gravity, g = GM/r² = 6.4 ...(ii)

Dividing (i) by (ii), we get:

r = (-5.12 × 10⁷)/6.4 = 8 × 10⁶ m = 8000 km

Height of the point from earth's surface:

h = r - R = 8000 - 6400 = 1600 km

ESCAPE VELOCITY

Escape Velocity: Escape velocity on the surface of earth is the minimum velocity given to a body to make it free from gravitational field i.e. it can reach at infinite distance.

Derivation of Escape Velocity

Let v_e be the escape velocity of the body on the surface of earth and the mass of the body to be projected be m. Now conserving energy at the surface of the earth and infinity:

Initial Energy = Final Energy
½mv_e² - GMm/R = 0 + 0

v_e = √(2GM/R)

Alternative Expression

Since g = GM/R², we can write:

v_e = √(2gR)

For Earth: v_e = 11.2 km/s

Exercise 2:

1. (i) What will be the escape velocity of a body if it is projected at 45° to the horizontal?
2. (ii) Why are the lighter gases rare on the surface of the earth?
3. (iii) If a projectile is fired straight up from the earth's surface, what will happen if the total mechanical energy (a) less than zero? (b) greater than zero? Ignore air resistance and effects of other heavenly bodies.

Illustration: Escape Velocity of Jupiter

Problem: Jupiter has mass 318 times that of earth, and its radius is 11.2 times the earth's radius. Estimate the escape velocity of a body from Jupiter's surface given the escape velocity from the earth's surface as 11.2 km/s.

Solution:

Given: M_J = 318 M_e; R_J = 11.2 R_e; v_e = 11.2 km/s

We know:

v_J = √(2GM_J/R_J) and v_e = √(2GM_e/R_e)

Therefore:

v_J/v_e = √[(M_J/M_e) × (R_e/R_J)]
v_J = v_e × √(318/11.2) = 11.2 × √28.4 ≈ 59.7 km/s

GRAVITATIONAL SELF ENERGY

Gravitational Self Energy: It is defined as the potential energy of the body due to its mass content. It is equal to the work done in the formation of the body from infinitesimal fractions of its mass placed at infinite distances.

If the body is considered to be made of N discrete particles then like potential energy of a system of masses, the total self energy of the body may be expressed as:

U = -G Σ Σ (m_im_j)/r_ij (i≠j)

MOTION OF PLANETS AND SATELLITES

One of the greatest ideas proposed in human history is the fact that the earth is a planet, among other planets, that orbit the sun. The precise determination of these planetary orbits was carried out by Johannes Kepler, using the data compiled by his teacher, the astronomer Tycho Brahe.

Kepler's Laws of Planetary Motion

Kepler's Three Laws:

1. Law of Orbits: Each planet moves in an elliptical orbit, with the sun at one focus of the ellipse
2. Law of Areas: A line from the sun to a given planet sweeps out equal areas in equal times
3. Law of Periods: The square of the periods of the planets are proportional to cube of their mean distance from the sun

Diagram: Planet revolving around the Sun in circular orbit

[Planet of mass m orbiting Sun of mass M in circular orbit of radius r with velocity v]

Derivation for Circular Orbits

Consider a planet of mass m, rotating around the sun (mass M, M>>m) in a circular orbit of radius r with velocity v.

By applying Newton's law of gravitation and the second law of motion:

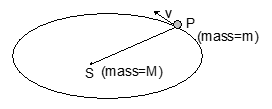
Gravitational force = mass × centripetal acceleration
GMm/r² = mv²/r

v² = GM/r ...(2)

Time Period of Orbit

The time period of rotation, T, of the planet around the sun is given by:

T = 2πr/v = 2πr/√(GM/r) = 2π√(r³/GM) ...(3)

Squaring both sides:

T² = (4π²/GM) × r³ ...(4)

This is Kepler's 3rd Law of Motion

Note that the constant of proportionality depends only on the mass of the sun (M) but not on the mass of the planet.

Important: Kepler's Laws are also valid for the motion of satellites around the earth.

KEPLER'S 2ND LAW AND ITS MEANING

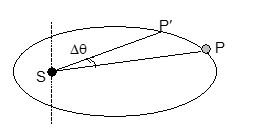
[Elliptical orbit showing planet positions P and P' with swept area ΔA in time Δt]

Consider a planet P that moves in an elliptical orbit around the sun, and let P and P' be the positions of the planet at time t and t+Δt (where Δt is a very small time interval). If the angular displacement of the planet is Δθ, then the area swept out by the line joining the planet SP in time Δt is:

ΔA = area of the section = ½r²Δθ

where r = the length SP

Areal Velocity

v_A = ΔA/Δt = ½r²(Δθ/Δt) = ½r²ω = constant ...(5)

Connection to Angular Momentum

According to Kepler's 2nd law, we have:

mr²(dθ/dt) = mr²ω = constant

This is the expression for the angular momentum of the planet:

L = Iω = mr²ω = mr²(dθ/dt) = constant ...(6)

The gravitational force F⃗ = GMm/r² × r̂ is centripetal, and the torque on the planet is zero:

τ⃗ = r⃗ × F⃗ = 0 ...(7)

Key Points:

• The angular momentum of the planet does not vary
• The areal velocity of the planet remains constant
• At aphelion (farthest point from sun, r is large) the planet moves slowly
• At perihelion (nearest point from sun, r is small) the planet moves fastest

Illustration: Saturn's Distance from Sun

Problem: A Saturn year is 29.5 times the earth year. How far is Saturn from the sun if the earth is 1.5 × 10⁸ km away from the sun?

Solution:

Given: T_S = 29.5 T_e; R_e = 1.5 × 10¹¹ m

According to Kepler's third law:

T²₁/T²₂ = R³₁/R³₂

R_S = R_e × (T_S/T_e)^(2/3)
R_S = 1.5 × 10¹¹ × (29.5)^(2/3)
R_S = 1.43 × 10¹² m = 1.43 × 10⁹ km

Illustration: Angular Momentum of Planet in Elliptical Orbit

Problem: A planet of mass m moves along an ellipse around the sun so that its maximum and minimum distances from the sun are equal to R and r respectively. Find the angular momentum of this planet relative to the centre of the sun.

Solution:

According to Kepler's Second Law, the angular momentum of the planet is constant:

mv₁R = mv₂r → v₁R = v₂r

If the mass of the Sun is M, conserving total mechanical energy at the two positions:

½mv₁² - GMm/R = ½mv₂² - GMm/r

Solving these equations:

Angular momentum = mv₁R = m√[2GMrR/(R+r)]

ORBITAL VELOCITY

Orbital Velocity: When a satellite revolves in an orbit around a planet it requires centripetal force to do so. This centripetal force is provided by the gravitational force between the planet and the satellite.

Derivation of Orbital Velocity

If the mass of the satellite is m and that of the planet is M, then the gravitational force between them at a height h above the surface of the planet is:

F = GMm/(R+h)²

where R is the radius of the earth.

If the speed of the satellite in its orbit (R + h) is v, then the required centripetal force is:

F_c = mv²/(R+h)

Equating the two forces:

GMm/(R+h)² = mv²/(R+h)

v = √[GM/(R+h)]

For Low Earth Orbits

If the height is very small compared to the radius of the earth (h << R), then:

v = √(GM/R) = √(gR)

Geostationary Satellites

If the time period of the satellite is 24 hrs rotating in the same sense as the rotation of the earth, and if the plane of the orbit is at right angle to the polar axis of the planet (earth), then the satellite will always be above a certain place on earth.

This kind of satellites are called geostationary satellites.

Illustration: Artificial Satellite Problem

Problem: An artificial satellite of mass 100kg is in circular orbit at 500 km above the earth's surface. Take the radius of the earth as 6.5 × 10⁶ m.

(a) Find the acceleration due to gravity at any point along the satellite path.

(b) What is the centripetal acceleration of the satellite?

Solution:

Given: h = 500 km = 0.5 × 10⁶ m, R = 6.5 × 10⁶ m

r = R + h = 6.5 × 10⁶ + 0.5 × 10⁶ = 7.0 × 10⁶ m

(a) Acceleration due to gravity:

g' = g(R/r)² = 9.8 × (6.5/7.0)² = 8.45 m/s²

(b) Centripetal acceleration:

a = GM/r² = g'= 8.45 m/s²

ACCELERATION DUE TO GRAVITY AND ITS VARIATION

[Spherical Earth with radius R ≈ 6400 km and mass M ≈ 5.77 × 10²⁴ kg]

Consider the earth as a sphere of radius R (≈ 6400 km) and mass, M (≈ 5.77 × 10²⁴ kg).

If we have a particle of mass m on the surface of the earth, the gravitational force of attraction is given by:

W (its weight) = mg = GMm/R² ...(1)

From equation (1):

g = GM/R² ...(2)

Using the measured values:

• g ≈ 9.8 m/s²
• G = 6.672 × 10⁻¹¹ Nm²/kg²
• R ≈ 6371 km

M = gR²/G = 5.97 × 10²⁴ kg ...(3)

Historical Note: Cavendish's first measurement of G was referred to as "weighing the earth"

(A) Variation of g with Altitude

At an altitude h above the earth's surface:

R' = distance from the centre of the earth = R + h

g' = GM/(R+h)² = GM/R² × [R²/(R+h)²]

g' = g × [R/(R+h)]²

g' = g/(1 + h/R)² ...(4)

For h << R:

g' ≈ g(1 - 2h/R) ...(5)

Example: At a height of 10 km from the surface, the acceleration due to gravity decreases by a fraction of 2h/R = 2×10/6400 ≈ 0.31%

(B) Variation of g with Depth

At a depth x below the earth's surface, only that portion of the earth that is enclosed by a sphere of radius R_s (= R - x) centred at the earth's centre is effective.

[Earth cross-section showing effective radius R_s = R - x at depth x]

If we assume the earth to be a sphere having uniform density:

g' = GM'/R_s² = G(4/3)πR_s³ρ/R_s²

= (4/3)πGρR_s = (4/3)πGρ(R-x)

= g(R-x)/R

g' = g(1 - x/R) ...(6)

Example: At a depth of 10 km below the earth's surface, the fractional decrease in acceleration due to gravity is x/R = 10/6400 ≈ 0.16%

(C) Variation with Latitude

The effective value of the acceleration due to gravity changes with latitude owing to the rotation of the earth.

[Earth showing point Q at latitude θ with centrifugal force components]

At a latitude θ (Point Q), the effective weight:

mg' = mg - mω²r cosθ ...(1)

Where mω²r is the "centrifugal force" and we take its component in the vertical direction.

Now, r = radius of the circle of rotation of Q = QR = R cosθ

Therefore:

g' = g - ω²R cos²θ

g' = g - ω²R cos²θ ...(2)

Where:

ω = 2π/(24×3600) = 7.27 × 10⁻⁵ rad/s

So:

ω²R/g ≈ 0.34%, which is indeed a very small effect

Exercise 3:

1. (i) Neglecting air friction and technical difficulties, can a satellite be put into an orbit by being fired from huge cannon at the earth's surface?
2. (ii) Some body says "I weigh less than what I exactly weigh". Is he right? Is there any place on earth where he can weigh exactly?

ANSWERS TO EXERCISES

Exercise 2 Answers:

(i) The escape velocity is the same regardless of the angle of projection (45° or any other angle). The escape velocity depends only on the initial speed, not the direction.

(iii)

• (a) Total mechanical energy less than zero: The projectile will return to the earth's surface
• (b) Total mechanical energy greater than zero: The projectile will not return to the earth's surface

FORMULAE AND CONCEPTS AT A GLANCE

Key Formulae Summary:

1. Newton's Law of Gravitation:

F = Gm₁m₂/r²

2. Superposition Principle:

F⃗ = F₁ + F₂ + ... + F_n

where F₁, F₂, ... are the gravitational forces on a particle of mass m₀ due to particles of masses m₁, m₂, ... m_n respectively.

3. Force of Gravity:

F = mg, where m is mass of particle, g is acceleration due to gravity

4. Acceleration Due to Gravity:

g = GM/R² where M is the mass of earth and R is radius of earth

5. Variation of g with height:

(i) g_h = g/(1 + h/R)²

(ii) g_h = g(1 - 2h/R) for h << R

(iii) % change in g with height = (2h/R) × 100%

6. Variation of g with depth:

(i) g_d = g(1 - d/R)

(ii) % change in g with depth d = (d/R) × 100%

7. Variation of g with rotation of earth:

(i) g' = g - ω²R cos²λ

Where λ is the latitude of a place, ω is the angular velocity of rotation of earth.

At equator, λ = 0°, g' = g - ω²R

At pole, λ = 90°, g' = g

8. Gravitational intensity and gravitational potential:

i) Gravitational intensity at a point in a gravitational field = acceleration due to gravity at that point

ii) Gravitational potential at the point V = -GM/r

9. Gravitational Energy:

i) Gravitational potential energy = -GMm/r

ii) Total gravitational energy = gravitational PE + KE

10. Satellite:

i) Orbital velocity v₀ = √(GM/r) = √(gr)

ii) Time period of revolution of satellite, T = 2π√(r³/GM)

iii) Height of satellite, h = r - R

11. Escape velocity:

i) Escape velocity v_e = √(2GM/R) = √(2gR)

ii) Velocity outside the gravitational field is v = √(v₀² - 2GM/r)

12. Kepler's laws:

T² ∝ R³ where T is the time period of revolution of a planet and R is the orbital radius of the planet around sun.

GRAVITATION - SOLVED PROBLEMS

Problem 1: Period of Rotation for Weightlessness

Question: The period of rotation of earth so as to make any object weightless on its equator is

Options:

1. 84 min
2. 24 Hours
3. 84π min
4. π min

Where M and r are the mass and radius of earth.

Solution:

Put g_e = 0, in the expression:

g_e = g₀ - rω²

For weightlessness, g_e = 0:

0 = g₀ - rω²
⟹ ω = √(g₀/r)

Time period:

T = 2π/ω = 2π√(r/g₀)

Substituting r = 6.4 × 10⁶ m and g₀ = 9.8 m/s², we obtain:

T = 2π√(6.4 × 10⁶/9.8) = 84 min

Hence (A) is correct answer

Diagram: Earth rotating showing equatorial region with centrifugal force balancing gravitational force

Problem 2: Kinetic Energy of Satellite

Question: For a satellite if the time of revolution is T, then Kinetic energy is proportional to

Options:

1. 1/T
2. 1/T²
3. 1/T³
4. T^-2/3

Solution:

From Kepler's third law:

T² ∝ r³
⟹ r ∝ T^2/3

Orbital velocity:

v = √(GM/r) ∝ 1/√r ∝ 1/T^1/3

Kinetic Energy:

KE = ½mv² ∝ v² ∝ 1/T^2/3

Hence, KE ∝ T^-2/3

Hence (D) is correct answer

Problem 3: Gravitational Potential

Question: The gravitational field due to a mass distribution is given by I = (A/x³) in X-direction. The gravitational potential at a distance x is equal to

Options:

1. -A/(2x²)
2. -A/x²
3. -A/(3x²)
4. A/(2x²)

Solution:

The potential at a distance x is:

V(x) = -∫ I dx = -∫ (A/x³) dx

Integrating:

V(x) = -A ∫ x^-3 dx = -A × (x^-2/(-2)) + C
V(x) = A/(2x²) + C

Taking C = 0 (potential at infinity is zero):

V(x) = A/(2x²)

Hence (D) is correct answer

Problem 4: Potential Energy of Three Particles

Question: Three particles each of mass m are placed at the corners of an equilateral triangle of side d. The potential energy of the system is

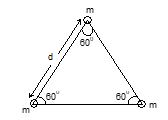
Options:

1. -Gm²/d
2. -2Gm²/d
3. -3Gm²/d
4. none of these

Solution:

For the system of two particles, gravitational potential energy is given as:

U = -Gm₁m₂/r

Total potential energy of the system:

U_total = U₁₂ + U₂₃ + U₃₁
U_total = -Gm²/d - Gm²/d - Gm²/d
U_total = -3Gm²/d

Note: The negative sign indicates that the particles are bound by their mutual gravitational field.

Hence (C) is correct answer

Diagram: Equilateral triangle with three masses m at vertices, each separated by distance d

Problem 5: Fractional Change in g with Height

Question: The fractional change in the value of free-fall acceleration 'g' for a particle when it is lifted from the surface to an elevation h (h<<R) is

Options:

1. 2h/R
2. -2h/R
3. h/R
4. none of these

Solution:

At surface: g = GM/R²

At height h: g' = GM/(R+h)²

g' = GM/(R+h)² = GM/R² × 1/(1+h/R)²
g' = g × (1+h/R)^-2

For h << R, using binomial expansion:

g' ≈ g(1 - 2h/R)

Fractional change:

Δg/g = (g' - g)/g = -2h/R

Hence (B) is correct answer

Problem 6: Work Done by Gravity on Satellite

Question: The work done by gravity of earth in maintaining a satellite in its orbit is

Options:

1. 0
2. >0
3. GMm/r²
4. -GMm/r

Where M, m are masses of earth and satellite and r = radius of the orbit.

Solution:

Since the earth-satellite system is moving in a circular orbit, the gravitational force of earth F⃗ and the displacement ds⃗ of the satellite are mutually perpendicular.

Work done by gravity = W = ∫ F⃗ · ds⃗
= ∫ |F||ds| cos 90°
= 0

Key Point: The gravitational force is always radial (towards center) while displacement is tangential, making them perpendicular.

Hence (A) is correct answer

Diagram: Satellite in circular orbit showing radial gravitational force and tangential velocity vectors

Problem 7: Energy Required to Remove Body from Earth

Question: The energy required to remove a body of mass m from earth's surface is/are equal to

Options:

1. GMm/R
2. mgR
3. -mgR
4. none of these

Solution:

Potential energy of the body on the surface of earth:

U₁ = -GMm/R

Potential energy of the body at infinity:

U₂ = 0

Energy required:

ΔU = U₂ - U₁ = 0 - (-GMm/R) = GMm/R

Since g = GM/R²:

ΔU = GMm/R = gRm = mgR

Hence (A) and (B) are correct answers

Problem 8: Tension in String with Two Masses

Question: Two particles of mass m each are connected by a very light string falling from a small height h. The tension in the string is (ℓ is the length of the string and ℓ<<R, h<<R, where R is radius of the earth)

Options:

1. Zero
2. mg/2
3. mg(ℓ/R)
4. non-zero

Solution:

We know that the acceleration due to gravity decreases with altitude. The particle m₂ that is nearer to earth accelerates more than the other particle m₁ that is farther from earth's surface.

The relative acceleration between the particles is not zero. Therefore, the string is stretched, consequently creating a tension in the string.

Key Points:

• When the length of the string is negligible, both m₁ and m₂ will have same acceleration because variation of acceleration due to gravity between them is negligible (zero).
• If ℓ << R, then the difference in weight = 2mg(ℓ/R) (numerically).

Tension in the string = mg(ℓ/R)

Hence (C) is correct answer

Diagram: Two masses connected by string at different heights showing differential gravitational effects

ASSIGNMENT

1. What is the value of acceleration at a height equal to the radius of earth?

Options: (A) g/2 (B) g/4 (C) 3g/4 (D) 0

2. Gravitational acceleration at the centre of earth is

Options: (A) Zero (B) g/2 (C) g (D) 3g/4

3. If a satellite be rotating about a planet which of the following is true. Where U = Potential energy of planet satellite system; K = kinetic energy of satellite; T = Total Mechanical energy

Options: (A) |U| = K = |T| (B) K = |T| = |2U| (C) 2K = |T| = |U| (D) K = |T| = |½U|

4. Escape velocity of a body on the earth's surface does not depend upon

Options: (A) Mass of earth (B) Radius of earth (C) Mass of body to escape (D) Universal gravitational constant

5. Newton's law of gravitation is given for two point masses m₁ and m₂ separated by a distance r.

Options: (A) The law can be applied as such for two large bodies provided r is the distance between their centers of mass. (B) The law cannot be used to find forces between extended bodies. (C) It is applicable to regular geometrical figures such as a cube only. (D) It is applicable to uniform spherical distribution of masses, r being the distance between their centers of mass

6. A planet revolves in an elliptical orbit around the sun, then out of following physical quantity the one, which remains constant, is

Options: (A) velocity (B) kinetic energy (C) momentum (D) angular momentum

7. A body of mass m is taken to the bottom of a deep mine. Then:

Options: (A) its mass increases (B) its mass decreases (C) its weight increases (D) its weight decreases

8. If the earth is at one fourth of its present distance from the sun, the duration of the year will be:

Options: (A) half the present year. (B) one-eighth the present year. (C) one-fourth the present year. (D) one-sixth the present year.

9. A satellite of the earth is revolving in a circular orbit with a uniform speed v. If the gravitational force suddenly disappears, the satellite will

Options: (A) continue to move with velocity v along the original orbit. (B) move with a velocity v, tangentially to the original orbit. (C) fall down with increasing velocity. (D) ultimately come to rest somewhere on the original orbit.

10. A satellite is moving round the earth with velocity v. To make the satellite escape, the minimum percentage increase in its velocity is nearly

Options: (A) 41.4% (B) 82.8% (C) 100% (D) None of these.

11. The gravitational potential energy of a rocket of mass 100kg at a distance 10⁹ m from the earth's surface is 4×10⁷J. The weight of the rocket in newtons at a distance 10⁹m from earth is (R_e = 6400km).

Options: (A) 8×10⁻²N (B) 8×10⁻³N (C) 4×10⁻³N (D) 4×10⁻²N

12. A body, which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth, then its velocity on reaching the surface of the earth is

Options: (A) √(gR) (B) √(gR/2) (C) √(2gR) (D) √(gR/4)

13. A missile is launched with a velocity less than the escape velocity. The sum of its kinetic and potential energy is

Options: (A) positive (B) negative (C) zero (D) may be positive or negative depending upon its initial velocity

14. The orbital speed of Jupiter is

Options: (A) greater than the orbital speed of earth. (B) less than the orbital speed of earth. (C) equal to the orbital speed of earth (D) zero.

15. Consider a satellite going round the earth in a circular orbit. Which of the following statement is wrong?

Options: (A) It is a freely falling body. (B) It is acted upon by a force directed away from the centre of the earth, which counter-balances the gravitational pull. (C) It is moving with a constant speed. (D) Its angular momentum remains constant.

ANSWERS TO ASSIGNMENT

1. B

2. A

3. D

4. C

5. D

6. D

7. D

8. B

9. B

10. A

11. D

12. B

13. B

14. A

15. B

Detailed Answer Explanations

1. (B) g/4: At height h = R, g' = g/(1+h/R)² = g/(1+1)² = g/4

2. (A) Zero: At the center of Earth, effective mass contributing to gravity is zero.

3. (D) K = |T| = |½U|: For circular orbits, K = GMm/2r, U = -GMm/r, T = K + U = -GMm/2r

4. (C) Mass of body to escape: v_e = √(2GM/R) is independent of the escaping body's mass.

5. (D): Newton's law applies to uniform spherical distributions treating them as point masses.

6. (D) Angular momentum: From Kepler's second law, angular momentum is conserved.

7. (D) Weight decreases: As we go deeper, effective gravitational field decreases.

8. (B) One-eighth: From Kepler's third law, T² ∝ r³, so T ∝ r^3/2. If r becomes r/4, T becomes T/8.

9. (B): By Newton's first law, it will continue with the same velocity tangentially.

10. (A) 41.4%: v_escape = √2 × v_orbital. Percentage increase = (√2 - 1) × 100% ≈ 41.4%

11. (D) 4×10⁻²N: From U = -GMm/r and F = GMm/r², we can find the weight.

12. (B) √(gR/2): Using energy conservation from height R to surface.

13. (B) Negative: Total energy is negative for bound systems (v < v_escape).

14. (A) Greater: This is incorrect - Jupiter's orbital speed is actually less than Earth's.

15. (B) Wrong statement: There's no outward force; only gravity provides centripetal acceleration.