Laws of Motion

Dynamics

It is the study of the cause of motion along with its description. This chapter, we are going to propose relationship between the force and the consequent motion of a body on which the force acts.

Force

Force is that external agent which:

1. Produces or tries to produce motion in a body at rest.
2. Stops or tries to stop a moving body.
3. Changes or tries to change the direction of motion of body.
4. Produces a change in the shape of the body.

Unit of Force: Its unit is Newton in SI system and dyne in CGS system.

Dimension: MLT^-2

Types of Forces

Based on the nature of the interaction between two bodies, forces may be broadly classified as under:

(a) Contact Forces

Tension, Normal Reaction, Friction, etc. Forces that act between the contact surfaces of the bodies is called contact force.

(b) Field Forces (Non-contact Forces)

Weight, electrostatic forces, etc. Forces that act between bodies separated by a distance without any actual contact is called Field Force.

Since we're going to encounter these forces in our analysis we will briefly discuss each force and how it acts between two bodies, its nature, etc, and how we are going to take it into account.

Contact Forces

i) Tension (T) - Attachment Force

When a string, thread, wire or a spring is held taut, the ends of the string or thread (or wire) pull on whatever bodies are attached to them in the direction of the string. This force is known as Tension.

If the string or spring is massless then the tension, T has the same magnitude at all points throughout the string.

The direction of tension is always away from the point of attachment to the body.

ii) Normal Contact Force

When two surfaces are in contact, then the surfaces exert the force on each other. The forces are opposite to each other in direction and equal to each other. The direction is always at right angle to the surfaces in contact i.e. at right angle to the common tangent to the surfaces at the point of contact.

iii) Parallel Contact Force (Friction)

It is a force that acts between bodies in contact with each other along the surface of contact – and it opposes relative motion between the two bodies. It is also called friction force.

If normal contact force (N) and parallel contact force (f) then contact force:

F = √(N² + f²)

Newton's First Law

Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change the state by an external force.

i.e. If vector sum of all the forces acting on a particle is zero then the particles remains at rest or move with constant velocity.

a = 0 if and only if ΣF = 0

or ΣFx = 0, ΣFy = 0, ΣFz = 0 It is condition of equilibrium.

Therefore, Newton's first law defines force. Force that external agent which causes a change in the state of a body.

Inertia

Inertia is the property of a body by virtue of which a body retains its state; either of rest or uniform motion along straight line. When a car suddenly starts moving the passengers in the car are thrown back due to inertia of rest. Similarly, when the car stops suddenly, the passengers stoop forward due to inertia (of motion).

The mass of a body can, therefore, be defined as the measure of its inertia.

Exercise 1:

(i) When a car suddenly takes a turn you are thrown off your seat. Why?

(ii) A fan fitted to a boat blows air at the sail of it. How will the boat accelerate.

Momentum

Momentum is the measure of motion contained in a body. The product of mass and velocity of the body measures it. Its direction is same as the velocity of the body.

P = mv

where:

• p = momentum of the body
• m = mass of the body
• v = velocity of the body

Unit: Its unit is kg-m/s in SI system and gm-cm/s in CGS system.

Dimension: Its dimension is MLT^-1

Newton's Second law of motion

Newton's second law states that the rate of change of momentum of a body is directly proportional to the impressed force and takes place in the direction of the applied force. The second law of motion relates two different physical quantities already known to us, viz. force and momentum.

The first law tells us that force (a push or a pull) causes a change in the velocity of a body, the second law now gives a quantitative description of this change.

If a body of mass m is moving with a velocity v, then its momentum is: p = mv  ... (1)

According to Newton's 2nd law, if a net force F acts on the body:

F = dp/dt    ... (2)

If the mass of the body, m is constant, then:

F = m(dv/dt) = ma      ... (3)

If the velocity of the body is constant, then:

F = v(dm/dt)    ... (4)

If mass and velocity of the body change with time then:

F = ma + v(dm/dt)    ... (5)

SI unit: Newton (N)

Dimensional formula: [MLT^-2]

Newton's Third Law of Motion

Every action has an equal and opposite reaction and action and reaction acting on the two different bodies.

Consider two bodies A and B interacting with each other, by means of forces:

• F_AB: the force exerted by body B on A
• F_BA: The force exerted by the body A on B

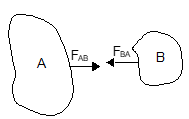
According to Newton's 3rd law: F_AB = -F_BA (equal in magnitude & opposite in direction)

Exercise 2:

i) Newton's Second law measures force while Newton's first law defines it. Is it true?

ii) You are marooned on a plane made of ice. How can you get out of the plane? Will you roll? Will you jump? Or will you spit and sneeze?

iii) In a tug of war if both the parties apply equal and opposite force on the rope, then how can one party win?

Application of Newton's Law of Motion

Newton's laws can be applied to study the motion of a body under the influence of a force or a set of forces. To make the study simpler we take the model of the body and represent it by a point. i.e. the body itself is considered a point mass. The diagram showing all external forces acting on an object is called free body diagram. After representing the forces the following methods may be adopted to study the motion of the body:

1. Firstly consider the origin of the forces acting on each object. To do this find out the field forces acting on the object. Wherever contact is available account the contact forces carefully.
2. Secondly draw the forces in the given problem, decide whether the system at all can accelerate or not.
3. If it accelerates, find its direction.
4. Isolate the system and draw the forces acting on the system. Here replace the actual system by a point mass. This is the free body diagram (F.B.D.). Show the direction of acceleration with an arrow.
5. In case of a composite problem of a number of bodies connected by strings and pulleys – find the relationship of accelerations of different bodies by constraint relationship [discussed later].
6. With reference to direction of motion of the system, select suitable co-ordinate axes according to convenience i.e. there is no necessity to use the same co-ordinate axes for all the bodies.
7. Resolve all external forces along the chosen axes. Set up equation of motion along the individual axis as (ΣF_ext)_x = Ma_x and (ΣF_ext)_y = Ma_y. Finally get the net acceleration as, a = a_x + a_y i.e. a = √(a_x² + a_y²) with direction as w.r.t. x-axis θ = tan^-1(a_y/a_x).

Spring Force

According to Hooke's Law the extension or compression produced in a spring is directly proportional to the force applied on it. If x is the deformation in the spring then:

F ∝ x

or F = -kx

Where k is constant and is called spring constant or force constant. The negative sign shows that the force and the extension or compression are opposite in their directions.

The direction of force either due to compression or extension is directed against the direction of compression or extension.

Frictional Force

Frictional force comes into play between two surfaces whenever there is relative motion or tendency of relative motion between the surfaces. Frictional force has tendency to destroy the relative motion of the surfaces.

Friction is a self-adjusting force. It changes its direction and magnitude according to the applied force or the force, which causes a tendency in the body to move.

Types of Friction

(a) Static Friction

Which acts between surfaces in contact but not in relative motion, it opposes the tendency of relative motion.

(b) Kinetic Friction

Which acts between surfaces in contact which are in relative motion, it opposes the relative motion between the surfaces.

Kinetic friction can be further classified as:

• Sliding friction
• Rolling friction

Laws of Static Friction

Static Friction, acting between surfaces in contact, but not in relative motion, opposes the tendency of relative motion between the surfaces.

The maximum value of static friction:

f_s(max) = μ_sN

Where μ_s = coefficient of static friction

N = normal reaction of the block from the surface

0 ≤ f_s ≤ μ_sN

Kinetic friction:

f_k = μ_kN

Where μ_k = coefficient of kinetic friction

Note:

• If external force is less than limiting friction force then friction force = external force
• If external force greater than limiting frictional force then friction force = kinetic friction force

Angle of Friction

The angle between the normal reaction and the resultant of normal reaction and frictional force is called angle of friction.

tan θ = f/N

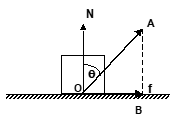
Angle of Repose

Consider a body of mass m resting on an inclined plane of inclination θ. The forces acting on the body are shown in the figure—F_f being the force of friction. If friction is large enough, the body will not slide down.

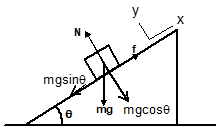
Choosing coordinates as shown, for equilibrium:

• Along x-axis: ΣF_x = 0  →  mg sinθ − F_f = 0
• Along y-axis: ΣF_y = 0  →  N − mg cosθ = 0

∴   N = mg cosθ  and  F_f = mg sinθ.

Since   F_f ≤ μ_sN,   we get
mg sinθ ≤ μ_s mg cosθ.

⇒   tanθ ≤ μ_s.

Thus, for the body not to slide down, the angle must satisfy tanθ ≤ μ_s, where μ_s is the coefficient of static friction between the two surfaces. When θ is increased so that tanθ > μ_s,
sliding begins.

The angle at which sliding starts, θ_r, is called the angle of repose and satisfies
tanθ_r = μ_s (i.e., θ_r = tan⁻¹μ_s).

Frame of Reference

It is a conveniently chosen co-ordinate system, which describes the position and motion of a body in the space.

Internal Frame of Reference

A co-ordinate system whose origin is either at rest or in uniform motion along a straight line. Newton's laws are strictly valid only for inertial frame.

Non - Internal Frame of Reference

A co-ordinate system whose origin is accelerating is called a non-inertial frame of reference.

Pseudo Force

When the motion of a body in a non-inertial frame of reference is considered then a force which is non-existent in inertial frame comes into play. This force is called Pseudo Force. The magnitude of this force is the product of the mass of the body and the acceleration of the frame.

The direction of the Pseudo force is in opposite direction to the acceleration of the frame of reference.

Centripertal Force & Centrifugal Force

If a body is moving with a constant speed in a circle, as seen from an inertial frame it is continuously accelerated towards the centre of rotation. The magnitude of the centripetal acceleration for a tangential velocity v is given by v²/r. If the angular velocity of the body is ω then the centripetal acceleration is rω².

As per Newton's law to cause an acceleration a force is required which is equal to ma = mv²/r or centripetal force is:

F = mv²/r = mω²r

Centripetal force is not a new kind of force. Whenever the direction of force is towards the centre it provides the necessary centripetal force.

When the body is observed from non-inertial frame i.e. the rotating frame itself then the body will be under a pseudo force which is called the centrifugal force.

As the direction of Pseudo force is opposite to the direction of the acceleration of the frame, Centrifugal force should be opposite to the direction of centripetal acceleration i.e. away from the centre. Its magnitude should be product of the mass of the body and centripetal acceleration.

Numerically it is equal to the centripetal force but is oppositely directed. Remember it is fictitious and has non-existent if considered from internal frame.

Exercise 3:

i) What causes the motion of a car on a road?

ii) Tell the direction friction that acts on the front wheel and rear wheel of a cycle.

iii) If the centripetal and centrifugal forces are equal in magnitude and opposite in direction does the body remain under equilibrium due to these two forces?

Formulae & Concepts at a glance

1. For equilibrium: ΣF = 0, i.e. ΣF_x = 0, ΣF_y = 0, ΣF_z = 0
2. Momentum: P = mv
3. Force: F = dp/dt = d/dt(mv) = v(dm/dt) + m(dv/dt)
   • If velocity is constant and mass varies with time then F = v(dm/dt)
   • If m is constant and velocity varies with time then F = m(dv/dt) = ma
4. Impulse: J = Δp = change in momentum = m(v - u)
   • J = ∫Fdt (when force is variable)
   • J = F·t (when force is constant)
5. Thrust on the rocket: F = -u(dm/dt)
   • Where u = exhaust speed of the burnt gases
   • dm/dt = rate of burning of fuel
   • Acceleration of rocket at any instant: a = (upthrust - weight)/mass
6. Apparent weight of mass in lift:
   • R = m(g+a), where a is upward acceleration of the lift
   • R = m(g-a), where a is downward acceleration of the lift
   • In free fall under the action of gravity a = g, R = 0 (weightless)
   • When lift is at rest or moving uniformly a = 0, R = mg
7. If α is angle of repose and μ is coefficient of friction then tan α = μ
8. If N = normal contact, f = parallel contact force, then contact force F = √(N² + f²)
9. Centripetal force: F_c = mv²/r = mω²r
10. If a_t = tangential acceleration and a_r = radial acceleration of the body moving in circular path, then total acceleration a = √(a_t² + a_r²)

11. Motion of a block on a horizontal smooth surface

Different Cases	Results
(a) When subjected to a horizontal pull	(i) R = mg (ii) a = F/m
(b) When subjected to a pull acting at an angle to the horizontal	(i) R = mg - Fsinθ (ii) a = Fcosθ/m
(c) When subjected to a push acting at an angle θ to the horizontal	(i) R = mg + Fsinθ (ii) a = Fcosθ/m

12. Motion of a block on a smooth inclined plane

Different Cases	Results
(a) When smooth inclined plane is fixed	(i) R = mgcosθ (ii) a = gsinθ
(b) When the smooth inclined plane is moving horizontally with an acceleration b	(i) R = m(gcosθ + bsinθ) (ii) a = (gsinθ - bcosθ)

13. Motion of bodies in contact: Force of contact

Different Cases	Results
(a) When two bodies are kept in contact and force is applied on the body of mass m₁	(i) a = F/(m₁ + m₂) (ii) f = m₂F/(m₁ + m₂)
(b) When two bodies are kept in contact and force is applied on the body of mass m₂	(i) a = F/(m₁ + m₂) (ii) f = m₁F/(m₁ + m₂)
(c) When three bodies are kept in contact and force is applied on the body of mass m₁	(i) a = F/(m₁ + m₂ + m₃) (ii) T₁ = (m₂ + m₃)F/(m₁ + m₂ + m₃) (iii) T₂ = m₃F/(m₁ + m₂ + m₃)

14. Motion of connected bodies

Different Cases	Results
(a) When two bodies are connected through strings and placed on a smooth horizontal surface	(i) a = F/(m₁ + m₂) (ii) T = m₁F/(m₁ + m₂)
(b) When three bodies are connected through strings on a smooth horizontal surface	(i) a = F/(m₁ + m₂ + m₃) (ii) T₁ = m₁F/(m₁ + m₂ + m₃) (iii) T₂ = (m₁ + m₂)F/(m₁ + m₂ + m₃)
(c) When two bodies are attached at the ends of a string passing over a pulley	(i) a = (m₁ - m₂)g/(m₁ + m₂) (ii) T = 2m₁m₂g/(m₁ + m₂)
(d) When mass m₁ rests on a smooth horizontal table and mass m₂ is hanging vertically	(i) a = m₂g/(m₁ + m₂) (ii) T = m₁m₂g/(m₁ + m₂)
(e) When mass m₁ is placed on a smooth inclined plane making an angle θ with horizontal	(i) a = (m₂ - m₁sinθ)g/(m₁ + m₂) (ii) T = m₁m₂g(1 + sinθ)/(m₁ + m₂) (iii) If system remains in equilibrium: m₁gsinθ = m₂g

15. Comparison between downward motion on smooth and rough inclined planes

S.No.	Physical quantity	Smooth inclined plane	Rough inclined plane	Conclusion
1.	Acceleration	aS = gsinθ	aR = gsinθ - μgcosθ	aR < aS
2.	Time of descent	tS = √(2L/gsinθ)	tR = √(2L/(gsinθ - μgcosθ))	tR > tS
3.	Velocity at bottom	vS = √(2gLsinθ)	vR = √(2gL(sinθ - μcosθ))	vR < vS

16. Comparison of downward and upward motions on a rough inclined plane

S.No.	Physical quantity	Downward motion	Upward motion	Conclusion
1.	Acceleration	aD = g(sinθ - μcosθ)	AU = -g(sinθ + μcosθ)	aU > AD
2.	Time of travel	tD = √(2L/g(sinθ - μcosθ))	tU = √(2L/g(sinθ + μcosθ))	tU < tD
3.	Work done by the driving force	WD = FL = mg(sinθ - μcosθ)L	WU = FL = mg(sinθ + μcosθ)L	WU > WD
4.	Force required to drag with an acceleration a	FD = mg(μcosθ - sinθ) + ma	FU = mg(μcosθ + sinθ) + ma	FU > FD

17. Motion of connected bodies on rough surfaces

S.No.	Different types of system	Results
1	Two masses connected by string over pulley, one on rough horizontal surface	(i) a = (m₂g - μm₁g)/(m₁ + m₂) (ii) T = m₁m₂g(1 + μ)/(m₁ + m₂)
2	One mass on rough inclined plane, other hanging vertically	(i) a = unbalanced force/total mass = (m₂g - m₁gsinθ - μm₁gcosθ)/(m₁ + m₂) (ii) T = m₁m₂g(1 + sinθ + μcosθ)/(m₁ + m₂)
3	Both masses on inclined planes at different angles	(i) a = [m₂g(sinθ₂ - μ₂cosθ₂) - m₁g(sinθ₁ + μ₁cosθ₁)]/(m₁ + m₂) (ii) Calculate tension using Newton's 2nd law equations
4	Both masses on same inclined plane	(i) a = [m₁gsinθ + m₂gsinθ - gcosθ(μ₁m₁ + μ₂m₂)]/(m₁ + m₂) (ii) Apply Newton's 2nd law to find tensions

Solved Problems

Problem 1: A reference frame attached to earth is

(A) an inertial frame sometimes

(B) an inertial is frame always

(C) a non-inertial frame

(D) may be inertial or non-inertial.

Solution: As the earth itself is rotating about on its axis the frame attached to it should be a non-inertial one.

Hence C is correct answer

Problem 2: A vehicle is moving on a rough road in a straight line with uniform velocity.

(A) No force is acting on vehicle

(B) A force must act on the vehicle

(C) An acceleration is being produced in the vehicle

(D) No work is being done on the vehicle.

Solution: As the vehicle is moving with a uniform velocity it is under equilibrium. Net force acting on it should be zero.

Hence A is correct answer

Problem 3: Two identical particles A and B, each of mass m, are interconnected by spring of stiffness k. If the particle B experiences a force F & the elongation of the relative spring is x, the relative acceleration between the particles is equal to

(A) F/2m

(B) (F - kx)/m

(C) (F - 2kx)/m

(D) kx/m

class="img-responsive"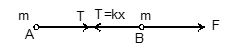

Solution: Equation of motion for A: T = ma ⇒ a = kx/m

For B: F - T = ma ⇒ a = (F - kx)/m

The relative acceleration = a_r = |a - a| = (F - 2kx)/m

Hence C is correct answer

Problem 4: A 60 kg man stands on a spring scale in a lift. At same instant he finds that the scale reading has changed from 60kg to 50 kg for a while and then comes back to the original mark. What should he conclude.

(A) The lift was in constant motion upwards

(B) The lift was in constant motion downwards

(C) The lift while in motion downward suddenly stopped

(D) The lift while in motion upward suddenly stopped.

Solution: When lift accelerates up W' = W(1 + a/g)

When lift decelerates up W' = W(1 - a/g)

Here weight decreases i.e. lift decelerates. Initially lift was moving with constant velocity up and then it suddenly stopped i.e. decelerated

Hence D is correct answer

Problem 5: A body is accelerated by applying a force of 30N. The change in momentum of the body after 2sec is

(A) 7.5 kg-m/s

(B) 30 kg-m/s

(C) 120 kg-m/s

(D) 60 kg-m/s

Solution: ΔP = F×t = 30×2 = 60 kg m/s

Hence D is correct answer

Problem 6: Two masses 2kg and 5kg are connected by a light string passing over a frictionless pulley. The tension in the cord connecting the masses will be

(A) 20N

(B) 30N

(C) 28 N

(D) 50 N

Solution: T = (2m₁m₂g)/(m₁ + m₂) = (2×5×2×9.8)/(5 + 2) = 28N

Hence C is correct answer

Problem 7: A vessel containing water is given a constant acceleration towards the right, along a straight horizontal path. Which of the following figures represents the surface of the liquid?

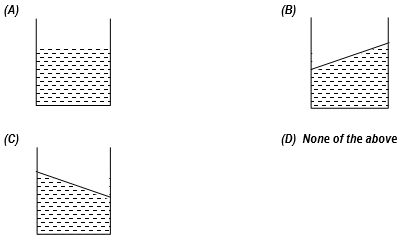
Solution: When vessel accelerates upward, the fictitious force acts on water, hence water is dragged backward.

Hence C is correct answer

Problem 8: A bob hanging from the ceiling of the car acts as an accelerometer. Then the relation expressing horizontal acceleration a of the car and the angle θ made by bob with the vertical is

(A) a = gtanθ

(B) a = gsinθ

(C) a = gcotθ

(D) None

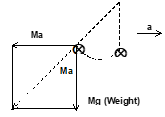
Solution: tanθ = Ma/Mg ⇒ a = gtanθ

Hence A is correct answer

Problem 9: A weight W is attached to two weightless strings AB and AC as shown in figure. The tension in each string will be

(A) W/4

(B) W/2

(C) (√3)W/2

(D) W

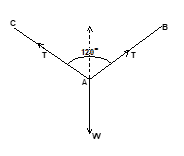
Solution: For vertical equilibrium: 2T cos60° = W

T = W/(2cos60°) = W

Hence D is correct answer

Problem 10: A body of mass 2kg is acted upon by two forces each of magnitude 1N, making an angle 60° with each other. The net acceleration of the body in m/s² is

(A) 0.1

(B) 1.0

(C) √3/2

(D) 2/√3

Solution: Net force F = √(F₁² + F₂² + 2F₁F₂cos60°)

= √(1² + 1² + 2×1×1×1/2) = √3N

a = F/M = √3/2 m/s²

Hence C is correct answer

Assignment

Q1. Two equal masses are kept on the pans of a simple balance in a lift accelerating upward then

(A) Pans will remain at the same level

(B) Nothing can be said as data is in complete

(C) Left side pan will lower down

(D) Right side pan will lower down

Q2. You are marooned on a frictionless horizontal due to place and can not exert any horizontal force by pushing against the surface. How can you get off?

(A) by jumping

(B) by rolling your body on the surface

(C) by splitting or sneezing

(D) By running on the plane

Q3. A man in a lift will weight more when:

(A) Lift accelerates upward

(B) Lift accelerates downward

(C) Lift descends freely

(D) The lift going up is slowing down

Q4. A man weighing mg in moving upward in a rocket with acceleration 4g. His apparent weight inside the rocket is

(A) Zero

(B) 4 mg

(C) 5mg

(D) mg

Q5. A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the string is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.

(A) mF/(m + M)

(B) MF/(m + M)

(C) mF/M

(D) (M + m)F/m

Q6. A force of 500N is required to push a car of mass 1000kg slowly at constant speed on a level road. If a force of 1000N is applied the acceleration of the car will be.

(A) 0

(B) 0.5 m/s²

(C) 10 m/s²

(D) 1.5 m/s²

Q7. A vessel containing water is given a constant acceleration a towards the right along a straight horizontal path. The resultant force acts:

(A) along OA

(B) along OB

(C) along OC

(D) along OD

Q8. A light bird on a stretched telegraph wire. The additional tension produced in the wire is

(A) zero

(B) Less then the weight of the bird

(C) Equal to the weight of the bird

(D) greater than the weight of the bird

Q9. A body of mass 50kg is pulled by a rope of length 6m on a frictionless surface by a force of 106N applied to the other end. The linear density of the rope is 0.5kg/m. The force acting on 50kg mass is

(A) 50N

(B) 100 N

(C) 150 N

(D) 200N

Q10. The mean force necessary to stop a hammer having momentum 25N in 0.05s must be

(A) 25N

(B) 50N

(C) 125N

(D) 500N

Q11. A fireman weighing 80 kg slides down a vertical pole. If the resisting force of friction is a constant value of 720 N, his acceleration in m/s² is (g = 10 m/s²)

(A) 0.01

(B) 1

(C) 0.1

(D) 0.03

Q12. A stretching force of 10 N is applied at one end of a spring balance and an equal force is applied at the other end at the same time. What will be the reading of the balance?

(A) 5 N

(B) 10 N

(C) 20 N

(D) 0

13. A person sitting in an open car at constant velocity throws a ball vertically up into the air. The ball falls

(A) In the car behind the person

B) In the car ahead of the person

(C) Outside the car

(D) Exactly in the hand which threw it up

Q14. A boy of 50 kg in standing in a lift moving down with an acceleration of 9.8 m/s². The apparent weight of the boy is

(A) 50 × 9.8

(B) 50 N

(C) Zero

(D) 50/9.8 N

Q15. A block m rests on a horizontal surface. The coefficient of static friction between the mass and the surface is μ. If the mass is pushed by a force F at 30° angle. The block is at rest. The friction acts on the block is

(A) μmg

(B) μ[mg - √3/2F]

(C) F cos30°

(D) μ[mg + (F/2)]

Answers to Assignment

1. A	2. C	3. A	4. C	5. A
6. B	7. C	8. D	9. B	10. D
11. B	12. B	13. D	14. C	15. C