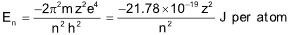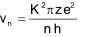The development of atomic models over time has shaped our current understanding of atomic structure. Each model was proposed based on experimental observations and helped address the shortcomings of previous theories. Here are five significant atomic models: Dalton’s Model (1803): Proposed that atoms are indivisible, solid spheres. While groundbreaking, this model couldn't explain atomic reactions or the presence of subatomic particles. Thomson’s Model (1897): Known as the "plum pudding model," it described the atom as a positively charged sphere embedded with negatively charged electrons, like raisins in a pudding. This model introduced electrons but lacked a structured nucleus. Rutherford’s Model (1911): Through the gold foil experiment, Rutherford concluded that atoms have a small, dense, positively charged nucleus with electrons orbiting around it. This model introduced the nuclear concept but couldn’t explain electron stability. Bohr’s Model (1913): Niels Bohr added that electrons move in fixed energy levels or orbits and could jump between levels by absorbing or emitting energy. This model worked well for hydrogen but failed for more complex atoms. Quantum Mechanical Model (1926): Based on Schrödinger’s wave equation, this model describes electrons as existing in probability clouds called orbitals. It incorporates the Heisenberg uncertainty principle and accurately predicts chemical behavior. Each model contributed crucial insights, with the quantum mechanical model currently accepted as the most accurate representation of atomic structure.

The development of atomic models over time has shaped our current understanding of atomic structure. Each model was proposed based on experimental observations and helped address the shortcomings of previous theories. Here are five significant atomic models: Dalton’s Model (1803): Proposed that atoms are indivisible, solid spheres. While groundbreaking, this model couldn't explain atomic reactions or the presence of subatomic particles. Thomson’s Model (1897): Known as the "plum pudding model," it described the atom as a positively charged sphere embedded with negatively charged electrons, like raisins in a pudding. This model introduced electrons but lacked a structured nucleus. Rutherford’s Model (1911): Through the gold foil experiment, Rutherford concluded that atoms have a small, dense, positively charged nucleus with electrons orbiting around it. This model introduced the nuclear concept but couldn’t explain electron stability. Bohr’s Model (1913): Niels Bohr added that electrons move in fixed energy levels or orbits and could jump between levels by absorbing or emitting energy. This model worked well for hydrogen but failed for more complex atoms. Quantum Mechanical Model (1926): Based on Schrödinger’s wave equation, this model describes electrons as existing in probability clouds called orbitals. It incorporates the Heisenberg uncertainty principle and accurately predicts chemical behavior. Each model contributed crucial insights, with the quantum mechanical model currently accepted as the most accurate representation of atomic structure.

Solving problems related to atomic structure involves applying concepts such as electron configuration, quantum numbers, isotopes, and periodic trends. Here’s a step-by-step guide: Identify Atomic Number (Z): This tells you the number of protons and, in a neutral atom, the number of electrons. Calculate Neutrons: Use the mass number (A) to subtract the atomic number (Z), i.e., Neutrons = A – Z. Write Electron Configuration: Distribute electrons into orbitals based on the Aufbau principle, e.g., Oxygen (Z=8) → 1s² 2s² 2p⁴. Assign Quantum Numbers: For any given electron, determine the four quantum numbers (n, l, m, s) that describe its energy level, subshell, orbital, and spin. Apply Periodic Trends: Use atomic structure to predict trends such as electronegativity, atomic radius, and ionization energy. For example, atoms with more protons have smaller radii due to greater nuclear attraction. Interpret Isotopes and Ions: For ions, add or subtract electrons. For isotopes, identify the same number of protons but different numbers of neutrons. Practicing MCQs and numerical problems—like finding the number of electrons in ions or determining atomic radii differences—can strengthen your skills. Use visual tools like orbital diagrams and electron cloud sketches to aid conceptual understanding.

Solving problems related to atomic structure involves applying concepts such as electron configuration, quantum numbers, isotopes, and periodic trends. Here’s a step-by-step guide: Identify Atomic Number (Z): This tells you the number of protons and, in a neutral atom, the number of electrons. Calculate Neutrons: Use the mass number (A) to subtract the atomic number (Z), i.e., Neutrons = A – Z. Write Electron Configuration: Distribute electrons into orbitals based on the Aufbau principle, e.g., Oxygen (Z=8) → 1s² 2s² 2p⁴. Assign Quantum Numbers: For any given electron, determine the four quantum numbers (n, l, m, s) that describe its energy level, subshell, orbital, and spin. Apply Periodic Trends: Use atomic structure to predict trends such as electronegativity, atomic radius, and ionization energy. For example, atoms with more protons have smaller radii due to greater nuclear attraction. Interpret Isotopes and Ions: For ions, add or subtract electrons. For isotopes, identify the same number of protons but different numbers of neutrons. Practicing MCQs and numerical problems—like finding the number of electrons in ions or determining atomic radii differences—can strengthen your skills. Use visual tools like orbital diagrams and electron cloud sketches to aid conceptual understanding.

A basic atom is the simplest representation of matter, composed of three main subatomic particles: protons, neutrons, and electrons. The protons (positive charge) and neutrons (neutral) reside in the atom’s nucleus, which is extremely small yet dense and carries most of the atom’s mass. Electrons (negative charge) revolve around the nucleus in defined energy levels or shells.The identity of an atom is determined by its number of protons, also known as its atomic number. For example, an atom with 6 protons is always a carbon atom. Neutrons add mass and help stabilize the nucleus, while electrons determine how the atom interacts chemically.Basic atoms are electrically neutral, meaning the number of protons equals the number of electrons. However, atoms can gain or lose electrons to form ions. Understanding the structure of a basic atom helps explain chemical bonding, molecular formation, and reactions.In educational terms, drawing a basic atom usually involves sketching a central nucleus with labeled protons and neutrons, and surrounding circular orbits or shells containing electrons. This foundational concept is essential for progressing in subjects like chemistry, biology, and physics, and for understanding the material world at the microscopic level.

A basic atom is the simplest representation of matter, composed of three main subatomic particles: protons, neutrons, and electrons. The protons (positive charge) and neutrons (neutral) reside in the atom’s nucleus, which is extremely small yet dense and carries most of the atom’s mass. Electrons (negative charge) revolve around the nucleus in defined energy levels or shells.The identity of an atom is determined by its number of protons, also known as its atomic number. For example, an atom with 6 protons is always a carbon atom. Neutrons add mass and help stabilize the nucleus, while electrons determine how the atom interacts chemically.Basic atoms are electrically neutral, meaning the number of protons equals the number of electrons. However, atoms can gain or lose electrons to form ions. Understanding the structure of a basic atom helps explain chemical bonding, molecular formation, and reactions.In educational terms, drawing a basic atom usually involves sketching a central nucleus with labeled protons and neutrons, and surrounding circular orbits or shells containing electrons. This foundational concept is essential for progressing in subjects like chemistry, biology, and physics, and for understanding the material world at the microscopic level.

Atomic structure refers to the composition and arrangement of subatomic particles within an atom. Every atom consists of a central nucleus, which contains positively charged protons and neutral neutrons, surrounded by a cloud of negatively charged electrons. These electrons orbit the nucleus in regions called energy levels or shells. The number of protons in the nucleus determines the atomic number of an element and defines its identity in the periodic table. Neutrons add to the mass but do not influence the charge.Electrons are arranged in shells based on energy levels, and the arrangement is governed by principles such as the Aufbau principle, Hund's Rule, and the Pauli exclusion principle. The outermost electrons, known as valence electrons, play a crucial role in chemical bonding and reactivity. Understanding atomic structure is foundational to chemistry, as it explains why elements behave the way they do, how they bond, and how reactions occur. From a practical standpoint, atomic structure also underpins modern technology, including electronics, energy production, and materials science.

Atomic structure refers to the composition and arrangement of subatomic particles within an atom. Every atom consists of a central nucleus, which contains positively charged protons and neutral neutrons, surrounded by a cloud of negatively charged electrons. These electrons orbit the nucleus in regions called energy levels or shells. The number of protons in the nucleus determines the atomic number of an element and defines its identity in the periodic table. Neutrons add to the mass but do not influence the charge.Electrons are arranged in shells based on energy levels, and the arrangement is governed by principles such as the Aufbau principle, Hund's Rule, and the Pauli exclusion principle. The outermost electrons, known as valence electrons, play a crucial role in chemical bonding and reactivity. Understanding atomic structure is foundational to chemistry, as it explains why elements behave the way they do, how they bond, and how reactions occur. From a practical standpoint, atomic structure also underpins modern technology, including electronics, energy production, and materials science.

Teaching atomic structure effectively requires a multi-sensory and scaffolded approach that builds on students' prior knowledge. Start by introducing the historical development of atomic theory, from Dalton to Bohr and beyond, to help students appreciate how the model has evolved. Use visuals like Bohr diagrams and 3D models to illustrate protons, neutrons, and electrons and how they are arranged in atoms. Incorporate interactive simulations and virtual labs to demonstrate how electrons occupy energy levels and how electron transitions relate to absorption or emission spectra.Analogies also help make abstract concepts concrete. For instance, comparing the atom to a solar system, with the nucleus as the sun and electrons as planets, can aid understanding. However, it's essential to explain the limitations of such analogies. Encourage active learning by asking students to draw atomic structures, identify isotopes, and calculate subatomic particles from atomic numbers and mass numbers. Reinforce concepts through quizzes, group discussions, and real-life examples, such as how atomic structure explains periodic trends or the behavior of elements in reactions. Incorporating current applications, like nuclear energy or medical imaging, adds relevance and fosters engagement.

Teaching atomic structure effectively requires a multi-sensory and scaffolded approach that builds on students' prior knowledge. Start by introducing the historical development of atomic theory, from Dalton to Bohr and beyond, to help students appreciate how the model has evolved. Use visuals like Bohr diagrams and 3D models to illustrate protons, neutrons, and electrons and how they are arranged in atoms. Incorporate interactive simulations and virtual labs to demonstrate how electrons occupy energy levels and how electron transitions relate to absorption or emission spectra.Analogies also help make abstract concepts concrete. For instance, comparing the atom to a solar system, with the nucleus as the sun and electrons as planets, can aid understanding. However, it's essential to explain the limitations of such analogies. Encourage active learning by asking students to draw atomic structures, identify isotopes, and calculate subatomic particles from atomic numbers and mass numbers. Reinforce concepts through quizzes, group discussions, and real-life examples, such as how atomic structure explains periodic trends or the behavior of elements in reactions. Incorporating current applications, like nuclear energy or medical imaging, adds relevance and fosters engagement.

The atomic structure theory explains how atoms are formed and how subatomic particles are arranged and interact. This theory has evolved over centuries, beginning with the idea of indivisible atoms proposed by Democritus and advancing through models by Dalton, Thomson, Rutherford, Bohr, and Schrödinger. Each model improved upon the previous by incorporating new experimental evidence and deeper understanding of quantum mechanics.Modern atomic theory posits that an atom consists of a dense nucleus containing protons and neutrons, with electrons existing in orbitals rather than fixed paths. These orbitals are regions of space around the nucleus where the probability of finding an electron is highest. The quantum mechanical model incorporates principles such as Heisenberg's uncertainty principle and Schrödinger's wave equation to explain the behavior of electrons.This theory helps explain periodic properties such as ionization energy, atomic radius, and electronegativity, all of which depend on electron configurations and nuclear charge. Understanding atomic structure theory is essential in disciplines ranging from chemistry and physics to biology and engineering, as it forms the basis for explaining matter's behavior at the microscopic level.

The atomic structure theory explains how atoms are formed and how subatomic particles are arranged and interact. This theory has evolved over centuries, beginning with the idea of indivisible atoms proposed by Democritus and advancing through models by Dalton, Thomson, Rutherford, Bohr, and Schrödinger. Each model improved upon the previous by incorporating new experimental evidence and deeper understanding of quantum mechanics.Modern atomic theory posits that an atom consists of a dense nucleus containing protons and neutrons, with electrons existing in orbitals rather than fixed paths. These orbitals are regions of space around the nucleus where the probability of finding an electron is highest. The quantum mechanical model incorporates principles such as Heisenberg's uncertainty principle and Schrödinger's wave equation to explain the behavior of electrons.This theory helps explain periodic properties such as ionization energy, atomic radius, and electronegativity, all of which depend on electron configurations and nuclear charge. Understanding atomic structure theory is essential in disciplines ranging from chemistry and physics to biology and engineering, as it forms the basis for explaining matter's behavior at the microscopic level.

Identifying an atom’s structure involves determining the number and arrangement of its subatomic particles: protons, neutrons, and electrons. This begins with the atomic number (Z), which tells you the number of protons. Since atoms are electrically neutral, the number of electrons is also equal to the atomic number. To determine the number of neutrons, subtract the atomic number from the atomic mass number (rounded to the nearest whole number).Once these values are known, you can represent the atomic structure using notations such as: Element symbol (e.g., C for carbon) Atomic number and mass number (e.g., 6C¹²) Electron configuration (e.g., 1s² 2s² 2p² for carbon) To visualize this, Bohr diagrams or Lewis dot structures are used. Bohr diagrams show electrons in specific energy levels, while Lewis structures highlight valence electrons. Advanced learners can use orbital diagrams and quantum numbers for more precise models.Scientific tools such as mass spectrometers, electron microscopes, and spectroscopy can also help identify atomic structure experimentally. In educational settings, students use periodic table data to predict and sketch atomic models. Mastering this skill enhances understanding of reactivity, isotopes, ion formation, and periodic trends.

Identifying an atom’s structure involves determining the number and arrangement of its subatomic particles: protons, neutrons, and electrons. This begins with the atomic number (Z), which tells you the number of protons. Since atoms are electrically neutral, the number of electrons is also equal to the atomic number. To determine the number of neutrons, subtract the atomic number from the atomic mass number (rounded to the nearest whole number).Once these values are known, you can represent the atomic structure using notations such as: Element symbol (e.g., C for carbon) Atomic number and mass number (e.g., 6C¹²) Electron configuration (e.g., 1s² 2s² 2p² for carbon) To visualize this, Bohr diagrams or Lewis dot structures are used. Bohr diagrams show electrons in specific energy levels, while Lewis structures highlight valence electrons. Advanced learners can use orbital diagrams and quantum numbers for more precise models.Scientific tools such as mass spectrometers, electron microscopes, and spectroscopy can also help identify atomic structure experimentally. In educational settings, students use periodic table data to predict and sketch atomic models. Mastering this skill enhances understanding of reactivity, isotopes, ion formation, and periodic trends.

The principles of atomic structure govern how subatomic particles are arranged and behave within an atom. Three foundational principles guide the electron configuration of atoms: Aufbau Principle – This states that electrons occupy the lowest energy orbitals first before filling higher ones. It explains why the 1s orbital fills before 2s or 2p orbitals. Pauli Exclusion Principle – This rule states that no two electrons in an atom can have the same set of four quantum numbers. In practical terms, each orbital can hold a maximum of two electrons with opposite spins. Hund’s Rule – Electrons will fill degenerate (equal energy) orbitals singly before pairing up. This reduces electron-electron repulsion and stabilizes the atom. These principles not only describe electron arrangements but also help predict chemical reactivity, ionization energies, and the behavior of atoms in bonding. They are essential for understanding trends in the periodic table, such as why noble gases are inert or why alkali metals are highly reactive.Additionally, quantum mechanics underpins these principles, introducing concepts like probability clouds, quantized energy levels, and wave-particle duality. A deep understanding of these principles enables accurate modeling of atoms and explains a wide range of chemical and physical properties across elements.

The principles of atomic structure govern how subatomic particles are arranged and behave within an atom. Three foundational principles guide the electron configuration of atoms: Aufbau Principle – This states that electrons occupy the lowest energy orbitals first before filling higher ones. It explains why the 1s orbital fills before 2s or 2p orbitals. Pauli Exclusion Principle – This rule states that no two electrons in an atom can have the same set of four quantum numbers. In practical terms, each orbital can hold a maximum of two electrons with opposite spins. Hund’s Rule – Electrons will fill degenerate (equal energy) orbitals singly before pairing up. This reduces electron-electron repulsion and stabilizes the atom. These principles not only describe electron arrangements but also help predict chemical reactivity, ionization energies, and the behavior of atoms in bonding. They are essential for understanding trends in the periodic table, such as why noble gases are inert or why alkali metals are highly reactive.Additionally, quantum mechanics underpins these principles, introducing concepts like probability clouds, quantized energy levels, and wave-particle duality. A deep understanding of these principles enables accurate modeling of atoms and explains a wide range of chemical and physical properties across elements.

CBSE Class 11 Chemistry Notes: Atomic Structure Simplified for Quick Revision

ATOM

Atom is electrically neutral, smallest individual particle of an element which can take part in chemical reactions.

MOLECULE

It is the smallest particle of matter which can exist in free state and is made up of atoms. Molecules having one atom in gaseous state are called monoatomic e.g. helium, argon. Molecules having two atoms are called diatomic, e.g. hydrogen gas, oxygen gas etc.

DALTON’s ATOMIC THEORY

According to this theory:
(i) Every element is made up of atoms.
(ii) An atom can neither be created nor be destroyed.
(iii) Atoms of same element are identical in mass, size and shape.
(iv) Each element is characterized by the weight of its atom.
(v) Atoms react with each other to form compounds in a simple fixed numerical ratios such as 1 : 1, 2 : 1, 1 : 2, 2 : 3 etc.

CATHODE RAYS

These are streams of electrons produced in the discharge tube containing gas (which is a poor conductor of electricity) at a very low pressure.
(i) Cathode rays originate from cathode and flow towards anode.
(ii) These are negatively charged and travel in straight line.
(iii) They cast the shadow of object in their path.
(iv) Deflected by electric and magnetic field (charged).
(v) The value of e/m (specific charge) of the particles of cathode rays does not depends upon the material of the cathode and the nature of the gas taken in the discharge tube.
(vi) No electric current flows through vacuum or the discharge tube containing gas at one atmosphere.
(vii) They produce heating effect when strike with an object.

ANODE RAYS OR CANAL RAYS

These are beams of positively charged particles. For example H⁺, He⁺ and He²⁺ etc.
(i) Anode rays do not originate from anode, these are produced in the space between anode and cathode.
(ii) Charge to mass ratio of the particles (e/m) in anode rays depends on the nature of the gas taken.
(iii) Deflection of the positive rays by the electric and magnetic field is smaller than cathode rays indicating that the positive rays have greater mass than cathode rays.

FUNDAMENTAL PARTICLES

Each atom is made up essentially of three fundamental particles electron, proton and neutron. Some other uncommon fundamental particles are:
Mesons (charge -1, +1 or 0), neutrino (negligible charge), antineutrino (negligible charge) etc.

1. Electron

Electron was discovered by J. J. Thomson (1887) by the study of cathode rays.
(i) Electron is a negatively charged particle having charge = 1.60 x 10^-19 coulombs and Mass = 9.109x10^-31 kg
(ii) The charge on the electron was determined by Millikan’s oil drop experiment.
(iii) The charge to mass (e/m) ratio of the electron was determined by Thomson using spectrometer.
(iv) Charge on one mole of electrons = 96500 C (1 Faraday)
(v) Mass of one mole of electrons = 0.55 mg

(vi) When electron is moving with velocity v, its mass is given by

m = m₀/√1-(V/C)²

where c is the velocity of light, mo is the rest mass of electron (9.1 x 10^-31kg )
Hence when electron is moving with velocity of light (v = c), its mass is infinite.
(vii)The Van der Waal’s forces of attraction increases as the number of electron in a molecule decreases.

2. Proton

Proton was discovered by Goldstein by the study of anode rays. It is a positively charged particle having charge = +1.60 x 10^-19coulomb and mass = 1.672 x 10^-27kg

3. Neutron

Neutron was discovered by Chadwick (1932), by bombarding particles (He²⁺) on beryllium atom.

(i) The charge on the neutron is zero and mass = 1.674 x 10^-27kg.
(ii) Neutron and proton are found in the central core of the atom called nucleus.

4. Nucleus

Nucleus was discovered as a result of Rutherford’s scattering experiment.
(i) It is the small central core of atom having diameter approximately 10^-15 m. Diameter of atom = 10^-10 m.
(ii) The radius of the nucleus is expressed in Fermi (1 Fermi = 10^-15 m) and is given by where A is the atomic mass and R₀ is the proportionality constant. The value of R₀ lies between 1.25 x 10^-13 cm to 1.50 x 10^-13 cm. The nuclear radii lie in the range 1.5 to 6.5 fermi.
(iii) The force that binds electrons to the nucleus is coulombic in nature.
(iv) Nucleus is responsible for entire mass of the atom.
(v) A nucleus is stable when its neutron – proton ratio is near unity.
(vi) Density of nucleus = 10¹⁴ g/cm³ or 10⁸ tonnes/cm³

ATOMIC TERMS
(i) Nuclide: Various species of atom in general.
(ii) Nucleons: Protons and neutrons are collectively called nucleons.
(iii) Mass number (A): Sum of protons and neutrons.
(iv) Atomic number (z): Number of protons in the nucleus of an atom.
Atomic mass = Total mass of protons (m_p) + Total mass of neutrons (m_n)
(v) Isobars: Atoms having same mass number but different atomic number, e.g. ₁₅P³², ₁₆S³².
(vi) Isotopes: Atoms having same atomic number but different atomic masses, e.g. ₉₂U²³⁵ , ₉₂U²³⁸.
(vii) Isotones: Atoms having same number of neutrons but different mass numbers, e.g. ₈¹⁶O, ₆¹⁴C, ₇¹⁵N.
(viii) Isosteres: Species having same number of atoms and electrons, e.g. CO₂, N₂O.
(ix) Isoelectronic species: Atoms, molecules or ions having same number of electrons, e.g. N₂, CO, CN^-.
(x) Isodiaphers: Atoms for which difference between neutrons and protons is same, e.g.

₈¹⁷O and ₇¹⁵N

(P = 8, N = 9, N - P = 1) (P = 7, N = 8, N - P = 1)
(xi) Nuclear isomers: Atoms with same atomic and mass number but different radioactive properties, e.g. uranium x(half life 1.4 min. ) and uranium z (half life 6.7 hours)
(xii) Atomic mass unit: It is equal to the 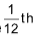of the mass of a carbon atom (₆¹²C)
Atomic weight of an element = weight of one atom of the element / 1/12 x weight of one atom of ₆¹²C
It is relative not absolute.
1 a.m.u. = 1.66 x 10^-24 g ≠ 1.66 x 10^-27 kg ≠ 931.5 meV

ATOMIC MODELS

Thomson’s Model

Atom is made up of positive charge and the negative charges are embedded in the positive charge. It is also called plum – pudding model. It could not satisfactorily explain the properties of atom.

Rutherford’s Model

In Rutherford’s ^{α -}scattering experiment, ^{α -}particles from radium or polonium were allowed to hit a thin foil of gold. Most of them passed through without undergoing any deflection (showing presence of large empty space in the atom).
Some were deflected through small angles (showing presence of small charged body in the atom).
A few were deflected back through 180° by the centre (showing that charge body is small but heavy and present at the centre).
The distance from the nucleus at which α particles return back is called the distance of closest approach and is given by r₀ = KZ₁Z₂e²/(1/2 mv²)
This experiment led to the following conclusions:
(i) Atom is spherical and mostly hollow.
(ii) Whole of the positive charge and mass of the atom is present at the small area in the centre called nucleus.
(iii) The electrons are revolving outside the nucleus.
(iii) The number of protons in the nucleus is equal to the number of electrons revolving outside nucleus.
(iv) The centrifugal force required for the circular motion of electrons is provided by the electrostatic attraction between protons and electrons.

Drawbacks of Rutherford’s model of atom

(i) Could not explain the stability of the atom.
(ii) Could not explain line spectrum of hydrogen atom.

MOSELEY EQUATION

It relates frequency of X–ray with the atomic number of element, √v = a(z-b) , where a and b are constants and z is atomic number.

ELECTROMAGNETIC WAVE THEORY

According to this theory, electromagnetic radiations are made up of electric and magnetic fields oscillating perpendicularly to each other and to the direction of propagation. All electromagnetic radiations travel with the speed of light and do not need any medium for propagation.

IMPORTANT CHARACTERISTICS OF WAVE

A wave propagate in the form of alternate crests and troughs.
(i) Wave length: It is the distance between two neighbouring crests or troughs.
(ii) Frequency: It is the number of waves passing per second. It is related to wavelength as v = c/λ or C = λ x ν
(iii) Velocity: It is the distance travelled by a wave in one second.
(iv) Amplitude (A): It is the maximum height of the crest or depth of the trough.
(v) Wave number: It is the number of wavelengths per cm. v = 1/λ

ELECTROMAGNETIC SPECTRUM

The arrangement of electromagnetic radiations in order of increasing wavelengths or decreasing frequencies is called electromagnetic spectrum.

ATOMIC SPECTRUM

(i) Absorption spectrum: Some substances absorb the energy when white light is passed from their solution or vapours and this result some dark lines in the continuous spectrum of white light. This is called absorption spectrum.

(ii) Emission spectrum: The atom loses energy in the form of radiations by the transition of electrons from higher to lower energy level. This energy corresponds to the line of specific wavelength. These lines constitute the emission spectrum.

Types of emission spectra
(a) Continuous spectra: The seven colours in the spectrum of white light are very close and constitute continuous spectra.

(b) Line spectra: The spectrum of hydrogen atom contains different lines separated by dark bands. This type of spectra is called line spectra.
Every element gives a characteristic line spectrum different from other elements. Hence, it is like the finger print of the element.

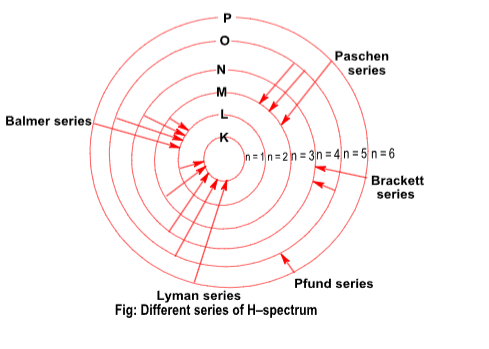
Line spectrum of H – atom: Hydrogen spectrum contains different series of lines are given in the diagram.

Note:
(i) The intensity of the spectral lines in a particular series decreases as the value of n of the outer shell increases, e.g. in Lyman series first line (n₂ = 2, n₁ = 1) has greater intensity than second line (n₂ = 3, n₁ = 1).
(ii) As the distance from the nucleus increases the energy gap between energy levels decreases.

Hydrogen like species: These have one electron like the hydrogen atom, e.g. He⁺, Li⁺⁺ etc.

Rydberg’s formula: The wave number of lines in hydrogen atom is given by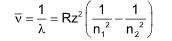

where R is called Rydberg’s constant having value 109678 cm^-1and z is the atomic number of element.

Number of Spectral Lines
(i) When the final state is the ground state (n₁ = 1) and n₂ = n

Number of spectral lines = n(n - 1)/2

(ii) When final state is not the ground state (n1 ≠ 1)

Number of spectral lines = (n₂ - n₁) (n₂ - n₁ + 1)/2 when n₂ = ∞ the line produced is called limiting line of the series.

Bohr’s Model of Atom

The main postulates of this model are:
(i) Electron revolve only in certain orbits around the nucleus called stationary states or energy levels having fixed
energies.
(ii) Electron revolve in only those energy levels for which its angular momentum is an integral multiple of h/2π, ie. mvr = nh/2π

Both energy and angular momentum of electron is quantized.

Energy of electron in n th Bohr orbit:

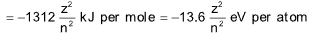
where z is the atomic number of the element.

Bohr's radius:

ε_₀is the absolute permittivity of free space or air
r_o is the radius of first Bohr orbit (r_o = 0.529 ^oA).

Velocity of electron in nth Bohr’s orbit:

Number of revolutions of electron per second in n^thorbit

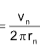
Number of waves in n^th orbit = n

When electron jumps from higher to lower level energy equal to difference of energy levels is emitted.
When electron jumps from lower to higher level energy is absorbed.
△E = E₂-E₁
where E₁ and E₂ are energies of initial and final states respectively.

Ionization energy: It is the energy absorbed when electron jumps from ground state to infinity.
I.E. = E_∞- E₁
E_∞ is taken as zero.
Electronic energy in atom is negative because when electron comes close to nucleus from infinity (zero energy) it
loses some amount of energy and an e- is held by attractive force of nucleus
Energy is additive hence, E_total =E₁ + E₂

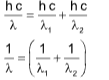
Limitations of Bohr’s theory

(i) It could not explain the spectra of multi electron atoms.
(ii) It could not explain the splitting of spectral lines into a group of fine lines under the influence of electric field (Stark effect) and magnetic field (Zeeman effect).
(iii) Bohr’s theory is not in agreement with the Heisenberg’s uncertainty principle.

Sommerfield’s extension of Bohr’s theory

To account for the fine spectrum of H – atom Sommerfield proposed that electron move in elliptical orbits and the
nucleus is situated at one of the foci.

PLANCK’S QUANTUM THEORY
According to this a hot body emits radiation energy not continuously but in small packets called quanta. Energy of each quantum is given by E=hv and for ‘n’ quanta E_total=nhv
where ^v is the frequency of light and h is Planck’s constant having value 6.624 x 10^-34 Js.

EINSTEIN’S EQUATION
It is E = mc² , where ‘E’ is the energy of photon, ‘m’ is the mass and ‘c’ is the velocity of photon.

PHOTOELECTRIC EFFECT
When light of certain frequency ( threshold frequency, ν_₀) is incident on a metal surface, electrons are ejected from the surface. If the incident radiation have frequency v > (ν_₀), the difference of energy (hv - hν_₀) is converted to kinetic energy of photoelectrons.

1/2 mv₂ = hv - hv₀ where hv₀ is the minimum energy required for the emission of photoelectrons and is called work function of metal.
No electron is ejected if the energy of incident light is less than the work function of a given metal. The number of
electrons ejected depends upon the intensity and velocity and kinetic energy of photoelectrons depend upon the
frequency of incident radiations.

Ex.: In the photo electric effect the energy of emitted electrons is
(A) greater than the incident photon
(B) same as that of incident photon
(C) smaller than incident photon
(D) none of these

Solution: (C).

K. E. of electrons = hv-hv_o (smaller than incident photon)

Ex.: The work function of a metal is 4.2 eV. If radiation of 2000 A fall on the metal, the K.E. of fastest photoelectron is
(A) 1.6 x 10^-19 J

(B) 16 x 10^-10 J
(C) 3.2 x 10^-19 J

(D) 6.4 x 10^-10 J

Solution: (C).

hc/λ = w₀ + K.E. where wo is the work function.

Hence K.E = hc/λ - w⁰ = 3.2 x 10^-18 J

COMPTON EFFECT

When monochromatic X – rays are allowed to fall on some light element, X – ray interact with electrons and the scattered X – rays have less frequency than incident X – rays. This is called Compton’s effect.

DUAL NATURE OF MATTER AND RADIATIONS

de – Broglie (1924) suggested that all material particles posses wave nature as well as particle nature and gave the equation called de – Broglie equation.

λ = h/mv = h/p
where λ is the wavelength, m is mass, v is the velocity of the particle and h is the Planck’s constant.
The wave nature of electron is confirmed by Davisson and Germer’s experiment and by Thomson’s experiment.
The particle nature is confirmed by photoelectric effect and scintillation method.

HEISENBERG’S UNCERTAINTY OR INDETERMINACY PRINCIPLE

It states that it is impossible to measure simultaneously the exact position and the exact momentum of a microscopic moving body. The uncertainty in position (△x) and uncertainty in momentum (△p) are related as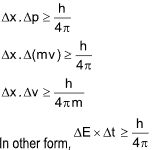

where h is Planck’s constant, E is energy and t is time
de – Broglie and uncertainty principle both have significance only for microscopic particles and no significance in everyday life (macroscopic particles).

WAVE OR QUANTUM MECHANICAL MODEL OF ATOM

This model is proposed by Schrodinger (1920) and is based on dual nature of electron and Heisenberg’s uncertainty principle. He derived an equation which describes the wave motion of electron in three dimensional space. This is known as Schrodinger wave equation

Square of the wave function 𝚿2 gives the probability of finding electrons within a small three dimensional space.
The acceptable solutions of the above equation for energy E are called Eigen values and corresponding wave functions 𝚿 are called Eigen functions.

Atomic Orbital

It is the three dimensional space around the nucleus within which the probability of finding electrons is maximum.

QUANTUM NUMBERS

These are the set of four numbers which provide us the complete information about an electron in the atom, i.e. its energy, the orbit in which it is present and the orientation of that orbital, direction of the spin of electron and its distance from the nucleus.
Note: All quantum numbers are the result of solution of Schrodinger equation except spin quantum number.

(i) Principle quantum number (n): It represents the main shell and gives the idea about the energy and distance of electron from the nucleus. It was given by Bohr.

(ii) Azimuthal or angular quantum number (l): It represents the number of subshells in the main shell. It was given by Sommerfield and can have a value from 0 to (n -1).
𝓁 = 0 s – subshell
𝓁 = 1 p – subshell
𝓁 = 2 d – subshell
𝓁 = 3 f – subshell
𝓁 = 4 g – subshell
The orbital angular momentum of the electron is given by

(iii) Magnetic quantum number (m): It represents the number of orbitals in a subshell and orientation of electron clouds (orbitals). Magnetic quantum number can have values from -𝓁 to +𝓁 including zero. It was discovered by Lande.
The total possible values of m = number of orbitals in a subshell = 2𝓁 +1
Maximum number of electrons present in a subshell = 2(2𝓁 +1)

(iv) Spin quantum number (s): It was given by Schmidt and represents the direction of electron spin around its axis.

For clockwise
For anticlockwise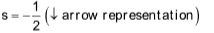

Spin angular momentum is given by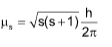

For n number of unpaired electrons 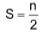where S is the total spin.

Spin magnetic moment is given by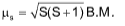

Number of subshells in n^th shell = n
Number of orbitals in n^th shell = n²
Maximum number of electrons in a shell = 2n²
Maximum number of electrons in an orbital = 2

SHAPES OF ATOMIC ORBITALS

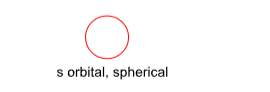
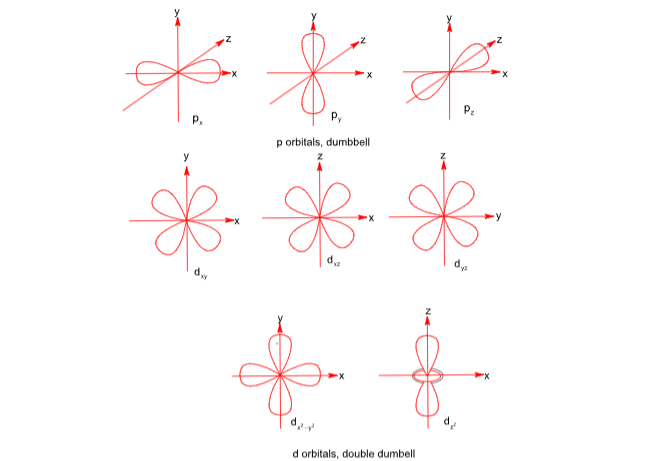
Note: (i) d – orbital which does not have four lobes is dz2 .
(ii) d – orbital whose lobes lie along the axis is dx2-y2 .
(iii) The space in which probability of finding electron is zero is called node.

Spherical or radial nodes :

It is the spherical surface within orbital in which probability of finding electron is zero. The number of radial nodes in an orbital = n-𝓁-1 e.g. 3p orbital (n = 3, 𝓁 = 1) has one spherical node.

Nodal plane or angular node :

It is the plane passing through the nucleus in which the probability of finding electrons is zero.
Number of angular nodes (nodal planes) = 𝓁
e.g. a d – orbital (𝓁 = 2) has two nodal planes.

Total nodes = radial nodes + angular nodes = (n – 1)

PAULI’s EXCLUSION PRINCIPLE

It states that no two electrons in an atom can have the same set of four quantum numbers or one orbital can have
only two electrons with opposite spins.

AUFBAU PRINCIPLE

It states that in the ground state of element orbitals are filled in order of their increasing energies starting with the
orbital of lowest energy.
The order of increasing energies and order of filling of various subshells is
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p and so on.
The subshell with lowest (n+ℓ) value has lowest energy and has been filled first.
If two subshells have same value for (n+ℓ) , the subshell with lowest value of n is filled first.

HUND’s RULE OF MAXIMUM MULTIPLICITY

It states that electronic pairing in orbitals of same energy (degenerate orbitals) will not take place unless all the
available orbitals of given subshell contain one electron each with parallel spin.

In case of hydrogen atom, the energies of atomic orbitals increases as
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f and so on.
Half filled and fully filled electronic configurations are more stable because of
(i) greater symmetry (ii) greater exchange energy

ELECTRONIC CONFIGURATION OF ATOMS

Zn (Z = 30): 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s²
[Ar] 3d¹⁰ 4s²
Cl (Z = 17): 1s² 2s² 2p⁶ 3s² 3p⁵
[Ne] 3s²3p⁵
Electronic configuration of some special elements
Cr (Z = 24): [Ar] 3d⁵ 4s¹
Cu (Z = 29): [Ar] 3d¹⁰ 4s¹
Pd (Z = 46): [Kr] 4d¹⁰ 5s⁰
La (Z = 57): [Xe] 6s² 5d¹ (not 4f¹)
Ce (Z = 58): [Xe] 6s² 5d¹ 4f¹
Ac (Z = 89): [Rn] 7s² 6d¹ (not 5f¹)

Electronic configuration of ions

Fe (Z = 26) : [Ar] 4s² 3d⁶
Fe²⁺ : [Ar] 4s⁰ 3d⁶
O (Z = 8) : 1s² 2s² 2p⁴
O²¹ : 1s² 2s² 2p⁶
When the molecule having all paired electrons absorbs energy, the following changes may happen.

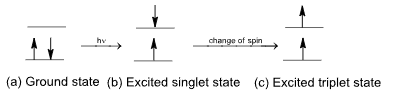
SPIN MULTIPLICITY

It is given by 2s + 1 where s is the total spin.
For fig. (b),
Spin multiplicity = 2 s + 1 = 0 + 1 = 1 (singlet)
For fig. (c),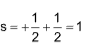
Spin multiplicity = 2 s + 1 = 2 x 1 + 1 = 3 (triplet)

Frequently Asked Questions

The development of atomic models over time has shaped our current understanding of atomic structure. Each model was proposed based on experimental observations and helped address the shortcomings of previous theories. Here are five significant atomic models:

Dalton’s Model (1803): Proposed that atoms are indivisible, solid spheres. While groundbreaking, this model couldn't explain atomic reactions or the presence of subatomic particles.
Thomson’s Model (1897): Known as the "plum pudding model," it described the atom as a positively charged sphere embedded with negatively charged electrons, like raisins in a pudding. This model introduced electrons but lacked a structured nucleus.
Rutherford’s Model (1911): Through the gold foil experiment, Rutherford concluded that atoms have a small, dense, positively charged nucleus with electrons orbiting around it. This model introduced the nuclear concept but couldn’t explain electron stability.
Bohr’s Model (1913): Niels Bohr added that electrons move in fixed energy levels or orbits and could jump between levels by absorbing or emitting energy. This model worked well for hydrogen but failed for more complex atoms.
Quantum Mechanical Model (1926): Based on Schrödinger’s wave equation, this model describes electrons as existing in probability clouds called orbitals. It incorporates the Heisenberg uncertainty principle and accurately predicts chemical behavior.

Each model contributed crucial insights, with the quantum mechanical model currently accepted as the most accurate representation of atomic structure.

Solving problems related to atomic structure involves applying concepts such as electron configuration, quantum numbers, isotopes, and periodic trends. Here’s a step-by-step guide:

Identify Atomic Number (Z): This tells you the number of protons and, in a neutral atom, the number of electrons.
Calculate Neutrons: Use the mass number (A) to subtract the atomic number (Z), i.e., Neutrons = A – Z.
Write Electron Configuration: Distribute electrons into orbitals based on the Aufbau principle, e.g., Oxygen (Z=8) → 1s² 2s² 2p⁴.
Assign Quantum Numbers: For any given electron, determine the four quantum numbers (n, l, m, s) that describe its energy level, subshell, orbital, and spin.
Apply Periodic Trends: Use atomic structure to predict trends such as electronegativity, atomic radius, and ionization energy. For example, atoms with more protons have smaller radii due to greater nuclear attraction.
Interpret Isotopes and Ions: For ions, add or subtract electrons. For isotopes, identify the same number of protons but different numbers of neutrons.

Practicing MCQs and numerical problems—like finding the number of electrons in ions or determining atomic radii differences—can strengthen your skills. Use visual tools like orbital diagrams and electron cloud sketches to aid conceptual understanding.

S.no	Formulas List
1.	Atomic Structure
2.	Some Basic Concepts of chemistry
3.	Gaseous State
4.	Periodic Properties
5.	Chemical Bonding
6.	Thermodynamics & Thermochemistry
7.	Chemical Equilibrium
8.	Ionic Equilibrium
9.	Surface Chemistry
10.	S-block elements and Hydrogen

Atomic Structure

ATOM

MOLECULE

DALTON’s ATOMIC THEORY

CATHODE RAYS

ANODE RAYS OR CANAL RAYS

FUNDAMENTAL PARTICLES

1. Electron

2. Proton

3. Neutron

4. Nucleus

ATOMIC MODELS

Thomson’s Model

Rutherford’s Model

Drawbacks of Rutherford’s model of atom

MOSELEY EQUATION

ELECTROMAGNETIC WAVE THEORY

IMPORTANT CHARACTERISTICS OF WAVE

ELECTROMAGNETIC SPECTRUM

ATOMIC SPECTRUM

Bohr’s Model of Atom

Energy of electron in n th Bohr orbit:

Bohr's radius:

Velocity of electron in nth Bohr’s orbit:

Limitations of Bohr’s theory

Sommerfield’s extension of Bohr’s theory

DUAL NATURE OF MATTER AND RADIATIONS

HEISENBERG’S UNCERTAINTY OR INDETERMINACY PRINCIPLE

WAVE OR QUANTUM MECHANICAL MODEL OF ATOM

Atomic Orbital

QUANTUM NUMBERS

SHAPES OF ATOMIC ORBITALS

Spherical or radial nodes :

Nodal plane or angular node :

PAULI’s EXCLUSION PRINCIPLE

AUFBAU PRINCIPLE

HUND’s RULE OF MAXIMUM MULTIPLICITY

ELECTRONIC CONFIGURATION OF ATOMS

Electronic configuration of ions

SPIN MULTIPLICITY

Frequently Asked Questions

Related Links

Become one of thousands of satisfied students!

Frequently Asked Questions