Introduction
Gases have the following general characteristics:
(i) Gases are highly compressible.
(ii) Gases expand without limit.
(iii) Gases exert pressure on the walls of the container uniformly in all directions.
(iv) Gases diffuse rapidly through each other to form a homogeneous mixture.
(v) The characteristics of gases are described fully in terms of four parameters
(a) The volume (V) of the gas.
(b) Its pressure (P).
(c) Its temperature (T)
(d) The amount of the gas (i.e. mass or number of moles).
(vi) All gases obey certain laws called gas laws.
GAS LAWS
(i) Boyle’s Law
This laws states that at constant temperature and for a given mass of gas, the volume of a sample of a gas varies inversely with the pressure.
V ∝ 1/P or V = K/P or PV = K
Mathematically, it can be written as,
P1V1 = P2V2 = P3V3
Graphically, it can be represented by the following
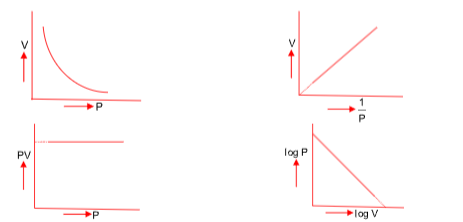
(ii) Charle’s law
This law states that “The volume of a given amount of a gas at constant pressure varies directly to its absolute temperature, i.e.V α T”.
(iii) Pressure temperature law
This law states that–
At constant volume, the pressure of a given amount of a gas is directly proportional to its absolute temperature. Mathematically,
P α T (If volume is kept constant)
Ex.: Mountaineers carry oxygen cylinders with them because
(A) density of air is high at the altitudes
(B) density of air is low at the altitudes
(C) air is less pure at the altitudes
(D) air contains on oxygen at the altitudes
Solution: (B).
Less oxygen is available at altitude because density of air is low
Ex.: When gas is compressed at constant temperature
(A) the speeds of the molecules increase
(B) the collisions between the molecules increase
(C) the speeds of the molecules decrease
(D) the collisions between the molecules decrease
Solution: (B).
On compressing the gas, pressure increases and hence the collisions between the molecules increase
Ideal Gas Equation
This equation is obtained by combining Boyle’s and Charle’s laws.
V ∝ 1/P. .....(i) (At constant temperature and definite mass)
V α T .....(ii) (At constant pressure and definite mass)
Combining (i) and (ii), we get
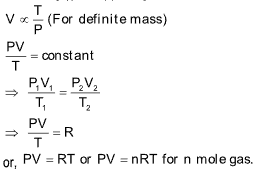
OPEN VESSEL CONCEPT
In open vessel of a gas, pressure and volume are always constant.
PV = n1RT1
so, n1T1 = n2T2
DRY AND MOIST GAS
Pdry = Pmoist – aqueous tension or vapour pressure of water
Relative humidity = Partial pressure of water in air/ Vapour pressure off water
Ex.: The density of gas is 1.4 g/ml at one atmosphere pressure and 27oC. At what pressure will the gas have density thrice this value, the temperature is kept constant?
(A) same pressure
(B) 2 atmosphere
(C) 3 atmosphere
(D) 4.2 atmosphere
Solution: (C).
Dalton's Law of Partial Pressures
This law states that, at a given temperature, the total pressure exerted by two or more non–reacting gases occupying a definite volume is equal to the sum of the partial pressures of the component gases. Mathematically,
PT = PA + PB + PC + ……
PA = XA x PT
Partial pressure of a component = Mole fraction x Total pressure
AMAGAT LAW OF PARTIAL VOLUME
Total volume of a mixture of non–reacting gases at constant temperature and pressure is equal to sum of individual volumes (partial volumes) of constituent gases.
V = Σ V1 = V1 + V2 + ...........+ Vn
DIFFUSION OF GASES
When two gases are brought together, they mix with each other instantly. This ability of a gases to mix instantly and to form a homogeneous mixture is known as diffusion.
Effusion
It is a process in which a gas is allowed to escape under pressure through a fine orifice or a small aperture made in a wall of a closed container.
Graham’s law of diffusion or effusion
The law states that “At constant pressure and temperature, the rate of diffusion or effusion of a gas is inversely proportional to the square root of it’s density”.
Rate of diffusion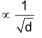 
or,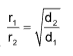 
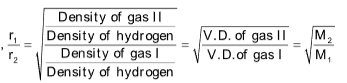
when pressure is not constant
......(i)
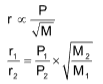
r α P ......(ii)
Combination of these equations gives,
KINETIC THEORY OF IDEAL GASES
This theory was a generalization of facts about ideal gases. It was presented by Bernoulli in 1738 and developed in 1860 by Clausius & Boltzmann. Postulates of kinetic theory of gases are–
(i) Gases are made up of small structural units called atoms or molecules. Volume of individual atom or molecule is considered negligible.
(ii) Gas molecules are always in rapid random motion colliding with each other and with the wall of container.
(iii) Collision among gas molecule is perfectly elastic.
(iv) Gas molecules neither attract nor repel each other.
(v) Pressure exerted by gas is due to collision of gas molecules with the wall of container.
(vi) Kinetic energy of gas molecules depends only on absolute temperature.
Kinetic energy α Absolute temperature
(vii) The force of gravity has no effect on the speed of gas molecule.
Kinetic gas equation
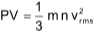
where, P = Pressure of the gas
V = Volume of gas
m = Mass of a molecule
n = Number of molecules present in given mass of gas
Vrms = Root mean square speed
Root mean square speed
The value of R should be 8.314 JK–1mol–1 and M should be in kg.
Kinetic energy
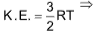Kinetic energy per mole
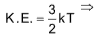Kinetic energy per molecule
where, k = Boltzmann constant
= 1.38 x 10-23 J/K/molecule
Other molecular speeds
(a) Average speed: It is arithmetic mean of the various speeds of the molecules.
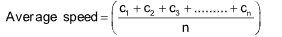
It is equal to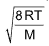 
It is related to RMS as
Average speed = 0.9213 x RMS speed
RMS speed = 1.085 x Average speed
(b) Most Probable speed: This is defined as the speed possessed by maximum number of molecules of a gas at a given temperature.
It is equal to 
It is related to RMS as
Most probable speed = 0.816 RMS
RMS = 1.224 MPS
The three kinds of molecular speeds are related to each other as:
Most probable speed: Average speed: RMS speed
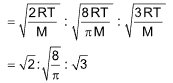
= 1: 1.128: 1.224
DISTRIBUTION OF MOLECULAR SPEEDS
An increase in temperature also ‘widens’ the distribution of molecular speeds, i.e. at a higher temperature, there are more molecules having much lower speed than the average speed and also more molecules having much higher speed than the average speed compared with the corresponding numbers at lower temperature.
Note: All areas within each curve are equal representing equal number of moles.
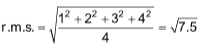
Example 4 : Four molecules of a gas have speeds of 1, 2, 3, 4 cm/sec respectively.
The root mean square velocity is
Solution: (A).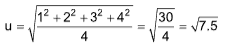
DEVIATION FROM IDEAL GAS BEHAVIOUR
van der WAAL’s EQUATION
It is observed that deviations from gas laws are high under high pressures and low temperatures.
van der Waal suggested that these deviations are due to the following two faulty assumptions in the kinetic theory of the gases.
(i) Actual volume of the gas molecules is negligible as compared to the total volume of gas.
(ii) Intermolecular attractions are not present in gas.
According to van der Waal’s theory, in case of real gases, molecules do have a volume and also exert intermolecular attractions especially when the pressure is high and temperature is low. He suggested two corrections
(a) Volume correction: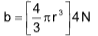 
‘b’ is termed as the excluded volume which is constant and characteristic for each gas.
The excluded volume (b) is actually four times the actual volume of gas molecules.
where, ‘r’ – radius of gas molecule
N – Avogadro’s number
(b) Pressure correction: In real gas, if forces of attraction are in picture, then observed pressure will be less than the ideal pressure.
Pidol = Pobs + P'
where = Pressure correction
P' α Total attractive force
P' α d2 [d is the density of gas]
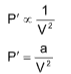
where ‘a’ is a constant depending upon the nature of gas and V is the volume of 1 mole of gas.
Pidol = Pobs
So, ideal gas equation can be written as
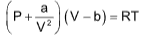
For ‘n’ moles of gas
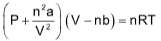
COMPRESSIBILITY FACTOR
To display the deviation of a gas from ideal behaviour clearly, the ratio of the observed molar volume ‘V’, to the ideal molar volume 
is plotted against pressure at constant temperature. This ratio is called the compressibility factor (Z).
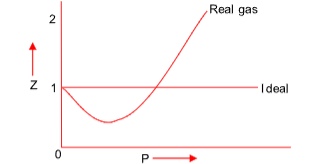
(i) For an ideal gas, Z = 1 and is independent of P and T.
(ii) For real gas Z ≠ 1 and depends on P and T.
If Z < 1 or Z > 1, the gas is more or less compressible to an ideal gas respectively.
SOME IMPORTANT FACTS
(i) At low pressure, the gas equation can be written as
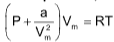(P ↓,Vm ↑,so b is negligible)
or,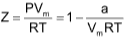 
where Z is compressibility factor. It’s value at low P is less than 1. On increasing the pressure in this region, the value of the term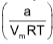 
increases as Vm is inversely proportional to P. Consequently, Z decreases with increase of P.
(ii) At high pressure, the term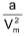 
may be considered negligible in comparison to P. Thus, we have,
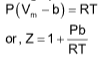
Hence, Z is greater than 1 and it increases linearly with pressure at constant temperature and it decreases with increase of temperature at constant pressure.
For H2 & He, the value of ‘a’ is extremely small as they are difficult to liquefy. Thus we have the equation of state as P(Vm - b ) = RT Hence, Z is always greater than 1 and increases with increase in P.
Example 5 : The value of van der Waal’s constant ‘a’ is minimum for:
(A )helium (B) hydrogen
(C)nitrogen (D) chlorine
Solution: (A). ‘a’ is a measure of intermolecular forces of attraction which are minimum for helium.
Example 6 :Certain volume of gas exerts some pressure on walls of container at a constant
temperature. It has been found that by reducing the volume of the gas to half of its
original value, the pressure becomes twice that of initial value at constant
temperature. This because
(A) the weight of the gas increases with pressure
(B) velocity of gas molecules decreases
(C) more number of gas molecules strike the surface per second
(D) gas molecules attract one another
Solution: (C). As the volume is decreased, pressure increase because more number of molecular strike the surface per second.
Boyle’s temperature (TB)
For each gas, there is a certain temperature, known as Boyle’s temperature at which PV is almost equal to RT upto moderate pressure. It can be shown that,
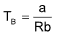
Critical temperature (TC)
It is defined as the characteristic temperature of a given gas below which a continuous increase in pressure will bring liquification of gas and above which no liquification is possible although pressure may be increased manifolds.
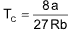
Boyle’s temperature (TB) of a gas is always higher than it’s critical temperature (TC).
Example 7 : The relationship between Pc, Vc and Tc is
Solution: (D).
The relationship between critical constants is
POINTS TO PONDER
1. Boyle’s law states that
V ∝ 1/P at constant temperature for a given mass of gas.
2. Charle’s law
V α T (K) (at constant pressure for a given mass of gas)
3. Pressure-Temperature law (Gay Lussac law)
P α T (at constant volume)
4. Ideal gas equation
PV = nRT
5. Dalton’s law of partial pressure
PT = PA + PB + PC ...
where PT = total presure of gases
PA, PB, PC = Partial pressure of gases A, B and C respectively
6. Grahm’s law of diffusion
.png)
7. Kinetic gas equation
.png)
where P = Pressure of the gas
V = Volume of the gas
m = mass of a molecule
n = number of molecular present in given mass of gas
Vrms = Root mean square speed.
8. Root mena square speed
.png)
Average speed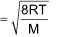 
Most probable speed .png)
9. Average speed : most probable speed : root mean square speed = 1.128 : 1 : 1.224
10. van der Waal’s equation
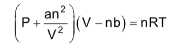
11. Compressibility factor
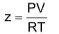
(i) for an ideal gas, z = 1 and is independent of P and T.
(ii) for real gases, z ≠ 1 and depneds on P and T.
(a) if z < 1; gas is more compressible
(b) if z > 1; gase is less compressible
12. Boyle’s temperature
.png)
where TB = Boyle’s temperature
13. Critical temperature
.png)
SOLVED EXAMPLES
1. Four one litre flasks are separately filled with the gases O2, F2, CH4 and CO2 under the same conditions. The ratio of number of molecules in these gases are
(A) 2 : 2 : 4 : 3
(B) 1 : 1 : 1 : 1
(C) 1 : 2 : 3 : 4
(D) 2 : 2 : 3 : 4
Sol. (B).
Equal volume of all gases under similar conditions of T and P contain same number of molecules.
2. The temperature at which the r.m.s. velocity of carbon dioxide becomes the same as that of nitrogen at 21oC is
(A) 462oC
(B) 273 K
(C) 189oC
(D) 546 K
3. Four molecules of a gas have speeds of 1, 2, 3, 4 cms–1 respectively. The root mean square velocity is
(A) 
(B) 
(C) 30
(D) 15
Sol. (A).
4. V vs T curves at constant pressure P1 and P2 for an ideal gas are shown below:
.png)
Which is correct?
(A) P1 > P2
(B) P1 < P2
(C) P1 = P2
(D) All of the above
Sol. (B).
At a constant temperature, the product of PV is constant.
For a given temperature T as V1 is more hence P2 shall be greater than P1.
5. Two samples of air 1 cm3 each are taken. Sample A is kept at temperature T0 at sea level and another sample B at a height where pressure is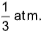 
The absolute temperature of B at that height is
(A) 
(B) T0
(C) 3T0
(D) Cannot be determined from above data
Sol. (D).
The data is insufficient to calculate.
6. The molar volume of CO2 is maximum at
(A) NTP
(B) 0oC and 2.0 atm
(C) 127oC and 1 atm
(D) 273oC and 2 atm
Sol. (C).
The molar volume of CO2 at 127oC and 1 atm is
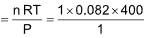
= 32.8 L
7. The numerical value of RT/PV for a gas at critical condition is ………… times of RT/PV at normal conditions
(A) 4
(B) 3/8
(C) 8/3
(D) 1/4
Sol. (C). At critical temperature,
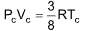
Hence, RT/PV for a gas at critical temperature = 8/3 that of gas at N.T.P.
8. The partial pressure of hydrogen in a flask containing 2g of H2 and 32g of SO2 is
(A) 1/16 of total pressure
(B) 1/2 of total pressure
(C) 2/3 of total pressure
(D) 1/8 of total pressure
Sol. (C).
Moles of H2 = 2/2=1, moles of SO2 = 32/64 = 0.5
Total moles = 1 + 0.5 = 1.5
Let total pressure be P
Pressure of 1.5 moles = P
Pressure of 1 mol P = P/1.5 = P/3/2 = 2P/3
9. A perfect gas undergoes isothermal compression, which gives its volume by 2.20 L. The final pressure and volume of the gas are 3.78x103 torr and 4.65 L, respectively. Calculate the original pressure of the gas in atm.
(A) 3.38 atm (B) 4.28 atm
(C) 2.38 (D) None of the above
Sol. (A). Boyle’s law in the form pfVf = piVi can be solved for either initial or final pressure,
Hence pi =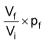 
pi =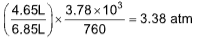 
10. Under what conditions will a pure sample of an ideal gas not only exhibit a pressure of 1 atm but also a concentration of 1 mole/litre? [R = 0.082 lit atm/mol/deg]
(A) at STP (B) when v = 22.4 lts
(C) when T = 12 K (D) impossible under any conditions
Sol. (C).
PV = nRT
or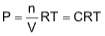 
Hence 1 = 1 x 0.082 x T is .png)