Thermodynamics & Thermochemistry

INTRODUCTION 

The branch of science which deals with energy changes during chemical reaction is called chemical energetics and the branch which deals with heat changes in a chemical reaction is called thermochemistry.

This branch also help us to predict spontaneous nature of any thermodynamic process.

TERMS USED IN THERMODYNAMICS

System

The system is any region of space being investigated.

(i) Closed system: A system which can only exchange energy but not matter with surroundings.

(ii) Open system: A system which can exchange both matter and energy with the surrounding.

(iii) Isolated system: A system which can neither exchange matter nor energy with the surroundings.

Surrounding

The surroundings are considered to be all other matter that can interact with the system. System + surrounding = Universe

Thermodynamics Properties

(i) Extensive property: Those variables whose values in any part of the divided system are different from the values of the entire system are called extensive properties, e.g. volume, energy, heat capacity, enthalpy, entropy etc.

State Functions

Fundamental properties which determine the state of a system are referred to as state functions. The state properties do not depend upon the path followed, the change in these properties depend only on initial and final state of system, e.g. pressure, volume, temperature, enthalpy etc. 

Thermodynamic Processes

Any systematic change in thermodynamic state functions of any system is known as thermodynamic process

(i) Isothermal process: This occurs under constant temperature condition.
(ii) Isobaric process: This occurs under constant pressure condition.
(iii) Isochoric process: This occurs under constant volume condition.
(iv) Adiabatic process: This occurs under the condition that heat can neither be added to nor removed from the system. These processes are also isoentropic processes.

Internal Energy 

It is the sum of all forms of energy of all the particles present in the system at a particular temperature. It includes translational energy, vibrational energy, rotation energy etc. The exact value of this energy is not known as it includes all types of energies of molecules constituting the given mass of matter. It is denoted by U(SI) or E.

First Law of thermodynamics

The net energy change of a closed system is equal to heat absorbed plus the work done on the system. In other words the total energy of an isolated system remains conserved ΔE = ΔQ + ΔW
where, ΔQ = heat absorbed ΔE = change in internal energy ΔW = work done on the system

Enthalpy or Heat Content

The energy stored in a substance that can be available in the form of heat.
H = E + PV ΔH = ΔE + PΔV = ΔE + Δn_gRT
Δn_g = (n_p - n_r) where n_p = number of moles of gaseous products
n_r = number of moles of gaseous reactants

Example 1 : If ΔH is the enthalpy change and ΔE the change in internal energy accompanying a gaseous reaction then 

(A) ΔH is always less than ΔE

(B) ΔH is always greater than ΔE

(C) ΔH is less than ΔE if the number of moles of gaseous products is greater than the number of moles of gaseous reactants.

(D) ΔH is less than ΔE if the number of moles of gaseous products is less than the number of moles of gaseous reactants

Solution: (D). As, ΔH = ΔE + Δn_gRT
ΔH value is less than or greater than ΔE depending on the value of Δn_g which is the change in number of moles of the gaseous components.
As result (A), (B) cannot be true
ΔH<ΔE when Δn_g <0, hence (C) is also false only (D) is correct

Heat Capacity

Heat capacity of a system is defined as the quantity of heat required to raise the temperature of the system by one degree.

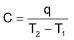
where, C = Heat capacity

q = Heat absorbed
T₁ = Initial temperature
T₂ = Final temperature

If the amount of substance taken is 1 gm then C is called specific heat capacity and if the amount of substance taken is 1 mole then C is called molar heat capacity.

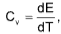at constant volume 
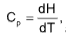at constant pressure 

Note: (i) Lighter elements have higher specific heat capacity and vice – versa. Specific heat of same substance in solid, liquid or gaseous state will be different.

(ii) Specific heat of water in cal / goC is 1, that of ice is 0.5, and that of steam is 0.47.

(iii) Boiling point of a liquid rises on increasing pressure whereas melting point can increases in some cases and can decreases also depending upon contraction and extension on melting. e.g. Melting points of ice and rubber (which contract on melting) fall with increase in pressure. Melting point of wax and sulphur (which expand on melting) rise with rise in pressure.

(iv) At Boyle’s temperature, all real gases behave like a perfect gas.

(v) At low pressure and high temperature a gas may show behaviour of ideal gas.
(vi) A real gas spread in a very large volume also behaves as a real gas.
(vii) Saturated vapours do not obey gas laws whereas unsaturated vapours obey gas laws.

Work done in isothermal reversible process

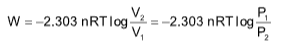
where, V₁ = initial volume and V₂ = final volume

Work done in adiabatic reverseible expansion

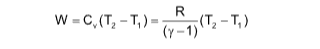
Adiabatic relations

 PV^γ = constant
TV^γ-1 = constant

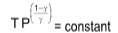
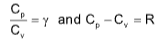
where, 
C_p = specific heat capacity at constant pressure
C_v = specific heat capacity at constant volume
R = universal gas constant
γ = specific heat ratio of gas

KIRCHHOFF’S EQUATION Kirchhoff's Equation

ΔH₂ - ΔH₁ = ΔC_p(T₁ - T₂)(at constant pressure)
ΔE₂ - ΔE₁ = ΔC_p(T₂ - T₁)(at constant volume)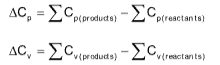
 

Ex.: A gas expands from 1.5 L to 6.5 L against a constant pressure of 0.5 atm and during this process the gas also absorbs 100 J of heat. The change in the internal energy of the gas is

(A) 153.3 J

(B) 353.3 J

(C) –153.3 J

(D) –353.3 J

Solution: (C).

 ΔE = q-w

=100J - (0.5 atm)(6.5L - 1.5L) =100J - (2.5 atm L)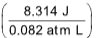

= –153.3 J

Example 3 : If a gas adiabatically changes from 1.0 L to 12.0 L against a constant pressure of 0.75 atm. The ΔE of the gas is

(A) –853.9 J

(B) 835.9 J

(C) 853.9 J

(D) –835.9 J

Solution: (D). 

ΔE = W = -p_extΔV for adiabatic process
= -(0.75 atm)(12.0 L - 1.0 L)

Example 4 : Which of the statement is correct?

(A) Slope of adiabatic P–V curve will be same as that of isothermal one

(B) Slope of adiabatic P–V curve is smaller than that in isothermal one

(C) Slope of adiabatic P–V curve is larger than that in isothermal one

(D) Slope of adiabatic P–V curve may be smaller or larger depending on the value V

Solution: (C).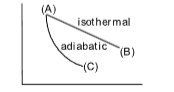

Slope of PV curve, for isothermal process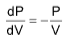
Slope of PV curve for adiabatic process 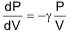As eg > 1;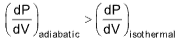 

TYPES OF ENTHALPIES

Enthalpy of combustion

 CH₄(g) + 2O₂(g)⟶CO₂(g) + 2H₂O(g); ΔH = -890.4 kJ mol^-1
Enthalpy of combustion of CH₄ = –890.4 kJ mol^–1
i.e. heat released for 1 mole of substance.

Example 5 : The molar enthalpies of combustion of C_2H2(g), C(graphite) and H₂(g) are –1300, –394 and –286 kJ mol^–1 respectively. The standard enthalpy of formation of C₂H₂(g) is

(A) 226 kJ mol^–1 

(B) –226 kJ mol^–1

(C) –620 kJ mol^–1

(D) 620 kJ mol^–1

Solution: (A). It is given that,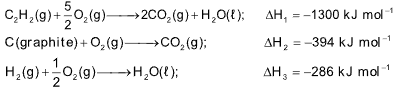

Hence, for the equation
2C(graphite)+ H₂(g)⟶C₂H₂(g)
ΔH = 2VH₂ + ΔH₃ - ΔH₁ =[-2 x 394 - 286 +(1300) ]kJ mol^-1] = 226 kJ mo^l–1

Enthalpy of neutralization

 H⁺(aq)⁺ OH^-(aq)⟶H₂O(ℓ); ΔH = -57.1 kJ mol^-1
Heat evolved / absorbed when 1 gm equivalent of both reacted.

Enthalpy of hydration

Heat evolved/ absorbed when 1 mol of anhydrous substance convert into hydrated formed 
CuSO₄(s)+ 5H₂O――⟶CuSO₄.5H₂O(s);ΔH = -78.2 kJ mol^-1

Enthalpy change during phase transitions

Heat of fusion

Heat evolved / absorbed when 1 mol of solid directly converts liquid at constant temperature.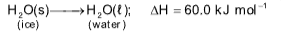 

Heat of vaporization

Heat evolved / absorbed when 1 mol of liquid converts into gas (vapour) at constant temperature.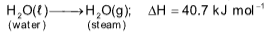 

Heat of sublimation

Heat evolved / absorbed when 1 mol of solid directly converts into gas (vapour) at constant temperature. 
I₂(S)⟶I₂(g); ΔH = 62.39 kJ mol-1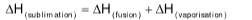 

HESS’s LAW OF CONSTANT HEAT SUMMATION

This law states that “the resultant enthalpy change in a reaction is the same whether it occurs one or several steps”.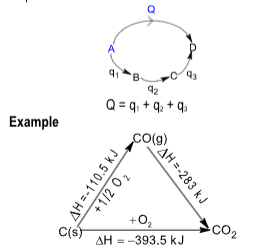

BOND ENERGY (B.E.)

It is the defined as the enthalpy change when a mole of gaseous molecules separates into constituent gas atoms.
H₂(g)――⟶2H₁ ΔH_H-H = 436 kJ mol^-1

Note: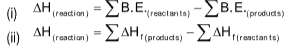

Example 6 : The enthalpy of combustion of H₂(g) to give H₂O(g) is –249 kJ mol^–1 
and bond enthalpies of H–H and O=O are 433 kJ mol^–1 and 492 kJ 
mol^–1 respectively. The bond enthalpy of O–H is

(A) 464 kJ mol^–1 

(B) –464 kJ mol^–1

(C) 232 kJ mol^–1

(D) –232 kJ mol^–1

Solution: (A). For the equation,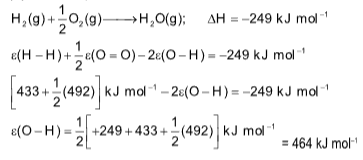

ENTROPY

Entropy is a thermodynamic quantity which is a measure of the randomness or disorder of the molecules of the system.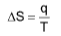

where, q – amount of heat evolved and absorbed at constant temperature
T – temperature
Entropy is a measure of randomness of a system.
ΔS(total) = ΔS(system)+ ΔS(surroundings)
(i) Spontaneous process,ΔS(total) > 0
(ii) Non – spontaneous process,ΔS(total)> 0
(iii) Equilibrium, ΔS(total)= 0

SECOND LAW OF THERMODYNAMICS

This law states that – 
The entropy of universe is always increasing in the course of every spontaneous process.

It is impossible to construct a machine functioning in a cycle which can convert heat completely into equivalent amount of work without producing change elsewhere, i.e. perpetual motions are not allowed.

Spontaneous process 

A process which can take place either by itself or by initiation.

Non – spontaneous process

A process which can neither take place by itself nor by initiations.
The overall driving force for a process is the resultant of
(i) tendency for minimum energy and
(ii) tendency for maximum randomness.
Whenever a spontaneous process takes place, it is accompanied by an increase in the total entropy of the universe.

Example 7 : Which of the following reactions is attained to by an increase in entropy?

(A) N₂(g) + 3H₂(g)──⟶ 2NH₃(g)

(B) 2h₂(g) + O₂(g)──⟶2H₂O(ℓ)

(C) H₂(g) + I₂(g)──⟶2HL(g)

(D) C(graphite)+ H₂O(g)──⟶CO(g)+ H₂O 

Solution: (D). Increase in entropy will occur if Δn_g is positive, i.e., there is more number of gaseous products than the gaseous reactants.

Example 8 : Given that:
H₂O(ℓ,373.5 K,1 atm)──⟶H₂O(g,373.15 k,1 atm);ΔS₁
H₂O(s,273.5 K,1 atm)──⟶H₂O(ℓ,273.15 k,1 atm);ΔS₂
Predict which of the following is true
(A) ΔS₁ = S₂ (B) ΔS₁> ΔS₂
(C) ΔS₁ < S₂ (D) ΔS1may be greater or smaller than

Solution: (B). Vaporization of water creates more randomness.

Gibb’s energy

In chemical system, the substance, moves in a direction in which there is a decrease in free energy, i.e. ΔG is negative.
G = H – TS
where, G – Gibbs energy, H – Enthalpy constant, S – Entropy, T – Temperature
ΔG = ΔH ─ TΔS(Gibb’s Helmholtz equation)
Free energy change
(a) If ΔG < 0,the process is spontaneous 
(b) If ΔG > 0 the process is non – spontaneous 
(c) If ΔG = 0 the process is in equilibrium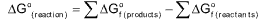

ΔG = ΔG^o + 2.203 RT log Q
where, ΔG ─ free energy change;ΔG^o ─ standard free energy change; Q – reaction quotient

Example 9 : For the reaction, 2A(g) + B(g)──⟶2D(g),
ΔU^o300k = -10.0 kJ mol^-1 and ΔS^o300k = -45J K^-1mol^-1. The reaction
(A) Will be spontaneous (B) Will not be spontaneous
(C) Will be at equilibrium (D) is endothermic

Solution: (B). ΔH^o = ΔE^o + (Δn_g)RT 
=-10.0kJ mol^-1 +(-1)(8.314 x 10^-3kJ K^-1 mol^-1)(300K)
= –12.49 kJ mol^–1 
ΔG^o = ΔH^o - TΔS^o
=-12.49 kJ mol^-1 -(300K)(-45 x 10^-3)kJ K^-1 mol^-1
= (–12.49 + 13.5) kJ mol^–1 = positive

ANSWER TO EXCERCISE

Exercise 1. C

Exercise 2. D

Exercise 3. A

Exercise 4. C

POINTS TO PONDER

1. Internal energy: It is sum of all forms of energy of all the particles present in the system at a particlar temperautre.

2. First law of thermodynamics:
ΔQ = ΔE + ΔW 

3. Enthalpy or heat constant:
H = E + PV
ΔH = ΔE + PΔV = ΔE + Δn_gRT

4. Heat capacity: It is defined as the quantity of heat required to raise the temperatuer of the system by one degree.

5. and  

6. Work done in isothermal reversible process:
W = -2.303nRTlog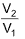
= -2.303nRTlog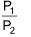 

7. Work done in adiabatic reversible expansion:
W = C_v(T₂ - T₁)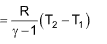

8. Adiabatic relations:
PV^γ = constant
TV^γ-1 = constant


where γ = sepecific heat ratio of gas.

9. Kirchoff’s equation
ΔH2 - ΔH1 = ΔCP(T2 - T1) (at constant pressure)
ΔE2 - ΔE1 = ΔCV(T2 - T1) (at constant volume)
 

10. Entropy: Entropy is thermodynamic quantity which is a measure of the randomness or disorders of the molecules of the system.

Spontaneous process S_(total) > 0 
Non-spontaneous processS_(total) < 0 
At equilibrium S_(total) = 0

11. Second law of thermodynamics: It states that the entropy of universe is always increasing in the course of every spontaneous process.

12. Gibb’s energy: G = H - TS

SOLVED EXAMPLES

1. Which of the following reactions correspond to the definition of enthalpy of combustion at 25oC?
(A) ΔH₁ + ΔH₂ - ΔH₃ (B) ΔH₁ - ΔH₂ + ΔH₃
(C) 2.303 x 2 x 298 log2 (D) CH₄(ℓ)+ 2O₂(ℓ)――⟶CO₂(ℓ)+ 2H₂O(ℓ)

Sol. (A). 
In enthalpy of combustion, the stoichiometric number of the species being combusted is equal to one. The products are CO₂(g) and H₂O(ℓ) when temperature is 25^oC.

2. The enthalpy of vaporization of water at 100^oC is 40.63 kJ mol^–1. Its entropy of vaporization would be
(A) 406.3 J K^–1 mol^–1 (B) 108.9 J K^–1 mol^–1
(C) 606.3 J K^–1 mol^–1 (D) 808.3 J K^–1 mol^–1

Sol. (B).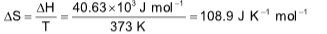 

3. For a spontaneous process at all conditions of temperature which of the following is true?
(A) ΔS positive and ΔH positive (B) ΔS positive and ΔH negative
(C) ΔS negative and ΔH positive (D) ΔS negative and ΔH negative

Sol. (B). For a spontaneous process, ΔG is negative. Since
ΔG = ΔH - TΔS
ΔG will always be negative if and only if ΔH is negative and ΔS is positive.

4. Which of the following results in a decrease in entropy?
(A) Crystallization of sucrose from solution
(B) Rusting of iron
(C) Conversion of ice into water
(D) Vaporization of camphor

Sol. (A). Decrease in disorderliness would result into the decrease in entropy.

5. If the standard free energy change for a reaction is 1.546 kJ mol^–1 at 500^oC, then the value of standard equilibrium constant for the reaction is
(A) Antilog (0.105) (B) Antilog (–0.105)
(C) Antilog (0.241) (D) Antilog (–0.241)

Sol. (B). ΔG^o = -RT In K^o 
1.546 x 103 J mol^-1 = -(8.314 J K^-1 mol^-1)(773K)In K
 
K^o =antilog(-0.105)

6. 5 mole of an ideal gas expand reversibly from a volume of 8 dm³ sp 80 dm³ at a temperature of 27°C. Calculate the change in entropy.
(A) 70.26 JK^–1 (B) 82.55 JK^–1
(C) 95.73 JK^–1  (D) 107.11 JK^–1

Sol. (C). Entropy change (ΔS) = 2.303 nR log = 2.303 x 5 x 8.314 x  = 95.73 JK^–1 

7. The molar heat capacity for a gas at constant T and P is 
(A) 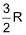(B)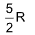  
(C) depends upon the atomicity of the gas (D) infinity 

Sol. (D).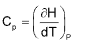
since at constant T, dT = 0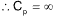

8. Given: H₂S(g) ⟶ HS(g) + H(g), ΔH^o = x₁
ΔH^o_f(H₂S,g) = x₂ and ΔH^o_f(H,g)= x₃
Hence ΔH^o_f(HS,g) is
(A) x₁ + x₂ – x₃ (B) x₃ + x₁ + x₂
(C) x₁ – x₂ – x₃ (D) x₃ – x₁ + x₂

Sol. (A). I. H₂S(g) ⟶ HS(g) + H(g), ΔH^o = x₁
II. H₂(g) + S(g)⟶ H₂S(g), ΔH^o = x₂
III.  H₂(g) ⟶ H(g) ΔHo = x₃
– – –
––––––––––––––––––––––––––––––––––––––––––––––––
I + II + III: H₂(g) + S(g) ⟶ HS(g) ΔH^o = x₁ + x₂ – x₃

9. The dissociation energy of CH4 and C2H6 to convert them into gaseous atoms are 360 and 620 kcals mol–1 respectively. The bond energy of C – C bond is
(A) 260 kcals mol–1 (B) 180 kcals mol–1
(C) 130 kcals mol–1 (D) 80 kcals mol–1

Sol. (D). S_C–H =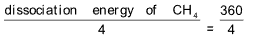
= 90 kcals mole^–1
Dissociation energy of C₂H₆ = E_C–C + 6 E_C–H
620 = E_C–C + 6 x 90
ΔE_C–C = 80 kcals mole^–1

10. Calculate the maximum efficiency of an engine operating between 110°C & 25°C.
(A) 11.1% (B) 22.2%
(C) 33.3% (D) 44.4%

Sol. (B). Maximum efficiency of an engine working between temperature T₂ & T₁ is given by
h = = 0.222% = 22.2%

ASSIGNMENT PROBLEMS

1. Change in enthalpy for the reaction
2H₂O₂(ℓ)⟶2H₂O(ℓ) + O₂(g)
If heat of formation of H₂O₂(ℓ) and H₂O(ℓ) are –188 kJ mol^–1 and –286 kJ mol^–1 respectively, is

(A) –196 kJ mol^–1

(B) +196 kJ mol^–1

(C) +948 kJ mol^–1

(D) –948 kJ mol^–1

2. In order to decompose 9g water, 142.5 kJ heat is required. Hence the enthalpy of formation of water is
(A) +285 kJ (B) –285 kJ
(C) +142.6 kJ (D) –142.5 kJ

3. Enthalpy of neutralization of HCl with NaOH is x. The heat evolved when 500 ml of 2 N HCl are mixed with 250 ml of 4 N NaOH will be
(A) 500 x (B) 100 x
(C) x (D) 10 x

4. If the bond energies of H – H, Br – Br and H – Br are 433, 192 and 364 kJ mol^–1 respectively, the ΔHo for the reaction 
H₂(g) + Br₂(g)⟶2HBr(g)is
(A) –261 kJ (B) +103 kJ
(C) +261 kJ (D) –103 kJ

5. The enthalpy of monoatomic gas at T Kelvin is

6. All the natural processes in this universe produce:
(A) a decrease in entropy of the universe
(B) an increase in entropy of the universe
(C) no change in entropy
(D) some times increase or sometimes decrease in entropy

7. ΔHf of graphite is 0.23 kJ / mole and ΔH_f for diamond is 1.896 kJ / mole. ΔH_transition from graphite to diamond is
(A) 1.66 kJ / mole (B) 2.1 kJ / mole
(C) 2.33 kJ / mole (D) 1.5 kJ / mole

8. One gram of sample of NH₄NO₃ is decomposed in a bomb calorimeter. The temperature of the calorimeter increases by 6.12 K. The heat capacity of the system is 1.23 kJ / g / deg. What is the molar heat of decomposition for NH₄NO₃?
(A) –7.53 kJ / mol (B) –398.1 kJ / mol
(C) –16.1 kJ / mol (D) –602 kJ / mol

9. Consider the reactions,
C(s) + 2H₂O ⟶ CH₄(g)₁ ΔH= -x kcal

C(g) + 4H(g)⟶ CH₄(g), ΔH= -x₁ kcal

CH₄(g) ⟶ CH₄(g), ΔH= +y kcal

The bond energy of C – H bonds is

10. Given the bond energies of N - N, H – H and N – H bonds are 945, 436 and 391 kJ/mol. respectively, the enthalpy of the reaction
N₂(g) + 3H₂(g) ⟶ 2NH₃(g) is
(A) – 93 kJ (B) 102 kJ
(C) 90 kJ (D) 105 kJ

11. Given ΔH_ioniz (HCN) = 45.2 kJ mol^–1 & ΔH_ioniz (CH₃COOH) = 2.1 kJ/mol
(A) pKa (HCN) = pKa (CH₃COOH)
(B) pKa (HCN) > pKa (CH₃COOH)
(C) pKa (HCN) < pKa (CH₃COOH)
(D) pKa (HCN) =  pKa (CH₃COOH)

12. For isothermal process which of the following is not correct?
(A) ΔE = 0
(B) ΔH = 0 
(C) In isothermal expansion,
(D) In isothermal compression,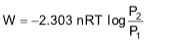 

13. Heat of hydrogenation of 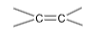 is x₁ and that of

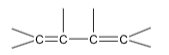is x₂, the resonance energy is equal to
(A) x₁ + x₂ (B) x₁ – x₂
(C) 2(x₁ – x₂) (D) 2x₁ – x₂

14. For the reaction,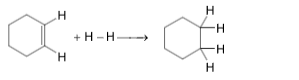

Bond energies are given as under
(i) C – C, 346 kJ / mol (ii) C – H, 413 kJ / mol
(iii) H – H, 437 kJ / mol and (iv) C = C, 611 kJ / mol

What will be the value of ΔH ,25oC for the above reaction?
(A) –289 kJ mol^–1 (B) –124 kJ mol^–1
(C) +124 kJ mol^–1 (D) +289 kJ mol^–1

15. CH₂ = CH₂(g) + H₂(g)⟶CH₃ - CH₃(g).The bond energy of C–C=80 kcal, C=C=145 kcal, C–H = 98 kcal, H–H = 103 kcal, the heat of reaction is
(A) –14 kcal (B) –28 kcal
(C) –42 kcal (D) –56 kcal

ANSWER TO ASSIGNMENT PROBLEMS

1. A 2. B 3. C

4. D 5. C 6. B

7. A 8. D 9. C

10. A 11. C 12. C

13. D 14. B 15. B