The chapter Work, Energy & Power explains energy forms, work calculation, and power in Class 9 Science. With NCERT solutions for Class 9 Science students can solve numerical problems on work done, kinetic and potential energy, and efficiency. Our class 9 notes provide clear summaries, formulas, and real-life examples to simplify learning. Class 9 science tuition makes concepts like energy transformation, work-energy theorem, and power engaging with interactive sessions. Personalized Class 9 tuitions focus on practice problems, ensuring students excel in both theoretical and numerical sections. This chapter strengthens understanding of energy conservation principles, which are fundamental for higher physics studies.
Work
Definition: Work is said to be done by a force on a body, when the force displaces the body through a certain distance in the direction of force.
Measurement of Work
The amount of work done by a body depends upon:
- The magnitude of the force
- The displacement of the body
So, by knowing the force and displacement, we can measure the work done. The amount of work done is equal to the product of the force and the displacement of the body from the point of application of the force, in the direction of force.
Work = Force × displacement of the body
Nature of quantity: Even though force and displacement are vectors, work is a scalar quantity. Work is independent of time.
Units of Work
Absolute Units:
- SI unit: joule (J)
- CGS unit: erg
Joule: The work done is said to be 1 joule, if 1 N of force displaces the body through 1 m in the direction of the force.
Erg: The work done is said to be 1 erg, if 1 dyne of force displaces the body through 1 cm in the direction of the force.
Gravitational Units:
- SI unit: kg·wt·m
- CGS unit: g·wt·cm
Relation between joule and erg:
We know that, 1 J = 1 newton × 1 m
But, 1 newton = 105 dyne and 1 metre = 102 cm
1 J = 105 dyne × 102 cm
1 J = 107 dyne·cm = 107 erg
1 erg = 1 dyne·cm
And, 1 kg·wt·m = 9.8 N·m = 9.8 J
Summary of Units
Different Expressions to Calculate the Work
(a) Work Done When Force and Displacement are in the Same Direction
Consider a body at point 'A'. It reaches the point 'B' when a force 'F' is applied, such that the displacement of the body in the direction of force is 'S'.
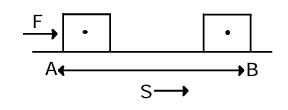
Thus, Work done (W) = Force (F) × displacement (S) in same direction
W = F × S
Note:
- The above formula should be applied only if the direction of force and displacement are the same
- The work done by a body is zero, if force is acting and displacement is zero
- As direction of displacement and direction of force are the same, work done is said to be positive
Examples of Positive Work Done:
- In villages, children are fascinated and interested to play games using marbles. In one of the games, they use their thumb and index finger to move the marble. Here, the work is done by index finger, as the force applied by it displaces the marble through some distance, in the direction of the force.
- When a shot is fired, the force of pressure of the gun powder does the work. It shifts the bullet along the barrel, with an increasing speed. In this, the direction of force and displacement of the shot are in the same direction.
- A man playing snookers with the cue.
- Cricket batsman playing straight drive.
(b) Work Done When Force and Displacement are in Opposite Direction
Consider a moving car. Try to stop the car by applying some force 'F'.
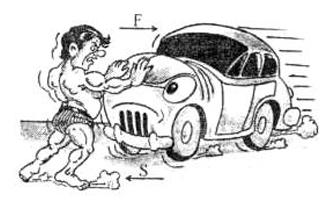
We observe that the car comes to rest after travelling some distance 'S' opposite to the direction of force. In this case, the force 'F' is applied opposite to the direction of the motion or displacement of the car. Therefore, the displacement is taken as '−S'.
Thus, Work done = Force acting × Displacement in opposite direction
W = F × (−S) = −FS
Note: As direction of displacement and direction of force are opposite to each other, work done is said to be negative.
Examples of Negative Work Done:
- A man moving upwards on the stairs.
- Applying brakes of a moving motor vehicle.
- Rowing a boat on the surface of the water.
- An elevator moving upwards in a building. [Force acting upward]
(c) Work Done by a Force That Makes an Angle with the Direction of Displacement
We have seen that whenever work is done, a body displaces in the same direction or in opposite direction of the force applied.
But, in some cases, the body moves in a direction that makes an angle with the direction of the applied force.
For example, when a child pulls a toy car, using a string attached to it, the car moves horizontally on the ground, but the force applied by the child is along the string held in his hand, making an angle with the direction of the displacement of the body which is horizontal to the surface of the ground.
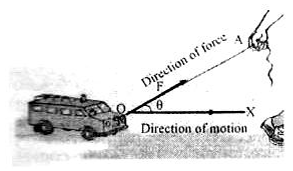
The toy moves along the horizontal ground surface 'OX', but, the force is along the string 'OA'. Thus, the direction of force makes an angle 'θ' with the direction of the motion. In such cases, we cannot use the formula W = F × S
To calculate the work done, as the displacement 'S', is not exactly in the direction of the force applied. Therefore, we need to know the magnitude of force in the direction of motion of the body.
Let us try to find the magnitude of force (F) that acts horizontally. As force is a vector quantity and makes some angle with the horizontal, it can be resolved into two components (parts):
- Horizontal component (FH): One component along the direction in which the body moves, called horizontal component of force.
- Vertical component (Fv): The other component acting perpendicular to the horizontal i.e., vertically upwards called vertical component. The vertical component tries to lift the body, but does not actually lift it. Therefore, the vertical component does no work, as there is no displacement vertically upwards.
The work is done only by the horizontal component of force FH, as the body moves in horizontal direction.

FH can be expressed in terms of F and θ as follows:
From the figure,
Cos θ = Adjacent side/Hypotenuse = OX/OA = FH/F
Cos θ = FH/F ⇒ FH = F Cos θ
Here, work done is measured as product of magnitude of component of force, along the direction of displacement and magnitude of displacement.
Thus, Work = Magnitude of component of force × displacement of the body
= F Cos θ × S = FS Cos θ
Work done W = FS Cos θ
Note:
- Cos 0° = 1, Cos 30° = √3/2, Cos 45° = 1/√2
- Cos 60° = 1/2 and Cos 90° = 0
(d) Work Done Against Gravity
Consider a book or an object lifted from a table, we do work against the force of gravity.
Whenever work is done against gravity, the force required to lift the body is equal to its weight. Therefore, the amount of work done is equal to the product of weight of the body and the vertical distance through which the body is lifted.
Suppose a body of mass 'm' is lifted vertically upwards through a distance 'h', then the force required to lift the body will be equal to the weight of the body, m × g, where 'g' is acceleration due to gravity.
Work done by the person in lifting a body = weight of the body × vertical distance.
W = m × g × h
When work is done against gravity, W = −mgh
Note: When work is done against gravity 'acceleration due to gravity is taken as g'. The magnitude of work is always positive.
Example of Work Done Against Gravity:
When a suitcase is lifted from the ground to some height, work is done against gravity.

Some Examples of Zero Work
Person pushing a wall: Consider a person standing in front of a wall, trying to push it. He is unable to move it. Here, displacement of the wall is zero. Hence, no work is done by him.

Coolie standing with load: A coolie standing with a heavy load on his head does no work, although he feels tired, as his displacement is zero.

Work done by the Sun to move the Earth: In the case of the Earth revolving round the Sun, the direction of the force and the direction of displacement is such that the angle θ = 90°
We know, when force makes an angle with displacement, work done is W = FS Cos θ. Substituting θ = 90°
We get, W = F × S × Cos 90°
As Cos 90° = 0 ⇒ W = F × S × 0 ⇒ W = 0
Therefore, work done by the Sun to move the Earth is zero.
- Work done by a porter to carry load: In this case of a porter carrying a load and moving, the direction of force (weight of the load) and displacement are perpendicular to each other.
Observe that θ = 90°
We know that when force makes an angle with displacement, work done is W = Fs Cos θ = FS Cos 90°
Substituting Cos 90° = 0
We get, W = F × S × 0 ⇒ W = 0
From the above examples, we can conclude that, the work is said to be zero:
- If the force alone acts and there is no displacement.
- If both force and displacement are perpendicular to each other.
Solved Examples
Question: A body at rest has mass 10 kg. It is moved by a horizontal force of 5 N on a horizontal surface. Calculate the work done by the force in 8 s.
Solution:
Given:
- Mass of the body (m) = 10 kg
- Force (F) = 5 N
- Time (t) = 8 s
- Work done (W) = ?
From equation of motion, S = ut + ½at²
⇒ S = ½at² (∵ u = 0)
How to get 'a'? From relation, F = ma
We have, a = F/m = 5/10 = 0.5 m/s²
We get, S = ½ × 0.5 × (8)² = 16 ⇒ S = 16 m
From formula, W = F × S
We get, W = 5 × 16 = 80
The work done by the force in 8s is 80 J.
Question: If a servant lifts 10 m³ of liquid from a tank, which is at a depth of 40 m. If the work done by him is 1600 J, then find the density of the liquid (take g = 10 ms⁻²).
Solution:
Given:
- Volume of liquid (V) = 10 m³
- Depth of tank (h) = 40 m
- Acceleration due to gravity (g) = 10 ms⁻²
- Work done (W) = 1600 J
- Density of liquid (d) = ?
We know, W = mgh
⇒ W = V × d × g × h [But, mass (m) = Volume (V) × Density (d)]
d = W/(V × g × h)
d = 1600/(10 × 10 × 40) = 0.4 kg/m³
Therefore, the density of the liquid is 0.4 kg/m³
Question: A car weighing 1000 kg and travelling at 30 m/s stops at a distance of 50 m, retarding uniformly. What is the force exerted on it by the brakes? What is the work done by the brakes?
Solution:
Given:
- Mass (m) = 1000 kg
- Initial velocity (u) = 30 m/s
- Final velocity (v) = 0 m/s
- Displacement (S) = 50 m
- (i) Force F = ?
- (ii) Work done W = ?
(i) Finding Force:
We know, F = ma
How to get a?
From equation, v² − u² = 2aS
⇒ a = (v² − u²)/(2S) = (0² − 30²)/(2 × 50) = −900/100 = −9 ms⁻²
Substituting the above value in F = ma,
We get F = 1000 × −9 = −9000 N
(−ve sign indicates that the force is retarding)
The retarding force is 9000 N.
(ii) Finding Work:
We know, W = F × S = −9000 × 50 = −4,50,000 joule
(−ve sign indicates that the work is done with retarding force)
∴ The negative work done is 4,50,000 joule
Power
Power is the rate at which work is done.
Measurement of Power
The amount of power of a body depends upon:
- The magnitude of the work
- The time taken by the body
So, by knowing the work and time, we can measure the power. The amount of power is the ratio of work and time.
Power = Work/Time
Units of Power
(i) CGS unit:
We know that,
Power (P) = Work done (W) / Time taken (t)
CGS unit of power = CGS unit of work / CGS unit of time
⇒ CGS unit of power = erg/second
(ii) SI unit:
We know that,
Power (P) = Work done (W) / Time taken (t)
SI unit of Power = SI unit of work / SI unit of time
⇒ SI unit of power = joule (J) / second (s) = J/s = JS⁻¹
The ratio joule/second is called watt (W).
Watt: If 1 joule of work is done in 1 second, then the power is said to be 1 watt
1 watt = 1 joule / 1 second
(iii) Bigger units of power:
The bigger units of power are kW and MW.
- 1 kilowatt (kW) = 1000 W
- 1 Megawatt (MW) = 10⁶ W
(iv) Practical unit of power:
The widely used practical unit of power is Horse-power (hp)
1 hp = 746 W = 0.746 kW
Horsepower: Horsepower is defined as work done over time. The exact definition of one horsepower is 33,000 lb·ft/minute. Put another way, if you were to lift 33,000 pounds to a height of one foot over a period of one minute, you would have been working at the rate of one horsepower.
Different Expressions of Calculating Power
(i) Power to Move a Body
Consider a force 'F' acting on a body that is displaced in the direction of force by a distance 'S'.
Then the power is given by the following expression:
Power (P) = Work done (W) / Time (t) = [Force (F) × displacement (S)] / Time (t)
P = FS/t
(ii) Power to Stop a Moving Body
Consider a force 'F' acting on a body against the direction of the motion of the body. The body is stopped in time 't' after travelling through a distance 'S'.
Then, the power used to stop the body can be obtained by the following expression:
Power (P) = Work done (W) / Time (t) = [Force (F) × displacement (S)] / Time (t)
P = −FS/t
Note: −ve sign indicates that power is used against the direction of motion of the body.
(iii) Power to Pull a Body
Consider a force 'F' acting in the direction that makes an angle 'θ' with the direction of the motion.
If 'S' is the distance travelled by the body in time (t), then power used by the body can be calculated by the following expression:
Power (P) = Work done (W) / Time (t)
Power = (FS Cos θ)/t
(iv) Power to Lift a Body Against Gravity
Consider a mass 'm' lifted from the surface to a height 'h' against gravity. If 't' is the time taken to lift the body, then the power can be calculated by the following expression:
Power (P) = Work done (W) / Time (t)
= [Weight of the body (mg) × Distance through it is filled (h)] / Time (t)
Power = mgh/t
Power against gravity, P = −mgh/t
(v) Power of a Body Moving with Velocity (v)
Consider a body moving with a speed or velocity of 'v' m/s. If 'F' is the force applied to stop the body, then the power of body is given by the following expression:
Power (P) = Work done (W) / Time (t) = [Force (F) × Displacement (S)] / Time (t)
⇒ P = FS/t ⇒ P = F × (S/t) (∵ v = S/t)
P = F × v
Solved Examples
Question: A body does 20 J of work in 5 s. What is its power?
Solution:
Given:
- Work done by a body (W) = 20 J
- Time (t) = 5 s
- Power (P) = ?
Selection of Formula: Power (P) = Work/Time = W/t = 20/5 = 4
⇒ P = 4 Js⁻¹
The power of a body is 4 Js⁻¹ or 4 W.
Question: If an engine lifts 4000 m³ of water from a depth of 500 m in 40 minutes, then calculate (i) Work done by the motor and (ii) Power of the motor. [Hint: g = 10 m/s², density of water = 10³ kg/m³]
Solution:
Given:
- Volume of water (V) = 4000 m³
- Density of water (d) = 1000 kg/m³
- Height (h) = 500 m
Mass of water (m) = V × d = 4000 m³ × 10³ kg/m³ = 4 × 10⁶ kg
(i) Work done in lifting water:
= P.E. = mgh
= 4 × 10⁶ × 10 × 500 = 2 × 10¹⁰ J
(ii) Power of the motor:
= W/t = (2 × 10¹⁰)/(40 × 60) = (2 × 10¹⁰)/2400
= (1 × 10¹⁰)/1200 = (1/12) × 10⁸ = 0.83 × 10⁷ W
Question: What is the power of pump which takes 10s to lift 100 kg of water to a water tank situated at a height of 20 M? (g = 10 m/s²)
Solution:
Given:
- Time (t) = 10 s
- Mass (m) = 100 kg
- Height (h) = 20 m
- Acceleration due to gravity (g) = 10 m/s²
- Power (P) = ?
Selection of Formula: Power (P) = Work done (W) / Time (t)
How to get W?
We know, work done in lifting a body against gravity, W = mgh = 100 × 10 × 20 = 20000 J
∴ P = 20000/10 = 2000 W
The power developed is 2000 W.
Question: An engine lifting water from a well of depth 30 m fills a tank of size 2m × 2m × 2m with water in 5 minutes. Find the power of the engine? (g = 10 ms⁻²)
Solution:
Given:
- Volume (V) = 2 × 2 × 2 = 8 m³
- Acceleration due to gravity (g) = 10 m/s²
- Time (t) = 5 min = 5 × 60 = 300 s
- Height (h) = 30 m
- Power (P) = ?
Selection of Formula: Power (P) = Work done (W) / Time (t)
How to get W?
We know, work done in lifting a body against gravity, W = mgh
∴ P = mgh/t ---------(1)
How to get m?
We know, m = V × d, where V is volume and 'd' is density of water (10³ kg/m³)
∴ m = 8 × 1000 = 8000 kg
Substituting the values in (1), we get
P = (8000 × 10 × 30)/300 = 8000 W
Question: A man carries a load of 50 kg through a height of 40 m in 25s. If the power of the man is 1569 W, then find his mass? (Take g = 10 ms⁻²)
Solution:
Given:
- Mass of the load (m₁) = 50 kg
- Height (h) = 40 m
- Time (t) = 25 s
- Power (P) = 1568 W
- Acceleration due to gravity (g) = 10 m/s²
- Mass of the man (mₘ) = ?
Selection of formula: Power (P) = Work done (W) / Time (t)
How to get W?
We know, work done in lifting a body against gravity, W = mgh
∴ P = mgh/t
Here, m = m₁ + mₘ
∴ P = (m₁ + mₘ)gh/t ----------(1)
Substituting the value in (1), we get
1568 = [(50 + mₘ) × 10 × 40]/25
mₘ + 50 = 1568 × (25/400) ⇒ mₘ + 50 = 98
⇒ mₘ = 98 − 50 = 48 kg
Therefore, the mass of man is 48 kg
Energy
Energy can be defined as the capacity to do work.
Let us take an example, for our better understanding. A stone cutter raises his hammer vertically above the stone and then hits it to break into small pieces. In doing so he does some work in raising the hammer. If the hammer is allowed to fall on the stone, it can do work in breaking the stone.
Thus, the work done in raising the hammer has been stored up in it, giving in the ability of doing work. Now, when the hammer is resting on the stone, it can no longer do any work.
Thus, we can say that the raised hammer has the energy or ability to do work. The amount of energy possessed by a body is equal to the amount of work it can do when its energy is released.
Measuring Formula for Energy
As energy is the capacity to do work, its measuring formula is same as that of the work done.
Energy of a body (E) = Work done (W) of the same body
Units:
- SI unit: joule
- CGS unit: erg
Note: Energy is the capacity to do work. Hence, its units are same as that of work.
Electrical Unit of Energy - Kilowatt-hour (kWH)
As we know, electric energy is required to run the lamps and all the electric appliances i.e., refrigerators, heaters, televisions etc. The electric bill which we get monthly is always in terms of units.
Ex: If our electricity bill shows 50 units, it means the electrical appliances of our house had consumed 50 kW.
∴ 1 unit = 1 kWH
Thus, kWH is the amount of electric energy used by 1000 W electrical appliances, when they operate for 1 hour.
∴ 1 kWH = 1000 WH
Relation between kWH and Joules:
1 kWH = 1000 WH ----------(1) (∵ 1 kW = 1000 W)
As we know that, 1W = 1 Js⁻¹ and 1 hour = 60 × 60 s = 3600 s
Substitute the above values in (1), we have
1 kWH = 1000 WH = 1000 × 1 Js⁻¹ × 3600 s
= 3.6 × 10⁶ J
1 kWH = 3.6 × 10⁶ J
Kinetic Energy
Kinetic energy can be defined as energy possessed by an object by virtue of its motion.
Examples of Kinetic Energy:
- Energy possessed by a moving bicycle
- Energy possessed by running water of a river
- Energy possessed by a shooting arrow
- Energy possessed by blowing wind
- Energy possessed by a swimming fish in water
- Energy possessed by a spinning electron round the nucleus
Types of Kinetic Energy
There are three types of kinetic energy. They are:
- Vibrational energy
- Rotational energy
- Translational energy
Factors Affecting Kinetic Energy
(i) Kinetic Energy and Mass:
Suppose a tennis ball and an iron ball are thrown towards you with the same velocity. Which one is easier to catch? It is obvious that the tennis ball is easier to catch as it has less impact on the hand compared to an iron ball. This implies that kinetic energy possessed by a tennis ball is less than that of an iron ball.
Conclusion: Kinetic energy of a body depends on its mass
The more the mass of a body, the greater its kinetic energy
(ii) Kinetic Energy and Velocity:
Consider the case of two stones A and B of same mass hitting a glass window. Let the velocity of 'A' (vA) be greater than the velocity of 'B' (vB) i.e., vA > vB. Then, the impact of the stone 'A' would be much greater than the impact of 'B' on a glass window. This implies that Kinetic energy possessed by 'B' is less than that of 'A'. An object moving faster possesses more kinetic energy than an object moving slower.
Conclusion: Kinetic energy of body depends on the velocity of a body.
Mathematical Expression for K.E.
Consider a body of mass 'm' at rest. When a force is applied, it sets into motion and acquires a velocity after travelling a distance of 'S'.
Force = ma, where 'a' is the acceleration of the body. In this case, kinetic energy is measured by the amount of work done by the force to acquire the velocity.
⇒ K.E. = Force × Displacement = ma × S ----------(1)
We know, v² − u² = 2aS ⇒ a = (v² − u²)/(2S)
Substituting the above value in (1), we get
Kinetic energy = m × [(v² − 0²)/(2S)] × S
K.E. = mv²/2 or (1/2)mv²
Kinetic energy = (1/2) × mass × (velocity)²
Thus, the kinetic energy of the body is equal to half of the product of its mass and square of the velocity of the body.
We see that kinetic energy of a body is directly proportional to the square of the velocity and mass of the body.
- K.E. ∝ mass of the body
⇒ Larger the mass of the body, greater its K.E. - Also K.E. ∝ v²
⇒ If velocity of a body is doubled, then its K.E. also gets increased by four times.
Relation Between Momentum and Kinetic Energy
Consider a body of mass 'm' moving with velocity 'v'.
We know, Momentum = mass × velocity ⇒ p = m × v ----------(1)
Kinetic energy = (1/2) × mass × velocity²
⇒ K.E. = (1/2) m × v² ----------(2)
On multiplying and dividing by 'm' in the R.H.S. of eq (2), we get
K.E. = (m² × v²)/(2m) = (mv)²/(2m)
But, from equation (1), p = mv
∴ K.E. = p²/(2m)
Relation Between Work Done and Kinetic Energy
Let a body of mass 'm' move with a velocity 'u' m/s. Let a force (F) act on it in the direction of motion. This increases the velocity of the body to 'v' m/s.
Let the displacement of the body be 'S' m
Selection of the formula: v² − u² = 2aS
⇒ a = (v² − u²)/(2S)
Let us now calculate the force acting on the body.
Force = mass × acceleration = m × [(v² − u²)/(2S)]
We know work done, W = force × displacement
= m × [(v² − u²)/(2S)] × S = m × [(v² − u²)/2]
= mv²/2 − mu²/2 = Final K.E. − initial K.E.
= increase or change in K.E.
Thus, we conclude that 'work done on a moving body is equal to the change in its kinetic energy.' This is known as work energy theorem.
SOLVED EXAMPLES
Question: Calculate the kinetic energy of a body of mass 2 kg moving with a velocity of 0.1 m/s.
Solution:
Given:
- Mass of body (m) = 2 kg
- Velocity of the body (v) = 0.1 m/s
- Kinetic energy (K.E) = ?
Selection of Formula: K.E. = (1/2)mv²
= (1/2) × 2 × (0.1)² = 0.01 joule
The K.E. of the body is 1 × 10⁻² J
Question: When the mass and velocity of the body are doubled, what happens to its kinetic energy?
Solution:
Let the mass, initial velocity and K.E. of the body be m, v and K respectively.
| Case-I | Case-II |
|---|---|
| Mass of body (m₁) = m | doubled mass of the body (m₂) = 2m |
| Velocity (v₁) = v | doubled velocity of the body (v₂) = 2v |
| Kinetic energy (K.E₁) = K | Kinetic Energy (K.E₂) = ? |
Selection of Formula: K.E. = (1/2)mv²
Apply the formula to both the cases.
K.E₁ = K = (1/2)mv² ------(1)
K.E₂ = (1/2)m₂V₂² = (1/2) × 2m × (2v)² = 4mv² ------(2)
Dividing (2) by (1), we get
K.E₂/K.E₁ = 4mv²/[(1/2)mv²] = K.E₂/K = 8 ⇒ K.E₂ = 8K
When the mass and velocity of the body are doubled, the kinetic energy becomes 8 times the original.
Question: A body is moving in a straight line with a certain velocity. Another body with double the mass and half the velocity of the first, is moving in the straight line. What is the ratio of kinetic energy of 2nd body with the first body?
Solution:
| Case-I (first body) | Case-2 (Second body) |
|---|---|
| Mass of the first body (m₁) = m | Mass of second body (m₂) = 2m |
| Velocity of the first body (v₁) = v | velocity of second body (V₂) = V₁/2 = V/2 |
| Kinetic energy of the first body (K.E)₁ = ? | Kinetic Energy (K.E)₂ = ? |
We know, K.E. = (1/2)mv²
Applying the above formula to both the cases, we get
KE₁ = (1/2)mv² ---------(1)
KE₂ = (1/2) × 2m × (v/2)² = (1/2)mv² × (1/2) ---------(2)
Dividing (2) by (1), we get
(K.E)₂/(K.E)₁ = [(1/2)mv² × (1/2)]/[(1/2)mv²] = 1/2
The ratio of K.E. of the second body to first body is 1:2
Question: If the velocity of a body is tripled, then find the % of change in K.E.
Solution:
| Case-I (Initial) | Case-II (Final) |
|---|---|
| Mass of the first body (m₁) = 'm' kg | Mass of the second body (m₂) = 'm' kg |
| Velocity of first body (v₁) = 'v' m/s | Velocity of second body (v₂) = 3v m/s |
| K.E₁ = ? | K.E₂ = ? |
Selection of Formula: K.E. = (1/2)mv²
Applying the above formula to both cases, we get
Initial kinetic energy, (K.E.)₁ = (1/2)mv²
Final kinetic energy (K.E.)₂ = (1/2)m(3v)² = (9/2)mv²
Percentage of change in K.E. = ?
Percentage of change in K.E. = [(Final K.E. - Initial K.E.)/Initial K.E.] × 100
= [[(9/2)mv² − (1/2)mv²]/[(1/2)mv²]] × 100
= [[9mv² − mv²]/2]/[mv²/2] × 100
= [mv²/mv²] × 100 = 800
Therefore, the % change in K.E. is 800
Question: If the mass of a body is changed to 16 times, then what should be the change in velocity, such that its K.E. remains same?
Solution:
Let 'm' and 'v' be the initial mass and initial velocity of the body
| Case-I | Case-II |
|---|---|
| Initial mass of body (m₁) = m | Final mass of the body (m₂) = 16m |
| Initial velocity (v₁) = v | Final velocity (v₂) = ? |
Initial kinetic energy (K.E) = (1/2)m₁v₁²
Given, initial K.E. = final K.E.
(1/2)mv² = (1/2) × 16m × v₂² ⇒ v₂² = v²/16
⇒ v₂ = v/4
To keep the kinetic energy constant, the velocity of the body should be changed to v/4.
Question: Two bodies of masses m₁ and m₂ are moving with equal kinetic energies. What is the ratio of their momentum?
Solution:
Let p₁ and p₂ be the momentum of first and second respectively
| Case-I (first body) | Case-2 (second body) |
|---|---|
| Mass of first body (m₁) = m₁ | Mass of second body (m₂) = m₂ |
| Momentum of first body = p₁ | Momentum of second body = p₂ |
Ratio of their momentum = p₁/p₂ = ?
The main terms in data are kinetic energy and momentum
The formula connecting them is K.E. = p²/(2m) ⇒ p = √(2mKE)
p ∝ √m (∵ K.E. is same in both the cases)
p₁/p₂ = √(m₁/m₂)
Therefore, the ratio of their momentum is m₁ : m₂
Question: Two bodies of mass m₁ and m₂ are moving with equal momentum. What is the ratio of their kinetic energies?
Solution:
Let E₁ and E₂ be the kinetic energies of first and second body respectively.
| Case-I (first body) | Case-2 (Second body) |
|---|---|
| Mass of first body (m₁) = m₁ | Mass of second body (m₂) = m₂ |
| Momentum of first body = p | Momentum of second body = p |
The terms in data are, kinetic energy, momentum and mass
Selection of formula: K.E = p²/(2m)
⇒ KE ∝ 1/m (∵ momentum and 1/2 are constants)
(K.E.)₁/(K.E.)₂ = m₂/m₁ or E₁/E₂ = m₂/m₁
Therefore, the ratio of their kinetic energies is m₂ : m₁
Question: When the momentum of a body is doubled, how does its kinetic energy change?
Solution:
Let m, p and E be the mass, initial momentum and kinetic energy of the body respectively.
| Case-I | Case-2 |
|---|---|
| Initial momentum (p₁) = p | Final momentum (p₂) = 2p |
| Mass of the body (m₁) = m | Mass of the body (m₂) = m |
| Initial Kinetic energy (K.E.)₁ = E | Final kinetic energy (K.E.)₂ = ? |
Selection of Formula: K.E. = p²/(2m)
Applying the above formula in both the cases, we get
(K.E.)₁ = E = p₁²/(2m₁) = p²/(2m) ------(1)
(K.E.)₂ = p₂²/(2m₂) = (2p)²/(2m) = 4p²/(2m) ------(2)
Dividing (2) by (1), we get
(K.E.)₂/(K.E.)₁ = [4p²/(2m)]/[p²/(2m)] = 4 ⇒ (K.E.)₂ = 4(K.E.)₁
Therefore, the final kinetic energy becomes 4 times the initial kinetic energy.
POTENTIAL ENERGY
Definition: Potential energy can now be defined as "energy possessed by a body by virtue of its state, shape or position"
Examples of Potential Energy:
- The energy possessed by a stretched bow or by a stretched string
- The energy possessed by water, stored high up in the dams
Factors Affecting Potential Energy
(i) Potential Energy and Mass:
Suppose a tennis ball and an iron ball of same volume are dropped from same height on to a glass plate placed on the surface of the ground. Which one creates more impact on glass surface and breaks it into piece? It is obvious that the iron ball has more impact on glass surface and breaks the glass into piece.
This implies that potential energy possessed by an iron ball is more than that of tennis ball.
Conclusion: Thus, potential energy of a body depends on its mass. The more the mass of the body, the more its potential energy.
(ii) Potential Energy and Height:
Consider two cricket balls of same mass dropped from two different heights - 'h' and '2h' respectively. Which one is easier to catch and creates less impact on hands? The one dropped from a height 'h' is easier to catch and creates less impact on hands than the one dropped from height '2h'. This implies that potential energy of ball dropped from '2h' is more compared to that dropped from 'h'.
Conclusion: Potential energy of a body depends on the height at which the body is present. The more the height at which the body is present, the more its potential energy.
(iii) Potential Energy and Place:
Assume two bodies of same mass are allowed to drop from some height. But one is on the surface of the earth and the other on the surface of the moon. Which one will hit the ground with more velocity and creates more impact?
Let us find.....
The impact created depends on the velocity with which the bodies hit the ground
We know that, v² − u² = 2gh
⇒ v² = 2gh (∵ Initial velocity, u of a freely falling body is zero)
∴ v = √(2gh) (or) v ∝ √g (∵ 'h' is same in both cases)
From the above equation, it is clear that 'v' is more if 'g' is more and 'g' on the earth is 6 times that on the moon. Hence, the body falling on the surface of the earth creates more impact on the ground as 'g' is more on the earth.
Conclusion: Thus, Potential energy depends on acceleration due to gravity. The more the acceleration due to gravity of a place, the more the potential energy experienced by a body.
Mathematical Expression for Potential Energy
Consider a body of mass 'm' lifted to a height 'h', against gravity from a point A to a point B.
Force required to lift the body 'F' = weight of the body
⇒ F = m × g ---------(1)
As distance moved by the body 'S' = h
Work done (W) = F × S = mg × h [using (1)]
∴ W = mgh ---------(2)
This work done is stored in the form of energy, called "Potential energy"
∴ W = P.E. = mgh
Therefore, Potential energy = mgh
Note:
- The potential energy of a body lying on the surface of earth is taken as zero.
- The potential energy of the body decreases as it falls towards the surface of the earth
- The potential energy of the body increases as the height of the body from the surface of the earth increases.
Different Types of Potential Energies
There are two types of potential energies. They are:
- Gravitational potential energy
- Elastic potential energy
(i) Gravitational Potential Energy:
Consider a stone lifted to the roof of a house. Some work is done in lifting the stone against the gravity and this is stored in the form of potential energy. Here, the energy is stored by doing work against gravity. Hence, this type of energy is called Gravitational potential energy.
Factors affecting gravitational potential energy are:
- mass of the object
- the height to which it is raised and
- gravitational pull (acceleration due to gravity)
(ii) Elastic Potential Energy:
Consider an archer who is stretching the string of his bow. When the string is released the arrow hits the target. Here, some work is done in stretching the string.