Principle (why it’s a “clock”) In a common school-lab version, hydrogen peroxide oxidizes iodide to iodine in acidic medium. A fixed, small charge of thiosulfate “hides” the generated iodine by reducing it back to iodide. Once thiosulfate is exhausted, free iodine instantly forms a deep-blue complex with starch. Because the blue color appears only after a fixed threshold of I 2 has formed, the time to blue ( t* ) is inversely related to the initial rate of iodine production. Key reactions (H 2 O 2 /I − /H + variant) H2O2 + 2 I− + 2 H+ → I2 + 2 H2OI2 + 2 S2O3^2− → 2 I− + S4O6^2−I2 + starch → deep-blue complex (endpoint) Chemicals & setup Solution A: KI (iodide), acid (e.g., H 2 SO 4 ), starch indicator, and a fixed small amount of Na 2 S 2 O 3 . Solution B: H 2 O 2 (varied concentration to probe order). Volumetric pipettes, beakers, stopwatch, water bath (for temperature studies), white tile for endpoint clarity, PPE. Procedure (comparative runs) Keep total volume, ionic strength, and temperature constant across runs. Hold the initial thiosulfate amount fixed in every run (sets a constant I 2 threshold). Vary one reactant concentration at a time (e.g., [H 2 O 2 ]) to isolate its effect on rate. Mix A + B quickly, start the stopwatch, swirl gently, and record t* when blue appears. Repeat trials for each condition; average times to reduce random error. For temperature dependence, equilibrate both solutions at the target °C before mixing. Data analysis & calculations When the initial thiosulfate charge (threshold) is identical across runs and the total volume is constant, the initial rate is proportional to 1/ t* . Hence, if you change only one concentration between two runs, you can estimate the corresponding partial order by taking ratios. Order in H 2 O 2 (example): rate &prop; 1/t* &prop; [H2O2]^mm ≈ ln(t*1/t*2) / ln([H2O2]2/[H2O2]1) Obtain orders in iodide and acid similarly. With orders in hand, compute k from any run using the empirical rate law. For temperature dependence, build an Arrhenius plot by computing a pseudo-order k at each T and plotting ln k vs 1/T to estimate E a (slope = − E a /R). Worked mini-example Run 1: [H2O2]1 = 0.10 M, t*1 = 52 sRun 2: [H2O2]2 = 0.20 M, t*2 = 26 st*1/t*2 = 2.00; [H2O2]2/[H2O2]1 = 2.00 ⇒ m = ln 2 / ln 2 = 1 Quality & safety Wear PPE; concentrated H 2 O 2 is an oxidizer. Use fresh starch; aged starch delays the endpoint. Assign one person to timing to avoid reaction-time variability. Rinse acid spills with plenty of water; neutralize as per lab protocol. Exam-ready tips State the mechanism, define the clock threshold, justify rate &prop; 1/t*. Show log-ratio math to extract partial orders succinctly. Include one tidy Arrhenius calculation when temperature data are given.

Principle (why it’s a “clock”) In a common school-lab version, hydrogen peroxide oxidizes iodide to iodine in acidic medium. A fixed, small charge of thiosulfate “hides” the generated iodine by reducing it back to iodide. Once thiosulfate is exhausted, free iodine instantly forms a deep-blue complex with starch. Because the blue color appears only after a fixed threshold of I 2 has formed, the time to blue ( t* ) is inversely related to the initial rate of iodine production. Key reactions (H 2 O 2 /I − /H + variant) H2O2 + 2 I− + 2 H+ → I2 + 2 H2OI2 + 2 S2O3^2− → 2 I− + S4O6^2−I2 + starch → deep-blue complex (endpoint) Chemicals & setup Solution A: KI (iodide), acid (e.g., H 2 SO 4 ), starch indicator, and a fixed small amount of Na 2 S 2 O 3 . Solution B: H 2 O 2 (varied concentration to probe order). Volumetric pipettes, beakers, stopwatch, water bath (for temperature studies), white tile for endpoint clarity, PPE. Procedure (comparative runs) Keep total volume, ionic strength, and temperature constant across runs. Hold the initial thiosulfate amount fixed in every run (sets a constant I 2 threshold). Vary one reactant concentration at a time (e.g., [H 2 O 2 ]) to isolate its effect on rate. Mix A + B quickly, start the stopwatch, swirl gently, and record t* when blue appears. Repeat trials for each condition; average times to reduce random error. For temperature dependence, equilibrate both solutions at the target °C before mixing. Data analysis & calculations When the initial thiosulfate charge (threshold) is identical across runs and the total volume is constant, the initial rate is proportional to 1/ t* . Hence, if you change only one concentration between two runs, you can estimate the corresponding partial order by taking ratios. Order in H 2 O 2 (example): rate &prop; 1/t* &prop; [H2O2]^mm ≈ ln(t*1/t*2) / ln([H2O2]2/[H2O2]1) Obtain orders in iodide and acid similarly. With orders in hand, compute k from any run using the empirical rate law. For temperature dependence, build an Arrhenius plot by computing a pseudo-order k at each T and plotting ln k vs 1/T to estimate E a (slope = − E a /R). Worked mini-example Run 1: [H2O2]1 = 0.10 M, t*1 = 52 sRun 2: [H2O2]2 = 0.20 M, t*2 = 26 st*1/t*2 = 2.00; [H2O2]2/[H2O2]1 = 2.00 ⇒ m = ln 2 / ln 2 = 1 Quality & safety Wear PPE; concentrated H 2 O 2 is an oxidizer. Use fresh starch; aged starch delays the endpoint. Assign one person to timing to avoid reaction-time variability. Rinse acid spills with plenty of water; neutralize as per lab protocol. Exam-ready tips State the mechanism, define the clock threshold, justify rate &prop; 1/t*. Show log-ratio math to extract partial orders succinctly. Include one tidy Arrhenius calculation when temperature data are given.

Recurring patterns (with prep cues) First-order decay: Compute k, t 1/2 , fraction remaining, or time; read slopes from ln[A] vs t . Prep: practice two-point forms and fast half-life ladders. Zero-order linear drop: Half-life depends on [A]_0 ; completion time matters. Prep: visualize the line hitting zero; never report negative concentrations. Second-order inverse concentration: Use [A]_t=[A]_0/(1+k[A]_0 t) ; linearity of 1/[A] vs t . Prep: drill unit patterns (M⁻¹·time⁻¹). Arrhenius two-point: Find E a , predict k, or temperature for doubling. Prep: Kelvin only; align energy units; guard the sign in (1/T_2-1/T_1) . Order from data: Initial-rates log-ratios; integrated-plot linearity checks; clock reaction ratios. Prep: 60-second routine to identify what changed and compute the minimal ratio. Conceptual one-liners: order vs molecularity, catalyst effects, pseudo-first order, zero-order saturation. Prep: 2–3 sentence cards for rapid recall. Mixed context problems: Combine Arrhenius with half-life or order detection before computation. Prep: solve 5–6 compound items where model selection is step one. Training stack & exam execution Daily pattern drill: 5 first-order, 3 zero-order, 3 second-order, 3 Arrhenius, 2 order-from-data. Weekly mini-mock: 35–40 mixed Q under time pressure; log errors and re-solve within 24 hours. Triage on exam day: Attempt your strongest patterns first (often first-order & Arrhenius), then data-heavy items. Method marks: Write the formula before numbers; carry units through every line.

Recurring patterns (with prep cues) First-order decay: Compute k, t 1/2 , fraction remaining, or time; read slopes from ln[A] vs t . Prep: practice two-point forms and fast half-life ladders. Zero-order linear drop: Half-life depends on [A]_0 ; completion time matters. Prep: visualize the line hitting zero; never report negative concentrations. Second-order inverse concentration: Use [A]_t=[A]_0/(1+k[A]_0 t) ; linearity of 1/[A] vs t . Prep: drill unit patterns (M⁻¹·time⁻¹). Arrhenius two-point: Find E a , predict k, or temperature for doubling. Prep: Kelvin only; align energy units; guard the sign in (1/T_2-1/T_1) . Order from data: Initial-rates log-ratios; integrated-plot linearity checks; clock reaction ratios. Prep: 60-second routine to identify what changed and compute the minimal ratio. Conceptual one-liners: order vs molecularity, catalyst effects, pseudo-first order, zero-order saturation. Prep: 2–3 sentence cards for rapid recall. Mixed context problems: Combine Arrhenius with half-life or order detection before computation. Prep: solve 5–6 compound items where model selection is step one. Training stack & exam execution Daily pattern drill: 5 first-order, 3 zero-order, 3 second-order, 3 Arrhenius, 2 order-from-data. Weekly mini-mock: 35–40 mixed Q under time pressure; log errors and re-solve within 24 hours. Triage on exam day: Attempt your strongest patterns first (often first-order & Arrhenius), then data-heavy items. Method marks: Write the formula before numbers; carry units through every line.

Goal. In seven days, you can move from recall to exam-mode fluency by sequencing concepts → formulas → numericals → mixed mocks. Assuming 2–3 focused hours/day (adjust as needed), follow this plan and log mistakes diligently. Day-by-day plan Day 1 — Core concepts: Rate vs rate constant; average vs instantaneous; order vs molecularity; elementary vs complex. Watch a short explainer on collision theory and activation energy. Drill 25 concept MCQs. Create a half-page glossary. Day 2 — Integrated laws & half-life: Derivations and signatures (zero/first/second order). Solve 30 numericals (10 per order). Mini-mock (20 min) and review immediately. Day 3 — Arrhenius mastery: Use exponential, log, and two-point forms. Problems: find E a , predict k , temperature for rate doubling. Add unit rules (Kelvin only; align J vs kJ) to your sheet. Timed set: 12 mixed items. Day 4 — Experimental methods: Initial rates, isolation (pseudo-order), integrated plots, clock (rate &prop; 1/t*). Fit data to decide order using best linearity; practice from a noisy table. Day 5 — Mixed numericals (speed+accuracy): 35–40 problems mixing all patterns. Keep a mistake log (logs, units, Kelvin). End with a 30-minute drill. Day 6 — Full chapter mock + analysis: 60–75 min mock. Classify errors: concept vs arithmetic vs units. Patch weak areas with 10 targeted problems. Day 7 — Consolidation & rehearsal: Flash-sheet review; 25 high-yield numericals; a final 20-minute micro-mock. Quick recap: catalyst role, Arrhenius slope, order vs molecularity. Execution habits that boost marks Write knowns with units before formulas; it prevents most errors. Select the right model first (graph recognition) before computing. Use half-life shortcuts for first order (1/2, 1/4, 1/8 → 1, 2, 3 half-lives). Carry 3–4 significant figures until the final step, then round. Why Home Tuition fits Day-tagged lessons and auto-graded drills that match this schedule. Plot fitters for zero/first/second-order linearities. Timed mocks with analytics on accuracy and pace. Keep your formula sheet visible during practice; remove it for mocks to simulate exam conditions.

Goal. In seven days, you can move from recall to exam-mode fluency by sequencing concepts → formulas → numericals → mixed mocks. Assuming 2–3 focused hours/day (adjust as needed), follow this plan and log mistakes diligently. Day-by-day plan Day 1 — Core concepts: Rate vs rate constant; average vs instantaneous; order vs molecularity; elementary vs complex. Watch a short explainer on collision theory and activation energy. Drill 25 concept MCQs. Create a half-page glossary. Day 2 — Integrated laws & half-life: Derivations and signatures (zero/first/second order). Solve 30 numericals (10 per order). Mini-mock (20 min) and review immediately. Day 3 — Arrhenius mastery: Use exponential, log, and two-point forms. Problems: find E a , predict k , temperature for rate doubling. Add unit rules (Kelvin only; align J vs kJ) to your sheet. Timed set: 12 mixed items. Day 4 — Experimental methods: Initial rates, isolation (pseudo-order), integrated plots, clock (rate &prop; 1/t*). Fit data to decide order using best linearity; practice from a noisy table. Day 5 — Mixed numericals (speed+accuracy): 35–40 problems mixing all patterns. Keep a mistake log (logs, units, Kelvin). End with a 30-minute drill. Day 6 — Full chapter mock + analysis: 60–75 min mock. Classify errors: concept vs arithmetic vs units. Patch weak areas with 10 targeted problems. Day 7 — Consolidation & rehearsal: Flash-sheet review; 25 high-yield numericals; a final 20-minute micro-mock. Quick recap: catalyst role, Arrhenius slope, order vs molecularity. Execution habits that boost marks Write knowns with units before formulas; it prevents most errors. Select the right model first (graph recognition) before computing. Use half-life shortcuts for first order (1/2, 1/4, 1/8 → 1, 2, 3 half-lives). Carry 3–4 significant figures until the final step, then round. Why Home Tuition fits Day-tagged lessons and auto-graded drills that match this schedule. Plot fitters for zero/first/second-order linearities. Timed mocks with analytics on accuracy and pace. Keep your formula sheet visible during practice; remove it for mocks to simulate exam conditions.

Chemical Kinetics is a scoring chapter because it blends conceptual clarity with predictable numericals. Examiners recycle familiar formats to test whether you can convert a short prompt into the right model and compute cleanly with correct units. Use the list below as your high-yield blueprint. High-yield theory checks Definitions & contrasts: rate of reaction vs rate constant; average vs instantaneous rate; elementary vs complex reactions. Order vs molecularity: why order can be zero/fractional; why molecularity is a whole number for an elementary step; order is always experimental . Arrhenius interpretation: physical meaning of A and E a ; slope on an Arrhenius plot ( ln k vs 1/T ) equals -E a /R . Catalyst role: lowers E a , increases k , no change in equilibrium; saturation can produce zero-order behaviour. Experimental methods: method of initial rates, isolation (pseudo-order), integrated plots, and clock reactions. High-yield numericals (master these patterns) First order: ln([A]_0/[A]_t)=kt , t 1/2 =0.693/k ; compute fraction/time quickly; read slopes from ln[A] vs t . Zero order: [A]_t=[A]_0-kt , t 1/2 =[A]_0/(2k) ; completion time; beware negative concentrations beyond completion. Second order (single reactant): 1/[A]_t-1/[A]_0=kt , t 1/2 =1/(k[A]_0) . Arrhenius two-point: ln(k_2/k_1)=-(E_a/R)(1/T_2-1/T_1) for E a or k at a new T . Order from data: initial-rate tables (log-ratio exponents), integrated-plot linearity, clock method with rate &prop; 1/t* . Representative exam-style prompts First-order decomposition with given t 1/2 : find k , time to reach a percentage, or concentration at time t . Zero-order reaction with given k and [A]_0 : compute half-life and completion time. Given two k values at different temperatures: find E a ; or given E a , predict k at a new T . Initial-rates table: deduce the rate law and evaluate k with units. Clock experiment times: justify rate &prop; 1/t* and extract partial orders. Preparation tactics Build a one-page formula sheet (integrated laws, half-life relations, Arrhenius forms, unit patterns). Drill graph recognition : which plot must be linear for each order? Practice dimensional checks and unit consistency on every substitution. Home Tuition advantage Pattern-tagged question banks and mixed mocks. Step-by-step solutions with sign/unit guardrails. Analytics that highlight where accuracy or speed needs work.

Chemical Kinetics is a scoring chapter because it blends conceptual clarity with predictable numericals. Examiners recycle familiar formats to test whether you can convert a short prompt into the right model and compute cleanly with correct units. Use the list below as your high-yield blueprint. High-yield theory checks Definitions & contrasts: rate of reaction vs rate constant; average vs instantaneous rate; elementary vs complex reactions. Order vs molecularity: why order can be zero/fractional; why molecularity is a whole number for an elementary step; order is always experimental . Arrhenius interpretation: physical meaning of A and E a ; slope on an Arrhenius plot ( ln k vs 1/T ) equals -E a /R . Catalyst role: lowers E a , increases k , no change in equilibrium; saturation can produce zero-order behaviour. Experimental methods: method of initial rates, isolation (pseudo-order), integrated plots, and clock reactions. High-yield numericals (master these patterns) First order: ln([A]_0/[A]_t)=kt , t 1/2 =0.693/k ; compute fraction/time quickly; read slopes from ln[A] vs t . Zero order: [A]_t=[A]_0-kt , t 1/2 =[A]_0/(2k) ; completion time; beware negative concentrations beyond completion. Second order (single reactant): 1/[A]_t-1/[A]_0=kt , t 1/2 =1/(k[A]_0) . Arrhenius two-point: ln(k_2/k_1)=-(E_a/R)(1/T_2-1/T_1) for E a or k at a new T . Order from data: initial-rate tables (log-ratio exponents), integrated-plot linearity, clock method with rate &prop; 1/t* . Representative exam-style prompts First-order decomposition with given t 1/2 : find k , time to reach a percentage, or concentration at time t . Zero-order reaction with given k and [A]_0 : compute half-life and completion time. Given two k values at different temperatures: find E a ; or given E a , predict k at a new T . Initial-rates table: deduce the rate law and evaluate k with units. Clock experiment times: justify rate &prop; 1/t* and extract partial orders. Preparation tactics Build a one-page formula sheet (integrated laws, half-life relations, Arrhenius forms, unit patterns). Drill graph recognition : which plot must be linear for each order? Practice dimensional checks and unit consistency on every substitution. Home Tuition advantage Pattern-tagged question banks and mixed mocks. Step-by-step solutions with sign/unit guardrails. Analytics that highlight where accuracy or speed needs work.

Mechanism & what changes A catalyst introduces an alternative pathway with a lower activation energy (E a ) and sometimes altered molecular orientation factors, raising the rate constant k at the same temperature. It does not change ΔG°, the equilibrium constant K, or the final composition at equilibrium; it only helps the system reach equilibrium faster. In measured kinetics, compare k (or initial slopes) with and without catalyst to quantify acceleration. Homogeneous catalysis Same phase as reactants (e.g., I − catalysis in solution). Empirical rate law may include [Cat]: rate = k[A]^m[Cat]^p . Use initial-rate ratios to find the catalyst order p . Heterogeneous catalysis Solid catalyst, fluid reactants; steps: adsorption → surface reaction → desorption. Rate depends on surface area, active-site density, and mass transfer. Normalize rates to catalyst mass/area; report stirring speed and particle size. Experimental design & Arrhenius comparison Measure a baseline k (or initial rate) without catalyst at fixed T. Run a catalyst-loading series (vary [Cat] or catalyst mass/surface area). Measure k at multiple temperatures with/without catalyst; plot ln k vs 1/T . Worked mini-comparison: Uncatalyzed: k(298 K)=1.2×10⁻⁴ s⁻¹, k(308 K)=3.6×10⁻⁴ s⁻¹ ⇒ Ea ≈ 75 kJ·mol⁻¹Catalyzed: k(298 K)=3.0×10⁻³ s⁻¹, k(308 K)=7.5×10⁻³ s⁻¹ ⇒ Ea ≈ 48 kJ·mol⁻¹Result: Lower Ea and larger k confirm catalytic acceleration. Data treatment, controls, and quality Watch for saturation kinetics (apparent zero order at high substrate) and pre-equilibria. Diagnose mass-transfer limits: if faster stirring increases rate, you were diffusion-limited. Include blank (no catalyst) and poisoned catalyst controls. Test reusability (heterogeneous): filter–wash–reuse cycles; track turnover number (TON) and frequency (TOF).

Mechanism & what changes A catalyst introduces an alternative pathway with a lower activation energy (E a ) and sometimes altered molecular orientation factors, raising the rate constant k at the same temperature. It does not change ΔG°, the equilibrium constant K, or the final composition at equilibrium; it only helps the system reach equilibrium faster. In measured kinetics, compare k (or initial slopes) with and without catalyst to quantify acceleration. Homogeneous catalysis Same phase as reactants (e.g., I − catalysis in solution). Empirical rate law may include [Cat]: rate = k[A]^m[Cat]^p . Use initial-rate ratios to find the catalyst order p . Heterogeneous catalysis Solid catalyst, fluid reactants; steps: adsorption → surface reaction → desorption. Rate depends on surface area, active-site density, and mass transfer. Normalize rates to catalyst mass/area; report stirring speed and particle size. Experimental design & Arrhenius comparison Measure a baseline k (or initial rate) without catalyst at fixed T. Run a catalyst-loading series (vary [Cat] or catalyst mass/surface area). Measure k at multiple temperatures with/without catalyst; plot ln k vs 1/T . Worked mini-comparison: Uncatalyzed: k(298 K)=1.2×10⁻⁴ s⁻¹, k(308 K)=3.6×10⁻⁴ s⁻¹ ⇒ Ea ≈ 75 kJ·mol⁻¹Catalyzed: k(298 K)=3.0×10⁻³ s⁻¹, k(308 K)=7.5×10⁻³ s⁻¹ ⇒ Ea ≈ 48 kJ·mol⁻¹Result: Lower Ea and larger k confirm catalytic acceleration. Data treatment, controls, and quality Watch for saturation kinetics (apparent zero order at high substrate) and pre-equilibria. Diagnose mass-transfer limits: if faster stirring increases rate, you were diffusion-limited. Include blank (no catalyst) and poisoned catalyst controls. Test reusability (heterogeneous): filter–wash–reuse cycles; track turnover number (TON) and frequency (TOF).

1) Method of initial rates (log-ratio approach) Prepare several mixtures at identical temperature and total volume. Vary one reactant concentration while holding the others constant. Measure the initial rate directly (slope near t=0) or indirectly via a clock method (rate &prop; 1/t*). For a rate law rate = k[A]^m[B]^n , use two runs where only [A] changes: (rate2/rate1) = ([A]2/[A]1)^m ⇒ m = ln(rate2/rate1) / ln([A]2/[A]1) Repeat for B to obtain n . Compute k from any run.2) Integrated-rate plots (graphical order test) Zero order: [A] vs t linear, slope = −k First order: ln[A] vs t linear, slope = −k; t 1/2 = 0.693/k Second order (single reactant): 1/[A] vs t linear, slope = +k Collect a time-course data set, plot all three, and choose the one with strongest linearity (and sensible intercept). This uses more data and is resilient to noise when sampling is careful. 3) Isolation (pseudo-order) method Flood all but one reactant so their concentrations remain effectively constant. The rate law collapses to a pseudo– m th order in the limiting reactant—commonly pseudo-first order. Fit the corresponding integrated form to extract a pseudo- k' and back-calculate the true k from known, constant concentrations of the excess reactants. 4) Half-life dependence Zero order: t 1/2 = [A] 0 /(2k) (depends on [A] 0 ) First order: t 1/2 = 0.693/k (independent of [A] 0 ) Second order: t 1/2 = 1/(k[A] 0 ) (inversely depends on [A] 0 ) Worked micro-case (initial rates on A): Run 1: [A]1 = 0.10 M, rate1 = 2.5×10⁻⁵ M s⁻¹Run 2: [A]2 = 0.30 M, rate2 = 7.5×10⁻⁵ M s⁻¹rate2/rate1 = 3; [A]2/[A]1 = 3 ⇒ m = ln 3 / ln 3 = 1 Good practice Use calibrated volumetric gear; keep temperature constant (water bath). Randomize run order to avoid drift; replicate each condition. Plot residuals for your chosen model to check adequacy. Common pitfalls Calling a reaction first order just because “half-life” appears. Mixing log bases without the 2.303 factor (base-10 vs natural log). Neglecting ionic strength or pH control when mechanisms are sensitive.

1) Method of initial rates (log-ratio approach) Prepare several mixtures at identical temperature and total volume. Vary one reactant concentration while holding the others constant. Measure the initial rate directly (slope near t=0) or indirectly via a clock method (rate &prop; 1/t*). For a rate law rate = k[A]^m[B]^n , use two runs where only [A] changes: (rate2/rate1) = ([A]2/[A]1)^m ⇒ m = ln(rate2/rate1) / ln([A]2/[A]1) Repeat for B to obtain n . Compute k from any run.2) Integrated-rate plots (graphical order test) Zero order: [A] vs t linear, slope = −k First order: ln[A] vs t linear, slope = −k; t 1/2 = 0.693/k Second order (single reactant): 1/[A] vs t linear, slope = +k Collect a time-course data set, plot all three, and choose the one with strongest linearity (and sensible intercept). This uses more data and is resilient to noise when sampling is careful. 3) Isolation (pseudo-order) method Flood all but one reactant so their concentrations remain effectively constant. The rate law collapses to a pseudo– m th order in the limiting reactant—commonly pseudo-first order. Fit the corresponding integrated form to extract a pseudo- k' and back-calculate the true k from known, constant concentrations of the excess reactants. 4) Half-life dependence Zero order: t 1/2 = [A] 0 /(2k) (depends on [A] 0 ) First order: t 1/2 = 0.693/k (independent of [A] 0 ) Second order: t 1/2 = 1/(k[A] 0 ) (inversely depends on [A] 0 ) Worked micro-case (initial rates on A): Run 1: [A]1 = 0.10 M, rate1 = 2.5×10⁻⁵ M s⁻¹Run 2: [A]2 = 0.30 M, rate2 = 7.5×10⁻⁵ M s⁻¹rate2/rate1 = 3; [A]2/[A]1 = 3 ⇒ m = ln 3 / ln 3 = 1 Good practice Use calibrated volumetric gear; keep temperature constant (water bath). Randomize run order to avoid drift; replicate each condition. Plot residuals for your chosen model to check adequacy. Common pitfalls Calling a reaction first order just because “half-life” appears. Mixing log bases without the 2.303 factor (base-10 vs natural log). Neglecting ionic strength or pH control when mechanisms are sensitive.

Principle (why it’s a “clock”) In a common school-lab version, hydrogen peroxide oxidizes iodide to iodine in acidic medium. A fixed, small charge of thiosulfate “hides” the generated iodine by reducing it back to iodide. Once thiosulfate is exhausted, free iodine instantly forms a deep-blue complex with starch. Because the blue color appears only after a fixed threshold of I 2 has formed, the time to blue ( t* ) is inversely related to the initial rate of iodine production. Key reactions (H 2 O 2 /I − /H + variant) H2O2 + 2 I− + 2 H+ → I2 + 2 H2OI2 + 2 S2O3^2− → 2 I− + S4O6^2−I2 + starch → deep-blue complex (endpoint) Chemicals & setup Solution A: KI (iodide), acid (e.g., H 2 SO 4 ), starch indicator, and a fixed small amount of Na 2 S 2 O 3 . Solution B: H 2 O 2 (varied concentration to probe order). Volumetric pipettes, beakers, stopwatch, water bath (for temperature studies), white tile for endpoint clarity, PPE. Procedure (comparative runs) Keep total volume, ionic strength, and temperature constant across runs. Hold the initial thiosulfate amount fixed in every run (sets a constant I 2 threshold). Vary one reactant concentration at a time (e.g., [H 2 O 2 ]) to isolate its effect on rate. Mix A + B quickly, start the stopwatch, swirl gently, and record t* when blue appears. Repeat trials for each condition; average times to reduce random error. For temperature dependence, equilibrate both solutions at the target °C before mixing. Data analysis & calculations When the initial thiosulfate charge (threshold) is identical across runs and the total volume is constant, the initial rate is proportional to 1/ t* . Hence, if you change only one concentration between two runs, you can estimate the corresponding partial order by taking ratios. Order in H 2 O 2 (example): rate &prop; 1/t* &prop; [H2O2]^mm ≈ ln(t*1/t*2) / ln([H2O2]2/[H2O2]1) Obtain orders in iodide and acid similarly. With orders in hand, compute k from any run using the empirical rate law. For temperature dependence, build an Arrhenius plot by computing a pseudo-order k at each T and plotting ln k vs 1/T to estimate E a (slope = − E a /R). Worked mini-example Run 1: [H2O2]1 = 0.10 M, t*1 = 52 s Run 2: [H2O2]2 = 0.20 M, t*2 = 26 s t*1/t*2 = 2.00; [H2O2]2/[H2O2]1 = 2.00 ⇒ m = ln 2 / ln 2 = 1 Quality & safety Wear PPE; concentrated H 2 O 2 is an oxidizer. Use fresh starch; aged starch delays the endpoint. Assign one person to timing to avoid reaction-time variability. Rinse acid spills with plenty of water; neutralize as per lab protocol. Exam-ready tips State the mechanism, define the clock threshold, justify rate &prop; 1/t*. Show log-ratio math to extract partial orders succinctly. Include one tidy Arrhenius calculation when temperature data are given.

Principle (why it’s a “clock”) In a common school-lab version, hydrogen peroxide oxidizes iodide to iodine in acidic medium. A fixed, small charge of thiosulfate “hides” the generated iodine by reducing it back to iodide. Once thiosulfate is exhausted, free iodine instantly forms a deep-blue complex with starch. Because the blue color appears only after a fixed threshold of I 2 has formed, the time to blue ( t* ) is inversely related to the initial rate of iodine production. Key reactions (H 2 O 2 /I − /H + variant) H2O2 + 2 I− + 2 H+ → I2 + 2 H2OI2 + 2 S2O3^2− → 2 I− + S4O6^2−I2 + starch → deep-blue complex (endpoint) Chemicals & setup Solution A: KI (iodide), acid (e.g., H 2 SO 4 ), starch indicator, and a fixed small amount of Na 2 S 2 O 3 . Solution B: H 2 O 2 (varied concentration to probe order). Volumetric pipettes, beakers, stopwatch, water bath (for temperature studies), white tile for endpoint clarity, PPE. Procedure (comparative runs) Keep total volume, ionic strength, and temperature constant across runs. Hold the initial thiosulfate amount fixed in every run (sets a constant I 2 threshold). Vary one reactant concentration at a time (e.g., [H 2 O 2 ]) to isolate its effect on rate. Mix A + B quickly, start the stopwatch, swirl gently, and record t* when blue appears. Repeat trials for each condition; average times to reduce random error. For temperature dependence, equilibrate both solutions at the target °C before mixing. Data analysis & calculations When the initial thiosulfate charge (threshold) is identical across runs and the total volume is constant, the initial rate is proportional to 1/ t* . Hence, if you change only one concentration between two runs, you can estimate the corresponding partial order by taking ratios. Order in H 2 O 2 (example): rate &prop; 1/t* &prop; [H2O2]^mm ≈ ln(t*1/t*2) / ln([H2O2]2/[H2O2]1) Obtain orders in iodide and acid similarly. With orders in hand, compute k from any run using the empirical rate law. For temperature dependence, build an Arrhenius plot by computing a pseudo-order k at each T and plotting ln k vs 1/T to estimate E a (slope = − E a /R). Worked mini-example Run 1: [H2O2]1 = 0.10 M, t*1 = 52 s Run 2: [H2O2]2 = 0.20 M, t*2 = 26 s t*1/t*2 = 2.00; [H2O2]2/[H2O2]1 = 2.00 ⇒ m = ln 2 / ln 2 = 1 Quality & safety Wear PPE; concentrated H 2 O 2 is an oxidizer. Use fresh starch; aged starch delays the endpoint. Assign one person to timing to avoid reaction-time variability. Rinse acid spills with plenty of water; neutralize as per lab protocol. Exam-ready tips State the mechanism, define the clock threshold, justify rate &prop; 1/t*. Show log-ratio math to extract partial orders succinctly. Include one tidy Arrhenius calculation when temperature data are given.

Mechanism & what changes A catalyst introduces an alternative pathway with a lower activation energy (E a ) and sometimes altered molecular orientation factors, raising the rate constant k at the same temperature. It does not change ΔG°, the equilibrium constant K, or the final composition at equilibrium; it only helps the system reach equilibrium faster. In measured kinetics, compare k (or initial slopes) with and without catalyst to quantify acceleration. Homogeneous catalysis Same phase as reactants (e.g., I − catalysis in solution). Empirical rate law may include [Cat]: rate = k[A]^m[Cat]^p . Use initial-rate ratios to find the catalyst order p . Heterogeneous catalysis Solid catalyst, fluid reactants; steps: adsorption → surface reaction → desorption. Rate depends on surface area, active-site density, and mass transfer. Normalize rates to catalyst mass/area; report stirring speed and particle size. Experimental design & Arrhenius comparison Measure a baseline k (or initial rate) without catalyst at fixed T. Run a catalyst-loading series (vary [Cat] or catalyst mass/surface area). Measure k at multiple temperatures with/without catalyst; plot ln k vs 1/T . Worked mini-comparison: Uncatalyzed: k(298 K)=1.2×10⁻⁴ s⁻¹, k(308 K)=3.6×10⁻⁴ s⁻¹ ⇒ Ea ≈ 75 kJ·mol⁻¹Catalyzed: k(298 K)=3.0×10⁻³ s⁻¹, k(308 K)=7.5×10⁻³ s⁻¹ ⇒ Ea ≈ 48 kJ·mol⁻¹Result: Lower Ea and larger k confirm catalytic acceleration. Data treatment, controls, and quality Watch for saturation kinetics (apparent zero order at high substrate) and pre-equilibria. Diagnose mass-transfer limits: if faster stirring increases rate, you were diffusion-limited. Include blank (no catalyst) and poisoned catalyst controls. Test reusability (heterogeneous): filter–wash–reuse cycles; track turnover number (TON) and frequency (TOF).

Mechanism & what changes A catalyst introduces an alternative pathway with a lower activation energy (E a ) and sometimes altered molecular orientation factors, raising the rate constant k at the same temperature. It does not change ΔG°, the equilibrium constant K, or the final composition at equilibrium; it only helps the system reach equilibrium faster. In measured kinetics, compare k (or initial slopes) with and without catalyst to quantify acceleration. Homogeneous catalysis Same phase as reactants (e.g., I − catalysis in solution). Empirical rate law may include [Cat]: rate = k[A]^m[Cat]^p . Use initial-rate ratios to find the catalyst order p . Heterogeneous catalysis Solid catalyst, fluid reactants; steps: adsorption → surface reaction → desorption. Rate depends on surface area, active-site density, and mass transfer. Normalize rates to catalyst mass/area; report stirring speed and particle size. Experimental design & Arrhenius comparison Measure a baseline k (or initial rate) without catalyst at fixed T. Run a catalyst-loading series (vary [Cat] or catalyst mass/surface area). Measure k at multiple temperatures with/without catalyst; plot ln k vs 1/T . Worked mini-comparison: Uncatalyzed: k(298 K)=1.2×10⁻⁴ s⁻¹, k(308 K)=3.6×10⁻⁴ s⁻¹ ⇒ Ea ≈ 75 kJ·mol⁻¹Catalyzed: k(298 K)=3.0×10⁻³ s⁻¹, k(308 K)=7.5×10⁻³ s⁻¹ ⇒ Ea ≈ 48 kJ·mol⁻¹Result: Lower Ea and larger k confirm catalytic acceleration. Data treatment, controls, and quality Watch for saturation kinetics (apparent zero order at high substrate) and pre-equilibria. Diagnose mass-transfer limits: if faster stirring increases rate, you were diffusion-limited. Include blank (no catalyst) and poisoned catalyst controls. Test reusability (heterogeneous): filter–wash–reuse cycles; track turnover number (TON) and frequency (TOF).

1) Method of initial rates (log-ratio approach) Prepare several mixtures at identical temperature and total volume. Vary one reactant concentration while holding the others constant. Measure the initial rate directly (slope near t=0) or indirectly via a clock method (rate &prop; 1/t*). For a rate law rate = k[A]^m[B]^n , use two runs where only [A] changes:(rate2/rate1) = ([A]2/[A]1)^m ⇒ m = ln(rate2/rate1) / ln([A]2/[A]1)Repeat for B to obtain n . Compute k from any run. 2) Integrated-rate plots (graphical order test) Zero order: [A] vs t linear, slope = −k First order: ln[A] vs t linear, slope = −k; t 1/2 = 0.693/k Second order (single reactant): 1/[A] vs t linear, slope = +k Collect a time-course data set, plot all three, and choose the one with strongest linearity (and sensible intercept). This uses more data and is resilient to noise when sampling is careful. 3) Isolation (pseudo-order) method Flood all but one reactant so their concentrations remain effectively constant. The rate law collapses to a pseudo– m th order in the limiting reactant—commonly pseudo-first order. Fit the corresponding integrated form to extract a pseudo- k' and back-calculate the true k from known, constant concentrations of the excess reactants. 4) Half-life dependence Zero order: t 1/2 = [A] 0 /(2k) (depends on [A] 0 ) First order: t 1/2 = 0.693/k (independent of [A] 0 ) Second order: t 1/2 = 1/(k[A] 0 ) (inversely depends on [A] 0 ) Worked micro-case (initial rates on A): Run 1: [A]1 = 0.10 M, rate1 = 2.5×10⁻⁵ M s⁻¹Run 2: [A]2 = 0.30 M, rate2 = 7.5×10⁻⁵ M s⁻¹rate2/rate1 = 3; [A]2/[A]1 = 3 ⇒ m = ln 3 / ln 3 = 1 Good practice Use calibrated volumetric gear; keep temperature constant (water bath). Randomize run order to avoid drift; replicate each condition. Plot residuals for your chosen model to check adequacy. Common pitfalls Calling a reaction first order just because “half-life” appears. Mixing log bases without the 2.303 factor (base-10 vs natural log). Neglecting ionic strength or pH control when mechanisms are sensitive.

1) Method of initial rates (log-ratio approach) Prepare several mixtures at identical temperature and total volume. Vary one reactant concentration while holding the others constant. Measure the initial rate directly (slope near t=0) or indirectly via a clock method (rate &prop; 1/t*). For a rate law rate = k[A]^m[B]^n , use two runs where only [A] changes:(rate2/rate1) = ([A]2/[A]1)^m ⇒ m = ln(rate2/rate1) / ln([A]2/[A]1)Repeat for B to obtain n . Compute k from any run. 2) Integrated-rate plots (graphical order test) Zero order: [A] vs t linear, slope = −k First order: ln[A] vs t linear, slope = −k; t 1/2 = 0.693/k Second order (single reactant): 1/[A] vs t linear, slope = +k Collect a time-course data set, plot all three, and choose the one with strongest linearity (and sensible intercept). This uses more data and is resilient to noise when sampling is careful. 3) Isolation (pseudo-order) method Flood all but one reactant so their concentrations remain effectively constant. The rate law collapses to a pseudo– m th order in the limiting reactant—commonly pseudo-first order. Fit the corresponding integrated form to extract a pseudo- k' and back-calculate the true k from known, constant concentrations of the excess reactants. 4) Half-life dependence Zero order: t 1/2 = [A] 0 /(2k) (depends on [A] 0 ) First order: t 1/2 = 0.693/k (independent of [A] 0 ) Second order: t 1/2 = 1/(k[A] 0 ) (inversely depends on [A] 0 ) Worked micro-case (initial rates on A): Run 1: [A]1 = 0.10 M, rate1 = 2.5×10⁻⁵ M s⁻¹Run 2: [A]2 = 0.30 M, rate2 = 7.5×10⁻⁵ M s⁻¹rate2/rate1 = 3; [A]2/[A]1 = 3 ⇒ m = ln 3 / ln 3 = 1 Good practice Use calibrated volumetric gear; keep temperature constant (water bath). Randomize run order to avoid drift; replicate each condition. Plot residuals for your chosen model to check adequacy. Common pitfalls Calling a reaction first order just because “half-life” appears. Mixing log bases without the 2.303 factor (base-10 vs natural log). Neglecting ionic strength or pH control when mechanisms are sensitive.

In chemical kinetics, the rate of reaction describes how quickly reactants are converted into products during a chemical process. This measurement is fundamental for students preparing for competitive exams like NEET, JEE, and board examinations. Understanding reaction rates allows chemists and engineers to optimize conditions for desired yields, control product quality, and predict how a reaction will proceed under specific conditions. The rate of a reaction is defined as the change in concentration of reactants or products per unit time. Mathematically:Rate= -Δ[Reactant]/Δt or Δ[Product]/ΔtHere, the negative sign in the reactant term shows that reactant concentration decreases over time.Rates can be instantaneous (at a specific moment) or average (over a time interval). Instantaneous rates are often calculated using the slope of a concentration-time curve. Factors influencing rate measurement: Concentration of reactants: Higher concentrations typically lead to faster reactions because more particles collide per second. Temperature: Higher temperatures increase kinetic energy, leading to more frequent and energetic collisions. Catalysts: Speed up reactions without being consumed. Surface area: Finer particles expose more surface area, accelerating reaction rates. Units: For zero-order reactions: mol L⁻¹ s⁻¹ For first-order reactions: s⁻¹ For second-order reactions: L mol⁻¹ s⁻¹ Actionable Insights / Study Tips Memorize definitions of average and instantaneous rate for quick recall in exams. Practice unit conversions—these often appear in numerical questions. Link the graphical interpretation (concentration vs. time, rate vs. concentration) with equations. In Infinity Learn’s online modules, use interactive simulations to visualize real-time rate changes. Summary Table Term Meaning Reaction Rate Change in concentration per unit time Average Rate Over a time interval Instantaneous Rate At a specific instant

In chemical kinetics, the rate of reaction describes how quickly reactants are converted into products during a chemical process. This measurement is fundamental for students preparing for competitive exams like NEET, JEE, and board examinations. Understanding reaction rates allows chemists and engineers to optimize conditions for desired yields, control product quality, and predict how a reaction will proceed under specific conditions. The rate of a reaction is defined as the change in concentration of reactants or products per unit time. Mathematically:Rate= -Δ[Reactant]/Δt or Δ[Product]/ΔtHere, the negative sign in the reactant term shows that reactant concentration decreases over time.Rates can be instantaneous (at a specific moment) or average (over a time interval). Instantaneous rates are often calculated using the slope of a concentration-time curve. Factors influencing rate measurement: Concentration of reactants: Higher concentrations typically lead to faster reactions because more particles collide per second. Temperature: Higher temperatures increase kinetic energy, leading to more frequent and energetic collisions. Catalysts: Speed up reactions without being consumed. Surface area: Finer particles expose more surface area, accelerating reaction rates. Units: For zero-order reactions: mol L⁻¹ s⁻¹ For first-order reactions: s⁻¹ For second-order reactions: L mol⁻¹ s⁻¹ Actionable Insights / Study Tips Memorize definitions of average and instantaneous rate for quick recall in exams. Practice unit conversions—these often appear in numerical questions. Link the graphical interpretation (concentration vs. time, rate vs. concentration) with equations. In Infinity Learn’s online modules, use interactive simulations to visualize real-time rate changes. Summary Table Term Meaning Reaction Rate Change in concentration per unit time Average Rate Over a time interval Instantaneous Rate At a specific instant

Core idea. Activation energy, E a , quantifies the barrier that reactants must overcome. Temperature shifts the fraction of molecules above this barrier. Numerically, you will mostly use the two-point Arrhenius equation. Arrhenius (exponential): k = A e −E a /(RT) Two-point form: ln(k₂/k₁) = −(E a /R)(1/T₂ − 1/T₁) Use Kelvin only ; keep E a in J·mol⁻¹ if R = 8.314 J·mol⁻¹·K⁻¹ Worked example 1 — Find E a from two k–T pairs k1 = 1.5×10⁻³ s⁻¹ at 298 K; k2 = 6.0×10⁻³ s⁻¹ at 308 Kln(k2/k1) = ln 4 = 1.3863Ea = −R × ln(k2/k1) / (1/308 − 1/298) ≈ 1.06×10⁵ J·mol⁻¹ = 105.8 kJ·mol⁻¹ Worked example 2 — Predict k at a higher temperature Given Ea = 85.0 kJ·mol⁻¹, k1 = 2.2×10⁻³ s⁻¹ at 303 Kk2 = k1 exp[ −Ea/R (1/323 − 1/303) ] ≈ 1.78×10⁻² s⁻¹ Worked example 3 — Temperature to double the rate constant T1 = 300 K, Ea = 50.0 kJ·mol⁻¹, k2 = 2k1ln 2 = −Ea/R (1/T2 − 1/T1) ⇒ 1/T2 = 1/T1 − (R/Ea) ln 2T2 ≈ 310.7 K (≈ +10.7 K to double k near 300 K) Common mistakes Using °C in Arrhenius calculations (always convert to Kelvin). Mismatching energy units (kJ vs J); align E a with R. Dropping the negative sign or swapping T₁ and T₂ in (1/T₂ − 1/T₁). Over-rounding intermediate steps; keep 3–4 significant figures. Exam routine Write the two-point equation first; then substitute with units. For Arrhenius plots (ln k vs 1/T), identify slope = −E a /R quickly. Present E a neatly in kJ·mol⁻¹ with the correct sign and magnitude.

Core idea. Activation energy, E a , quantifies the barrier that reactants must overcome. Temperature shifts the fraction of molecules above this barrier. Numerically, you will mostly use the two-point Arrhenius equation. Arrhenius (exponential): k = A e −E a /(RT) Two-point form: ln(k₂/k₁) = −(E a /R)(1/T₂ − 1/T₁) Use Kelvin only ; keep E a in J·mol⁻¹ if R = 8.314 J·mol⁻¹·K⁻¹ Worked example 1 — Find E a from two k–T pairs k1 = 1.5×10⁻³ s⁻¹ at 298 K; k2 = 6.0×10⁻³ s⁻¹ at 308 Kln(k2/k1) = ln 4 = 1.3863Ea = −R × ln(k2/k1) / (1/308 − 1/298) ≈ 1.06×10⁵ J·mol⁻¹ = 105.8 kJ·mol⁻¹ Worked example 2 — Predict k at a higher temperature Given Ea = 85.0 kJ·mol⁻¹, k1 = 2.2×10⁻³ s⁻¹ at 303 Kk2 = k1 exp[ −Ea/R (1/323 − 1/303) ] ≈ 1.78×10⁻² s⁻¹ Worked example 3 — Temperature to double the rate constant T1 = 300 K, Ea = 50.0 kJ·mol⁻¹, k2 = 2k1ln 2 = −Ea/R (1/T2 − 1/T1) ⇒ 1/T2 = 1/T1 − (R/Ea) ln 2T2 ≈ 310.7 K (≈ +10.7 K to double k near 300 K) Common mistakes Using °C in Arrhenius calculations (always convert to Kelvin). Mismatching energy units (kJ vs J); align E a with R. Dropping the negative sign or swapping T₁ and T₂ in (1/T₂ − 1/T₁). Over-rounding intermediate steps; keep 3–4 significant figures. Exam routine Write the two-point equation first; then substitute with units. For Arrhenius plots (ln k vs 1/T), identify slope = −E a /R quickly. Present E a neatly in kJ·mol⁻¹ with the correct sign and magnitude.

Why half-life matters. Half-life connects concept and calculation. Know how t 1/2 behaves for each order and you can move between fraction remaining and time in seconds. First order: t 1/2 = 0.693/k (independent of [A] 0 ) Zero order: t 1/2 = [A] 0 /(2k) Second order (single reactant): t 1/2 = 1/(k[A] 0 ) Sample 1 — First order Given: k = 0.032 min⁻¹. (a) Find t 1/2 . (b) Time to reach 12.5% of the initial concentration. (a) t1/2 = 0.693/0.032 = 21.7 min(b) 12.5% = 1/8 ⇒ three half-lives ⇒ ≈ 65.1 minExact: t = ln(1/0.125)/0.032 = (ln 8)/0.032 = 65.0 min Sample 2 — Zero order Given: k = 2.5×10⁻³ M s⁻¹, [A]₀ = 0.40 M. (a) Half-life? (b) Completion time? (a) t1/2 = [A]0/(2k) = 0.40/(2×2.5×10⁻³) = 80 s(b) Completion t = [A]0/k = 0.40/(2.5×10⁻³) = 160 s Sample 3 — Second order Given: [A]₀ = 0.10 M, k = 0.25 M⁻¹ min⁻¹. (a) Half-life? (b) [A] after 20 min? (a) t1/2 = 1/(k[A]0) = 1/(0.25×0.10) = 40 min(b) 1/[A]t − 1/[A]0 = kt ⇒ [A]t = [A]0/(1 + k[A]0 t) [A]20 = 0.10/(1 + 0.25×0.10×20) = 0.0667 M Order recognition via graphs Zero: [A] vs t is linear (slope −k) First: ln[A] vs t is linear (slope −k) Second: 1/[A] vs t is linear (slope +k) Units & pitfall checks Zero-order k: M·time⁻¹; First-order k: time⁻¹; Second-order k: M⁻¹·time⁻¹ Do not assume first order just because “half-life” appears—check dependence on [A]₀. For zero order, do not extrapolate beyond [A]t = 0; negative concentrations are nonphysical.

Why half-life matters. Half-life connects concept and calculation. Know how t 1/2 behaves for each order and you can move between fraction remaining and time in seconds. First order: t 1/2 = 0.693/k (independent of [A] 0 ) Zero order: t 1/2 = [A] 0 /(2k) Second order (single reactant): t 1/2 = 1/(k[A] 0 ) Sample 1 — First order Given: k = 0.032 min⁻¹. (a) Find t 1/2 . (b) Time to reach 12.5% of the initial concentration. (a) t1/2 = 0.693/0.032 = 21.7 min(b) 12.5% = 1/8 ⇒ three half-lives ⇒ ≈ 65.1 minExact: t = ln(1/0.125)/0.032 = (ln 8)/0.032 = 65.0 min Sample 2 — Zero order Given: k = 2.5×10⁻³ M s⁻¹, [A]₀ = 0.40 M. (a) Half-life? (b) Completion time? (a) t1/2 = [A]0/(2k) = 0.40/(2×2.5×10⁻³) = 80 s(b) Completion t = [A]0/k = 0.40/(2.5×10⁻³) = 160 s Sample 3 — Second order Given: [A]₀ = 0.10 M, k = 0.25 M⁻¹ min⁻¹. (a) Half-life? (b) [A] after 20 min? (a) t1/2 = 1/(k[A]0) = 1/(0.25×0.10) = 40 min(b) 1/[A]t − 1/[A]0 = kt ⇒ [A]t = [A]0/(1 + k[A]0 t) [A]20 = 0.10/(1 + 0.25×0.10×20) = 0.0667 M Order recognition via graphs Zero: [A] vs t is linear (slope −k) First: ln[A] vs t is linear (slope −k) Second: 1/[A] vs t is linear (slope +k) Units & pitfall checks Zero-order k: M·time⁻¹; First-order k: time⁻¹; Second-order k: M⁻¹·time⁻¹ Do not assume first order just because “half-life” appears—check dependence on [A]₀. For zero order, do not extrapolate beyond [A]t = 0; negative concentrations are nonphysical.

First-order kinetics appear frequently in exams because they’re algebra-friendly and yield clean exponential laws. The fastest path to accurate answers is: recognize the pattern, choose the right integrated form, keep units consistent, and show crisp steps. Core recognition & key formulas Definition: Rate = −d[A]/dt = k[A] Integrated (with initial concentration): ln([A] 0 /[A] t ) = k t Two-point form: ln([A] t1 /[A] t2 ) = k (t 2 − t 1 ) Half-life: t 1/2 = 0.693/k (constant, order’s fingerprint) Units: k has units of time −1 (s −1 , min −1 ) Worked example 1 (classic single interval) [A]0 = 0.100 M, [A]t = 0.025 M at t = 6.00 mink = (1/6.00) ln(0.100/0.025) = (1/6.00) ln 4 = 0.231 min⁻¹Half-life: t1/2 = 0.693/0.231 ≈ 3.00 minPredict [A] at 15.0 min: [A]15 = 0.100 e^(−0.231×15) ≈ 3.13×10⁻³ M Worked example 2 (two-point data, no [A] 0 ) [A]40s = 0.80 M, [A]100s = 0.50 Mk = (1/60) ln(0.80/0.50) = 7.83×10⁻³ s⁻¹t1/2 = 0.693/k ≈ 88.5 sTime to reach 0.10 M from 0.80 M:t = (1/k) ln(0.80/0.10) = ln 8 / 7.83×10⁻³ ≈ 265.5 s ≈ 4.43 min Common mistakes Mixing °C with K when temperature appears in related steps. Switching log bases without the 2.303 factor. Reading slope from the wrong plot (for first order use ln[A] vs t). Unit mismatch: if time is in minutes, keep k in min⁻¹. Exam shortcuts Constant half-life → first order → jump to t 1/2 = 0.693/k. Two data points? Use the two-point form; no need for [A]0. Use the “every half-life halves concentration” rule for quick estimates.

First-order kinetics appear frequently in exams because they’re algebra-friendly and yield clean exponential laws. The fastest path to accurate answers is: recognize the pattern, choose the right integrated form, keep units consistent, and show crisp steps. Core recognition & key formulas Definition: Rate = −d[A]/dt = k[A] Integrated (with initial concentration): ln([A] 0 /[A] t ) = k t Two-point form: ln([A] t1 /[A] t2 ) = k (t 2 − t 1 ) Half-life: t 1/2 = 0.693/k (constant, order’s fingerprint) Units: k has units of time −1 (s −1 , min −1 ) Worked example 1 (classic single interval) [A]0 = 0.100 M, [A]t = 0.025 M at t = 6.00 mink = (1/6.00) ln(0.100/0.025) = (1/6.00) ln 4 = 0.231 min⁻¹Half-life: t1/2 = 0.693/0.231 ≈ 3.00 minPredict [A] at 15.0 min: [A]15 = 0.100 e^(−0.231×15) ≈ 3.13×10⁻³ M Worked example 2 (two-point data, no [A] 0 ) [A]40s = 0.80 M, [A]100s = 0.50 Mk = (1/60) ln(0.80/0.50) = 7.83×10⁻³ s⁻¹t1/2 = 0.693/k ≈ 88.5 sTime to reach 0.10 M from 0.80 M:t = (1/k) ln(0.80/0.10) = ln 8 / 7.83×10⁻³ ≈ 265.5 s ≈ 4.43 min Common mistakes Mixing °C with K when temperature appears in related steps. Switching log bases without the 2.303 factor. Reading slope from the wrong plot (for first order use ln[A] vs t). Unit mismatch: if time is in minutes, keep k in min⁻¹. Exam shortcuts Constant half-life → first order → jump to t 1/2 = 0.693/k. Two data points? Use the two-point form; no need for [A]0. Use the “every half-life halves concentration” rule for quick estimates.

With Rate = −d[A]/dt = k , integrate directly to get [A]_t = [A]_0 − k t . The concentration-time plot is linear; half-life is t 1/2 = [A]_0/(2k) , which depends on initial concentration. When zero order arises Zero-order kinetics typically appear when a system is capacity-limited: catalyst surfaces saturated with substrate, light-driven reactions at constant photon flux, or steady-state production where the bottleneck is processing capacity, not reactant availability. Under these conditions, changing [A] doesn’t change the rate until saturation ends. Derivation and implications Write: −d[A]/dt = k (rate independent of [A] ). Integrate: ∫ d[A] = −k ∫ dt with limits [A]_0 → [A]_t and 0 → t . Obtain: [A]_t − [A]_0 = −k t → [A]_t = [A]_0 − k t . Completion time: set [A]_t = 0 → t = [A]_0/k . Half-life: set [A]_t = [A]_0/2 → t 1/2 = [A]_0/(2k) . Worked example [A]0 = 0.50 M, k = 2.0×10^−3 M·s^−1After 100 s: [A]t = 0.50 − (2.0×10^−3)(100) = 0.30 MHalf-life: t1/2 = 0.50/(2×2.0×10^−3) = 125 sCompletion: t = 0.50/(2.0×10^−3) = 250 s Checks, boundaries, and units Linear [A] vs t with constant slope −k indicates zero order within the tested range. Units of k : concentration·time −1 (e.g., M·s −1 ). Don’t extrapolate beyond [A]_t = 0 ; negative concentrations are non-physical.

With Rate = −d[A]/dt = k , integrate directly to get [A]_t = [A]_0 − k t . The concentration-time plot is linear; half-life is t 1/2 = [A]_0/(2k) , which depends on initial concentration. When zero order arises Zero-order kinetics typically appear when a system is capacity-limited: catalyst surfaces saturated with substrate, light-driven reactions at constant photon flux, or steady-state production where the bottleneck is processing capacity, not reactant availability. Under these conditions, changing [A] doesn’t change the rate until saturation ends. Derivation and implications Write: −d[A]/dt = k (rate independent of [A] ). Integrate: ∫ d[A] = −k ∫ dt with limits [A]_0 → [A]_t and 0 → t . Obtain: [A]_t − [A]_0 = −k t → [A]_t = [A]_0 − k t . Completion time: set [A]_t = 0 → t = [A]_0/k . Half-life: set [A]_t = [A]_0/2 → t 1/2 = [A]_0/(2k) . Worked example [A]0 = 0.50 M, k = 2.0×10^−3 M·s^−1After 100 s: [A]t = 0.50 − (2.0×10^−3)(100) = 0.30 MHalf-life: t1/2 = 0.50/(2×2.0×10^−3) = 125 sCompletion: t = 0.50/(2.0×10^−3) = 250 s Checks, boundaries, and units Linear [A] vs t with constant slope −k indicates zero order within the tested range. Units of k : concentration·time −1 (e.g., M·s −1 ). Don’t extrapolate beyond [A]_t = 0 ; negative concentrations are non-physical.

For Rate = −d[A]/dt = k[A], separate variables and integrate to obtain ln([A]_0/[A]_t) = k t (or log [A]_t = log [A]_0 − (k/2.303) t ). The half-life is t 1/2 =0.693/k , independent of initial concentration. Step-by-step derivation Write the differential rate law: −d[A]/dt = k[A] . Separate: d[A]/[A] = −k dt . Integrate with limits: ∫_[A0]^[At] d[A]/[A] = −k ∫_0^t dt . Obtain: ln [A]_t − ln [A]_0 = −k t → ln([A]_0/[A]_t) = k t . Base-10 form: log [A]_t = log [A]_0 − (k/2.303) t . Graph signatures & half-life ln [A] vs t is linear (slope −k ); log [A] vs t has slope −k/2.303 . Half-life: set [A]_t = [A]_0/2 → t 1/2 =0.693/k (constant across any [A]_0 ). Worked example [A]0 = 0.100 M, k = 2.0×10^−3 s^−1, t = 500 sln([A]0/[A]t) = (2.0×10^−3)(500) = 1.0 ⇒ [A]t = 0.100/e ≈ 0.0368 Mt1/2 = 0.693/2.0×10^−3 ≈ 346.5 s Quality checks & exam habits Always integrate with limits to avoid missing the constant of integration. Keep logs consistent (stick to natural log or base-10 within a solution). Verify units: for first order, k has units of time −1 .

For Rate = −d[A]/dt = k[A], separate variables and integrate to obtain ln([A]_0/[A]_t) = k t (or log [A]_t = log [A]_0 − (k/2.303) t ). The half-life is t 1/2 =0.693/k , independent of initial concentration. Step-by-step derivation Write the differential rate law: −d[A]/dt = k[A] . Separate: d[A]/[A] = −k dt . Integrate with limits: ∫_[A0]^[At] d[A]/[A] = −k ∫_0^t dt . Obtain: ln [A]_t − ln [A]_0 = −k t → ln([A]_0/[A]_t) = k t . Base-10 form: log [A]_t = log [A]_0 − (k/2.303) t . Graph signatures & half-life ln [A] vs t is linear (slope −k ); log [A] vs t has slope −k/2.303 . Half-life: set [A]_t = [A]_0/2 → t 1/2 =0.693/k (constant across any [A]_0 ). Worked example [A]0 = 0.100 M, k = 2.0×10^−3 s^−1, t = 500 sln([A]0/[A]t) = (2.0×10^−3)(500) = 1.0 ⇒ [A]t = 0.100/e ≈ 0.0368 Mt1/2 = 0.693/2.0×10^−3 ≈ 346.5 s Quality checks & exam habits Always integrate with limits to avoid missing the constant of integration. Keep logs consistent (stick to natural log or base-10 within a solution). Verify units: for first order, k has units of time −1 .

The Arrhenius equation connects the rate constant k to temperature T : k = A e^{-E_a/RT} , where E a is the activation energy and A is the frequency factor. Taking logs gives a linear form, ln k = ln A − E_a/(R T) , enabling you to determine E a from an Arrhenius plot.Chemical reactions require collisions with sufficient energy and proper orientation. The Maxwell–Boltzmann distribution predicts the fraction of molecules above an energy threshold. Combining that fraction (proportional to e^{-E_a/RT} ) with a collision-orientation term ( A ) yields the Arrhenius expression. As T rises, a larger fraction has energy ≥ E a , so k increases. Derivation outline: Start with the energy distribution: the fraction with E ≥ E a &prop; e^{-E_a/RT} . Account for collision frequency and orientation via A . Combine to get k = A e^{-E_a/RT} ; take logs for ln k = ln A − E_a/(R T) . Use the linear plot of ln k vs 1/T to extract E a (slope = − E a / R ). Worked example Given k 1 =1.2×10 −3 s −1 at 298 K and k 2 =4.8×10 −3 s −1 at 308 K: ln(k2/k1) = −Ea/R · (1/T2 − 1/T1)ln 4 = 1.386 = −Ea/8.314 · (1/308 − 1/298)Ea ≈ 5.2×10^4 J·mol^−1 = 52 kJ·mol^−1 Common mistakes to avoid Using °C instead of Kelvin in the equation. Dropping the negative sign in the linear slope. Assuming A is constant over very wide temperature spans without verification. In solutions, always write the exponential form, the log form, label slope/intercept, and end with a one-line physical interpretation (energy barrier & temperature sensitivity).

The Arrhenius equation connects the rate constant k to temperature T : k = A e^{-E_a/RT} , where E a is the activation energy and A is the frequency factor. Taking logs gives a linear form, ln k = ln A − E_a/(R T) , enabling you to determine E a from an Arrhenius plot.Chemical reactions require collisions with sufficient energy and proper orientation. The Maxwell–Boltzmann distribution predicts the fraction of molecules above an energy threshold. Combining that fraction (proportional to e^{-E_a/RT} ) with a collision-orientation term ( A ) yields the Arrhenius expression. As T rises, a larger fraction has energy ≥ E a , so k increases. Derivation outline: Start with the energy distribution: the fraction with E ≥ E a &prop; e^{-E_a/RT} . Account for collision frequency and orientation via A . Combine to get k = A e^{-E_a/RT} ; take logs for ln k = ln A − E_a/(R T) . Use the linear plot of ln k vs 1/T to extract E a (slope = − E a / R ). Worked example Given k 1 =1.2×10 −3 s −1 at 298 K and k 2 =4.8×10 −3 s −1 at 308 K: ln(k2/k1) = −Ea/R · (1/T2 − 1/T1)ln 4 = 1.386 = −Ea/8.314 · (1/308 − 1/298)Ea ≈ 5.2×10^4 J·mol^−1 = 52 kJ·mol^−1 Common mistakes to avoid Using °C instead of Kelvin in the equation. Dropping the negative sign in the linear slope. Assuming A is constant over very wide temperature spans without verification. In solutions, always write the exponential form, the log form, label slope/intercept, and end with a one-line physical interpretation (energy barrier & temperature sensitivity).

For JEE and NEET aspirants, understanding factors affecting reaction rate is crucial for both theory and numerical sections. This knowledge not only explains why reactions behave differently under varied conditions but also forms the basis for industrial process optimization. Detailed Factors: Concentration of Reactants – More particles in a given volume increase collision frequency. Temperature – Raises kinetic energy; per Arrhenius equation, rate constant k increases exponentially with temperature. Catalysts – Provide alternative pathways with lower activation energy. Surface Area – In heterogeneous reactions, greater exposed area leads to faster rates. Pressure (for gases) – Higher pressure effectively increases gas concentration. Nature of Reactants – Ionic reactions are usually faster than covalent ones. Arrhenius Equation Role k = Ae −Ea /RT This relationship quantitatively shows how temperature and activation energy control rate constants. Study Tips When answering in exams, structure your points: list factor, explain, give example. Use Infinity Learn’s interactive temperature-rate graphs to visualize the effect. Practice MCQs where a single change (e.g., doubling concentration) affects rate.

For JEE and NEET aspirants, understanding factors affecting reaction rate is crucial for both theory and numerical sections. This knowledge not only explains why reactions behave differently under varied conditions but also forms the basis for industrial process optimization. Detailed Factors: Concentration of Reactants – More particles in a given volume increase collision frequency. Temperature – Raises kinetic energy; per Arrhenius equation, rate constant k increases exponentially with temperature. Catalysts – Provide alternative pathways with lower activation energy. Surface Area – In heterogeneous reactions, greater exposed area leads to faster rates. Pressure (for gases) – Higher pressure effectively increases gas concentration. Nature of Reactants – Ionic reactions are usually faster than covalent ones. Arrhenius Equation Role k = Ae −Ea /RT This relationship quantitatively shows how temperature and activation energy control rate constants. Study Tips When answering in exams, structure your points: list factor, explain, give example. Use Infinity Learn’s interactive temperature-rate graphs to visualize the effect. Practice MCQs where a single change (e.g., doubling concentration) affects rate.

Both order and molecularity describe aspects of chemical reactions, but they are distinct concepts. For competitive exams, confusing them can cost marks. Order is derived experimentally, while molecularity is based on the reaction mechanism. Order of a Reaction Definition: The sum of the powers of concentration terms in the rate law equation. Example: For rate law Rate=k[A] m [B] n , the order = m + n Features: Can be zero, fractional, or whole numbers. Determined experimentally, not from the balanced equation. Indicates how the rate depends on concentration. Molecularity of a Reaction Definition: The number of reacting species (atoms, ions, molecules) colliding in a single elementary step. Features: Always a whole number (1, 2, or 3). Determined from the reaction mechanism. Cannot be zero. Differences Between Order and Molecularity Feature Order Molecularity Basis Experimental rate law Reaction mechanism Value Zero, fractional, or integer Always a whole number Applicability Overall reaction Single step only

Both order and molecularity describe aspects of chemical reactions, but they are distinct concepts. For competitive exams, confusing them can cost marks. Order is derived experimentally, while molecularity is based on the reaction mechanism. Order of a Reaction Definition: The sum of the powers of concentration terms in the rate law equation. Example: For rate law Rate=k[A] m [B] n , the order = m + n Features: Can be zero, fractional, or whole numbers. Determined experimentally, not from the balanced equation. Indicates how the rate depends on concentration. Molecularity of a Reaction Definition: The number of reacting species (atoms, ions, molecules) colliding in a single elementary step. Features: Always a whole number (1, 2, or 3). Determined from the reaction mechanism. Cannot be zero. Differences Between Order and Molecularity Feature Order Molecularity Basis Experimental rate law Reaction mechanism Value Zero, fractional, or integer Always a whole number Applicability Overall reaction Single step only

Chemical Kinetics Class 12 Notes – Rate of Reaction, Order, and Integrated Rate Laws

Stuck on Chemical Kinetics Numericals? Go from 0 to Full Marks.

CBSE Chemical Kinetics notes can be personified as an "Overwhelmed Achiever." This student, typically in Class 12, is not struggling with the subject due to a lack of effort but from a specific, critical gap between theoretical knowledge and practical application. They can follow derivations of complex formulas like the Arrhenius equation, k=Ae−Ea/RT, in a classroom setting but feel paralyzed when faced with unseen numerical problems in an exam. This disconnect creates significant anxiety and a fear of underperforming in the high-stakes CBSE board exams, which they see as a crucial gateway to prestigious universities. Their primary pain point is not a lack of resources but the overwhelming nature of them, leading to frustration and a loss of confidence despite long hours of study.

Stop wasting time on confusing books. Get the only CBSE-focused notes with step-by-step methods to solve any question and ace your board exams. 100% aligned with the latest syllabus.

Trusted by 15,000+ CBSE Students from India's Top Schools

FORGET MEMORIZING: Our notes explain the 'why' behind every formula so you actually understand it.
MASTER NUMERICALS: Get proven, step-by-step guides for every single type of problem.
REVISE IN MINUTES: Use our one-page mind maps and formula sheets to revise the entire chapter before any test.
SCORE WITH CERTAINTY: Practice with a handpicked bank of the most important Past Year Questions (PYQs).

Introduction

Chemical kinetics is the branch of chemistry which deals with the rates of chemical reactions, factors affecting the rate of reaction and the mechanism of the reaction.

For any reaction, aA + bB → cC + dD the rate is given by
Rate = - (1/a) Δ[A]/Δt = - (1/b) Δ[B]/Δt = (1/c) Δ[C]/Δt = (1/d) Δ[D]/Δt

Here, minus sign indicates the decrease in concentration of reactants.
Rate of disappearance or appearance of any substance does not involve stoichiometric coefficients.

Hence, rate of disappearance of A is
- Δ[A]/Δt

e.g.
N₂ + 3H₂ → 2NH₃
Rate = -Δ[N₂]/Δt = -Δ[H₂]/3Δt = Δ[NH₃]/2Δt

Average rate

Average rate = (Change in concentration)/(Time interval) = (x₂ - x₁)/(t₂ - t₁) = Δx/Δt. The time interval is large here.

Instantaneous rate

Instantaneous rate is the rate of a reaction at a particular instant of time and is equal to the slope of tangent drawn at that point of time in the plot of concentration vs time.

Units of rate of a reaction are mol L^–1 time^–1 or atm time^–1 (for gaseous reaction).

THE RATE OF A REACTION DEPENDS ON THE FOLLOWING FACTORS

(i) Concentration of the reactant: Greater the concentration of the reactants, faster is the rate.

(ii) Temperature: Generally, the rate of reaction doubles for every 10K rise in temperature.

(iii) Catalyst: It generally increases the rate by decreasing the activation energy of reaction.

(iv) Sun light: Photochemical reactions require the presence of light.

(v) Surface area of the reactants: Greater the surface area, faster is the reaction. That is why powdered coal burns faster than dump of coal.

LAW OF MASS ACTION

It states that the rate of a reaction is directly proportional to the product of active masses of the reactants each raised to the power equals to its stoichiometric coefficients.

RATE LAW

It states that the rate of a reaction is directly proportional to the product of active masses of the reactants raised to the power by the number of moles of reactants used in slowest step.
For a reaction, aA + bB → cC + dD
Rate law is given as Rate = k [A]^α [B]^β, where α, β are the number of moles of reactants involved in slowest step.

CHARACTERISTICS OF k

k is constant for a particular reaction, it depends upon temperature but not on the concentration of reactants.

Units of rate constant for n^th order reaction is given by

1 / [conc]ⁿ⁻¹ × 1 / time
Hence, for first order reaction the units of k is time⁻¹.

ORDER OF A REACTION

It is the sum of powers of different combining compounds in the rate law expression. For the above reaction order = α + β.
Order is an experimental concept and it may be zero, fraction or integer.
Rate constant (k) is the rate of reaction when the concentration of each reactant is unity.

MOLECULARITY

Molecularity of a reaction is the number of atoms or ions or molecules colliding simultaneously so as to result into a chemical reaction. It is always a whole number. Molecularity of a complex reaction has no significance as such. It is the molecularity of the slowest step (rate determining step) which has significance. Hence the overall molecularity can be taken as the molecularity of the slowest step.Note: Reactions having order or molecularity more than 3 are rare. Dissociation of chlorate (4 KClO₃ → 3 KClO₄ + KCl) is an example of 4^th order reaction. Order of a reaction changes with conditions like temperature, pressure etc. but molecularity does not.

Example: The rate of reaction between A and B increases by a factor of 100, when the concentration of A is changed from 0.1 mol L⁻¹ to 1 mol L⁻¹. The order of reaction with respect to A is

(A) 10

(B) 1

(D) 2

Solution: (D).

Change of 10 times in conc. results in changing the rate by 10² times. Hence order = 2.

MECHANISM

Mechanism of a reaction is the series of steps of overall reaction. For the reaction, 2NO₂ + F₂ → 2NO₂F; Rate = k[NO₂][F₂] Hence, the proposed mechanism is NO₂ + F₂ slow → NO₂F + F NO₂ + F fast → NO₂F Hence, the rate law depends on the slowest step of the mechanism only.

DIFFERENT TYPES OF REACTIONS

(i) Parallel or concurrent reactions: In such reactions reactant is converted parallely into different products.

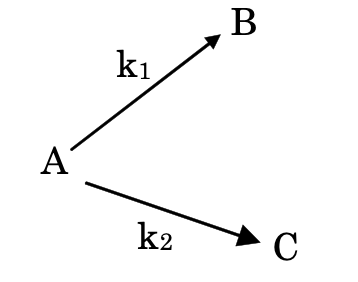
chemical kinetics machanism

-d[A]dt = k₁[A] + k₂[A]

d[B]dt = k₁[A]

d[C]dt = k₂[A]

Hence, ratio of the two products, [B][C] = k₁k₂

Percentage of B = k₁k₁ + k₂ × 100

Percentage of C = k₂k₁ + k₂ × 100

(ii) Sequential reactions:

A —_k₁→ B —_k₂→ C

d[A]/dt = -k₁[A]

d[B]/dt = k₁[A] − k₂[B]

d[C]/dt = k₂[B]

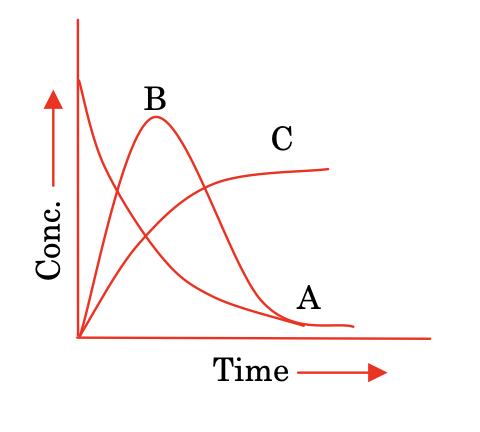
sequential reaction

As the steady state of B is reached, the concentration of B becomes constant. Hence, rate of formation and rate of consumption of B are equal.

(iii) Reactions involving intermediate in equilibrium with reactants.

A + B k₁ ⇌ k₂ X →_k₃ C

‘X’ is intermediate
Rate = k₃ [X] (i)

K_eq. = k₁/k₂ = [X]/([A][B])
Hence, [X] = (k₁/k₂) [A][B]

Putting in equation (i),
∴ Rate of reaction = (k₁ k₃ / k₂) [A][B]

Reactions at equilibrium

e.g. I₂ + H₂ k₁ ⇌ k₂ 2HI

Rate of reaction = ½ d[HI]/dt = k₁[H₂][I₂] − k₂[HI]²

INTEGRATED RATE EXPRESSIONS
(i) Zero order reaction
For a zero order reaction, A → Product
Rate = – d[A]/dt = k[A]⁰ = k
On integrating, we get [A] = –kt + [A]₀

or, k = (1/t) [[A]₀ – [A]]

where [A]₀ – initial concentration of reactant
[A] – concentration present at time ‘t’

Half life: It is the time when reaction is 50% complete.

Hence, at t_1/2, [A] = [A]₀ / 2

t = (1/k) [ [A]₀ – ([A]₀ / 2) ] = [A]₀ / 2k

When whole of the substance has reacted, i.e., [A] = 0

t = [A]₀ / k

Graphical representations of zero order reaction

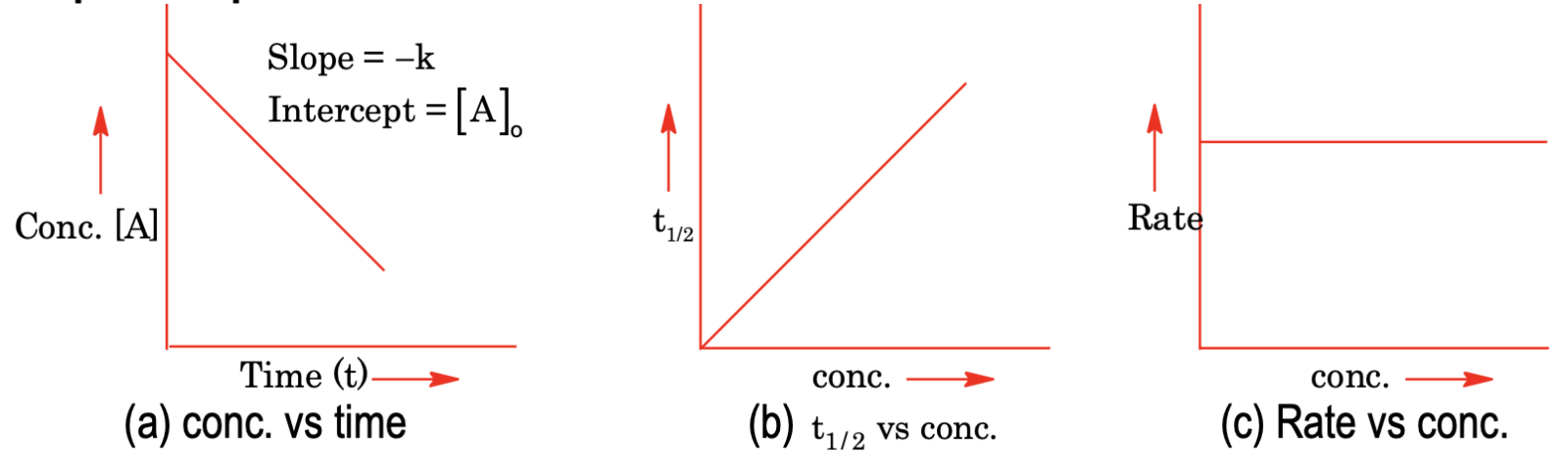
Examples of zero order reaction

H₂ + Cl₂ ——_hv——> 2HCl
2NH₃ ——_{Mo or hv}——> N₂ + 3H₂

(ii) First order reactions

For a first order reaction, A → Product

Rate = -dA/dt = k[A]

On integrating, we get
k = (2.303 / t) log([A]₀ / [A]) or k = (2.303 / t) log(a / (a - x))

where [A]₀ or a is the initial concentration of reactant. [A] is the present concentration and x is the amount reacted.

Exponential form for first order reaction is [A] = [A]₀ e^−kt.

Half life: Half life for a first order reaction is independent of the initial concentration and is given by
t_1/2 = 0.693 / k

Graphical representations of first order reaction

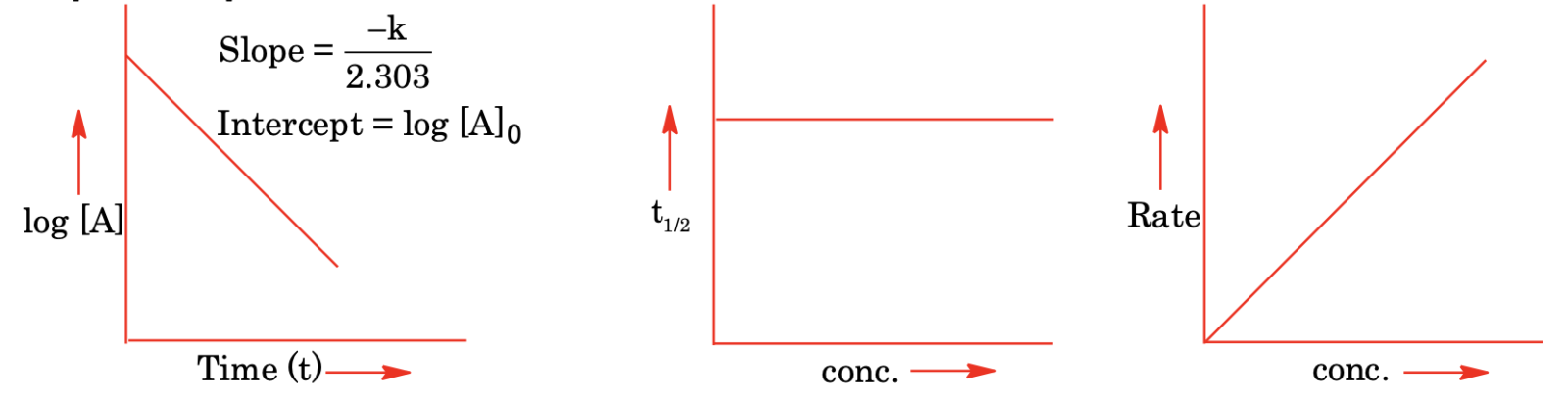
The amount of reactant left after ‘n’ half lives is given by
[A] = [A]₀ / 2ⁿ
where n = Number of half lives =
Total time (t) / Half life (t_1/2)

Modified expressions for rate constants of some common reactions of 1^st order

(a) N₂O₅ → 2NO₂ + ½O₂
k = (2.303 / t) × log(V_∞ / (V_∞ - V_t))
(V_t = Volume of O₂ after time t and V_∞ = Volume of O₂ after infinite time)

(b) NH₄NO₂(aq.) → 2H₂O + N₂
Same as above (V_t and V_∞ are the volumes of N₂ after time t and infinite time respectively)

(c) H₂O₂ → H₂O + ½O₂
k = (2.303 / t) × log(V₀ / V_t)
(V₀ and V_t are the volumes of KMnO₄ solution used for titration of same volume of reaction mixture at zero time (initially) and after time t).

(d) CH₃COOC₂H₅ + H₂O →^H⁺ CH₃COOH + C₂H₅OH

k = ^2.303⁄_t log [ (V_∞ − V₀) ⁄ (V_∞ − V_t) ]
(V₀, V_t, and V_∞ are the volumes of standard NaOH solution used for titration of same volume of the reaction mixture after times 0, t and ∞ respectively).

(e) Inversion of cane sugar:
C₁₂H₂₂O₁₁ + H₂O → C₆H₁₂O₆ + C₆H₁₂O₆
sucrose(d−) Glucose(d+) Fructose(ℓ−)

k = ^2.303⁄_t log [ (r₀ − r_∞) ⁄ (r_t − r_∞) ]
(r₀, r_t and r_∞ are the polarimetric reading after times 0, t and ∞ respectively).

(iii) Second order reactions
For a second order reaction, A → Product
d[A]/dt = −k[A]² or dx/dt = k(a − x)²
k = (1/t) [ x / a(a − x) ] or 1/(a − x) = kt + 1/a
t_1/2 = 1/ka or 1 / k [A₀]

Half life: Half life for n^th order reaction is given by
t_1/2 = [2ⁿ⁻¹ − 1] ⁄ [(n − 1) k [A]₀^{n − 1}]
or t_1/2 ∝ 1 / [A]₀ⁿ⁻¹, (n ≠ 1)

Graphical representations of second order reactions

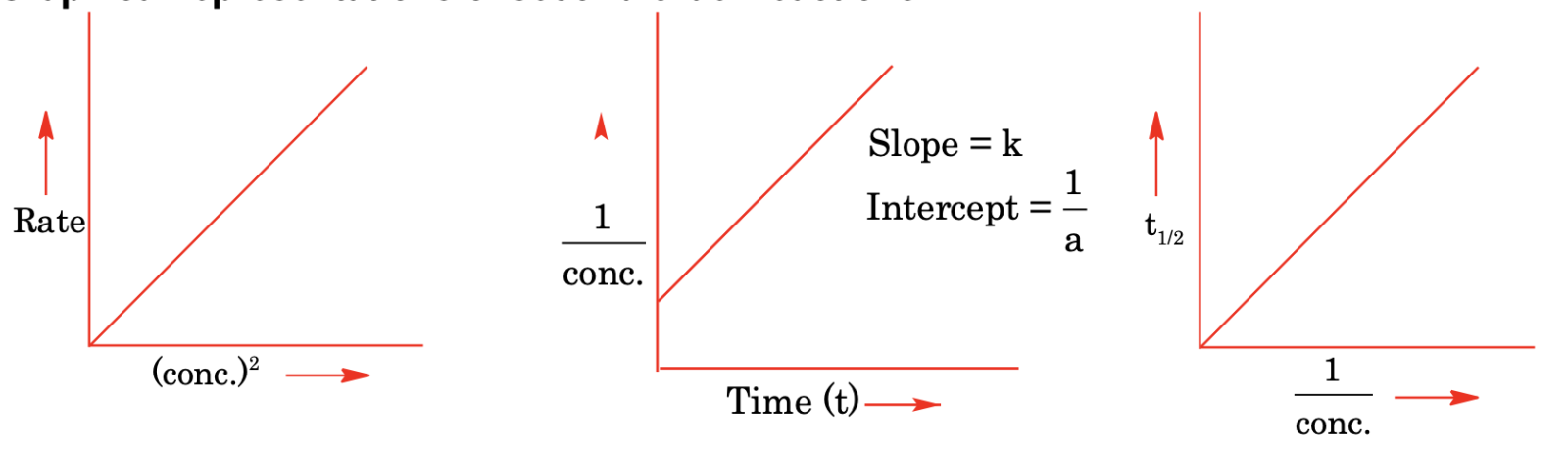
Examples of second order reaction

(a) 2NO₂ + F₂ ⟶ 2NO₂F
(b) 2HI ⟶ H₂ + I₂
(c) CH₃COOC₂H₅NaOH ⟶ CH₃COONa + C₂H₅OH

Examples of third order reaction

(a) 2NO + O₂ ⟶ 2NO₂
(b) 2NO + 2Br₂ ⟶ 2NOBr

Fractional order

CH₃CHO ⟶ CH₄ + CO; Rate = k[CH₃CHO]^3/2
H₂ + Br₂ ⟶ 2HBr; Rate = k[H₂][Br₂]^1/2

Pseudo unimolecular reactions

These reactions are not truly of first order but become first order under some specific conditions, e.g. hydrolysis of ester in acid medium, hydrolysis of cane sugar etc.

Example: Time required to decompose half of the substance for nth order reaction is inversely proportional to

(A) aⁿ⁺¹

(B) a^n-1

(D) a^1-n

Solution: (B).

t_1/2 ∝ 1 / a^n-1

COLLISION THEORY

Rate of reaction does not depend upon the total number of collisions but on the number of effective collisions (fraction of molecules having energy greater than threshold or activation energy).

Rate = −dx/dt = Z × f

where Z = Collision frequency
f = e^−Ea/RT is the number of effective collisions

Temperature coefficient

Temperature coefficient (μ) = k₃₀₈ / k₂₉₈, μ lies between 2 and 3.

Generally rate of reactions doubles for every 10°C rise in temperature. If the temperature of the reaction having temperature coefficient μ is increased from T₁ to T₂, rate is increased by μⁿ times where n = (T₂ − T₁)/10.

Threshold energy

It is the minimum amount of energy required for a reaction to take place.

Activation energy (E_a)

It is the energy given to the reactant to reach the threshold value of energy.

activation energy chemial kinetics

Arrhenius Equation Notes

Note: Catalyst lowers the activation energy by changing the reaction path and hence increases the rate of reaction.

Arrhenius equation

It gives the effect of temperature on rate constant.

k = A e^-Ea/RT

where

E_a – Activation energy (J/mol)
A – Frequency factor (Arrhenius constant)
T – Temperature in Kelvin
R – Gas constant

Taking log, we get

log k = log A – E_a / 2.303 RT

or,

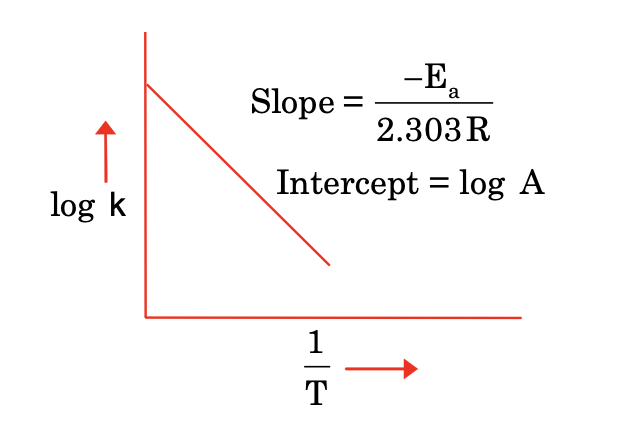
log (k₂/k₁) = E_a / 2.303 R (1/T₁ – 1/T₂) where T₂ > T₁

[Graph: Log k vs 1/T]

Slope = –E_a / 2.303 R
Intercept = log A

chemical kinetics

PHOTOCHEMICAL REACTIONS

Photochemical reactions takes place in the presence of light, ΔH for such reactions can not be negative.
Temperature has no effect on the rate of such reaction but intensity of light affects the rate.

Photosensitizer

Photosensitizer is the substance which on addition helps to start a photochemical reaction.

Quantum yield of efficiency, Q =

Number of molecules reacting in given time / Total number of quanta absorbed in that time

Example: A chemical reaction was carried out at 300 K and 280 K. The rate constants were found to be k₁ and k₂ respectively. Then

(A) k₂ = 4 k₁

(B) k₂ = 2 k₁

(D) k₂ = 0.5 k₁

Solution: (C).

For every 10°C rise in temperature doubles the rate constant hence 20°C in temperature decrease will decrease the rate 4 times.

RADIOACTIVITY

It is the phenomena of emission of certain kinds of radiations by some unstable elements.

α – rays

α – rays have charge +2 and mass 4 units, deflected by magnetic and electric field, their penetrating power is low, ionizing power is high, produce fluorescence in ZnS screen.

β – rays

β – rays are same as electrons, their penetrating power is higher than α – rays.

γ – rays

γ – rays have no charge and mass, their velocity is same as electromagnetic radiations, not deflected by electric and magnetic field, their penetrating power is more than β – rays and ionization power is very low.

Note: Nuclear forces are 10²¹ times stronger than electrostatic forces.

GROUP DISPLACEMENT LAW (GIVEN BY SODDY, FAJAN AND RUSSELL)

(i) Emission of an α–particle results in decrease of two units in atomic number and four units in mass number (new element is two positions on the left in the periodic table).
²³⁸₉₂U → ²³⁴₉₀Th + ⁴₂He (α–particle)
α–decay produces isodiapheres. New element so formed is two positions on the left in the periodic table.

(ii) β–decay results one unit increase in atomic number of daughter element but no change in mass. It produces isobars. New element so formed is one position on the right in the periodic table.
¹⁴₆C → ¹⁴₇N + ⁰₋₁e (β–particle)

(iii) γ–rays are emitted after α and β–rays. No change in the position of the element so formed in the periodic table.

Electron does not exist in nucleus, but is emitted by the nucleus by conversion of neutron to proton.
n → p + ⁰₋₁e

Radioactive disintegrations follow first order kinetics.
Activity of radioactive element
Activity of radioactive element is its rate of disintegration.
dN/dt = −λ × N

Units of activity are curie (Ci), becquerel (Bq), rutherford (Rd) and disintegrations per second.
1 curie (Ci) = 3.7 × 10¹⁰ dps, 1 Bq = 1 dps
1 Rd = 10⁶ dps

Decay constant

For radioactive element decay constant is given by

λ = (2.303 / t) log ( a / (a − x) ) or λ = (2.303 / t) log ( N₀ / N )

where N₀ is the initial amount and N is the amount left after time t.

t_1/2 = 0.693 / λ and t_average = 1 / λ

Rate of disintegration does not depends on temperature.

Packing fraction

Packing fraction = (Isotopic mass − Mass number) / Mass number × 10⁴

It can be −ve, +ve or zero.

Mass defect

Δm = (Σ m_product − Σ m_reactants) amu

Binding energy

Binding energy = Δm × 931.5 MeV, (1 MeV = 1.6 × 10⁻¹³ J)

Binding energy per nucleon

Binding energy per nucleon = Binding energy / Mass number

More the binding energy per nucleon, more is the stability.

Any nucleus will be stable when the neutron–proton ratio (n/p) is close to unity.

Important disintegration series

Series	Name of series	Starting element	Stable product
4n	Thorium series	Th – 232	Pb – 208
4n + 1	Neptunium series	Np – 237	Bi – 209
4n + 2	Uranium series	U – 238	Pb – 206
4n + 3	Actinium series	U – 235	Pb – 207

When divided by 4 these give remainder of 0, 1, 2 and 3 respectively.

Artificial transmutation

Artificial transmutation is the process of converting one element to another element.

e.g. ¹⁴₇N + ⁴₂He → ¹⁷₈O + ¹₁H

The above reaction can be represented as ¹⁴₇N (α, p) ¹⁷₈O.

Best bombarding particles are neutrons because they have no charge.

Artificial or induced radioactivity

Artificial or induced radioactivity is the process of converting stable nuclei to radioactive isotope.

e.g. ⁴₂He + ²⁷₁₃Al → ³⁰₁₅P + ¹₀n

(stable) (radioactive)

Cyclotron is used to accelerate bombarding particles (protons, neutrons etc.).

Nuclear fission

It is the process of splitting of a heavier nuclei into smaller atoms by bombarding subatomic particles.

²³⁵₉₂U + ¹₀n → ¹⁴⁰₅₆Ba + ⁹³₃₆Kr + 3 · ¹₀n

Neutrons emitted by this reaction bombard more uranium atoms and the reaction goes on. It is called chain reaction.

Note:²³⁸₉₂U (more abundant isotope) is non radioactive.

Transuranic elements

Transuranic elements come after Uranium and are called synthetic elements.

Nuclear reactor

Nuclear reactor is a device to produce energy by fission reaction of ²³⁵₉₅U.

Control rods (made up of boron or cadmium) are used to absorb neutrons and moderators (heavy water or graphite) are used to slow down the speed of neutron.

Breeder reactor

In it the non fissionable material (U²³⁸) is first converted into fissionable Pu²³⁵ to continue chain reaction.

Atom bomb

Atom bomb is based on the principle of fission reaction.

Nuclear fusion

It is the process in which light elements combine to form bigger atoms. This takes place at very high temperature, i.e. in the sun. Hence, these are called thermonuclear reactions.

4 ¹₁H → ⁴₂He + 2 ⁰₊₁e + γ + Energy

Hydrogen bomb

Hydrogen bomb is based on the principle of fusion reaction. Hydrogen bomb involves fission in the centre to start the nuclear fusion reaction.

Note: For the same mass of element energy released in fusion reaction is greater than the energy released in fission reaction.

Applications of radioactivity

In medicines.
In carbon dating (to find age of fossils)
¹⁴₆C → ¹⁴₇N + ⁰_-1e
In geological dating (to find age of minerals).

Tracers

Tracers are the isotopes used in very small quantities to detect the path of reaction.

Neutron activation analysis

In this trace of one element in another is found by activating it with neutrons bombardment.

Magic numbers

The nuclei whose nuclear shells contain 2, 8, 20, 50, 80 or 126 neutrons or protons are more stable. These numbers are called magic numbers.

Spallation reactions

Spallation reactions are similar to fission reactions. They differ in the fact that they are brought about by high energy bombarding particles.

Frequently Asked Questions

Principle (why it’s a “clock”)

In a common school-lab version, hydrogen peroxide oxidizes iodide to iodine in acidic medium. A fixed, small charge of thiosulfate “hides” the generated iodine by reducing it back to iodide. Once thiosulfate is exhausted, free iodine instantly forms a deep-blue complex with starch. Because the blue color appears only after a fixed threshold of I₂ has formed, the time to blue (t*) is inversely related to the initial rate of iodine production.

Key reactions (H₂O₂/I⁻/H⁺ variant)

H2O2 + 2 I− + 2 H+ → I2 + 2 H2O
I2 + 2 S2O3^2− → 2 I− + S4O6^2−
I2 + starch → deep-blue complex (endpoint)

Chemicals & setup

Solution A: KI (iodide), acid (e.g., H₂SO₄), starch indicator, and a fixed small amount of Na₂S₂O₃.
Solution B: H₂O₂ (varied concentration to probe order).
Volumetric pipettes, beakers, stopwatch, water bath (for temperature studies), white tile for endpoint clarity, PPE.

Procedure (comparative runs)

Keep total volume, ionic strength, and temperature constant across runs.
Hold the initial thiosulfate amount fixed in every run (sets a constant I₂ threshold).
Vary one reactant concentration at a time (e.g., [H₂O₂]) to isolate its effect on rate.
Mix A + B quickly, start the stopwatch, swirl gently, and record t* when blue appears.
Repeat trials for each condition; average times to reduce random error.
For temperature dependence, equilibrate both solutions at the target °C before mixing.

Data analysis & calculations

When the initial thiosulfate charge (threshold) is identical across runs and the total volume is constant, the initial rate is proportional to 1/t*. Hence, if you change only one concentration between two runs, you can estimate the corresponding partial order by taking ratios.

Order in H₂O₂ (example):

rate ∝ 1/t* ∝ [H2O2]^m
m ≈ ln(t*1/t*2) / ln([H2O2]2/[H2O2]1)

Obtain orders in iodide and acid similarly. With orders in hand, compute k from any run using the empirical rate law. For temperature dependence, build an Arrhenius plot by computing a pseudo-order k at each T and plotting ln k vs 1/T to estimate E_a (slope = −E_a/R).

Worked mini-example

Run 1: [H2O2]1 = 0.10 M, t*1 = 52 s
Run 2: [H2O2]2 = 0.20 M, t*2 = 26 s
t*1/t*2 = 2.00; [H2O2]2/[H2O2]1 = 2.00 ⇒ m = ln 2 / ln 2 = 1

Quality & safety

Wear PPE; concentrated H₂O₂ is an oxidizer.
Use fresh starch; aged starch delays the endpoint.
Assign one person to timing to avoid reaction-time variability.
Rinse acid spills with plenty of water; neutralize as per lab protocol.

Exam-ready tips

State the mechanism, define the clock threshold, justify rate ∝ 1/t*.
Show log-ratio math to extract partial orders succinctly.
Include one tidy Arrhenius calculation when temperature data are given.

S.no	Formulas List
1.	Liquid Solutions
2.	Electrochemistry
3.	Chemical Kinetics
4.	Ores and Metallurge
5.	P-Block Elements
6.	D-Block and Co-ordination Compounds
7.	Chemistry of Heavy Metals
8.	Alkyl and Aryl Halides
9.	Alcohol phenol and ether
10.	Aldehyde and Ketone

Term	Meaning
Reaction Rate	Change in concentration per unit time
Average Rate	Over a time interval
Instantaneous Rate	At a specific instant

Feature	Order	Molecularity
Basis	Experimental rate law	Reaction mechanism
Value	Zero, fractional, or integer	Always a whole number
Applicability	Overall reaction	Single step only

Chemical Kinetics

Stuck on Chemical Kinetics Numericals? Go from 0 to Full Marks.

Introduction

Frequently Asked Questions

Related Links

Become one of thousands of satisfied students!

Frequently Asked Questions