Electrochemistry

INTRODUCTION

This unit is studied under the following three heads:

(a) Redox reaction or oxidation–reduction reactions.

(b) Electrolysis and electrochemical cells.

(c) Electrical conductances.

REDOX REACTIONS

Those reactions in which the process of reduction and oxidation takes place simultaneously are called redox reaction. For example,

MnO₄⁻ + C₂O₄²⁻ → Mn²⁺ + CO₂

In the above reaction

(i) MnO₄⁻ is reduced and hence it is called oxidizing agent.

(ii) C₂O₄²⁻ is oxidized and hence it is called reducing agent.

Electronic concept

Loss of electrons is oxidation while gain of electrons is known as reduction.

MnO₄⁻ + 8H⁺ + 5e⁻ → Mn²⁺ (reduction)

C₂O₄²⁻ → 2CO₂ + 2e⁻ (oxidation)

Oxidation number (O.N.) Criteria

Increase in O.N. of an element means oxidation while a decrease means reduction.
Oxidation Number (O.N.) of an element in a compound or ion is defined as the charge developed on that element when all the bond pairs are shifted on more electronegative elements, e.g. O.N. of H & Cl in H^δ+ – Cl^δ− are +1 and –1 respectively.

Oxidation number (O.N.) Criteria

Increase in O.N. of an element means oxidation while a decrease means reduction. Oxidation Number (O.N.) of an element in a compound or ion is defined as the charge developed on that element when all the bond pairs are shifted on more electronegative elements, e.g. O.N. of H & Cl in H^δ⁺ − Cl^δ⁻ are +1 and −1 respectively.

Rules for calculating O.N.

(i) In free states, O.N. of elements is zero, for example, O.N. of H, Cl, N etc are zero.

(ii) In combined state O.N. of

(a) F is always −1.

(b) O is −2, in peroxides (O⁻¹ − O⁻¹) it is −1 and in super oxide (O₂⁻) it is −1/2.

(c) H: +1, except in metallic hydrides such as NaH, in which its oxidation number is −1.

(d) Alkali metals is always +1.

(e) Alkaline earth metals is always +2.

(iii) Algebric sum of the oxidation numbers of all the elements is equal to zero or equal to its change in case of complex ion.

KMnO₄: oxidation number of K = +1

Oxidation number of O = −2

Let oxidation number of Mn be x.

then 1 + x + 4(−2) = 0

x = +7

Note: Oxidation number of an element can never exceed its valence electrons.

Oxidation state (O.S.)

It the oxidation number per atom e.g. in K₂Cr₂O₇ oxidation number of Cr is 12 while OS is + 6

n–factor in redox reactions: It is the number of moles of electrons lost or gained per mole of reducing or oxidizing agent, e.g.

MnO₄⁻ + 8H⁺ + 5e⁻ → Mn²⁺ + 4H₂O

Here n–factor of this half reaction is +5
= 7 − 2 = 5.

Cr₂O₇²⁻ → 2Cr³⁺

n = 12 − 6 = 6

Balancing of redox reactions

Rule I: First find the n–factor of the two half reactions separately. For example,

• Ox. half reaction
  n = 8 − 6 = 2
  MnO₄⁻ + C₂O₄²⁻ → Mn²⁺ + 2CO₂
• Red. half reaction
  n = 7 − 2 = 5

Rule II: Now cross multiply the n–factors, i.e. multiply the n–factor of reduction half reaction in oxidation half reaction & vice–versa.

2MnO₄^- + 5C₂O₄^2- → 5Mn²⁺ + 10CO₂

Rule III: Balancing of H and O atom

Case I: In Acidic medium: (O–atoms are balanced first than H).

Add desired no. of H₂O molecules on the side deficient in O–atoms and add adequate no. of H⁺ ions on the side deficient in H–atom, i.e.

2MnO₄^- + 5C₂O₄^2- + 16H⁺ → 5Mn²⁺ + 10CO₂ + 8H₂O (balanced equation)

Case II: In Basic medium: Add desired no. of H₂O molecules on the side rich in O– atoms and double number of OH⁻ ions on the opposite side for balancing of O–atom. Add desired no of H₂O molecule on the side deficient in H–atom and same number of OH⁻ ions on the opposites side to balance H–atoms.

Disproportionation reactions
The redox reactions in which same substance is oxidized as well as reduced simultaneously are called disproportionation reactions e.g.

 Reduction
2Cu+ → Cu2+ + Cu0
 Oxidation

ELECTROLYSIS AND ELECTROCHEMICAL CELLS

The process in which ions are discharged at oppositely charged electrodes by the passage of electricity into the molten or aqueous solution of electrolyte is called electrolysis, e.g. when electricity is passed through molten solution of NaCl, Na(s) is deposited at cathode (reduction) and Cl₂ gas is evolved at anode (oxidation). The process of electrolysis is carried out in a cell known as electrolytic cell.

At cathode (Reduction takes place):

Na⁺ + e⁻ → Na(s)

At anode (Oxidation takes place):

2Cl⁻ → Cl₂(g) + 2e⁻

(1) In an electrolytic cell, the chemical reaction is not spontaneous, i.e. ΔG > 0, and so, it is carried out at the expense of electricity.

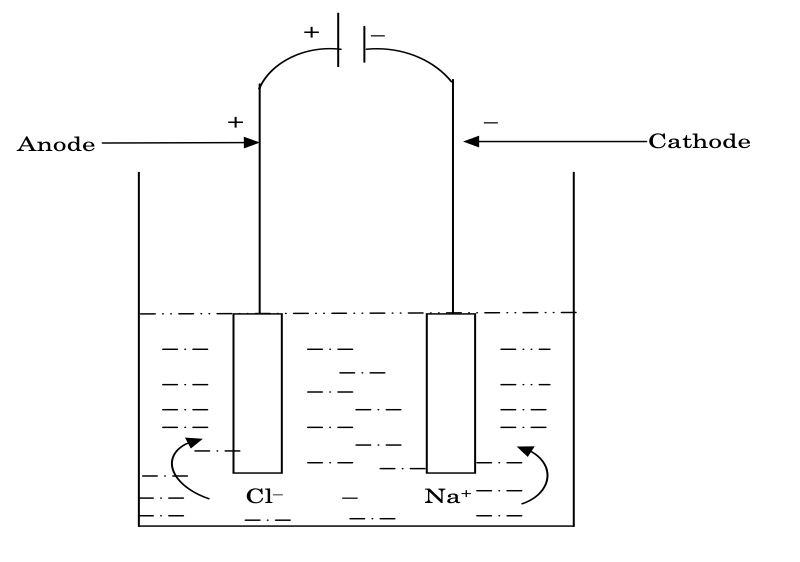
(1) In an electrolytic cell, the chemical reaction is not spontaneous, i.e. and so, it is carried out at the expense of electricity.

LAWS OF ELECTROLYSIS

Faraday’s first law of electrolysis

It states that the amount of a substance deposited at an electrode is directly proportional to the amount of electricity passed through it, i.e. w ∝ q
or,
w = Z × q = Z × i × t
(Z = electrochemical equivalent of metal)
and, Z = E\F
(w = Eit/F))

where, E = equivalent weight of metal, F = faraday constant = charge on 1 mole of electrons.
It is the charge which can deposit 1 g equivalent weight of a metal at the electrodes
1 F = N_s × e = 96500 coulomb

Faraday’s Second law of electrolysis

It states that, w₁/w₂ = E₁/E_2, i.e. the weight of metals deposited at the respective electrodes are in the ratio of their equivalent weights if same amount of electricity is passed through their aqueous solutions.

Example. 0.02 Faraday of electricity is passed through an aqueous solution of 0.001 mole aq. CuSO₄ solution. Moles of Cu deposited at cathode are.

(A) 0.01 mole

(B) 0.001 mole

(C) 0.02 mole

(D) 0.04 mole

Solution: (B). Cu²⁺ + 2e⁻ → Cu

Since 2F electricity can deposit 1 mole Cu.

∴ 0.001 mole will be deposited by 0.002 F electricity

Hence, whole of Cu²⁺ion will be deposited & remaining electricity (0.02 − 0.002) F will electrolyse water now.

ELECTRO CHEMICAL CELLS OR GALVANIC CELLS OR VOLTAIC CELLS

It is a device which produces electrical energy as a result of a redox reaction. Like electrolytic cells, in Galvanic cells also, reduction takes place at cathode and oxidation at anode. But in Galvanic cells, anode is negative and cathode is positive (reverse polarity to electrolytic cells) and the chemical reaction taking place in the cell is spontaneous is ΔG < 0.

Working of a Galvanic cell

Let us consider a Zn–Cu cell in which zinc is undergoing oxidation at anode and copper is undergoing reduction at cathode, i.e. cell reaction is

Zn(s) + Cu²⁺(aq) → Zn²⁺(aq) + Cu(s)

In Galvanic cells reduction and oxidation half reaction takes place in two different containers which are connected through a voltmeter which reads the cell potential (E_cell). The schematic diagram of a galvanic cell is given in the diagram. In the Galvanic cells, anode compartment (e.g. Zn/ZnSO₄) is kept on the L.H.S while cathode compartment (CuSO₄/Cu) is kept on the R.H.S. In each compartment a metal rod is dipped into the solution of its own ions, e.g. Zn rod is dipped into Zn²⁺ ions and Cu rod is dipped into Cu²⁺ ions solution. As soon as the two electrodes are connected, the cell reaction starts and a momentary current flows.

At anode: (oxidation)

Zn(s) → Zn²⁺(aq) + 2e^-

At cathode (reduction)

Cu²⁺ + 2e^- → Cu(s)

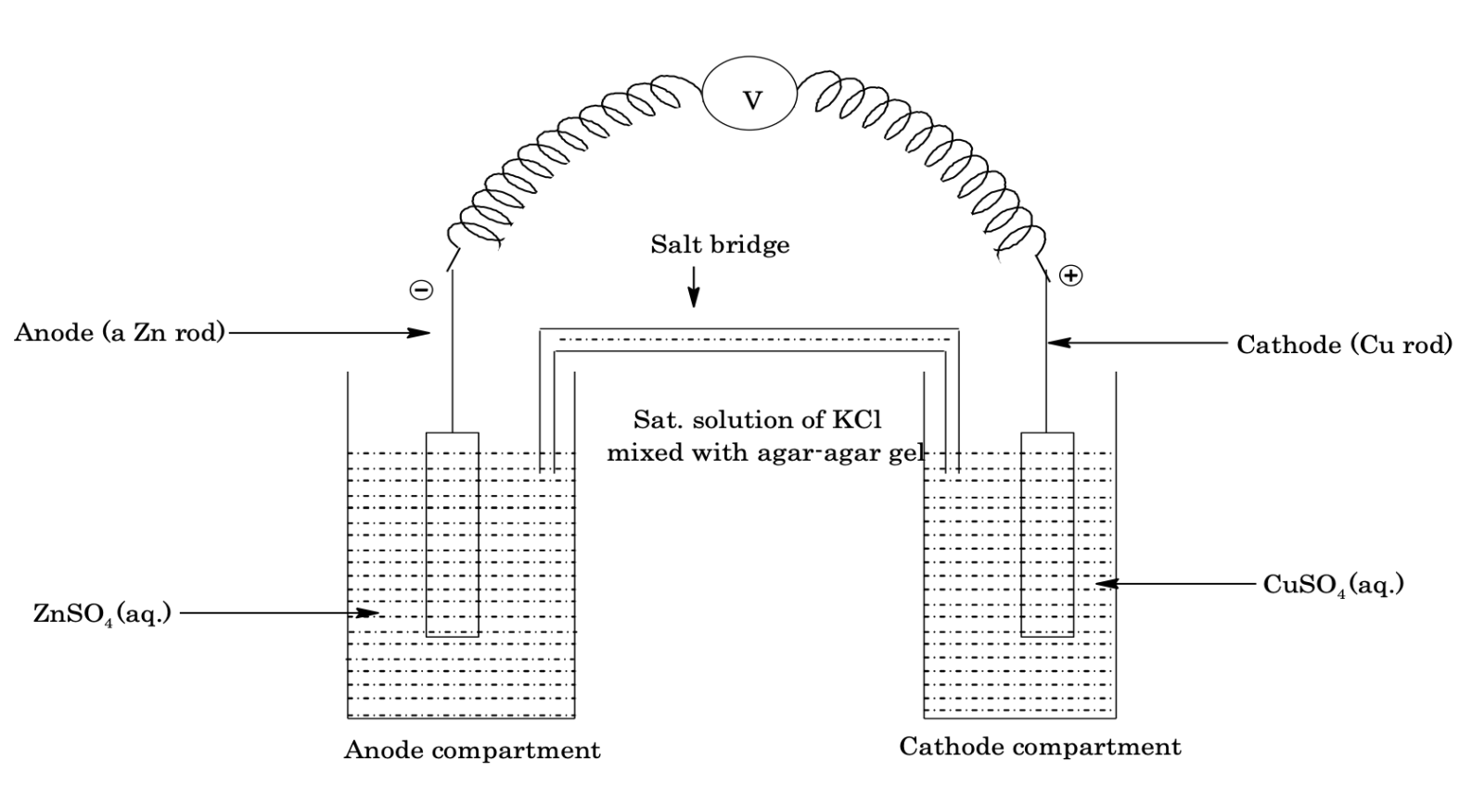
At anodes, Zn atom oxidises, into Zn²⁺ ion and loses two electrons which remain, stick with the Zn rod (that's why Zn rod is –ve) and these electrons are now pushed into the outer circuit and accepted by Cu²⁺ ion, in compartment cathode which reduces to Cu but as the cell reaction proceeds there occurs an excess of positive charge around anode and an excess of negative charge around cathode which prevents the outgoing flow of electrons and hence cell reaction stops. This problem is sort out by using a salt bridge (a glass U–tube horizontal portion of which is filled with a saturated solution of KCl and agar–agar gel) which maintain electrical neutrality in the two compartments and thus, cell reaction proceeds for a long time.

Representation of a Galvanic cell

1. When a metal rod is dipped into the solution of its own ions, for example, Zn–Cu cell.
   Anode half cell || cathode half cell, i.e.
   Zn | Zn²⁺ (g) || Cu²⁺|Cu (s)
2. When species undergoing reduction or oxidation is a gas. For example, hydrogen electrodes.
   H₂(g) → 2H⁺(aq) + 2e^-
   
   A platinum rod saturated with this gas is dipped into the solution of common ions.
   Pt_H₂ (g) | H⁺(C), when acting as anode, and
   H⁺(C) | Pt_H₂ (g), when acting as cathode
3. When species undergoing reduction or oxidation of the ions of the same metal, then again Pt – rod is used as electrodes. For example, consider the reduction half cell.

Fe³⁺ + e^- → Fe²⁺

It is represented as follows:
Pt | Fe³⁺(C₁), Fe²⁺(C₂) (as anode), and
Fe³⁺(C₁), Fe²⁺(C₂) | Pt (as cathode)

(iv) Metal–metal insoluble salt anion half cell: In such kind of half cells, a metal rod e.g. Ag rod is dipped into the solution of an electrolyte such as (KCl) saturated with a sparingly soluble salt of the same metal such as AgCl, i.e.
AgCl(s) + e^- → Ag(s) + Cl^-

It is represented as
Cl^- | AgCl(s) | Ag (As cathode), and
Ag | AgCl | Cl^- (As anode)

Example: The main function of salt bridge in Galvanic cells is

(A) To increase the conductance of solution of electrolyte in both compartments

(B) To maintain the electrical neutrality in both compartments

(C) To decrease the conductance of electrolyte solution

(D) To increase the ionic mobility

Solution: (B)

Salt bridge sends equivalent no. of counter ion in the anode and cathode compartment to maintain electrical neutrality.

ELECTRODE POTENTIAL

When a metal rod is dipped into the solution of its own ions, then a potential difference is developed between the rod and solution in contact, it is called its electrode potential. For example,

Zn(s) → Zn²⁺ + 2e⁻ , oxidation electrode potential of zinc, i.e. E_Zn/Zn²⁺, and
Cu²⁺ + 2e⁻ → Cu(s), reduction electrode potential of copper, i.e. E_Cu²⁺/Cu

Remember that for any species, E_Ox = −E_red, i.e.

It is always measured in volts.

Standard electrode potential E^°

Electrode potential of a half cell depends on the following factors:
(i) Concentration of electrolytic solution.
(ii) Temperature.
(iii) Pressure of the gas (only in the case of gaseous electrodes).

So, if the concentration of electrolyte, i.e. common ion is unity, temperature is 298 K, pressure is 1 atm, then electrode potential is called standard electrode potential (E^°).

E^°_Zn/Zn²⁺ = standard oxidation potential of zinc
E^°_Zn²⁺/Zn = standard reduction potential of zinc

Also E^°_Ox = −E^°_red

Measurement of single electrode potential

The working electrode whose electrode potential is to be measured e.g. (Zn/Zn²⁺) is coupled with some reference electrode i.e. whose E° is known such as (SHE) and then cell is completed & E_cell is measured.

Zn | Zn²⁺ || H⁺ | Pt_H2(g), E_cell is measured.

Now, E_cell = (E_red)_cathode – (E_red)_anode

E_cell = E_H⁺/H2 – E_Zn²⁺/Zn

So, E_Zn²⁺/Zn can be measured from the above equation.

Similarly, for standard electrode potential

E°_cell = (E°_red)_cathode – (E°_red)_anode

Electrochemical series

When all the species (atoms or ions) are arranged in increasing or decreasing order of their standard reduction potentials then the series thus obtained is called electrochemical series as shown below

1. The species with smaller E^o_red (i.e., more negative value) is a better reducing agent while species with higher E^o_red (i.e., more positive value) is a better oxidizing agent, e.g., E^o_red of alkali metals. For example, Li very low and that’s why these are better reducing agents.
2. A metal with low E^o_red can displace the other one with higher E^o_red from its salts, but the reverse is not true.
   e.g. Zn can displace Cu²⁺ ion, from its salts but the reverse is not true.
   Zn + CuSO₄ → ZnSO₄ + Cu(s). and Cu + ZnSO₄ → no reaction.
3. Metals above hydrogen in electrochemical series, when reacts with dil. HCl or dil. H₂SO₄, liberates H₂ gas.
   Zn + H₂SO₄ → ZnSO₄ + H₂
4. The species with higher E^o_red means it has more tendency to get reduced and the species with lower E^o_red means it has more tendency to get oxidized.

Nernst Equation

It is a mathematical expression which relates electrode potential or cell potential with the concentration of electrolyte, pressure of the gases and temperature for a half cell, e.g.

Mnⁿ⁺ + ne⁻ → M(s)

Nernst equation is written as,

E_{Mnⁿ⁺ / M} = E^o_{Mnⁿ⁺ / M} − (2.303RT / nF) log Q               …(i)

where,

• E_{Mnⁿ⁺ / M} = reduction potential of the above half cell,
• E^o_{Mnⁿ⁺ / M} = standard reduction potential of the half cell,
• R = universal gas constant ( = 8.314 J mol⁻¹ K⁻¹ )
• T = temperature in kelvin (generally, 298 K)
• n = number of moles of electrons transferred in the cell reaction.
• F = Faraday’s constant = 96500 C, Q = Reaction quotient

  = [M(s)] / [Mnⁿ⁺] = 1 / [Mnⁿ⁺]         (∴ [M(s)] = 1 M)

  E_{Mnⁿ⁺ / M} = E^o_{Mnⁿ⁺ / M} − (0.0591 / n) log (1 / [Mnⁿ⁺])

Similarly, for a complete cell, such as Zn|Zn²⁺(g) || Cu²⁺(aq)|Cu, Nernst equation is written as

E_cell = E^o_cell − (0.0591 / n) log ([Zn²⁺] / [Cu²⁺])

where,
E^o_cell = E^o_{Cu²⁺ / Cu} − E^o_{Zn²⁺ / Zn}                 …(ii)

Application of Nernst equation

1. In calculation of E_cell and E⁰_cell (as explained above).
2. In calculating the equilibrium constant of the cell reaction: When the cell reaction is at equilibrium, ΔG = 0 and hence, E_cell = 0 and Q = K_c.
   So, 0 = E⁰_cell - (0.0591/n) log K_c at 25°C
   ∴ E⁰_cell = (0.0591/n) log K_c   ...(iii)
   K_c can be calculated from equation (iii)
3. In calculating the free energy change (ΔG) of the cell reaction. It is calculated by the following equation.
   ΔG = -n F E_cell
   and ΔG = - n F E⁰_cell
   Note: EMF or E_cell is not a state function but ΔG is a state function.
4. In calculating ΔH and ΔS of the cell reaction: From Gibb’s Helmholtz equation.
   ΔG = ΔH + T (d(ΔG)/dT)_P but ΔG = - n F E_cell
   ∴ -nFE_cell = ΔH - nF T (dE_cell/dT)
   or,
   E_cell = -ΔH/nF + T (dE_cell/dT)
   or,
   ΔH = nF [ T (dE_cell/dT) - E ]
   (dE_cell/dT) is called temperature coefficient of EMF hence ΔH can be calculated from equation (iv).
   Also ΔG = ΔH - T ΔS
   So, ΔS can also be calculated from (iv)

1. In predicting the spontaneity of cell reaction
   If ΔG < 0, i.e. _Ecell > 0 then the cell reaction is spontaneous.
   If ΔG = 0, i.e. _Ecell = 0 then the cell reaction is at equilibrium.
   + If ΔG > 0, i.e. _Ecell < 0 then the cell reaction is not spontaneous.
2. In calculating the solubility and solubility product of a sparingly soluble salt.
   Ag(s) | AgCl(S) || Ag⁺ (C molar AgNO₃ sol.) | Ag(s), E_cell = xV (given)
   sat. solution
   
   E_cell = 0.00 – 0.0591/n log [Ag⁺]_anode / [Ag⁺]_cathode ...(vi)
   
   But [Ag⁺]_anode = solubility of AgCl = S and [Ag⁺]_cathode = C
   So ‘S’ can be calculated from equation (vi)
   And then, K_sp (AgCl) = [Ag⁺] [Cl^-] = S × S = S²
3. In calculating the pH of a solution in the cell. For example, consider the following half cell,
   
   H₂(g) → 2H⁺(aq) + 2e^-, E_{H⁺ / H2} = x volt
   1.0 atm
   
   ∴ pH = ( E_H⁺/H2 ) / 0.0591 ...(viii)
   
   So, pH of solution can be calculated from the above equation (viii) for this half cell.

Example: For the following two half cells Ag|AgCl, Cl⁻ (0.1M) and Ag⁺|Ag(0.1M) Which of the following statement is/are true?

(A) Eº_red for both are same

(B) E_red for both are same

(C) Eº_red & E_red are same for both cells

(D) Neither of these are same.

Solution:

(B). Since, Eº_red is the ability of a species to get reduce hence these can not be same but since electrode reactions are same so their E_red will be same.

Electrical conductance

Hindrance offered by ions present in the solution of electrolyte to the passage of charge is called electrical resistance (R). It is measured in volts.
Reciprocal of electrical resistance is called electrical conductance (C),
i.e. C = 1/R.
(units are ohm^-1 or siemen (S) or mho)

Conductivity or specific conductance κ (Kappa)

It is the conductance of the unit volume of a solution of electrolyte, i.e.
κ = 1/R × ℓ/a = C × ℓ/a
(It is measured in siemen cm^-1 or ohm^-1 cm^-1; ℓ/a is called the cell constant, where ℓ is separation between the electrodes of conductivity cell and a is the area of cross section of the electrode.
Cell constant has a unit of m^-1 or cm^-1.

Equivalent conduction H_NI

Conductance of all the ions present in a solution having one g–equivalent of the electrolyte.
Λ_eq = κ × V_eq = (κ × 1000)/N (measured in the unit of S cm².eqvt^-1)
where, V_eq = volume of solution containing 1 g equivalent of the electrolyte and κ = specific conductivity and N = Normality of electrolyte solution.

Molecular conductance H_ΛL. I

Conductance of all the ions present in a solution having 1 gm mole of the electrolyte is called molecular conductance (Λ_m).

Λ_m = κ × V_cc = (κ × 1000) / M

M = molecular mass; V = Vol. of solution containing 1 g mole of electrolyte.
It is measured in S cm² mol^-1.

Factors affecting the conductance

1. Dilution: With an increase in dilution of C, Λ_eq and Λ_m increases but κ decreases. These increase in C, Λ_eq and Λ_m with increase in dilution is due to the increase in ionic mobility (in case of strong electrolyte) while it is due to increase in number of ions and ionic mobility (in the case of weak electrolyte).
   Decrease in κ with an increase in dilution is due to the decrease in number of ions per unit volume of the solution.
2. Temperature: All kinds of conductance (C, κ, Λ_m, Λ_eq) increases with the rise of temperature due to the increase in ionic mobility.

KOHLRAUSCH LAW

It states that the total equivalent or molar conductance of an electrolyte at infinite dilution is equal to the sum of equivalent or molar conductance of its component ions at infinite dilution, i.e. λ^∞_CH3COOH is given by.

λ^∞_CH3COOH = λ^∞_CH3COO⁻ + λ^∞_H⁺
λ^∞_CaCl2 = λ^∞_Ca²⁺ + 2λ^∞_Cl⁻
λ^∞_Al2(SO4)3 = 2λ^∞_Al³⁺ + 3λ^∞_SO4²⁻

Application of Kohlrausch law

1. In calculating λ^∞ of a weak electrolytes: It is based on the fact that λ^∞ of an ion remains constant at constant temperature, no matter of which electrolyte it makes a part.
   For example: λ^∞ of CH₃COOH can be calculated as follows
   
   λ^∞_CH3COOH = λ^∞_CH3COO⁻ + λ^∞_H⁺
   = λ^∞_CH3COONa + λ^∞_Na⁺ − λ^∞_Na⁺ + λ^∞_H⁺ + λ^∞_Cl⁻ − λ^∞_Cl⁻
   ∴ λ^∞_CH3COOH = λ^∞_CH3COONa + λ^∞_HCl − λ^∞_NaCl
   
   where CH₃COONa, HCl and NaCl, all are strong electrolytes and their λ^∞ can be measured in laboratory.
2. In calculating the degree of ionization of a weak electrolyte: Degree of ionization of weak electrolyte (α) is by given by the following expression:
   
   α = λ_v / λ^∞
   
   Where λ = (κ × 1000) / N, and λ^∞ is calculated from Kohlrausch law as explained in application (i).
3. In calculating the solubility (S) and solubility product (K_sp) of sparingly soluble salts: Suppose we want to measure solubility of BaSO₄ then we prepare a saturated solution of it and measure its conductivity (κ).
   
   Now, λ^∞_m = λ^∞_v for a sparingly soluble salt = (κ × 1000) / M
   
   Molar concentration = M = solubility of BaSO₄ can be calculated.
   Then K_sp = [Ba²⁺][SO₄²⁻] = S²
   Hence, K_sp can also be calculated.

Solved Example

1. Standard reduction potential (E^o) for OCl⁻/Cl⁻ and Cl⁻/½Cl₂ are 0.94 V and −1.36 V respectively. The E^o value of OCl⁻/Cl₂ will be

(A) −0.42 V

(B) −2.20 V

(C) 0.52 V

(D) 1.04 V

Sol. (A).

(I) OCl⁻ + 2e⁻ → Cl⁻, E^o₁ = 0.94 V

(II) ½Cl₂ + e⁻ → Cl⁻, E^o₂ = −1.36 V

(III) OCl⁻ + e⁻ → ½Cl₂, E^o₃ = ?

Now, III = I − II

∴ ΔG^o₃ = ΔG^o₁ − ΔG^o₂, but E^o₃ ≠ E^o₁ − E^o₂ (∴ E is not a state function.)

or, −n₃FE^o₃ = −n₁FE^o₁ − (n₂FE^o₂)

∴ E^o₃ = (n₁E^o₁ − n₂E^o₂) / n₃

2. When Zn is added to CuSO₄ solution, copper is precipitated because of

(A) Reduction of Zn

(B) Hydrolysis of CuSO₄

(C) Oxidation of Zn

(D) Reduction of SO₄²⁻ ions

Sol. (C).

 Reduction
Zn(s) + CuSO4 → ZnSO4 + Cu(s)
Oxidation
 

3. Saturated solution of KNO₃ is used to make ‘salt bridge’ because

(A) Velocity of K⁺ is greater than that of NO₃⁻

(B) Velocity of NO₃⁻ is greater than that of K⁺

(C) Velocity of both K⁺ and NO₃⁻ are nearly the same.

(D) KNO₃ is highly soluble in water.

Sol. (C).

Salts having greater mobilities are used in salt bridge.

4. When a rod of metal ‘A’ is dipped in an aqueous solution of metal ‘B’ (conc. of B²⁺ being 1.0 M) at 25^oC, the standard electrode potentials are A²⁺/A = – 0.76 V and B²⁺/B = 0.34 V.

(A) ‘A’ will gradually dissolve.

(B) B will deposit on A

(C) No reaction will occur

(D) water will decompose into H₂ and O₂

Sol. (A).

Since E^o_A²⁺/A < E^o_B²⁺/B, hence A is oxidized & B is reduced, i.e., A will dissolve in the solution