A solid–liquid solution can be ideal or non-ideal depending on the nature of interactions between the solute and solvent molecules compared to those in the pure components. The classification follows the same physical chemistry principles applied to liquid–liquid solutions, but with one component in the solid state before dissolution. Ideal solid–liquid solutions An ideal solid–liquid solution is one where: The intermolecular forces between solute–solvent particles are equal in strength to those between solvent–solvent and solute–solute particles. Enthalpy of mixing (ΔHmix) = 0 – No heat is absorbed or released when the solute dissolves. Volume change on mixing (ΔVmix) = 0 – The total volume is simply the sum of the volumes of solute and solvent. Obeys Raoult’s Law over the entire concentration range. Example: Dissolving a non-reactive solid like benzene’s solid derivatives into a chemically similar organic solvent at a molecular level. However, in practice, truly ideal solid–liquid solutions are rare. Non-ideal solid–liquid solutions Most real-world solid–liquid solutions are non-ideal because the interactions between solute and solvent differ in strength from those in the pure components. Positive deviation from Raoult’s Law – Solute–solvent forces are weaker than like–like forces; dissolution is endothermic (e.g., dissolving certain salts where lattice energy is high). Negative deviation – Solute–solvent forces are stronger, causing exothermic dissolution (e.g., dissolving NaOH pellets in water releases significant heat). Practical relevance: In pharmaceuticals, predicting whether a drug in a liquid medium behaves ideally affects solubility, stability, and shelf life. In food science, non-ideal effects influence texture, sweetness perception, and crystallization. In chemical manufacturing, deviations from ideality determine energy requirements for mixing and crystallization. Key takeaway: While the concept of ideal solutions provides a useful theoretical framework, solid–liquid solutions are usually non-ideal in real applications due to differences in bonding, polarity, and molecular size between the solute and solvent.

A solid–liquid solution can be ideal or non-ideal depending on the nature of interactions between the solute and solvent molecules compared to those in the pure components. The classification follows the same physical chemistry principles applied to liquid–liquid solutions, but with one component in the solid state before dissolution. Ideal solid–liquid solutions An ideal solid–liquid solution is one where: The intermolecular forces between solute–solvent particles are equal in strength to those between solvent–solvent and solute–solute particles. Enthalpy of mixing (ΔHmix) = 0 – No heat is absorbed or released when the solute dissolves. Volume change on mixing (ΔVmix) = 0 – The total volume is simply the sum of the volumes of solute and solvent. Obeys Raoult’s Law over the entire concentration range. Example: Dissolving a non-reactive solid like benzene’s solid derivatives into a chemically similar organic solvent at a molecular level. However, in practice, truly ideal solid–liquid solutions are rare. Non-ideal solid–liquid solutions Most real-world solid–liquid solutions are non-ideal because the interactions between solute and solvent differ in strength from those in the pure components. Positive deviation from Raoult’s Law – Solute–solvent forces are weaker than like–like forces; dissolution is endothermic (e.g., dissolving certain salts where lattice energy is high). Negative deviation – Solute–solvent forces are stronger, causing exothermic dissolution (e.g., dissolving NaOH pellets in water releases significant heat). Practical relevance: In pharmaceuticals, predicting whether a drug in a liquid medium behaves ideally affects solubility, stability, and shelf life. In food science, non-ideal effects influence texture, sweetness perception, and crystallization. In chemical manufacturing, deviations from ideality determine energy requirements for mixing and crystallization. Key takeaway: While the concept of ideal solutions provides a useful theoretical framework, solid–liquid solutions are usually non-ideal in real applications due to differences in bonding, polarity, and molecular size between the solute and solvent.

A solid dissolved in a liquid forms a solid–liquid solution, one of the most common and useful types of mixtures in everyday life, laboratories, and industrial applications. In these solutions, solid particles break down to the molecular or ionic level and disperse evenly throughout the liquid solvent, creating a stable, homogeneous mixture. Everyday examples: Table salt (NaCl) in water – Common in cooking, food preservation, and medical saline solutions. Sugar in water – Used in beverages, syrups, and desserts, where hydrogen bonding between sugar and water ensures complete dissolution. Instant coffee powder in hot water – Creates a uniform beverage with dissolved coffee solids. Industrial and laboratory examples: Copper sulfate in water – Produces a blue solution used in agriculture, electroplating, and chemistry experiments. Potassium permanganate in water – Forms a purple solution for disinfecting and oxidation reactions. Fertilizers in irrigation water – Solid nutrient salts like urea and ammonium nitrate dissolved to feed crops efficiently. Pharmaceutical examples: Vitamin C (ascorbic acid) in water – For nutritional supplements and immune support. Oral rehydration salts (ORS) – A blend of electrolytes and glucose dissolved in water to treat dehydration. Key characteristics of these solutions: Uniform appearance with no visible particles. Stability over time without sedimentation under normal conditions. Solute cannot be separated by ordinary filtration. Applications: Solid–liquid solutions are essential in food processing, pharmaceuticals, water treatment, and chemical manufacturing because they allow precise dosing, fast chemical reactions, and easy transport of dissolved materials.

A solid dissolved in a liquid forms a solid–liquid solution, one of the most common and useful types of mixtures in everyday life, laboratories, and industrial applications. In these solutions, solid particles break down to the molecular or ionic level and disperse evenly throughout the liquid solvent, creating a stable, homogeneous mixture. Everyday examples: Table salt (NaCl) in water – Common in cooking, food preservation, and medical saline solutions. Sugar in water – Used in beverages, syrups, and desserts, where hydrogen bonding between sugar and water ensures complete dissolution. Instant coffee powder in hot water – Creates a uniform beverage with dissolved coffee solids. Industrial and laboratory examples: Copper sulfate in water – Produces a blue solution used in agriculture, electroplating, and chemistry experiments. Potassium permanganate in water – Forms a purple solution for disinfecting and oxidation reactions. Fertilizers in irrigation water – Solid nutrient salts like urea and ammonium nitrate dissolved to feed crops efficiently. Pharmaceutical examples: Vitamin C (ascorbic acid) in water – For nutritional supplements and immune support. Oral rehydration salts (ORS) – A blend of electrolytes and glucose dissolved in water to treat dehydration. Key characteristics of these solutions: Uniform appearance with no visible particles. Stability over time without sedimentation under normal conditions. Solute cannot be separated by ordinary filtration. Applications: Solid–liquid solutions are essential in food processing, pharmaceuticals, water treatment, and chemical manufacturing because they allow precise dosing, fast chemical reactions, and easy transport of dissolved materials.

Not all liquids are effective solvents under all conditions, but every liquid has the potential to dissolve something even if only in trace amounts. A solvent is defined as a substance, typically in greater quantity, that dissolves a solute to form a homogeneous solution. Whether a liquid can act as a solvent depends on its molecular structure, polarity, intermolecular forces, and the properties of the solute. Why most liquids can dissolve something: Molecular interactions – All liquids exhibit some form of intermolecular attraction (van der Waals forces, dipole–dipole interactions, hydrogen bonding), which can interact with other molecules. “Like dissolves like” principle – Polar liquids dissolve polar or ionic solutes well (e.g., water dissolving salt), and non-polar liquids dissolve non-polar solutes (e.g., hexane dissolving oil). Temperature effects – Increasing temperature often increases solubility for many solutes in liquids. Examples of liquids as solvents: Water – Dissolves salts, sugars, acids, and gases like oxygen and carbon dioxide; often called the “universal solvent” because of its high polarity and hydrogen-bonding ability. Ethanol – Dissolves both polar and some non-polar substances, making it valuable in pharmaceuticals and cosmetics. Liquid metals – Mercury dissolves certain metals to form amalgams. Oils – Act as solvents for fat-soluble vitamins and many non-polar compounds. Exceptions and limitations: Some liquids may have extremely low solvent capacity for certain solutes due to incompatible molecular forces. For example: Liquid nitrogen at cryogenic temperatures is a poor solvent for most substances due to extremely low kinetic energy of molecules. Pure liquid hydrogen is non-polar and dissolves very few substances outside its molecular similarity. While all liquids can technically act as a solvent for something, their effectiveness varies drastically. The choice of solvent in industry and research depends on chemical compatibility, safety, cost, and the desired physical or chemical properties of the resulting solution.

Not all liquids are effective solvents under all conditions, but every liquid has the potential to dissolve something even if only in trace amounts. A solvent is defined as a substance, typically in greater quantity, that dissolves a solute to form a homogeneous solution. Whether a liquid can act as a solvent depends on its molecular structure, polarity, intermolecular forces, and the properties of the solute. Why most liquids can dissolve something: Molecular interactions – All liquids exhibit some form of intermolecular attraction (van der Waals forces, dipole–dipole interactions, hydrogen bonding), which can interact with other molecules. “Like dissolves like” principle – Polar liquids dissolve polar or ionic solutes well (e.g., water dissolving salt), and non-polar liquids dissolve non-polar solutes (e.g., hexane dissolving oil). Temperature effects – Increasing temperature often increases solubility for many solutes in liquids. Examples of liquids as solvents: Water – Dissolves salts, sugars, acids, and gases like oxygen and carbon dioxide; often called the “universal solvent” because of its high polarity and hydrogen-bonding ability. Ethanol – Dissolves both polar and some non-polar substances, making it valuable in pharmaceuticals and cosmetics. Liquid metals – Mercury dissolves certain metals to form amalgams. Oils – Act as solvents for fat-soluble vitamins and many non-polar compounds. Exceptions and limitations: Some liquids may have extremely low solvent capacity for certain solutes due to incompatible molecular forces. For example: Liquid nitrogen at cryogenic temperatures is a poor solvent for most substances due to extremely low kinetic energy of molecules. Pure liquid hydrogen is non-polar and dissolves very few substances outside its molecular similarity. While all liquids can technically act as a solvent for something, their effectiveness varies drastically. The choice of solvent in industry and research depends on chemical compatibility, safety, cost, and the desired physical or chemical properties of the resulting solution.

Solutions are not always liquid because the defining feature of a solution is homogeneity at the molecular level, not the physical state of the solvent. The phase of the solvent determines the overall phase of the solution, and solvents can be solid, liquid, or gas. This means solutions can exist in all three states of matter, depending on the combination of solute and solvent. Examples by state: 1. Solid Solutions Solvent phase : Solid Examples : Brass (zinc dissolved in copper) – a uniform metal alloy. Stainless steel (carbon and chromium dissolved in iron). Doped silicon in electronics (phosphorus or boron in a silicon crystal lattice). 2. Liquid Solutions Solvent phase : Liquid Examples : Saltwater (NaCl dissolved in water). Ethanol in water (alcoholic beverages). Carbon dioxide in soda. 3. Gas Solutions Solvent phase : Gas Examples : Air (oxygen, carbon dioxide, and trace gases in nitrogen). Natural gas mixtures (methane with other hydrocarbons). Why people often think solutions are only liquids Liquid solutions are the most visible and commonly used in everyday life—beverages, medicines, cleaning agents—so many assume the term “solution” refers only to liquids. However, in chemistry, the term is broader and applies to any homogeneous mixture, regardless of phase. Importance of recognizing all types In materials science, solid solutions are critical for designing alloys with specific mechanical properties. In environmental science, gas solutions are vital for understanding air composition and gas exchange with oceans. In food technology, both liquid and gas solutions influence flavor, texture, and preservation.

Solutions are not always liquid because the defining feature of a solution is homogeneity at the molecular level, not the physical state of the solvent. The phase of the solvent determines the overall phase of the solution, and solvents can be solid, liquid, or gas. This means solutions can exist in all three states of matter, depending on the combination of solute and solvent. Examples by state: 1. Solid Solutions Solvent phase : Solid Examples : Brass (zinc dissolved in copper) – a uniform metal alloy. Stainless steel (carbon and chromium dissolved in iron). Doped silicon in electronics (phosphorus or boron in a silicon crystal lattice). 2. Liquid Solutions Solvent phase : Liquid Examples : Saltwater (NaCl dissolved in water). Ethanol in water (alcoholic beverages). Carbon dioxide in soda. 3. Gas Solutions Solvent phase : Gas Examples : Air (oxygen, carbon dioxide, and trace gases in nitrogen). Natural gas mixtures (methane with other hydrocarbons). Why people often think solutions are only liquids Liquid solutions are the most visible and commonly used in everyday life—beverages, medicines, cleaning agents—so many assume the term “solution” refers only to liquids. However, in chemistry, the term is broader and applies to any homogeneous mixture, regardless of phase. Importance of recognizing all types In materials science, solid solutions are critical for designing alloys with specific mechanical properties. In environmental science, gas solutions are vital for understanding air composition and gas exchange with oceans. In food technology, both liquid and gas solutions influence flavor, texture, and preservation.

A gas solution in liquid is a homogeneous mixture where the solvent is a liquid and the solute is a gas. In these systems, gas molecules are dispersed at the molecular level within the liquid, resulting in a single-phase solution with uniform properties. The solubility of gases in liquids depends heavily on temperature, pressure, and the chemical nature of both the gas and the liquid. Key examples: Carbonated beverages – Carbon dioxide dissolved in water or flavored drinks under high pressure. Upon opening the container, the pressure drops, causing CO₂ to escape as bubbles. Oxygen in water – Naturally occurs in rivers, lakes, and oceans, essential for aquatic life. Dissolved oxygen levels are a key water quality indicator. Nitrogen in beer (Nitro brews) – Gives certain beers a smoother texture and creamier foam. Chlorine in water – Used in municipal water treatment for disinfection purposes. Ammonia solution – Ammonia gas dissolved in water, used in household cleaners and industrial processes. Anesthetic gases in blood – In medical contexts, inhaled anesthetics dissolve in the blood and tissues during surgery. Important factors influencing gas solubility: Temperature – For most gases, solubility decreases as temperature increases. Pressure – Solubility increases with pressure, following Henry’s Law. Nature of the gas and liquid – Polar liquids like water dissolve polar gases (e.g., ammonia) better than non-polar gases. Applications: Food and beverage industry – Carbonated drinks, sparkling wines, and nitrogen-infused beverages. Environmental science – Studying dissolved oxygen and carbon dioxide levels in aquatic ecosystems. Medicine – Oxygen therapy and anesthesia delivery.

A gas solution in liquid is a homogeneous mixture where the solvent is a liquid and the solute is a gas. In these systems, gas molecules are dispersed at the molecular level within the liquid, resulting in a single-phase solution with uniform properties. The solubility of gases in liquids depends heavily on temperature, pressure, and the chemical nature of both the gas and the liquid. Key examples: Carbonated beverages – Carbon dioxide dissolved in water or flavored drinks under high pressure. Upon opening the container, the pressure drops, causing CO₂ to escape as bubbles. Oxygen in water – Naturally occurs in rivers, lakes, and oceans, essential for aquatic life. Dissolved oxygen levels are a key water quality indicator. Nitrogen in beer (Nitro brews) – Gives certain beers a smoother texture and creamier foam. Chlorine in water – Used in municipal water treatment for disinfection purposes. Ammonia solution – Ammonia gas dissolved in water, used in household cleaners and industrial processes. Anesthetic gases in blood – In medical contexts, inhaled anesthetics dissolve in the blood and tissues during surgery. Important factors influencing gas solubility: Temperature – For most gases, solubility decreases as temperature increases. Pressure – Solubility increases with pressure, following Henry’s Law. Nature of the gas and liquid – Polar liquids like water dissolve polar gases (e.g., ammonia) better than non-polar gases. Applications: Food and beverage industry – Carbonated drinks, sparkling wines, and nitrogen-infused beverages. Environmental science – Studying dissolved oxygen and carbon dioxide levels in aquatic ecosystems. Medicine – Oxygen therapy and anesthesia delivery.

Solutions can be classified in multiple ways by the physical state of the solvent, by the nature of the solute and solvent, or by their behavior in relation to ideality. The most common and practical classification is based on the state of the solvent, which determines the overall phase of the solution. 1. Gaseous Solutions Solvent phase : Gas Possible solutes : Gas, liquid, or solid (though solids in gases are rare under normal conditions). Examples : Gas in gas – Air (oxygen, CO₂, and trace gases in nitrogen). Liquid in gas – Water vapor in air (humidity). Solid in gas – Smoke (solid particles in air; technically a colloid, not a true solution). 2. Liquid Solutions Solvent phase : Liquid Possible solutes : Solid, liquid, or gas. Examples : Solid in liquid – Saltwater (NaCl in water), sugar syrup. Liquid in liquid – Ethanol in water, acetic acid in water (vinegar). Gas in liquid – Carbon dioxide in soda, oxygen in water. 3. Solid Solutions Solvent phase : Solid Possible solutes : Solid, liquid, or gas. Examples : Solid in solid – Alloys like brass (zinc in copper) and bronze (tin in copper). Gas in solid – Hydrogen in palladium (used for hydrogen storage). Liquid in solid – Amalgams where mercury is dispersed in another metal. Other classifications: Based on concentration : Dilute vs. concentrated solutions. Based on ideality : Ideal solutions (obey Raoult’s Law exactly) vs. non-ideal solutions (show deviations). Based on miscibility : Miscible vs. immiscible liquid pairs. Why classification matters: In chemistry, understanding the type of solution is critical for predicting properties like boiling point, freezing point, and vapor pressure. In industry, it helps choose the correct mixing process, storage method, and application.

Solutions can be classified in multiple ways by the physical state of the solvent, by the nature of the solute and solvent, or by their behavior in relation to ideality. The most common and practical classification is based on the state of the solvent, which determines the overall phase of the solution. 1. Gaseous Solutions Solvent phase : Gas Possible solutes : Gas, liquid, or solid (though solids in gases are rare under normal conditions). Examples : Gas in gas – Air (oxygen, CO₂, and trace gases in nitrogen). Liquid in gas – Water vapor in air (humidity). Solid in gas – Smoke (solid particles in air; technically a colloid, not a true solution). 2. Liquid Solutions Solvent phase : Liquid Possible solutes : Solid, liquid, or gas. Examples : Solid in liquid – Saltwater (NaCl in water), sugar syrup. Liquid in liquid – Ethanol in water, acetic acid in water (vinegar). Gas in liquid – Carbon dioxide in soda, oxygen in water. 3. Solid Solutions Solvent phase : Solid Possible solutes : Solid, liquid, or gas. Examples : Solid in solid – Alloys like brass (zinc in copper) and bronze (tin in copper). Gas in solid – Hydrogen in palladium (used for hydrogen storage). Liquid in solid – Amalgams where mercury is dispersed in another metal. Other classifications: Based on concentration : Dilute vs. concentrated solutions. Based on ideality : Ideal solutions (obey Raoult’s Law exactly) vs. non-ideal solutions (show deviations). Based on miscibility : Miscible vs. immiscible liquid pairs. Why classification matters: In chemistry, understanding the type of solution is critical for predicting properties like boiling point, freezing point, and vapor pressure. In industry, it helps choose the correct mixing process, storage method, and application.

A solution in which both the solute and solvent are in the same physical state is referred to as a homogeneous phase solution. The phase is determined by the solvent, but in these cases, the solute shares the same state, making the mixture more uniform in molecular structure and interaction.When both are in the same phase, molecular compatibility tends to be high because the intermolecular forces between solute and solvent molecules are often similar. This follows the “like dissolves like” principle, meaning substances with similar polarity and bonding types tend to mix well. Examples across phases: 1. Gas in Gas (Gaseous solution) Air – Oxygen (solute) uniformly mixed in nitrogen (solvent). Natural gas blends – Methane with smaller amounts of ethane and propane. 2. Liquid in Liquid (Liquid–liquid solution) Ethanol in water – Found in alcoholic beverages and antiseptics. Acetic acid in water – Found in vinegar. Glycerin in water – Used in pharmaceuticals and cosmetics. 3. Solid in Solid (Solid solution) Brass – Zinc dissolved in copper. Stainless steel – Carbon and chromium dissolved in iron. Alloys in jewelry – Gold mixed with copper or silver. Key points: The solvent determines the phase of the solution, even if the solute starts in a different phase before dissolving. Same-phase solutions often have no phase boundaries or immiscibility issues, leading to long-term stability. These solutions are widely used in metallurgy, chemical manufacturing, pharmaceutical formulation, and gas supply systems.

A solution in which both the solute and solvent are in the same physical state is referred to as a homogeneous phase solution. The phase is determined by the solvent, but in these cases, the solute shares the same state, making the mixture more uniform in molecular structure and interaction.When both are in the same phase, molecular compatibility tends to be high because the intermolecular forces between solute and solvent molecules are often similar. This follows the “like dissolves like” principle, meaning substances with similar polarity and bonding types tend to mix well. Examples across phases: 1. Gas in Gas (Gaseous solution) Air – Oxygen (solute) uniformly mixed in nitrogen (solvent). Natural gas blends – Methane with smaller amounts of ethane and propane. 2. Liquid in Liquid (Liquid–liquid solution) Ethanol in water – Found in alcoholic beverages and antiseptics. Acetic acid in water – Found in vinegar. Glycerin in water – Used in pharmaceuticals and cosmetics. 3. Solid in Solid (Solid solution) Brass – Zinc dissolved in copper. Stainless steel – Carbon and chromium dissolved in iron. Alloys in jewelry – Gold mixed with copper or silver. Key points: The solvent determines the phase of the solution, even if the solute starts in a different phase before dissolving. Same-phase solutions often have no phase boundaries or immiscibility issues, leading to long-term stability. These solutions are widely used in metallurgy, chemical manufacturing, pharmaceutical formulation, and gas supply systems.

A liquid gas solution is a type of homogeneous mixture where the solvent is a liquid and the solute is a gas. In such solutions, gas molecules are dispersed at the molecular level within the liquid, forming a single-phase system that appears uniform throughout. Because gases are compressible and have low solubility compared to solids or liquids, their ability to dissolve in a liquid depends heavily on factors like temperature, pressure, and the nature of both the gas and solvent. Key characteristics: Gas solubility in liquids generally increases with pressure (Henry’s Law). Gas solubility decreases with temperature for most gases—explaining why carbonated drinks go flat faster when warm. The interaction between the gas and the liquid determines miscibility; polar liquids like water tend to dissolve polar or reactive gases more readily. Examples: Carbonated beverages – Carbon dioxide dissolved in water or flavored drinks under high pressure, giving them their fizz. Oxygenated water – Water enriched with dissolved oxygen for aquaculture or therapeutic uses. Ammonia solution – Ammonia gas dissolved in water, forming a commonly used cleaning and industrial agent. Chlorinated water – Chlorine gas dissolved in water for disinfection in swimming pools or municipal supplies. Soda water – Plain water with dissolved CO₂ under pressure. Applications: Food & beverage industry – Soft drinks, beer, and sparkling wines rely on liquid–gas solutions for taste and texture. Medical field – Oxygenated liquids are studied for potential use in supporting breathing during respiratory distress. Environmental processes – Dissolved gases like oxygen and carbon dioxide are critical for aquatic life and water quality monitoring.

A liquid gas solution is a type of homogeneous mixture where the solvent is a liquid and the solute is a gas. In such solutions, gas molecules are dispersed at the molecular level within the liquid, forming a single-phase system that appears uniform throughout. Because gases are compressible and have low solubility compared to solids or liquids, their ability to dissolve in a liquid depends heavily on factors like temperature, pressure, and the nature of both the gas and solvent. Key characteristics: Gas solubility in liquids generally increases with pressure (Henry’s Law). Gas solubility decreases with temperature for most gases—explaining why carbonated drinks go flat faster when warm. The interaction between the gas and the liquid determines miscibility; polar liquids like water tend to dissolve polar or reactive gases more readily. Examples: Carbonated beverages – Carbon dioxide dissolved in water or flavored drinks under high pressure, giving them their fizz. Oxygenated water – Water enriched with dissolved oxygen for aquaculture or therapeutic uses. Ammonia solution – Ammonia gas dissolved in water, forming a commonly used cleaning and industrial agent. Chlorinated water – Chlorine gas dissolved in water for disinfection in swimming pools or municipal supplies. Soda water – Plain water with dissolved CO₂ under pressure. Applications: Food & beverage industry – Soft drinks, beer, and sparkling wines rely on liquid–gas solutions for taste and texture. Medical field – Oxygenated liquids are studied for potential use in supporting breathing during respiratory distress. Environmental processes – Dissolved gases like oxygen and carbon dioxide are critical for aquatic life and water quality monitoring.

No not all solutions are liquids. While liquid solutions are the most familiar in everyday life, solutions can exist in any state of matter solid, liquid, or gas—depending on the phase of the solvent, which determines the overall phase of the solution. 1. Solid Solutions In these, the solvent is solid, and the solute can be solid, liquid, or gas. Examples: Alloys – Brass (zinc dissolved in copper), bronze (tin dissolved in copper). Doped semiconductors – Silicon with phosphorus or boron atoms uniformly dispersed for electronics. Gemstones – Some colored crystals, like ruby, are corundum with trace chromium impurities. 2. Liquid Solutions In these, the solvent is liquid, and the solute can be solid, liquid, or gas. Examples: Solid in liquid – Saltwater (NaCl in water). Liquid in liquid – Ethanol in water. Gas in liquid – Carbon dioxide in soda. 3. Gas Solutions In these, the solvent is gas, and the solute can be gas, liquid, or (in rare cases) solid. Examples: Gas in gas – Air (oxygen, carbon dioxide, and trace gases in nitrogen). Natural gas mixtures – Methane with other hydrocarbons. Breathing gas mixtures – Oxygen–helium blends for deep-sea diving. Key takeaway: The defining feature of a solution is homogeneity at the molecular level , not whether it is liquid. A solid, liquid, or gas can act as the solvent, and the solute can be in any phase before mixing. Why this matters: Understanding that solutions are not limited to liquids is essential in fields like metallurgy (solid solutions), environmental science (gas solutions in air), and pharmaceuticals (solid drug dispersions). It broadens the scope of chemistry beyond just liquid mixtures and allows for more accurate classification and application.

No not all solutions are liquids. While liquid solutions are the most familiar in everyday life, solutions can exist in any state of matter solid, liquid, or gas—depending on the phase of the solvent, which determines the overall phase of the solution. 1. Solid Solutions In these, the solvent is solid, and the solute can be solid, liquid, or gas. Examples: Alloys – Brass (zinc dissolved in copper), bronze (tin dissolved in copper). Doped semiconductors – Silicon with phosphorus or boron atoms uniformly dispersed for electronics. Gemstones – Some colored crystals, like ruby, are corundum with trace chromium impurities. 2. Liquid Solutions In these, the solvent is liquid, and the solute can be solid, liquid, or gas. Examples: Solid in liquid – Saltwater (NaCl in water). Liquid in liquid – Ethanol in water. Gas in liquid – Carbon dioxide in soda. 3. Gas Solutions In these, the solvent is gas, and the solute can be gas, liquid, or (in rare cases) solid. Examples: Gas in gas – Air (oxygen, carbon dioxide, and trace gases in nitrogen). Natural gas mixtures – Methane with other hydrocarbons. Breathing gas mixtures – Oxygen–helium blends for deep-sea diving. Key takeaway: The defining feature of a solution is homogeneity at the molecular level , not whether it is liquid. A solid, liquid, or gas can act as the solvent, and the solute can be in any phase before mixing. Why this matters: Understanding that solutions are not limited to liquids is essential in fields like metallurgy (solid solutions), environmental science (gas solutions in air), and pharmaceuticals (solid drug dispersions). It broadens the scope of chemistry beyond just liquid mixtures and allows for more accurate classification and application.

A solid in liquid solution is a homogeneous mixture in which a solid solute is completely dissolved in a liquid solvent at the molecular or ionic level. The resulting solution has a single uniform phase with no visible particles, sedimentation, or separation. This type of solution is extremely common in both everyday life and industrial processes. Common examples in daily life: Salt in water – Sodium chloride dissolves completely in water, forming a saline solution used in cooking, food preservation, and medical treatments like IV drips. Sugar in water – A staple in beverages, syrups, and confectionery, where sugar’s hydrogen bonds interact strongly with water molecules. Instant coffee in water – A mix of solid coffee powder and water, producing a uniform beverage. Laboratory and industrial examples: Copper sulfate in water – Produces a bright blue solution used in electroplating, agriculture, and chemistry experiments. Potassium permanganate in water – Creates a purple solution used in water purification and as an oxidizing agent. Fertilizers in irrigation water – Solid nutrient salts like ammonium nitrate dissolved in water for agricultural use. Pharmaceutical examples: Vitamin C (ascorbic acid) in water – Used in supplements and medical preparations for quick absorption. Oral rehydration salts (ORS) – A combination of electrolytes and glucose dissolved in water to treat dehydration. Key characteristics of these solutions: Uniform composition throughout. Cannot be separated by ordinary filtration. Stable without particle settling under normal storage conditions. Why they matter: Solid–liquid solutions are essential for nutrient delivery , chemical processing , pharmaceutical dosing , and water treatment . Their predictable stability and ease of preparation make them one of the most widely used solution types worldwide.

A solid in liquid solution is a homogeneous mixture in which a solid solute is completely dissolved in a liquid solvent at the molecular or ionic level. The resulting solution has a single uniform phase with no visible particles, sedimentation, or separation. This type of solution is extremely common in both everyday life and industrial processes. Common examples in daily life: Salt in water – Sodium chloride dissolves completely in water, forming a saline solution used in cooking, food preservation, and medical treatments like IV drips. Sugar in water – A staple in beverages, syrups, and confectionery, where sugar’s hydrogen bonds interact strongly with water molecules. Instant coffee in water – A mix of solid coffee powder and water, producing a uniform beverage. Laboratory and industrial examples: Copper sulfate in water – Produces a bright blue solution used in electroplating, agriculture, and chemistry experiments. Potassium permanganate in water – Creates a purple solution used in water purification and as an oxidizing agent. Fertilizers in irrigation water – Solid nutrient salts like ammonium nitrate dissolved in water for agricultural use. Pharmaceutical examples: Vitamin C (ascorbic acid) in water – Used in supplements and medical preparations for quick absorption. Oral rehydration salts (ORS) – A combination of electrolytes and glucose dissolved in water to treat dehydration. Key characteristics of these solutions: Uniform composition throughout. Cannot be separated by ordinary filtration. Stable without particle settling under normal storage conditions. Why they matter: Solid–liquid solutions are essential for nutrient delivery , chemical processing , pharmaceutical dosing , and water treatment . Their predictable stability and ease of preparation make them one of the most widely used solution types worldwide.

All liquid solutions share certain defining properties that make them distinct from other mixtures like suspensions or colloids. These properties arise from the fact that the solute is dispersed at the molecular or ionic level within a liquid solvent, creating a stable and homogeneous system. 1. Homogeneity A liquid solution has the same composition and appearance throughout. Whether you take a sample from the top, middle, or bottom, the ratio of solute to solvent remains constant. This is due to the uniform molecular-level distribution of particles. 2. Stability Once formed, a liquid solution does not separate into layers or cause the solute to settle over time under normal conditions. This stability makes solutions ideal for storage and transport in industries like pharmaceuticals and food. 3. Transparency Most liquid solutions are transparent (though they can be colored if the solute or solvent has a natural color). They do not scatter light, which differentiates them from colloids that exhibit the Tyndall effect. 4. Particle size The solute particles are extremely small—generally less than 1 nanometer which ensures they cannot be filtered out by normal filter paper. 5. Consistent properties Physical properties like boiling point, freezing point, density, and vapor pressure are uniform throughout the solution and change predictably with concentration, following established chemical laws such as Raoult’s Law and colligative property principles. 6. Non-settling nature Unlike suspensions, the dissolved particles in a liquid solution remain dispersed indefinitely without agitation. Examples demonstrating these properties: Saltwater – clear, stable, and uniform. Ethanol–water mixtures – transparent and homogeneous. Sugar syrups – viscous yet uniform and stable. Why it matters: Recognizing these properties helps in quality control, formulation stability testing, and determining whether a mixture truly qualifies as a solution in scientific and industrial contexts.

All liquid solutions share certain defining properties that make them distinct from other mixtures like suspensions or colloids. These properties arise from the fact that the solute is dispersed at the molecular or ionic level within a liquid solvent, creating a stable and homogeneous system. 1. Homogeneity A liquid solution has the same composition and appearance throughout. Whether you take a sample from the top, middle, or bottom, the ratio of solute to solvent remains constant. This is due to the uniform molecular-level distribution of particles. 2. Stability Once formed, a liquid solution does not separate into layers or cause the solute to settle over time under normal conditions. This stability makes solutions ideal for storage and transport in industries like pharmaceuticals and food. 3. Transparency Most liquid solutions are transparent (though they can be colored if the solute or solvent has a natural color). They do not scatter light, which differentiates them from colloids that exhibit the Tyndall effect. 4. Particle size The solute particles are extremely small—generally less than 1 nanometer which ensures they cannot be filtered out by normal filter paper. 5. Consistent properties Physical properties like boiling point, freezing point, density, and vapor pressure are uniform throughout the solution and change predictably with concentration, following established chemical laws such as Raoult’s Law and colligative property principles. 6. Non-settling nature Unlike suspensions, the dissolved particles in a liquid solution remain dispersed indefinitely without agitation. Examples demonstrating these properties: Saltwater – clear, stable, and uniform. Ethanol–water mixtures – transparent and homogeneous. Sugar syrups – viscous yet uniform and stable. Why it matters: Recognizing these properties helps in quality control, formulation stability testing, and determining whether a mixture truly qualifies as a solution in scientific and industrial contexts.

A liquid solution is a homogeneous mixture in which a liquid acts as the solvent, and one or more substances solid, liquid, or gas are dissolved in it as solutes. In simpler terms, it’s a uniform blend where the components are mixed at a molecular level and cannot be separated by simple filtration. The key feature is that the composition is the same throughout, meaning every drop of the solution contains the same ratio of solvent to solute. Example: The most familiar liquid solution is saltwater—water (the solvent) mixed with salt (the solute). When the salt dissolves, its ions disperse evenly in the water, creating a uniform taste and composition throughout. Other examples include sugar syrup (water + sugar), vinegar (water + acetic acid), and alcoholic beverages like wine (water + ethanol + various flavor compounds). From a scientific perspective, the solute particles in a liquid solution are typically smaller than 1 nanometer. This small size allows them to remain evenly distributed without settling over time. This property distinguishes solutions from suspensions and colloids, where particle size and stability differ. Why It Matters: Liquid solutions are fundamental in industries like pharmaceuticals (oral syrups), food and beverages (soft drinks, sauces), and chemical manufacturing (cleaning agents, inks). Understanding how solutes dissolve in solvents helps in controlling taste, stability, potency, and appearance.

A liquid solution is a homogeneous mixture in which a liquid acts as the solvent, and one or more substances solid, liquid, or gas are dissolved in it as solutes. In simpler terms, it’s a uniform blend where the components are mixed at a molecular level and cannot be separated by simple filtration. The key feature is that the composition is the same throughout, meaning every drop of the solution contains the same ratio of solvent to solute. Example: The most familiar liquid solution is saltwater—water (the solvent) mixed with salt (the solute). When the salt dissolves, its ions disperse evenly in the water, creating a uniform taste and composition throughout. Other examples include sugar syrup (water + sugar), vinegar (water + acetic acid), and alcoholic beverages like wine (water + ethanol + various flavor compounds). From a scientific perspective, the solute particles in a liquid solution are typically smaller than 1 nanometer. This small size allows them to remain evenly distributed without settling over time. This property distinguishes solutions from suspensions and colloids, where particle size and stability differ. Why It Matters: Liquid solutions are fundamental in industries like pharmaceuticals (oral syrups), food and beverages (soft drinks, sauces), and chemical manufacturing (cleaning agents, inks). Understanding how solutes dissolve in solvents helps in controlling taste, stability, potency, and appearance.

A solid–liquid solution is a homogeneous mixture in which a solid solute is completely dissolved in a liquid solvent, forming a single-phase system with uniform composition throughout. This is one of the most common types of solutions encountered in daily life, laboratories, and industries. The solid particles are broken down at the molecular or ionic level and become evenly distributed among the liquid’s molecules, making them invisible to the naked eye. Key examples include: Salt in water – Sodium chloride dissolves in water to produce a saline solution. This is used in cooking, preservation, and medical applications (e.g., IV saline drips). Sugar in water – Used in beverages, syrups, and confectionery manufacturing. Sugar molecules interact with water molecules via hydrogen bonding, leading to complete dissolution. Copper sulfate in water – Forms a bright blue solution widely used in laboratories, agriculture (as a fungicide), and electroplating. Potassium permanganate in water – Produces a purple-colored solution, used as an oxidizing agent in chemical reactions and water treatment. Vitamin C powder in water – A pharmaceutical preparation for quick absorption in the body. Important characteristics: The mixture remains stable with no sedimentation. The solute cannot be separated by ordinary filtration. Particle size is less than 1 nanometer, preventing light scattering. Applications: Medical field – Oral rehydration salts (ORS) are solid–liquid solutions that restore electrolytes in patients. Food industry – Brines and sugar syrups are vital for preservation and flavoring. Industrial processes – Solutions of solid chemicals in water are used in cleaning, plating, and manufacturing. Understanding solid–liquid solutions is essential for controlling solubility, temperature effects, and concentration factors that directly influence product quality and effectiveness.

A solid–liquid solution is a homogeneous mixture in which a solid solute is completely dissolved in a liquid solvent, forming a single-phase system with uniform composition throughout. This is one of the most common types of solutions encountered in daily life, laboratories, and industries. The solid particles are broken down at the molecular or ionic level and become evenly distributed among the liquid’s molecules, making them invisible to the naked eye. Key examples include: Salt in water – Sodium chloride dissolves in water to produce a saline solution. This is used in cooking, preservation, and medical applications (e.g., IV saline drips). Sugar in water – Used in beverages, syrups, and confectionery manufacturing. Sugar molecules interact with water molecules via hydrogen bonding, leading to complete dissolution. Copper sulfate in water – Forms a bright blue solution widely used in laboratories, agriculture (as a fungicide), and electroplating. Potassium permanganate in water – Produces a purple-colored solution, used as an oxidizing agent in chemical reactions and water treatment. Vitamin C powder in water – A pharmaceutical preparation for quick absorption in the body. Important characteristics: The mixture remains stable with no sedimentation. The solute cannot be separated by ordinary filtration. Particle size is less than 1 nanometer, preventing light scattering. Applications: Medical field – Oral rehydration salts (ORS) are solid–liquid solutions that restore electrolytes in patients. Food industry – Brines and sugar syrups are vital for preservation and flavoring. Industrial processes – Solutions of solid chemicals in water are used in cleaning, plating, and manufacturing. Understanding solid–liquid solutions is essential for controlling solubility, temperature effects, and concentration factors that directly influence product quality and effectiveness.

A liquid solution appears as a single, uniform phase with no visible separation of components, sedimentation, or cloudiness (unless the solution is naturally colored or slightly opaque due to dissolved substances). Because the solute is distributed at the molecular or ionic level, the mixture has the same appearance and composition throughout whether you sample it from the top, middle, or bottom. Visual characteristics of a liquid solution: Uniformity – The entire mixture looks consistent to the naked eye; there are no particles, droplets, or layers visible. Transparency – Most liquid solutions are clear (like saltwater or sugar water), although they can also be colored if the solute or solvent has color (e.g., copper sulfate in water gives a blue solution). No settling – Unlike suspensions, liquid solutions remain stable over time without the solute settling at the bottom. No light scattering – A true solution does not scatter light (no Tyndall effect), which helps distinguish it from colloids. Examples: Clear saltwater – transparent, colorless, uniform appearance. Iodine in alcohol (tincture of iodine) – uniform brown liquid. Ethanol in water – completely clear and colorless. How to recognize in practice: If you shine light through the liquid and it passes without scattering, it’s likely a true solution. If the mixture remains unchanged after standing still for hours or days, it’s likely a solution rather than a suspension. If you cannot filter out the solute using normal filter paper, it’s a true solution. In industrial and laboratory contexts, recognizing a liquid solution is important for quality control. For example, in pharmaceuticals, the clarity of an oral solution indicates proper dissolution of the active ingredient, while in beverages, uniformity ensures consistent taste and composition.

A liquid solution appears as a single, uniform phase with no visible separation of components, sedimentation, or cloudiness (unless the solution is naturally colored or slightly opaque due to dissolved substances). Because the solute is distributed at the molecular or ionic level, the mixture has the same appearance and composition throughout whether you sample it from the top, middle, or bottom. Visual characteristics of a liquid solution: Uniformity – The entire mixture looks consistent to the naked eye; there are no particles, droplets, or layers visible. Transparency – Most liquid solutions are clear (like saltwater or sugar water), although they can also be colored if the solute or solvent has color (e.g., copper sulfate in water gives a blue solution). No settling – Unlike suspensions, liquid solutions remain stable over time without the solute settling at the bottom. No light scattering – A true solution does not scatter light (no Tyndall effect), which helps distinguish it from colloids. Examples: Clear saltwater – transparent, colorless, uniform appearance. Iodine in alcohol (tincture of iodine) – uniform brown liquid. Ethanol in water – completely clear and colorless. How to recognize in practice: If you shine light through the liquid and it passes without scattering, it’s likely a true solution. If the mixture remains unchanged after standing still for hours or days, it’s likely a solution rather than a suspension. If you cannot filter out the solute using normal filter paper, it’s a true solution. In industrial and laboratory contexts, recognizing a liquid solution is important for quality control. For example, in pharmaceuticals, the clarity of an oral solution indicates proper dissolution of the active ingredient, while in beverages, uniformity ensures consistent taste and composition.

Before diving into the study of liquid solutions, it’s essential to have a strong grasp of fundamental chemistry topics that lay the groundwork for understanding solution behavior, interactions, and properties. These prerequisite chapters ensure you can connect theory with real-world applications and avoid confusion when dealing with advanced concepts like colligative properties, solubility curves, and Raoult’s Law. Key chapters to master beforehand include: Basic Concepts of Chemistry Understanding matter, types of mixtures (homogeneous vs. heterogeneous), and phases of matter. Familiarity with terms like solute, solvent, concentration, and phase. Structure of Matter and States of Matter Particle nature of matter and kinetic theory of gases and liquids. How intermolecular forces (hydrogen bonding, van der Waals, dipole–dipole) affect miscibility and solubility. Mole Concept and Stoichiometry Ability to calculate moles, molarity, molality, mass percent, and mole fraction. This is critical for expressing and comparing solution concentrations. Thermodynamics Concepts like enthalpy, entropy, and Gibbs free energy to understand why substances dissolve or resist dissolving. Heat changes during mixing (endothermic vs. exothermic). Chemical Bonding Nature of ionic, covalent, and hydrogen bonds. How polarity of molecules affects solubility (“like dissolves like” principle). Physical Properties of Liquids Surface tension, viscosity, and vapor pressure, which are directly related to solution behavior. Laws of Chemical Combination & Gas Laws (for gas–liquid solutions) Ideal gas law and partial pressures, important when studying gases dissolved in liquids (e.g., carbonated drinks). Why these are important : Studying these chapters first allows you to visualize molecular interactions, calculate concentrations confidently, and understand deviations from ideal behavior. For example, without knowing the mole concept, it would be difficult to apply Raoult’s Law. Without an understanding of intermolecular forces, predicting miscibility between liquids would be guesswork.By building this foundation, you’ll be able to approach liquid solution chemistry not as isolated facts but as interconnected principles that apply to real-world systems—whether in pharmaceuticals, environmental science, or industrial processes.

Before diving into the study of liquid solutions, it’s essential to have a strong grasp of fundamental chemistry topics that lay the groundwork for understanding solution behavior, interactions, and properties. These prerequisite chapters ensure you can connect theory with real-world applications and avoid confusion when dealing with advanced concepts like colligative properties, solubility curves, and Raoult’s Law. Key chapters to master beforehand include: Basic Concepts of Chemistry Understanding matter, types of mixtures (homogeneous vs. heterogeneous), and phases of matter. Familiarity with terms like solute, solvent, concentration, and phase. Structure of Matter and States of Matter Particle nature of matter and kinetic theory of gases and liquids. How intermolecular forces (hydrogen bonding, van der Waals, dipole–dipole) affect miscibility and solubility. Mole Concept and Stoichiometry Ability to calculate moles, molarity, molality, mass percent, and mole fraction. This is critical for expressing and comparing solution concentrations. Thermodynamics Concepts like enthalpy, entropy, and Gibbs free energy to understand why substances dissolve or resist dissolving. Heat changes during mixing (endothermic vs. exothermic). Chemical Bonding Nature of ionic, covalent, and hydrogen bonds. How polarity of molecules affects solubility (“like dissolves like” principle). Physical Properties of Liquids Surface tension, viscosity, and vapor pressure, which are directly related to solution behavior. Laws of Chemical Combination & Gas Laws (for gas–liquid solutions) Ideal gas law and partial pressures, important when studying gases dissolved in liquids (e.g., carbonated drinks). Why these are important : Studying these chapters first allows you to visualize molecular interactions, calculate concentrations confidently, and understand deviations from ideal behavior. For example, without knowing the mole concept, it would be difficult to apply Raoult’s Law. Without an understanding of intermolecular forces, predicting miscibility between liquids would be guesswork.By building this foundation, you’ll be able to approach liquid solution chemistry not as isolated facts but as interconnected principles that apply to real-world systems—whether in pharmaceuticals, environmental science, or industrial processes.

A liquid in liquid solution refers to a homogeneous mixture where both the solute and the solvent are liquids, and the solute is completely miscible or soluble in the solvent at the molecular level. In this arrangement, one liquid (the solvent) serves as the continuous phase, while the other liquid (the solute) is dispersed so uniformly that the mixture appears as a single phase with no visible separation.For a liquid–liquid solution to form, the two liquids must have compatible intermolecular forces. Polar liquids (like water, ethanol, glycerin) tend to mix readily with other polar liquids due to hydrogen bonding or dipole–dipole interactions. Non-polar liquids (like benzene, toluene, hexane) generally mix well with other non-polar liquids due to van der Waals forces. However, polar and non-polar liquids usually do not mix unless a third agent, such as an emulsifier or surfactant, is introduced. Key examples include: Ethanol in water – Used in beverages, disinfectants, and pharmaceutical tinctures. Acetic acid in water – Forms vinegar, a staple in culinary and preservation processes. Perfume bases – Essential oils dissolved in ethanol for fragrance products. Applications of liquid–liquid solutions are extensive: In pharmaceuticals, they are used for oral solutions, topical applications, and drug delivery systems. In food and beverage, they help create stable flavor blends and syrups. In industrial chemistry, they are used in solvent extraction, liquid–liquid chromatography, and fuel formulation.

A liquid in liquid solution refers to a homogeneous mixture where both the solute and the solvent are liquids, and the solute is completely miscible or soluble in the solvent at the molecular level. In this arrangement, one liquid (the solvent) serves as the continuous phase, while the other liquid (the solute) is dispersed so uniformly that the mixture appears as a single phase with no visible separation.For a liquid–liquid solution to form, the two liquids must have compatible intermolecular forces. Polar liquids (like water, ethanol, glycerin) tend to mix readily with other polar liquids due to hydrogen bonding or dipole–dipole interactions. Non-polar liquids (like benzene, toluene, hexane) generally mix well with other non-polar liquids due to van der Waals forces. However, polar and non-polar liquids usually do not mix unless a third agent, such as an emulsifier or surfactant, is introduced. Key examples include: Ethanol in water – Used in beverages, disinfectants, and pharmaceutical tinctures. Acetic acid in water – Forms vinegar, a staple in culinary and preservation processes. Perfume bases – Essential oils dissolved in ethanol for fragrance products. Applications of liquid–liquid solutions are extensive: In pharmaceuticals, they are used for oral solutions, topical applications, and drug delivery systems. In food and beverage, they help create stable flavor blends and syrups. In industrial chemistry, they are used in solvent extraction, liquid–liquid chromatography, and fuel formulation.

A liquid–liquid solution is a homogeneous mixture in which both the solute and the solvent are in the liquid state. In these solutions, one liquid is dispersed at the molecular level within another, forming a single-phase system that appears uniform throughout. For a liquid–liquid solution to form, the two liquids must be miscible meaning they can mix in all proportions without separating into layers under normal conditions. Key examples include : Alcohol in water – Ethanol (liquid) dissolves completely in water to produce alcoholic beverages such as wine or spirits. This is one of the most common liquid–liquid solutions in daily life. Acetic acid in water – Found in vinegar, acetic acid blends uniformly with water, creating a sharp-tasting culinary solution. Glycerin in water – Used in pharmaceutical syrups, cosmetics, and moisturizers, glycerin dissolves easily in water to form a smooth-textured solution. Essential oils in alcohol – Used in perfumes and aromatherapy, essential oils dissolve in ethanol to produce aromatic liquid–liquid solutions. Liquid fuel blends – Gasoline is often a mixture of different liquid hydrocarbons that remain completely miscible with one another. Important points about liquid–liquid solutions : They often involve polar + polar combinations (e.g., ethanol and water) or non-polar + non-polar combinations (e.g., benzene and toluene). Polar and non-polar liquids generally do not form solutions due to differences in intermolecular forces (e.g., oil and water are immiscible unless an emulsifier is used). They are widely used in chemical extraction, medicinal formulations, flavors and fragrances, and industrial lubricants.

A liquid–liquid solution is a homogeneous mixture in which both the solute and the solvent are in the liquid state. In these solutions, one liquid is dispersed at the molecular level within another, forming a single-phase system that appears uniform throughout. For a liquid–liquid solution to form, the two liquids must be miscible meaning they can mix in all proportions without separating into layers under normal conditions. Key examples include : Alcohol in water – Ethanol (liquid) dissolves completely in water to produce alcoholic beverages such as wine or spirits. This is one of the most common liquid–liquid solutions in daily life. Acetic acid in water – Found in vinegar, acetic acid blends uniformly with water, creating a sharp-tasting culinary solution. Glycerin in water – Used in pharmaceutical syrups, cosmetics, and moisturizers, glycerin dissolves easily in water to form a smooth-textured solution. Essential oils in alcohol – Used in perfumes and aromatherapy, essential oils dissolve in ethanol to produce aromatic liquid–liquid solutions. Liquid fuel blends – Gasoline is often a mixture of different liquid hydrocarbons that remain completely miscible with one another. Important points about liquid–liquid solutions : They often involve polar + polar combinations (e.g., ethanol and water) or non-polar + non-polar combinations (e.g., benzene and toluene). Polar and non-polar liquids generally do not form solutions due to differences in intermolecular forces (e.g., oil and water are immiscible unless an emulsifier is used). They are widely used in chemical extraction, medicinal formulations, flavors and fragrances, and industrial lubricants.

A liquid solution is a homogeneous mixture in which a liquid solvent dissolves one or more solutes which can be solid, liquid, or gas—to form a single-phase system that appears uniform throughout. In this type of mixture, the solute particles are dispersed at the molecular or ionic level within the solvent, making them invisible to the naked eye and impossible to separate by simple filtration.In a liquid solution, the solvent determines the phase of the solution (in this case, liquid), while the solute determines the chemical and physical properties to some extent. The solvent molecules surround and interact with solute particles through intermolecular forces such as hydrogen bonding, dipole–dipole interactions, or van der Waals forces. This stable arrangement prevents the solute from settling out over time. Common examples include : Saltwater – sodium chloride (solid) dissolved in water (liquid). Alcoholic beverages – ethanol (liquid) dissolved in water (liquid). Carbonated drinks – carbon dioxide gas dissolved in flavored liquid. Key characteristics of a liquid solution: Uniform composition throughout the mixture. Particle size generally less than 1 nanometer. No light scattering (unlike colloids, which exhibit the Tyndall effect). Stable under normal conditions without sedimentation. Applications span almost every industry—chemistry, pharmaceuticals, food and beverage, cosmetics, and environmental science. For instance, in medicine, oral syrups are liquid solutions that ensure fast absorption. In chemical engineering, liquid solutions serve as reaction media for synthesizing materials.Understanding liquid solutions is foundational to predicting solubility, reaction rates, and separation processes, making it a critical topic in both academic study and real-world applications.

A liquid solution is a homogeneous mixture in which a liquid solvent dissolves one or more solutes which can be solid, liquid, or gas—to form a single-phase system that appears uniform throughout. In this type of mixture, the solute particles are dispersed at the molecular or ionic level within the solvent, making them invisible to the naked eye and impossible to separate by simple filtration.In a liquid solution, the solvent determines the phase of the solution (in this case, liquid), while the solute determines the chemical and physical properties to some extent. The solvent molecules surround and interact with solute particles through intermolecular forces such as hydrogen bonding, dipole–dipole interactions, or van der Waals forces. This stable arrangement prevents the solute from settling out over time. Common examples include : Saltwater – sodium chloride (solid) dissolved in water (liquid). Alcoholic beverages – ethanol (liquid) dissolved in water (liquid). Carbonated drinks – carbon dioxide gas dissolved in flavored liquid. Key characteristics of a liquid solution: Uniform composition throughout the mixture. Particle size generally less than 1 nanometer. No light scattering (unlike colloids, which exhibit the Tyndall effect). Stable under normal conditions without sedimentation. Applications span almost every industry—chemistry, pharmaceuticals, food and beverage, cosmetics, and environmental science. For instance, in medicine, oral syrups are liquid solutions that ensure fast absorption. In chemical engineering, liquid solutions serve as reaction media for synthesizing materials.Understanding liquid solutions is foundational to predicting solubility, reaction rates, and separation processes, making it a critical topic in both academic study and real-world applications.

A monophasic liquid dosage form is a pharmaceutical preparation in which the active drug ingredient(s) are uniformly dissolved or dispersed in a single-phase liquid medium, resulting in a clear or homogeneously opaque solution. The term monophasic means that there is only one continuous phase—no visible separation of layers or sedimentation should occur under normal storage conditions.These dosage forms are designed for ease of administration, accurate dosing, and rapid absorption. They can be intended for oral, topical, ophthalmic, otic, nasal, or parenteral use, depending on the formulation and therapeutic goal. Because the active ingredient is molecularly dispersed in the vehicle, monophasic liquids generally provide consistent potency throughout the container and allow for immediate drug availability upon administration. Examples include : Oral solutions – e.g., paracetamol solution for fever relief. Syrups – sucrose-based solutions containing drug and flavoring agents, such as cough syrups. Elixirs – sweetened hydro-alcoholic solutions used for water-insoluble drugs. Tinctures – alcoholic extracts of plant or animal materials. Ophthalmic solutions – sterile eye drops for conditions like glaucoma or dryness. Key advantages : Easy swallowing for children, elderly, or patients with dysphagia. Faster onset of action compared to solid dosage forms, as the drug does not require dissolution in the body. Flexibility in dose adjustment by altering the volume administered. Formulation considerations include solubility of the drug, chemical stability in solution, microbial preservation, and patient acceptability in terms of taste, viscosity, and appearance. Preservatives (e.g., parabens), stabilizers (e.g., antioxidants), and flavoring agents are often added to improve shelf life and palatability.In pharmaceutical practice, the concept of monophasic liquid dosage forms is fundamental because it directly affects bioavailability, patient compliance, and therapeutic success.

A monophasic liquid dosage form is a pharmaceutical preparation in which the active drug ingredient(s) are uniformly dissolved or dispersed in a single-phase liquid medium, resulting in a clear or homogeneously opaque solution. The term monophasic means that there is only one continuous phase—no visible separation of layers or sedimentation should occur under normal storage conditions.These dosage forms are designed for ease of administration, accurate dosing, and rapid absorption. They can be intended for oral, topical, ophthalmic, otic, nasal, or parenteral use, depending on the formulation and therapeutic goal. Because the active ingredient is molecularly dispersed in the vehicle, monophasic liquids generally provide consistent potency throughout the container and allow for immediate drug availability upon administration. Examples include : Oral solutions – e.g., paracetamol solution for fever relief. Syrups – sucrose-based solutions containing drug and flavoring agents, such as cough syrups. Elixirs – sweetened hydro-alcoholic solutions used for water-insoluble drugs. Tinctures – alcoholic extracts of plant or animal materials. Ophthalmic solutions – sterile eye drops for conditions like glaucoma or dryness. Key advantages : Easy swallowing for children, elderly, or patients with dysphagia. Faster onset of action compared to solid dosage forms, as the drug does not require dissolution in the body. Flexibility in dose adjustment by altering the volume administered. Formulation considerations include solubility of the drug, chemical stability in solution, microbial preservation, and patient acceptability in terms of taste, viscosity, and appearance. Preservatives (e.g., parabens), stabilizers (e.g., antioxidants), and flavoring agents are often added to improve shelf life and palatability.In pharmaceutical practice, the concept of monophasic liquid dosage forms is fundamental because it directly affects bioavailability, patient compliance, and therapeutic success.

An ideal solution is a liquid mixture in which the intermolecular forces between solute–solute, solvent–solvent, and solute–solvent molecules are identical in strength and nature. Because the interactions are the same, mixing the components does not cause any change in properties like enthalpy or volume. According to Raoult’s Law, the partial vapor pressure of each component in an ideal solution is directly proportional to its mole fraction in the mixture. Examples include benzene and toluene or hexane and heptane—systems where molecular size, shape, and polarity are very similar. In an ideal solution: Enthalpy of mixing (ΔHmix) = 0 (no heat is absorbed or released) Volume change on mixing (ΔVmix) = 0 The solution perfectly obeys Raoult’s Law across all concentrations. A non-ideal solution, on the other hand, deviates from Raoult’s Law because the forces of attraction between unlike molecules are either stronger or weaker than those between like molecules. This leads to positive or negative deviations: Positive deviation (e.g., ethanol + water at high ethanol content) occurs when solute–solvent interactions are weaker than those in the pure components, leading to higher vapor pressure and endothermic mixing (ΔHmix > 0). Negative deviation (e.g., acetone + chloroform) occurs when solute–solvent interactions are stronger than in pure substances, leading to lower vapor pressure and exothermic mixing (ΔHmix < 0). Forces of interaction in liquids include hydrogen bonding, van der Waals forces, and dipole–dipole interactions. In ideal solutions, these forces are balanced across all molecular pairs. In non-ideal solutions, the imbalance alters properties such as boiling point, freezing point, and vapor pressure. Real-world relevance : Pharmaceuticals require understanding non-ideal behavior to predict drug solubility and stability. Industrial separations like distillation depend on deviations from ideality to design efficient processes. Environmental chemistry uses these principles to predict pollutant behavior in water or organic phases.

An ideal solution is a liquid mixture in which the intermolecular forces between solute–solute, solvent–solvent, and solute–solvent molecules are identical in strength and nature. Because the interactions are the same, mixing the components does not cause any change in properties like enthalpy or volume. According to Raoult’s Law, the partial vapor pressure of each component in an ideal solution is directly proportional to its mole fraction in the mixture. Examples include benzene and toluene or hexane and heptane—systems where molecular size, shape, and polarity are very similar. In an ideal solution: Enthalpy of mixing (ΔHmix) = 0 (no heat is absorbed or released) Volume change on mixing (ΔVmix) = 0 The solution perfectly obeys Raoult’s Law across all concentrations. A non-ideal solution, on the other hand, deviates from Raoult’s Law because the forces of attraction between unlike molecules are either stronger or weaker than those between like molecules. This leads to positive or negative deviations: Positive deviation (e.g., ethanol + water at high ethanol content) occurs when solute–solvent interactions are weaker than those in the pure components, leading to higher vapor pressure and endothermic mixing (ΔHmix > 0). Negative deviation (e.g., acetone + chloroform) occurs when solute–solvent interactions are stronger than in pure substances, leading to lower vapor pressure and exothermic mixing (ΔHmix < 0). Forces of interaction in liquids include hydrogen bonding, van der Waals forces, and dipole–dipole interactions. In ideal solutions, these forces are balanced across all molecular pairs. In non-ideal solutions, the imbalance alters properties such as boiling point, freezing point, and vapor pressure. Real-world relevance : Pharmaceuticals require understanding non-ideal behavior to predict drug solubility and stability. Industrial separations like distillation depend on deviations from ideality to design efficient processes. Environmental chemistry uses these principles to predict pollutant behavior in water or organic phases.

A liquid solution is a broad term for any homogeneous mixture where the solvent is in the liquid state. This solvent can be water, oil, alcohol, or any other liquid capable of dissolving a solute. In a liquid solution, the solute can be a solid, liquid, or gas, and the defining feature is that the resulting mixture is uniform and exists entirely in the liquid phase. Examples include: Saltwater (solid salt dissolved in water) Gasoline blend (various hydrocarbons mixed together) Carbonated beverages (carbon dioxide gas dissolved in liquid) An aqueous solution is a specific type of liquid solution in which water is the solvent. The term aqueous comes from the Latin aqua , meaning water. This means all aqueous solutions are liquid solutions, but not all liquid solutions are aqueous. Examples include: Sugar in water (used in syrups and beverages) Vinegar (acetic acid dissolved in water) Saline solution (sodium chloride in water, often used medically) Key differences: Solvent type – Liquid solutions can have any liquid as the solvent, while aqueous solutions must have water as the solvent. Chemical behavior – Water-based solutions often participate in acid-base reactions, hydrolysis, and other aqueous chemistry phenomena, which may not occur in non-water liquid solutions. Applications – Aqueous solutions dominate in biological, pharmaceutical, and environmental contexts because water is the universal biological solvent. Non-aqueous liquid solutions are common in paints, fuels, and lubricants.

A liquid solution is a broad term for any homogeneous mixture where the solvent is in the liquid state. This solvent can be water, oil, alcohol, or any other liquid capable of dissolving a solute. In a liquid solution, the solute can be a solid, liquid, or gas, and the defining feature is that the resulting mixture is uniform and exists entirely in the liquid phase. Examples include: Saltwater (solid salt dissolved in water) Gasoline blend (various hydrocarbons mixed together) Carbonated beverages (carbon dioxide gas dissolved in liquid) An aqueous solution is a specific type of liquid solution in which water is the solvent. The term aqueous comes from the Latin aqua , meaning water. This means all aqueous solutions are liquid solutions, but not all liquid solutions are aqueous. Examples include: Sugar in water (used in syrups and beverages) Vinegar (acetic acid dissolved in water) Saline solution (sodium chloride in water, often used medically) Key differences: Solvent type – Liquid solutions can have any liquid as the solvent, while aqueous solutions must have water as the solvent. Chemical behavior – Water-based solutions often participate in acid-base reactions, hydrolysis, and other aqueous chemistry phenomena, which may not occur in non-water liquid solutions. Applications – Aqueous solutions dominate in biological, pharmaceutical, and environmental contexts because water is the universal biological solvent. Non-aqueous liquid solutions are common in paints, fuels, and lubricants.

A solid solution and a liquid solution are both homogeneous mixtures, but they differ in their phase, composition, and practical applications.A solid solution is a uniform mixture in the solid state, where atoms, ions, or molecules of a solute are incorporated into the crystal lattice of a solid solvent without disrupting its structure. The solute may be present in small or significant amounts, but it is dispersed at the atomic or molecular level. For example, alloys such as brass (zinc dissolved in copper) and stainless steel (carbon and other elements dissolved in iron) are solid solutions. These are generally formed by melting the components together and then cooling them so the solute becomes embedded in the crystal structure of the solvent.A liquid solution, on the other hand, is a homogeneous mixture in the liquid state, where the solute is dissolved in a liquid solvent. Common examples include saltwater (solid sodium chloride dissolved in water) and alcoholic beverages (ethanol dissolved in water). In liquid solutions, the solute particles are dispersed at the molecular level and can be solids, liquids, or gases.The key differences can be summarized as follows: State : Solid vs. liquid Formation : Solid solutions often require melting and solidification; liquid solutions are typically formed by stirring, shaking, or heating. Mobility of particles : In solids, atoms are fixed within a lattice; in liquids, molecules can move freely. Applications : Solid solutions are crucial in metallurgy, electronics, and construction; liquid solutions are essential in chemistry, medicine, and food industries. Understanding this difference is important for material selection, product formulation, and predicting how mixtures will behave under various conditions.

A solid solution and a liquid solution are both homogeneous mixtures, but they differ in their phase, composition, and practical applications.A solid solution is a uniform mixture in the solid state, where atoms, ions, or molecules of a solute are incorporated into the crystal lattice of a solid solvent without disrupting its structure. The solute may be present in small or significant amounts, but it is dispersed at the atomic or molecular level. For example, alloys such as brass (zinc dissolved in copper) and stainless steel (carbon and other elements dissolved in iron) are solid solutions. These are generally formed by melting the components together and then cooling them so the solute becomes embedded in the crystal structure of the solvent.A liquid solution, on the other hand, is a homogeneous mixture in the liquid state, where the solute is dissolved in a liquid solvent. Common examples include saltwater (solid sodium chloride dissolved in water) and alcoholic beverages (ethanol dissolved in water). In liquid solutions, the solute particles are dispersed at the molecular level and can be solids, liquids, or gases.The key differences can be summarized as follows: State : Solid vs. liquid Formation : Solid solutions often require melting and solidification; liquid solutions are typically formed by stirring, shaking, or heating. Mobility of particles : In solids, atoms are fixed within a lattice; in liquids, molecules can move freely. Applications : Solid solutions are crucial in metallurgy, electronics, and construction; liquid solutions are essential in chemistry, medicine, and food industries. Understanding this difference is important for material selection, product formulation, and predicting how mixtures will behave under various conditions.

Liquid Solutions Class 12 Chemistry Notes – Concepts, Types, and Colligative Properties

INTRODUCTION

A homogeneous mixture of two or more components in which the phase of at least one component belongs to the phase of solution, that component is known as solvent and others as solute. The size of solute particle differentiate solution [0.2 – 2.0 nm] from its contemporary colloids [2.0–1000 nm] and suspension in which particle diameter is greater than 1000 nm and they are unstable and particle settle down due to gravitational pull.

Types of solution

There are nine possible combinations of the three phases of solid, liquid and gas. Some important combinations are given below:

Sr. No.	Combination	Example
(i)	Gas in gas	Air (O₂ + N₂ + Ar + CO₂)
(ii)	Gas in liquid	Cold drinks (carbonated water)
(iii)	Gas in solid	H₂ in palladium metal
(iv)	Liquid in liquid	Gasoline mixture, wine
(v)	Liquid in solid	Dental amalgam (mercury in silver), H₂O in CuSO₄ crystal
(vi)	Solid in liquid	Sugar syrup
(vii)	Solid in solid	Brass, 14–carat gold

Essentials to Identify or Rank Solvent in a Solution:

Phase Rule:
The phase of the solution is the same as the phase of the solvent.
- Example: For gas or solid dissolved in a liquid, the solvent is liquid.
Major Component Rule (for liquid–liquid solutions):
In binary or ternary liquid solutions, the component with the largest proportion is considered the solvent.
Special Rule for Aqueous Solutions:
If water is a component, it is generally called the solvent, even if it is in lesser proportion in some cases, due to its role as the universal solvent.
- Example: In ethyl alcohol + water solution, water is the solvent.

Concentration units and ways of expression

Mass percentage: Mass% = (wt. of solute / wt. of solution) × 100
Volume percentage: Vol% = (Vol. of solute / Vol. of solution) × 100
Molality (m): m = moles of solute / weight of solvent (in kg)
Molarity (M): M = moles of solute / litres of solution
Normality (N): N = no. of gram equivalents of solute / litres of solution
Mole fraction: X_solute = n / (n + N) ; X_solvent = N / (n + N)

Example-1 : A student finds that 31.26 ml of a 0.165 M solution of barium hydroxide, Ba(OH)₂, solution is required to just neutralize 25.00 ml of a citric acid, H₃C₆H₅O₇, solution. What is the concentration of the H₃C₆H₅O₇ solution?

(A) 0.413 M

(B) 0.309 M

(D) 0.138 M

Solution. (D).
Citric acid is tricarboxylic acid, so ‘n’ factor is 3
Ba(OH)₂ vs citric acid
2 × M₁V₁ = 3 × M₂V₂
M₂ = (2/3) × (M₁V₁ / V₂)
= (2/3) × (0.165 × 31.26 / 25)
= 0.138 M

Example 2: What is the density (in g ml^–1) of a 3.60 M aqueous sulfuric acid solution that is 29.0% H₂SO₄ by mass?
(A) 1.22

(B) 1.45

(D) 1.88

Solution. (A).

Density = (3.6 × 98) / (10 × 29) = 1.22

Molarity = (10 × density × percentage) / Molecular weight

Vapour pressure of solution

The tendency of vaporisation is some what in lesser extent in solution than pure solvent because the solvent–solvent molecule attraction force is less than the solvent–solute attraction force so escaping tendency of solvent molecule in solution from liquid phase to vapour phase becoming less than pure solvent.

Raoults law for volatile solutes

The vapour pressure of any component at given temperature is the product of mole fraction of the component in solution with vapour pressure of the component in pure state.

For a binary mixture of two volatile components A and B with mole fraction X_A and X_B with pure component pressure P_A⁰ and P_B⁰ respectively.

According to Raoult's law:

P_A = P_A⁰ × X_A

P_B = P_B⁰ × X_B

where, P_A and P_B are vapour pressures of A and B above the solution they form.
So total pressure P_T = P_A + P_B:

P_T = P_A⁰ × X_A + P_B⁰ × X_B

The solutions which are ideal obey Raoult's law for any composition of A and B.

The vapour pressure of solution containing non-volatile solute is less than pure solvent vapour pressure, why?

Explanation: The attraction between solute and solvent molecules is greater than the attraction force among solvent–solvent molecules so the escaping tendency from liquid phase to gaseous phase becomes less due to increased attraction by molecule.

The relation between mole fraction of solvent and vapour pressure was first pointed out by Francis Marie Raoult's "Vapour pressure of solution is proportional to the mole fraction of solvent".

P_A ∝ X_A

P_A = P_A⁰ × X_A[As for pure solvent X_A = 1, P_A = P_A⁰]

where,
• P_A = vapour pressure of solution,
• P_A⁰ = vapour pressure of pure solution,
• X_A = mole fraction of solvent

P_A = P_A⁰ [1 – X_B]

where, X_B is mole fraction of single non-volatile solute in solution.

P_A⁰ – P_A = P_A⁰ X_B
( P_A⁰ – P_A P_A⁰ ) = X_B
ΔP/P_A⁰ = relative lowering of vapour pressure and is equal to mole fraction of non-volatile solute

All above relation is valid only for ideal solutions (that practically never exist but assumed that solution having concentration < 0.2 M are ideal).
So, ideal solutions are those which obey Raoult’s law for all composition.

Determination of Molar Masses from Lowering of Vapour Pressure

It is possible to calculate molar masses of non-volatile non-electrolytic solutes by measuring vapour pressures of their dilute solutions.
Suppose, a given mass, w gram, of a solute of molar mass m, dissolved in W gram of solvent of molar mass M, lowers the vapour pressure from \( P_1^0 \) to \( P_1 \).
Then, by Equation

\[ \frac{P_1^0 - P_1}{P_1^0} = \frac{n}{N+n} = \frac{w/m}{W/M + w/m} \]
Since in dilute solutions, n is very small as compared to N, Hence
\[ \frac{P_1^0 - P_1}{P_1^0} = \frac{n}{N} = \frac{w/m}{W/M} = \frac{w M}{W m} \]
or,
\[ m = \frac{wM}{W(P_1^0 - P_1)/P_1^0} \]

Example 3: The vapour pressure of pure benzene at 25°C is 639.7 mm Hg and the vapour pressure of a solution of solute in benzene at 25°C is 631.9 mm Hg. The molality of the solution is

(A) 0.156
(B) 0.108
(C) 5.18
(D) 0.815

Solution: (A).

Molality = (^{P₀ - P_s}/_P₀) × 1000 / M

Putting the known values, ‘M’ = 0.156 moles/kg

Example 4: If P₀ & P_s be the vapour pressure of solvent and its solution respectively and N₁ and N₂ be the mole–fractions of solvent and solute respectively, then

(A) P_s = P₀ × N₂
(B) P₀ = P_s = P × N₂
(C) P_s = P₀ × N₁
(D) (^{P₀ - P_s}/_{P_s}) = N₁/(N₁ + N₂)

Solution: (C)

IDEAL SOLUTION

Ideal solution obeys Raoult’s law for binary mixture of component A and B present in mixture with mole fraction Xₐ and Xᵦ. If both components are volatile in nature then partial pressure of each component PA and PB should be less than Pₐ⁰ [Pure component vapour pressure of A] and Pᵦ⁰.

But,
PA = Pₐ⁰ × Xₐ
PB = Pᵦ⁰ × Xᵦ

So, PA + PB = Ptotal = Pₐ⁰Xₐ + Pᵦ⁰Xᵦ

If a graph is plotted between vapour pressure and composition for ideal solution PA, PB, Ptotal are represented by straight lines.

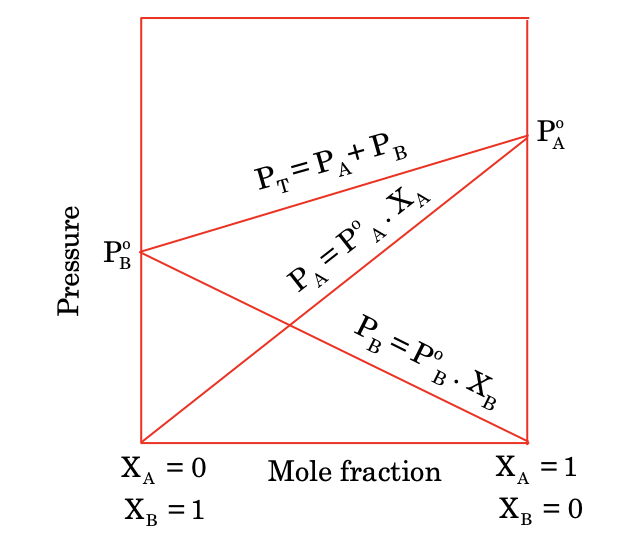
IDEAL SOLUTION

So, it can be stated in another way that ideal solution is that solution which obey Raoult’s law for any concentration.
This type of ideality is impossible in actual practice. This is why solutions with very dilute [< 0.2 M] assumed to behave ideally.
For ideal solution each component must have symmetry both in size and nature (molecular attraction with each other otherwise they do not behave ideally.

So for ideal solution,
ΔH_mix = 0, ΔV_mix = 0
P_total = P⁰_AX_A + P⁰_BX_B

Some examples of solution that is nearest to ideality.
(i) Benzene + Toluene
(ii) Hexane + Heptane
(iii) Ethyl bromide + Ethyl iodide
(iv) Chlorobenzene + Bromobenzene

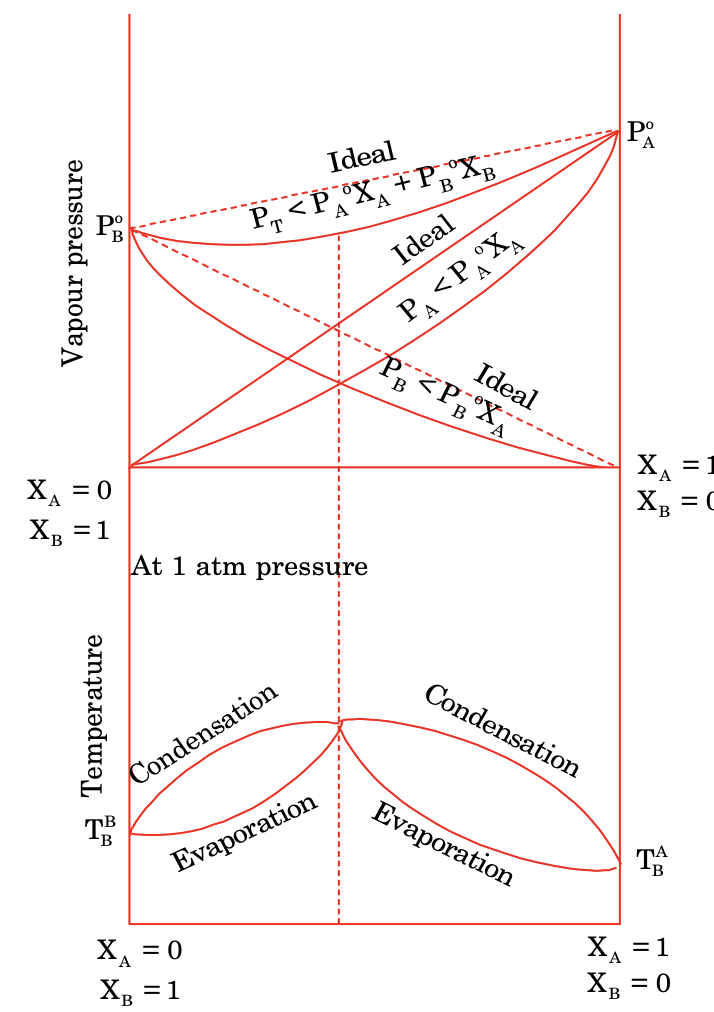
NON IDEAL SOLUTION

Due to dissymmetry in the size and nature of different components, they do not obey Raoult’s law. There are two type of non ideal solution of liquid components exists.

(a) Non ideal solution with positive deviation: They are characterised by
ΔH_mix = +ve (endothermic)
ΔV_mix = +ve (increase in volume)
P_total > P_A + P_B
P_total > P⁰_AX_A + P⁰_BX_B
P_A > P⁰_AX_A; P_B > P⁰_BX_B

This type of deviation occurs in components in which molar attraction is negligible with large size and shape difference.

They form minimum boiling azeotropic solution at a given composition.

Examples of non ideal solutions with positive deviation

(i) Acetone + Carbon disulphide

(ii) Acetone + Ethyl alcohol

(iii) Benzene + Acetone

(iv) Water + Methyl alcohol

(v) Ethyl alcohol + Water

(vi) Carbon tetrachloride + Chloroform

(vi) Carbon tetrachloride + Benzene

(vii) Carbon tetrachloride + Toluene

non ideal solutions

The boiling point of such composition mixture is lower than pure component boiling point of A and B respectively.
Azeotropic mixture can not be separated by simple distillation method because the composition of both vapour and liquid phase is same for both component and the boiling point remains constant till all the rest mixture evaporate so they can not be separated and they are also known as constant boiling mixture.

(b) Non–ideal solution with negative deviation
When the amount of molecular attraction between components A and B is valid and favoured by shape and size of them at proper composition. These are characterised by

ΔH_mix < 0
ΔV_mix < 0
P_A < P^o_AX_A ; P_B < P^o_BX_B
P_total < P^o_AX_A + P^o_BX_B

Such mixture form maximum boiling point azeotropic at definite composition.
Examples of non ideal solutions with negative deviation

Chloroform + Benzene
Chloroform + Acetone
Chloroform + Diethyl ether
Acetone + Aniline
HCl + H₂O
HNO₃ + H₂O
CH₃COOH + Pyridine

non-idal-solutions-liquid-solutions

Colligative Properties
The properties is depends upon the number of particles of solute in solution are called colligative properties. The following four colligative properties are:

(i) Relative Lowering of Vapour
The vapour pressure of solution containing non–volatile solute is less than pure solvent vapour pressure. This lowering of vapour pressure was formulated by Raoult’s law for
(a) Non volatile solute in solution
(b) For liquid component solution
The relation between mole fraction of solvent and vapour pressure is given by

⇒ (P_A^o - P_A) / P_A^o = X_B

⇒ ΔP / P_A^o = relative lowering of vapour pressure and is equal to mole fraction of non volatile solute

Example: One mole of non–volatile solute is dissolved in two moles of water. The vapour pressure of the solution relative to that of water is
(A) 2/3

(B) 1/3

(D) 3/2

Sol. (A).

P_A / P_A^o = X_A = 2 / (2+1) = 2 / 3

(ii) Depression in freezing point

The vapour pressure of a solution is always less than the pure solvent. Plotting the graph between vapour pressure and temperature for a phase diagram of solvent and solution. The curve obtained for solution lies below the curve of pure solvent and almost parallel.

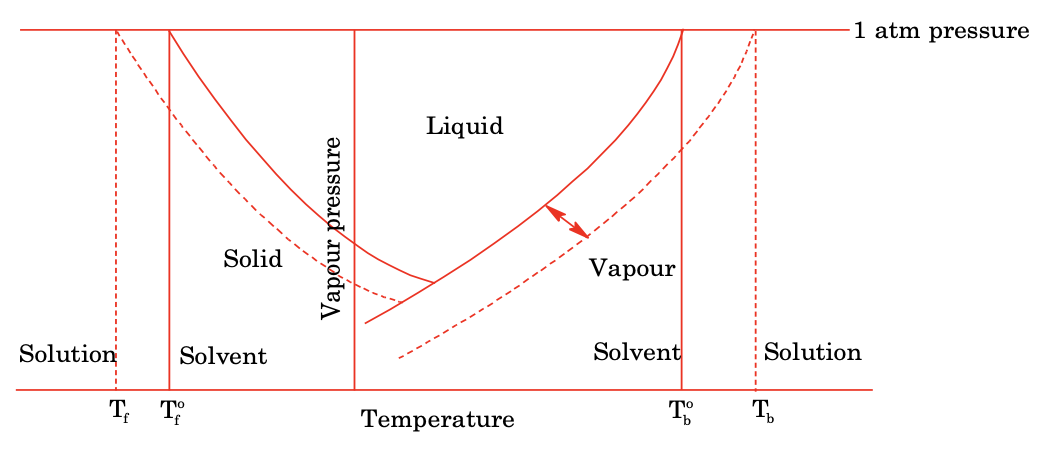
Depression in freezing point

For depression in freezing point

ΔT_f = T_f^° – T_f ∝ ΔP/P^° (Relative lowering of vapour pressure)
⇒ ΔT_f ∝ X_B
∝ W_B/M_B × 1000 / W_A/M_A × 1000 [X_B = W_B/M_B / ( W_A/M_A + W_B/M_B) (neglecting W_B/M_B in denominator)]
ΔT_f ∝ (W_B × 1000) / M_B / W_A/M_A × M_A/1000
ΔT_f = M_A · K_f / 1000 · m = K_f · m

where, K_f = molal depression constant
m = molality of solution
The unit for K_f = degree mol⁻¹ kg
The K_f is the property of solvent.

(iii) Elevation in boiling point
As seen from graph plotted in figure.
ΔT_b = T_b − T_b^° ∝ Relative lowering of vapour pressure
⇒ ΔT_b ∝ X_B
∝ W_B/W_A × M_A/(M_A + M_B) [W_B/M_B is neglected in denominator as it is small]
⇒ ΔT_b ∝ W_B/W_A × 1000/M_B × M_A/1000

⇒ ΔT_b = K · M_A / 1000 · m = K_b · m
where, K_b = molal elevation constant having unit degree kg mol⁻¹ and property of solvent only and m = molarity.
The value of K_f or K_b can be determined following the equation
K_f = 0.002 T_f² / L_f ; K_b = 0.002 T_b² / L_v
where, L_f and L_v are latent heat of freezing and vaporisation in cal/gm respectively and T_f = fusion temperature and T_b = boiling temperature at one atm pressure in Kelvin.

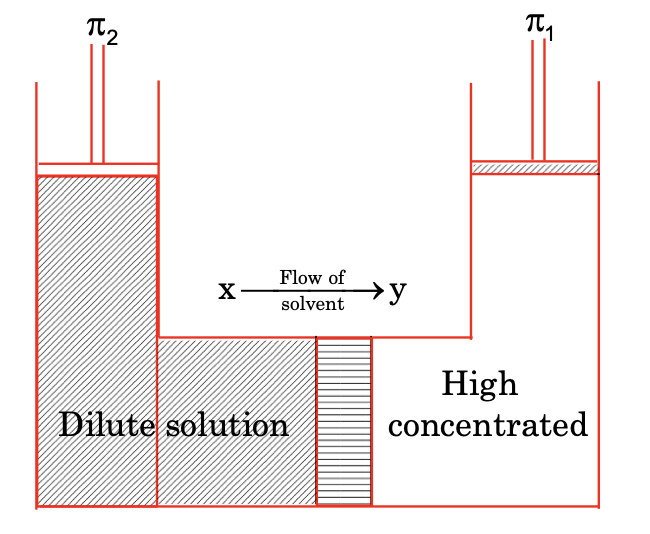
OSMOSIS

The flow of solvent from lower concentration solution towards high concentration separated by the semipermeable membrane (a membrane which only allows only liquid particles to pass through it) is known as osmosis.

Osmosis is also a colligative property of solution which depends on the concentration of solution and not on the nature of solute.

The phenomenona of osmosis play important part in all biological activity for the working of cell. For example: water rising up to leaf of long tall plant from soil, swelling of egg shell in fresh water shrinkage of egg in saline water etc. The preservation of pickle or fruit by keeping them in salt or sugar solution is also an application of osmosis. The water in bacterial cell comes out due to osmosis on high concentration salt and they perish.

(iv) Osmotic pressure
The pressure applied to stop the phenomenon of osmosis is known as osmotic pressure. It is indicated by π and has an analogous formula to ideal gas.
PV = nRT

P = (n/V) RT

↓ ↓

π = CRT

where,
π = osmotic pressure,
C = molarity (mol/litre),
R = gas constant,
T = temperature (kelvin)

The unit for π is taken as atmospheric pressure. R = 0.082 litre atm/K mol.

Osmotic pressure liquid solutions class 12

ABNORMAL COLLIGATIVE PROPERTIES

The colligative properties of solution depend upon the number of solute particles present in solution. When the substance undergoes dissociation the number of particles increases and hence an increase in colligative property. In another case, the particles when associates, the number of particles decreases and a decrease in the colligative properties.

van’t Hoff Factor

Electrolytes dissociates or associates in aqueous solution and thus brings change in molality, molarity, mole fraction.

When some substance polymerises in solution, like acetic acid dimerises in benzene but dissociates in water give rise to abnormal concentration in contrast to as thought earlier.

So, there is change in colligative property and the ratio of observed colligative property with theoretical colligative property is known as Van’t Hoff factor ‘i’. The value of i > 1 for dissociation and i < 1 for association and extent of ‘i’ depends on the degree of dissociation or association.

In case of dissociation: For an electrolyte under dissociation and degree of dissociation α, we have

A_xB_y → xA^+y + yB^-x

Initially	After dissociation
A_xB_y	1	1 - α
xA^+y	0	xα
yB^-x	0	yα

Total number of moles of particle after dissociation = 1 - α + xα + yα
= 1 + α[x + y - 1]

Van’t Hoff factor,
i = ^{observed number of mole} / _{Theoretical value} = ^{1 + α[x + y - 1]} / ₁

In case of association: Suppose n moles of any substance polymerises.

nA → An

Initially	After association
nA	1	1 - α
An	0	α / n

Total number of mole after association = 1 + α (1/n - 1)

Observed colligative property = 1 - α + α/n

1 - α [1 - 1/n] / 1 = (n - αn - 1)/n = (n(1 - α) - 1)/n

So, i for association is < 1.

Van’t Hoff factor may be expressed in many forms

Azeotropes

Azeotropic mixtures or constant boiling mixtures are such mixtures whose liquid phase compositions are similar to that of vapour phase composition and due to this nature, they can not be separated by simple distillation.

To separate each component successfully a third component named entrainer is mixed which form heteroazeotrope with one of the component and having different boiling point (lower and higher) than previous azeotropes boiling point and thus make it easy to separate.

For example:

Water (weight – 4.5%, boiling point – 100^oC) and Ethyl alcohol (weight – 95.5%, boiling point – 78.5^oC) form low boiling point azeotrope (78.15^oC) if desired further separation to obtain pure ethyl alcohol, benzene is added (known as entrainer) to former azeotropic mixture and makes it hetero–azeotrope with alcohol having boiling point 67.8^oC. It then boils quickly than the remaining mixture and maximum of alcohol is separated further with benzene.

Azeotropic mixture with positive deviation (minimum boiling)

Components name		Composition by weight% of B	Boiling Point (K)		Azeotropic mixture
A	B		A	B
H₂O	C₂H₅OH	95.37	373	351	351.15
H₂O	C₃H₇OH	71.69	373	370	350.72
Acetone	CS₂	67	329.25	319.25	319.25
CHCl₃	C₂H₅OH	68.6	334.2	323	332.3

Azeotropic mixture with negative deviation (maximum boiling)

Components name	Composition by weight % of B		Boiling Point (K)
A	B		A	B	Azeotropic mixture
H₂O	HCl	20.3	373.0	188	383
H₂O	HI	57.0	373.0	239	400
H₂O	HNO₃	68.0	373.0	359	393.5
H₂O	HClO₄	71.6	373.0	383	476

Solved Examples

1. For an ideal binary liquid solutions with P_A⁰ > P_B⁰, which relation between X_A (mole fraction of A in liquid phase) and Y_A (mole fraction of A in vapour phase) is correct.

(A) X_A = Y_A

(B) X_A > Y_A

(D) X_A / X_B < Y_A / Y_B

Sol. (D).

∵ Y_A = (P_A⁰ / P_T) X_A
∴ Y_A/Y_B = (P_A⁰ / P_B⁰) × (X_A/X_B)
∴ P_A⁰ / P_B⁰ > 1 (given)
⇒ Y_A / Y_B > X_A / X_B

2. Dry air was passed successively through a solution of 5 g solute in 180 g of water and then through pure water. The loss in weight of solution was 2.50 g and that of pure solvent is 0.04 g. The molecular weight of the solute is

(A) 31.25

(B) 3.125

(D) None

Sol. (A).

P⁰ - P_s ∝ loss in weight of water chamber
P_s ∝ loss in weight of solution chamber
∴ (P⁰ - P_s)/P⁰ = n / N = w / m × W / M (for very dilute solution)

 0.04 / 2.54 = (5/m) / (180/18)
 ⇒ m = 31.25

3. The relationship between osmotic pressure at 273 K when 10 g glucose (P₁), 10 g urea (P₂) and 10 g sucrose (P₃) are dissolved in 250 ml of water is

P₁ > P₂ > P₃

P₃ > P₂ > P₁

P₂ > P₁ > P₃

P₂ > P₃ > P₁

Sol. (C).

Osmotic pressure is a colligative property and colligative property is directly proportional to concentration of solution.

In certain solvent, phenol dimerises to the extent of 60%. Its observed molecular mass in the solvent should be

> 94

< 94

= 94

unpredictable

Sol. (A).
i = Experimental colligative property / Theoretical colligative property

= 1 - α/2

= 1 - 0.6/2

= 0.7

i = Theoretical mol. mass / Observed mol. mass

Observed = 94 / 0.7

4. Assuming each salt to be 90% dissociated, which of the following will have highest osmotic pressure?

(A) decinormal Al₂(SO₄)₃

(B) decinormal BaCl₂

(D) a solution made by mixing equal volumes of (B) & (C)

Sol. (A).

The Vant Hoff factor is highest for Al₂(SO₄)₃ = 1 + (5 – 1) × 0.9 = 4.6

So, π = iCRT

5. Osmotic pressure of blood is 7.65 atm at 310 K. An aqueous solution of glucose that will be isotonic with blood is (wt./vol.)

(A) 5.41%

(B) 3.54%

(D) 53.4%

Sol. (A).

π_blood = 7.65 = C × (0.082) × 310

⇒ C = 7.65 / (310 × 0.082) = (mole/litre)

= 5.41%

Frequently Asked Questions

Solutions can exist in all three states of matter solid, liquid, and gas—depending on the physical state of the solvent. The state of the solvent determines the overall phase of the solution, while the solute can be in any phase (solid, liquid, or gas) before mixing.

1. Solid Solutions

A solid solution is a homogeneous mixture where the solvent is in the solid phase, and the solute may be solid, liquid, or gas. The solute particles are uniformly distributed within the solid’s crystal lattice.

Examples:

Alloys – Brass (zinc dissolved in copper), stainless steel (carbon and chromium dissolved in iron).
Doped semiconductors – Silicon infused with phosphorus atoms for electronics.
Applications: Metallurgy, electronics, and jewelry making.

2. Liquid Solutions

In a liquid solution, the solvent is a liquid, and the solute may be solid, liquid, or gas. These are the most common solutions encountered in daily life.

Examples:

Solid in liquid – Salt in water.
Liquid in liquid – Ethanol in water.
Gas in liquid – Carbon dioxide in soda.
Applications: Pharmaceuticals, beverages, cleaning agents, and industrial processes.

3. Gas Solutions

A gas solution has a gaseous solvent, and the solute can be a gas, liquid, or solid (though gases dissolving solids are rare under normal conditions).

Examples:

Air – A mixture of nitrogen (solvent), oxygen, carbon dioxide, and other gases.
Natural gas – Methane with small amounts of ethane, propane, and other gases.
Applications: Breathing air for humans and animals, industrial gas mixtures, refrigeration gases.

Key takeaway:
While many people associate solutions primarily with liquids, they exist across all states of matter. The underlying principle is homogeneity at the molecular level no matter the phase, the composition is uniform throughout.

S.no	Formulas List
1.	Liquid Solutions
2.	Electrochemistry
3.	Chemical Kinetics
4.	Ores and Metallurge
5.	P-Block Elements
6.	D-Block and Co-ordination Compounds
7.	Chemistry of Heavy Metals
8.	Alkyl and Aryl Halides
9.	Alcohol phenol and ether
10.	Aldehyde and Ketone

Liquid Solutions

Essentials to Identify or Rank Solvent in a Solution:

Concentration units and ways of expression

IDEAL SOLUTION

NON IDEAL SOLUTION

Solved Examples

Frequently Asked Questions

Related Links

Become one of thousands of satisfied students!

Frequently Asked Questions